2020-2021学年黑龙江省大庆市肇州县九年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省大庆市肇州县九年级(上)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1009.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 07:13:25 | ||
图片预览




文档简介
2020-2021学年黑龙江省大庆市肇州县九年级第一学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.若∠A的度数为30°,则tanA的值是( )
A. B. C. D.
2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
3.将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
4.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而减少,则x的取值范围是( )
A.x<1 B.x>1 C.x<﹣1 D.x>﹣1
5.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
6.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
7.如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A. B. C. D.
8.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA?OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
9.我国南方一些地区的农民戴的斗笠是圆锥形.已知圆锥的母线长为28cm,底面半径为24cm,要在斗笠的外表面刷上油漆,则刷漆部分的面积为( )
A.576cm2 B.576πcm2 C.672cm2 D.672πcm2
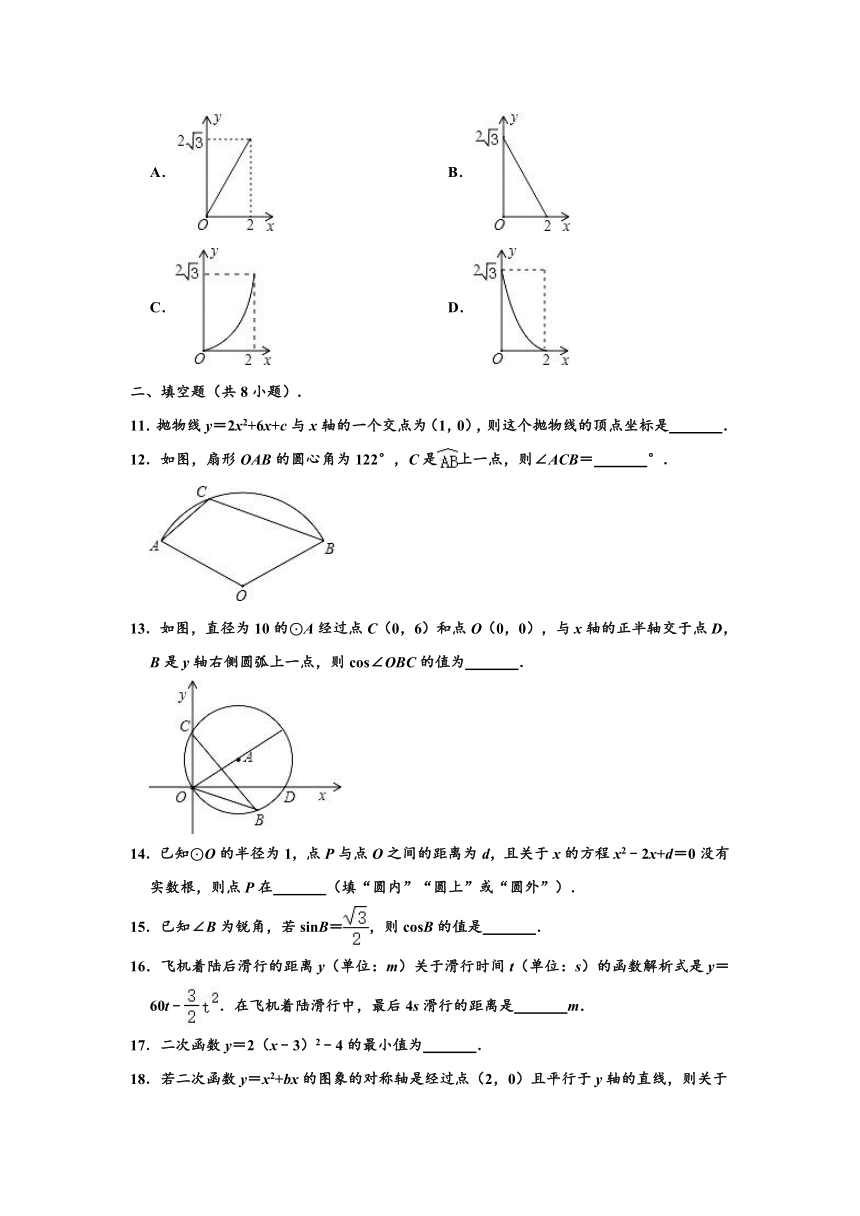
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
二、填空题(共8小题).
11.抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个抛物线的顶点坐标是 .
12.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= °.
13.如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
15.已知∠B为锐角,若sinB=,则cosB的值是 .
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣.在飞机着陆滑行中,最后4s滑行的距离是 m.
17.二次函数y=2(x﹣3)2﹣4的最小值为 .
18.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 .
三、解答题
19.计算:
(1)2sin30°一3tan45°?sin45°+4cos60°;
(2)+cos45°?sin60°.
20.如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
21.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
22.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD?AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
23.时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
参考答案
一、选择题(共10小题).
1.若∠A的度数为30°,则tanA的值是( )
A. B. C. D.
解:∵∠A的度数为30°,
∴tanA的值是:.
故选:D.
2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
解:∵y=(m+2)x|m|+2是y关于x的二次函数,
∴|m|=2且m+2≠0.
解得m=2.
故选:B.
3.将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
解:∵y=﹣3x2的顶点坐标为(0,0),y=﹣3(x﹣1)2﹣2的顶点坐标为(1,﹣2),
∴将抛物线y=﹣3x2向右平移1个单位,再向下平移2个单位,可得到抛物线y=﹣3(x﹣1)2﹣2.
故选:D.
4.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而减少,则x的取值范围是( )
A.x<1 B.x>1 C.x<﹣1 D.x>﹣1
解:y=﹣x2+2x+1=﹣(x﹣1)2+2,
抛物线的对称轴为直线x=1,
∵a=﹣1<0,
∴当x>1时,y随x的增大而减少.
故选:B.
5.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
解:当a<0时,二次函数顶点在y轴负半轴,一次函数经过一、二、四象限;
当a>0时,二次函数顶点在y轴正半轴,一次函数经过一、二、三象限.
故选:C.
6.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:C.
7.如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A. B. C. D.
解:∵AB是直径,
∴∠ADB=90°,
∵⊙O的半径是13,
∴AB=2×13=26,
由勾股定理得:AD=10,
∴sin∠B===,
∵∠ACD=∠B,
∴sin∠ACD=sin∠B=,
故选:D.
8.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA?OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,
而a<0,
∴<0,所以②错误;
∵C(0,c),OA=OC,
∴A(﹣c,0),
把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,
∴ac﹣b+1=0,所以③正确;
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,
∴x1?x2=,
∴OA?OB=﹣,所以④正确.
故选:B.
9.我国南方一些地区的农民戴的斗笠是圆锥形.已知圆锥的母线长为28cm,底面半径为24cm,要在斗笠的外表面刷上油漆,则刷漆部分的面积为( )
A.576cm2 B.576πcm2 C.672cm2 D.672πcm2
解:∵底面半径为24cm,底面周长=48π,
∴圆锥的侧面面积=×48π×28=672πcm2,故选D.
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
解:∵A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,
∴AO=2,OP=x,则AP=2﹣x,
∴tan60°==,
解得:AB=(2﹣x)=﹣x+2,
∴S△ABP=×PA×AB=(2﹣x)??(﹣x+2)=x2﹣2x+2,
故此函数为二次函数,
∵a=>0,
∴当x=﹣=2时,S取到最小值为:=0,
根据图象得出只有D符合要求.
故选:D.
二、填空题(每题3分,共24分)
11.抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个抛物线的顶点坐标是 (﹣,﹣) .
解:∵抛物线y=2x2+6x+c与x轴的一个交点为(1,0)
即抛物线经过点(1,0)
代入解析式得到c=﹣8
∴解析式是y=2x2+6x﹣8
∵y=ax2+bx+c的顶点坐标公式为(,)
代入公式求值得到顶点坐标是(,﹣)
故填空答案:(﹣,﹣).
12.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= 119 °.
解:如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣61°=119°.
故答案为:119.
13.如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
解:连接CD,
∵∠COD=90°,
∴CD是直径,
即CD=10,
∵点C(0,6),
∴OC=6,
∴OD==8,
∴cos∠ODC===,
∵∠OBC=∠ODC,
∴cos∠OBC=.
故答案为:.
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 圆外 (填“圆内”“圆上”或“圆外”).
解:∵方程x2﹣2x+d=0没有实数根,
∴△=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
15.已知∠B为锐角,若sinB=,则cosB的值是 .
解:∵∠B为锐角,且sinB=,
∴∠B=60°,
∴cosB=cos60°=,
故答案为:.
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣.在飞机着陆滑行中,最后4s滑行的距离是 24 m.
解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当t=16时,y=576,
所以600﹣576=24(米)
故答案是:24.
17.二次函数y=2(x﹣3)2﹣4的最小值为 ﹣4 .
解:二次函数y=2(x﹣3)2﹣4的开口向上,顶点坐标为(3,﹣4),
所以最小值为﹣4.
故答案为:﹣4.
18.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 x1=5,x2=﹣1 .
解:∵二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,
∴抛物线的对称轴为直线x=2,
则﹣=﹣=2,
解得:b=﹣4,
∴x2+bx=5即为x2﹣4x﹣5=0,
则(x﹣5)(x+1)=0,
解得:x1=5,x2=﹣1.
故答案为:x1=5,x2=﹣1.
三、解答题
19.计算:
(1)2sin30°一3tan45°?sin45°+4cos60°;
(2)+cos45°?sin60°.
解:(1)2sin30°一3tan45°?sin45°+4cos60°
=2×﹣3×1×+4×
=1﹣+2
=3﹣;
(2)+cos45°?sin60°
=+×
=+
=﹣+
=﹣.
20.如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
解:(1)∵二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
解得:h=1,a=﹣,
∴抛物线的对称轴为直线x=1;
(2)点A′是该函数图象的顶点.理由如下:
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,∠OA′B=30°,
∴OB=OA′=1,
∴A′B=OB=,
∴A′点的坐标为(1,),
∴点A′为抛物线y=﹣(x﹣1)2+的顶点.
21.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
【解答】证明(1)∵AB=CD,
∴=,即+=+,
∴=;
(2)由(1)知=,
∴AD=BC,
∵=,=,
∴∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
22.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD?AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
【解答】(1)证明:连接OC,
∵OA=OC,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥EF,
∵OC为半径,
∴EF是⊙O的切线.
(2)证明:连接BC,
∵AB为⊙O直径,AD⊥EF,
∴∠BCA=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ACB∽△ADC,
∴=,
∴AC2=AD?AB.
(3)解:∵∠ACD=30°,∠OCD=90°,
∴∠OCA=60°,
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=OC=2,∠AOC=60°,
∵在Rt△ACD中,AD=AC=×2=1,
由勾股定理得:DC=,
∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=×(2+1)×﹣=﹣π.
23.时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
解:(1)由题意可知:∠BAD=18°,
在Rt△ABD中,AB=18≈≈5.6(m),
答:应在地面上距点B约5.6m远的A处开始斜坡的施工;
(2)能,理由如下:
如图,过点C作CE⊥AD于点E,
则∠ECD=∠BAD=18°,
在Rt△CED中,CE=CD?cos18°≈2.8×0.95=2.66(m),
∵2.66>2.5,
∴能保证货车顺利进入地下停车场.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
解:(1)由题意,设抛物线的解析式为y=a(x﹣4)2﹣(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣=2
解得:a=
∴y=(x﹣4)2﹣
即:y=x2﹣x+2
当y=0时,x2﹣x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0);
(2)存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2,
∴AP+CP=BC=2
∴AP+CP的最小值为2;
(3)如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x=
∴D(,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D(,0)两点,
则
解得:
∴直线CE的解析式为y=﹣+2.
一、选择题(共10小题).
1.若∠A的度数为30°,则tanA的值是( )
A. B. C. D.
2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
3.将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
4.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而减少,则x的取值范围是( )
A.x<1 B.x>1 C.x<﹣1 D.x>﹣1
5.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
6.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
7.如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A. B. C. D.
8.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA?OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
9.我国南方一些地区的农民戴的斗笠是圆锥形.已知圆锥的母线长为28cm,底面半径为24cm,要在斗笠的外表面刷上油漆,则刷漆部分的面积为( )
A.576cm2 B.576πcm2 C.672cm2 D.672πcm2
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
二、填空题(共8小题).
11.抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个抛物线的顶点坐标是 .
12.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= °.
13.如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
15.已知∠B为锐角,若sinB=,则cosB的值是 .
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣.在飞机着陆滑行中,最后4s滑行的距离是 m.
17.二次函数y=2(x﹣3)2﹣4的最小值为 .
18.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 .
三、解答题
19.计算:
(1)2sin30°一3tan45°?sin45°+4cos60°;
(2)+cos45°?sin60°.
20.如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
21.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
22.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD?AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
23.时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
参考答案
一、选择题(共10小题).
1.若∠A的度数为30°,则tanA的值是( )
A. B. C. D.
解:∵∠A的度数为30°,
∴tanA的值是:.
故选:D.
2.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
解:∵y=(m+2)x|m|+2是y关于x的二次函数,
∴|m|=2且m+2≠0.
解得m=2.
故选:B.
3.将抛物线y=﹣3x2平移,得到抛物线y=﹣3(x﹣1)2﹣2,下列平移方式中,正确的是( )
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
解:∵y=﹣3x2的顶点坐标为(0,0),y=﹣3(x﹣1)2﹣2的顶点坐标为(1,﹣2),
∴将抛物线y=﹣3x2向右平移1个单位,再向下平移2个单位,可得到抛物线y=﹣3(x﹣1)2﹣2.
故选:D.
4.在二次函数y=﹣x2+2x+1的图象中,若y随x的增大而减少,则x的取值范围是( )
A.x<1 B.x>1 C.x<﹣1 D.x>﹣1
解:y=﹣x2+2x+1=﹣(x﹣1)2+2,
抛物线的对称轴为直线x=1,
∵a=﹣1<0,
∴当x>1时,y随x的增大而减少.
故选:B.
5.在同一坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( )
A. B.
C. D.
解:当a<0时,二次函数顶点在y轴负半轴,一次函数经过一、二、四象限;
当a>0时,二次函数顶点在y轴正半轴,一次函数经过一、二、三象限.
故选:C.
6.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:C.
7.如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A. B. C. D.
解:∵AB是直径,
∴∠ADB=90°,
∵⊙O的半径是13,
∴AB=2×13=26,
由勾股定理得:AD=10,
∴sin∠B===,
∵∠ACD=∠B,
∴sin∠ACD=sin∠B=,
故选:D.
8.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA?OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴在y轴的右侧,
∴b>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,
而a<0,
∴<0,所以②错误;
∵C(0,c),OA=OC,
∴A(﹣c,0),
把A(﹣c,0)代入y=ax2+bx+c得ac2﹣bc+c=0,
∴ac﹣b+1=0,所以③正确;
设A(x1,0),B(x2,0),
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,
∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,
∴x1?x2=,
∴OA?OB=﹣,所以④正确.
故选:B.
9.我国南方一些地区的农民戴的斗笠是圆锥形.已知圆锥的母线长为28cm,底面半径为24cm,要在斗笠的外表面刷上油漆,则刷漆部分的面积为( )
A.576cm2 B.576πcm2 C.672cm2 D.672πcm2
解:∵底面半径为24cm,底面周长=48π,
∴圆锥的侧面面积=×48π×28=672πcm2,故选D.
10.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. B.
C. D.
解:∵A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,
∴AO=2,OP=x,则AP=2﹣x,
∴tan60°==,
解得:AB=(2﹣x)=﹣x+2,
∴S△ABP=×PA×AB=(2﹣x)??(﹣x+2)=x2﹣2x+2,
故此函数为二次函数,
∵a=>0,
∴当x=﹣=2时,S取到最小值为:=0,
根据图象得出只有D符合要求.
故选:D.
二、填空题(每题3分,共24分)
11.抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个抛物线的顶点坐标是 (﹣,﹣) .
解:∵抛物线y=2x2+6x+c与x轴的一个交点为(1,0)
即抛物线经过点(1,0)
代入解析式得到c=﹣8
∴解析式是y=2x2+6x﹣8
∵y=ax2+bx+c的顶点坐标公式为(,)
代入公式求值得到顶点坐标是(,﹣)
故填空答案:(﹣,﹣).
12.如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB= 119 °.
解:如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣61°=119°.
故答案为:119.
13.如图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为 .
解:连接CD,
∵∠COD=90°,
∴CD是直径,
即CD=10,
∵点C(0,6),
∴OC=6,
∴OD==8,
∴cos∠ODC===,
∵∠OBC=∠ODC,
∴cos∠OBC=.
故答案为:.
14.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 圆外 (填“圆内”“圆上”或“圆外”).
解:∵方程x2﹣2x+d=0没有实数根,
∴△=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
15.已知∠B为锐角,若sinB=,则cosB的值是 .
解:∵∠B为锐角,且sinB=,
∴∠B=60°,
∴cosB=cos60°=,
故答案为:.
16.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣.在飞机着陆滑行中,最后4s滑行的距离是 24 m.
解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当t=16时,y=576,
所以600﹣576=24(米)
故答案是:24.
17.二次函数y=2(x﹣3)2﹣4的最小值为 ﹣4 .
解:二次函数y=2(x﹣3)2﹣4的开口向上,顶点坐标为(3,﹣4),
所以最小值为﹣4.
故答案为:﹣4.
18.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 x1=5,x2=﹣1 .
解:∵二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,
∴抛物线的对称轴为直线x=2,
则﹣=﹣=2,
解得:b=﹣4,
∴x2+bx=5即为x2﹣4x﹣5=0,
则(x﹣5)(x+1)=0,
解得:x1=5,x2=﹣1.
故答案为:x1=5,x2=﹣1.
三、解答题
19.计算:
(1)2sin30°一3tan45°?sin45°+4cos60°;
(2)+cos45°?sin60°.
解:(1)2sin30°一3tan45°?sin45°+4cos60°
=2×﹣3×1×+4×
=1﹣+2
=3﹣;
(2)+cos45°?sin60°
=+×
=+
=﹣+
=﹣.
20.如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
解:(1)∵二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
解得:h=1,a=﹣,
∴抛物线的对称轴为直线x=1;
(2)点A′是该函数图象的顶点.理由如下:
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,∠OA′B=30°,
∴OB=OA′=1,
∴A′B=OB=,
∴A′点的坐标为(1,),
∴点A′为抛物线y=﹣(x﹣1)2+的顶点.
21.如图,⊙O中,弦AB与CD相交于点E,AB=CD,连接AD、BC.
求证:(1)=;
(2)AE=CE.
【解答】证明(1)∵AB=CD,
∴=,即+=+,
∴=;
(2)由(1)知=,
∴AD=BC,
∵=,=,
∴∠ADE=∠CBE,∠DAE=∠BCE,
∴△ADE≌△CBE(ASA),
∴AE=CE.
22.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=AD?AB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
【解答】(1)证明:连接OC,
∵OA=OC,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥EF,
∵OC为半径,
∴EF是⊙O的切线.
(2)证明:连接BC,
∵AB为⊙O直径,AD⊥EF,
∴∠BCA=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ACB∽△ADC,
∴=,
∴AC2=AD?AB.
(3)解:∵∠ACD=30°,∠OCD=90°,
∴∠OCA=60°,
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=OC=2,∠AOC=60°,
∵在Rt△ACD中,AD=AC=×2=1,
由勾股定理得:DC=,
∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=×(2+1)×﹣=﹣π.
23.时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的倾斜角为18°,一楼到地下停车场地面的垂直高度CD=2.8m,一楼到地平线的距离BC=1m.
(1)为保证斜坡的倾斜角为18°,应在地面上距点B多远的A处开始斜坡的施工?(结果精确到0.1m)
(2)如果给该购物广场送货的货车高度为2.5m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
解:(1)由题意可知:∠BAD=18°,
在Rt△ABD中,AB=18≈≈5.6(m),
答:应在地面上距点B约5.6m远的A处开始斜坡的施工;
(2)能,理由如下:
如图,过点C作CE⊥AD于点E,
则∠ECD=∠BAD=18°,
在Rt△CED中,CE=CD?cos18°≈2.8×0.95=2.66(m),
∵2.66>2.5,
∴能保证货车顺利进入地下停车场.
24.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
解:(1)由题意,设抛物线的解析式为y=a(x﹣4)2﹣(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣=2
解得:a=
∴y=(x﹣4)2﹣
即:y=x2﹣x+2
当y=0时,x2﹣x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0);
(2)存在,
如图2,由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2,
∴AP+CP=BC=2
∴AP+CP的最小值为2;
(3)如图3,连接ME
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x=
∴D(,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D(,0)两点,
则
解得:
∴直线CE的解析式为y=﹣+2.
同课章节目录
