15.1.1同底数幂的乘法
图片预览



文档简介
(共17张PPT)
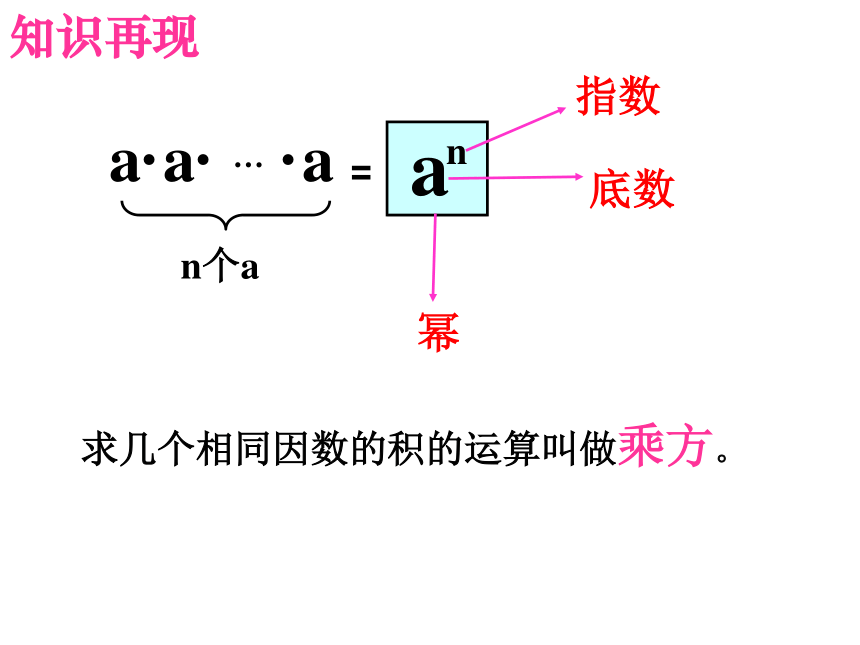
a
n
指数
幂
a·a· … ·a =
n个a
底数
求几个相同因数的积的运算叫做乘方。
知识再现
一种计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?
这是一种什么运算呢?
底数相同的
两个幂相乘
(根据乘方的意义)
(根据乘方的意义)
(根据乘法结合律)
你有什么发现?
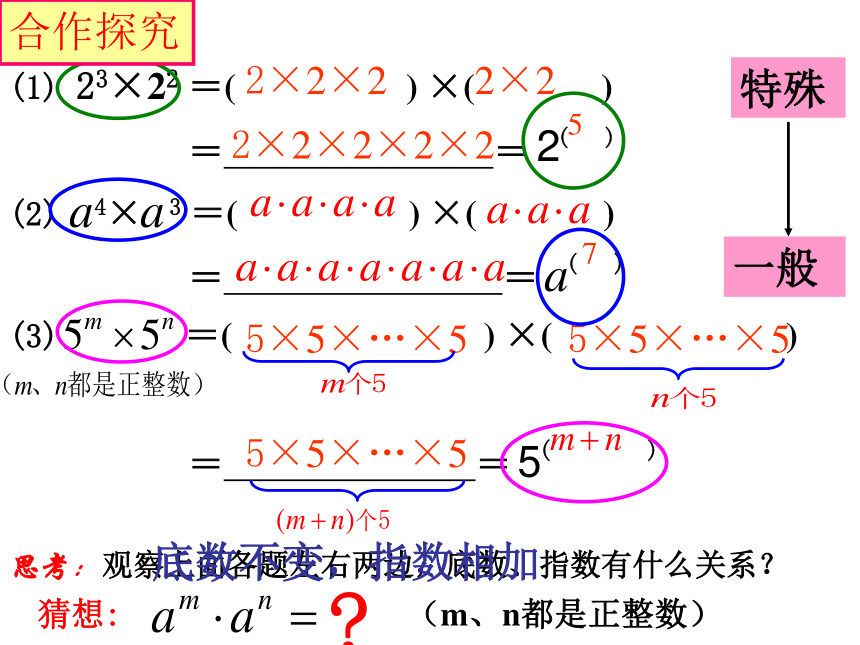
(1) 23×22 =( ) ×( )
= = ( )
2×2×2
2×2
2×2×2×2×2
5
(2) 4× 3 =( ) ×( )
= = ( )
7
5×5×…×5
5×5×…×5
(3) =( ) ×( )
= = ( )
5×5×…×5
思考:观察上面各题左右两边,底数、指数有什么关系?
猜想: (m、n都是正整数)
合作探究
特殊
一般
5
2
底数不变,指数相加
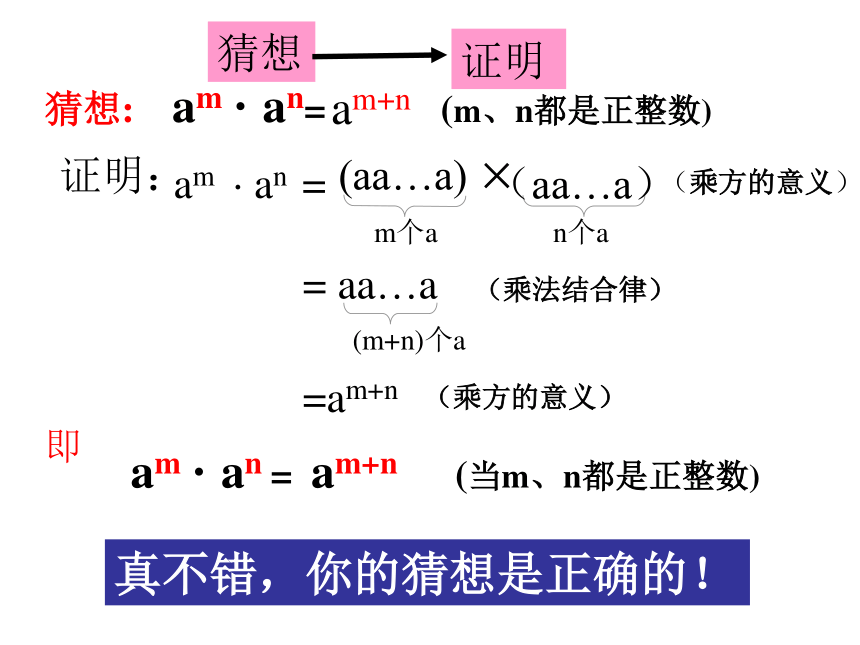
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a) ×
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
证明:
猜想
证明
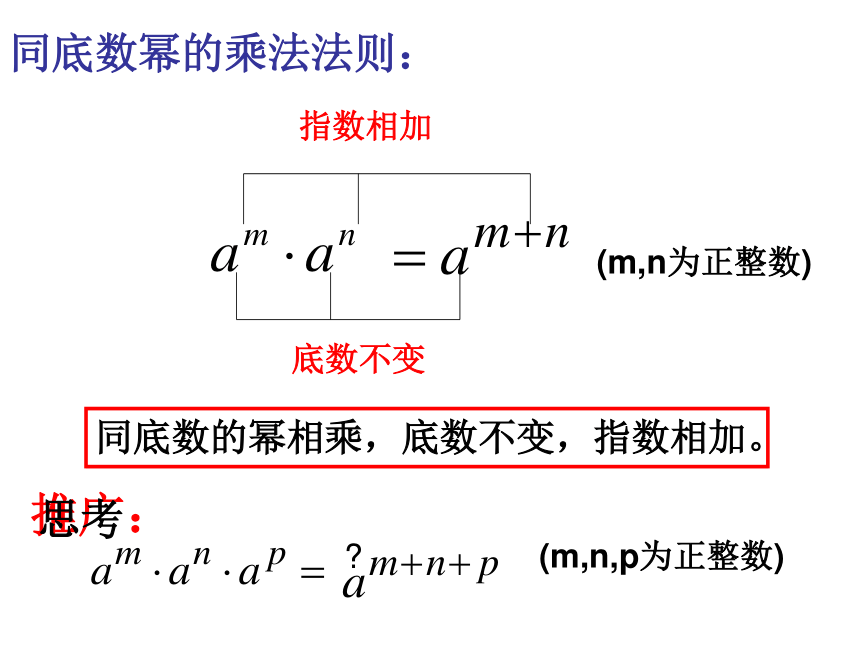
同底数的幂相乘,底数不变,指数相加。
底数不变
指数相加
同底数幂的乘法法则:
(m,n为正整数)
(m,n,p为正整数)
推广:
思考
(3)(-x ) 2 (-x ) 6
(1) 2 ×24 × 23
(4) (x+y)3 (x+y)4
(2)(-2 ) 8×(-2) 7
例1:计算下列各题:
=28
=(-2)15
= (-x ) 8
=(x+y)4
am · an=am+n
(m、n都是正整数)
公式中的a可表示一个数、字母、式子等.
学以致用
=-215
结果的底数化为正数
= x 8
下面的计算对不对?如果不对,怎样改正?
(1)b · b5= b5( )
(2)x2 ·x3 = x6 ( )
×
×
(3)b5 + b5 = b10 ( )
×
(4)a3+a4=a7 ( )
×
x2 ·x3 = x5
b5 + b5 = 2b5
b · b5= b6
计算下列各式子,唤醒你的记忆。
32
(-3)2
=9
=9
=27
33
(-3)3
= -27
(1)
(2)
34
(-3)4
=81
=81
32n (-3)2n
a2n (-a)2n
=
=
- 32n+1 (-3)2n+1
=
-a2n+1 (-a)2n+1
=
(1) 113 × (-11)6
(2) (-a)5× a× (-a)2
注意:
若底数互为相反数,先化为相同,
后运用法则
(3)(y-x)6 · (x-y)3
例2:计算下列各题:
能力提升
(a-b)2n=(b-a)2n
(a-b)2n+1= — (b-a)2n+1
计算:
(1) a3 · (-a)2
(3)(a-b)3 · (b-a)2
(2) -x5 ·(-x)5
选择题:
2、若xm =3, xn =2,则xm+n=( )
A. 5 B. 6 C. -5 D. -6
B
1、y2m+2 可写成( )
A. 2ym+1 B. ym · ym· y2 C.y2· ym+1 D.y2m+ y2
B
思维拓展训练
an+m=am·an
(m,n为正整数)
温馨提示:
若
,求
的值。
拓展提高
am · an = am+n
(m、n正整数)
我学到了什么?
知识
方 法
特殊 一般
说明:
在幂的运算中,经常会用到如下一些变形:
(1)(-a)2=a2,(-a)4=a4,(-a)6=a6……
(2)(-a)3= —a3,(-a)5= —a5,(-a)7=—a7……
(3)(b-a)2=(a-b)2,(b-a)4=(a-b)4……
(4)(b-a)3= —(a-b)3,(b-a)5= —(a-b)5……
a
n
指数
幂
a·a· … ·a =
n个a
底数
求几个相同因数的积的运算叫做乘方。
知识再现
一种计算机每秒可进行1014次运算,它工作103秒可进行多少次运算?
这是一种什么运算呢?
底数相同的
两个幂相乘
(根据乘方的意义)
(根据乘方的意义)
(根据乘法结合律)
你有什么发现?
(1) 23×22 =( ) ×( )
= = ( )
2×2×2
2×2
2×2×2×2×2
5
(2) 4× 3 =( ) ×( )
= = ( )
7
5×5×…×5
5×5×…×5
(3) =( ) ×( )
= = ( )
5×5×…×5
思考:观察上面各题左右两边,底数、指数有什么关系?
猜想: (m、n都是正整数)
合作探究
特殊
一般
5
2
底数不变,指数相加
猜想: am · an= (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a) ×
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
真不错,你的猜想是正确的!
证明:
猜想
证明
同底数的幂相乘,底数不变,指数相加。
底数不变
指数相加
同底数幂的乘法法则:
(m,n为正整数)
(m,n,p为正整数)
推广:
思考
(3)(-x ) 2 (-x ) 6
(1) 2 ×24 × 23
(4) (x+y)3 (x+y)4
(2)(-2 ) 8×(-2) 7
例1:计算下列各题:
=28
=(-2)15
= (-x ) 8
=(x+y)4
am · an=am+n
(m、n都是正整数)
公式中的a可表示一个数、字母、式子等.
学以致用
=-215
结果的底数化为正数
= x 8
下面的计算对不对?如果不对,怎样改正?
(1)b · b5= b5( )
(2)x2 ·x3 = x6 ( )
×
×
(3)b5 + b5 = b10 ( )
×
(4)a3+a4=a7 ( )
×
x2 ·x3 = x5
b5 + b5 = 2b5
b · b5= b6
计算下列各式子,唤醒你的记忆。
32
(-3)2
=9
=9
=27
33
(-3)3
= -27
(1)
(2)
34
(-3)4
=81
=81
32n (-3)2n
a2n (-a)2n
=
=
- 32n+1 (-3)2n+1
=
-a2n+1 (-a)2n+1
=
(1) 113 × (-11)6
(2) (-a)5× a× (-a)2
注意:
若底数互为相反数,先化为相同,
后运用法则
(3)(y-x)6 · (x-y)3
例2:计算下列各题:
能力提升
(a-b)2n=(b-a)2n
(a-b)2n+1= — (b-a)2n+1
计算:
(1) a3 · (-a)2
(3)(a-b)3 · (b-a)2
(2) -x5 ·(-x)5
选择题:
2、若xm =3, xn =2,则xm+n=( )
A. 5 B. 6 C. -5 D. -6
B
1、y2m+2 可写成( )
A. 2ym+1 B. ym · ym· y2 C.y2· ym+1 D.y2m+ y2
B
思维拓展训练
an+m=am·an
(m,n为正整数)
温馨提示:
若
,求
的值。
拓展提高
am · an = am+n
(m、n正整数)
我学到了什么?
知识
方 法
特殊 一般
说明:
在幂的运算中,经常会用到如下一些变形:
(1)(-a)2=a2,(-a)4=a4,(-a)6=a6……
(2)(-a)3= —a3,(-a)5= —a5,(-a)7=—a7……
(3)(b-a)2=(a-b)2,(b-a)4=(a-b)4……
(4)(b-a)3= —(a-b)3,(b-a)5= —(a-b)5……
