(公开课)15.1.1同底数幂的乘法
文档属性
| 名称 | (公开课)15.1.1同底数幂的乘法 |  | |
| 格式 | rar | ||
| 文件大小 | 983.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-04 20:54:17 | ||
图片预览






文档简介
(共43张PPT)
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们
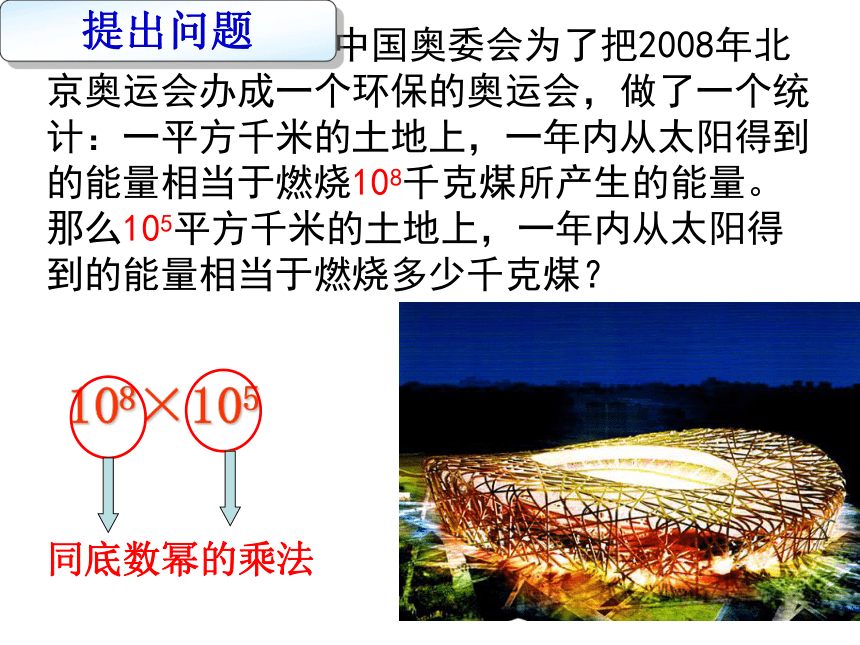
中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?
提出问题
108×105
同底数幂的乘法
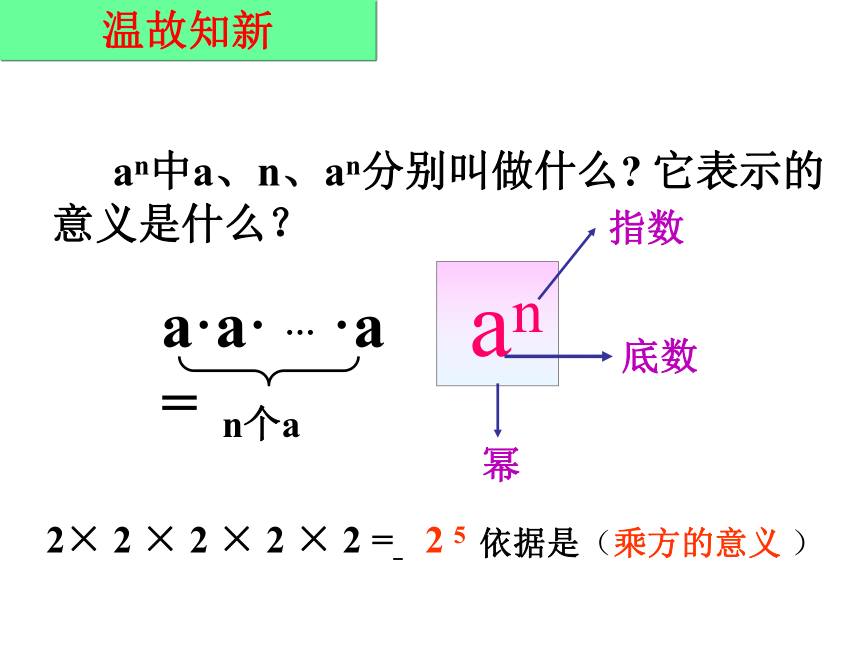
a·a· … ·a =
n个a
an中a、n、an分别叫做什么 它表示的意义是什么?
an
底数
幂
指数
温故知新
2× 2 × 2 × 2 × 2 =
依据是(乘方的意义 )
2 5
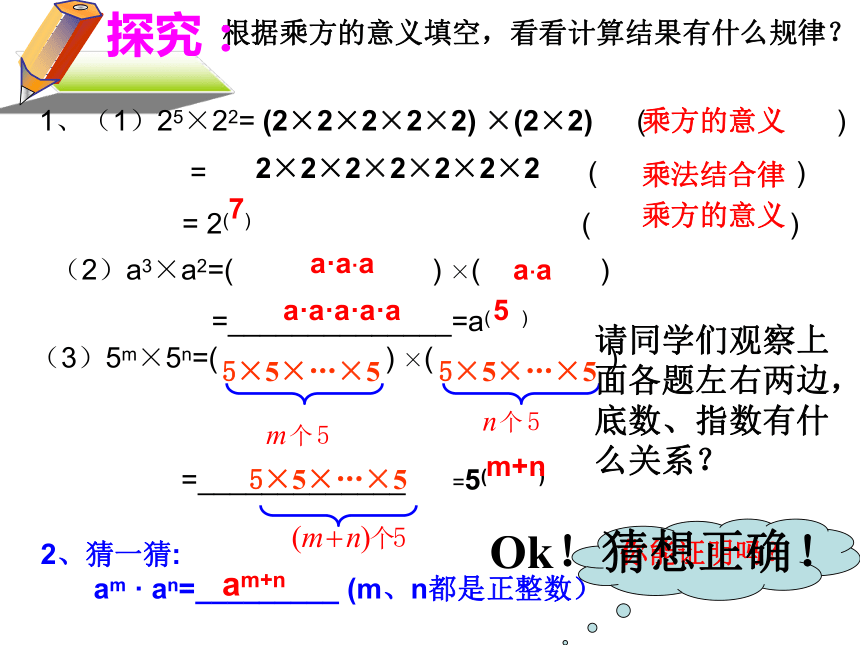
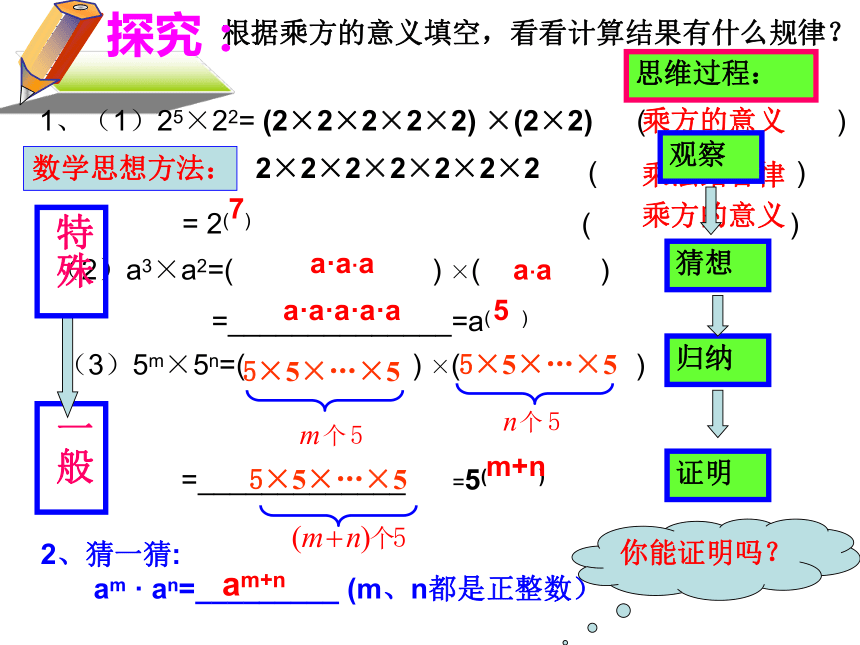
根据乘方的意义填空,看看计算结果有什么规律?
1、(1)25×22= ( )
= ( )
= 2( ) ( )
(2)a3×a2=( ) ×( )
=______________=a( )
(3)5m×5n=( ) ×( )
(2×2×2×2×2) ×(2×2)
2×2×2×2×2×2×2
7
乘方的意义
乘法结合律
乘方的意义
5
探究:
a·a·a
a·a
a·a·a·a·a
5×5×…×5
5×5×…×5
5×5×…×5
=_____________
=5( )
m+n
2、猜一猜:
am · an=_________ (m、n都是正整数)
am+n
你能证明吗?
请同学们观察上面各题左右两边,底数、指数有什么关系?
Ok!猜想正确!
猜想: am · an = (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
=
猜想
证明
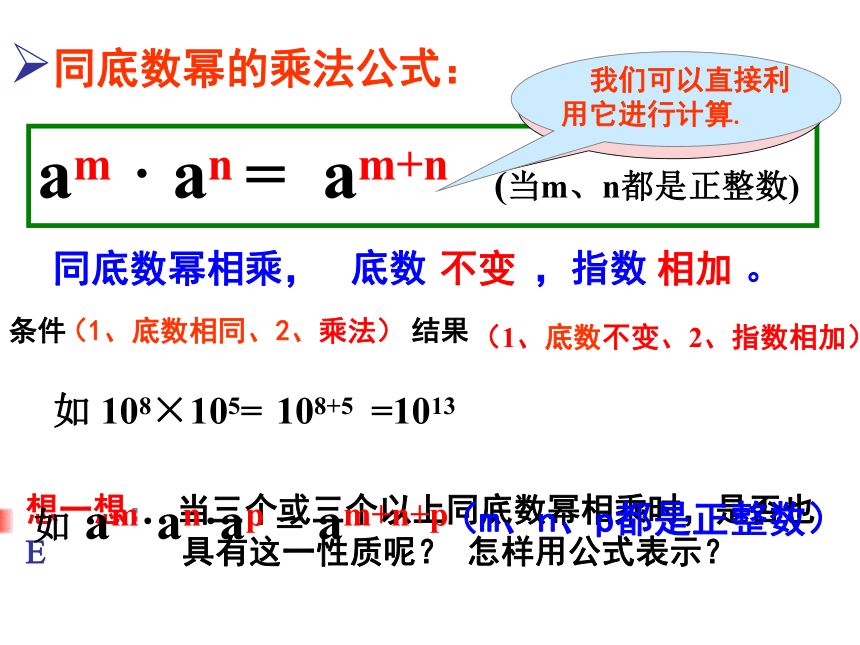
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 108×105=
108+5
=1013
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
条件
结果
(1、底数相同、2、乘法)
(1、底数不变、2、指数相加)
根据乘方的意义填空,看看计算结果有什么规律?
1、(1)25×22= ( )
= ( )
= 2( ) ( )
(2)a3×a2=( ) ×( )
=______________=a( )
(3)5m×5n=( ) ×( )
(2×2×2×2×2) ×(2×2)
2×2×2×2×2×2×2
7
乘方的意义
乘法结合律
乘方的意义
5
探究:
a·a·a
a·a
a·a·a·a·a
5×5×…×5
5×5×…×5
5×5×…×5
=_____________
=5( )
m+n
2、猜一猜:
am · an=_________ (m、n都是正整数)
am+n
你能证明吗?
一般
特殊
观察
猜想
归纳
证明
数学思想方法:
思维过程:
学以致用
( )2+3=( )5
2
5
2
5
103×104 =
(- 5) ·(- 5)7 =
( ) 3 ×( ) 2=
2
5
2
5
(-5)1+7=(-5)8
103+4 =107
a
a
a3+4
=58
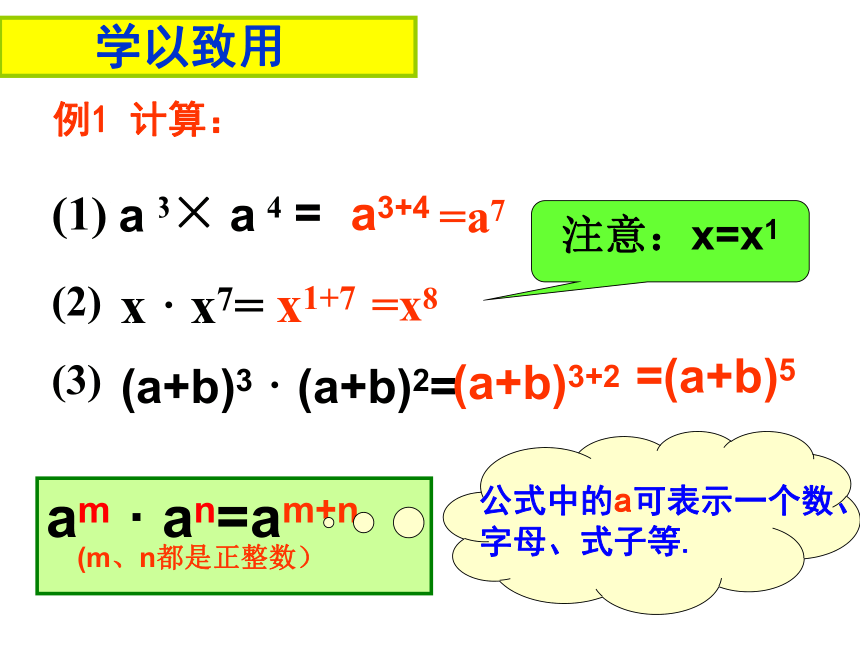
x · x7=
x1+7
(a+b)3 · (a+b)2=
(a+b)3+2
am · an=am+n
(m、n都是正整数)
公式中的a可表示一个数、字母、式子等.
例1 计算:
=a7
=x8
=(a+b)5
注意:x=x1
1. 105 × 106
2. a7 · a3
3. a6 · a6
xa · xb
(-3)3 × (-3)4
(-4)3 × (-4)5
xm-1 · xm+1
1011
a10
a12
xa+b
(-3)7=-37
(-4)8=48
x2m
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 +2y5 =3y5
c · c3 = c4
×
×
×
×
×
×
数学医院
注意 am · an 与 am + an的区别
﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.
注意 底数相同
注意 指数1不能忘
5. (x+y)3 · (-y-x)5
6.(a-b)3 · (b-a)2n
(a-b)2=(b-a)2
(a-b)3= — (b-a)3
(a-b)2n=(b-a)2n
(a-b)2n-1= — (b-a)2n-1
(n都为正整数)
同底数幂的乘法常用的几种恒等变形
例2.计算
登高望远
学以致用
光的速度约为3×105千米/秒,已知从太阳系外某颗恒星发出的光,经过15年到地球,一年以3×107秒计算,求这颗恒星与地球的距离。
解: 3×105× 3×107× 15
=(3×3×15)×(105×107)
=135×1012
=1.35×102×1012
=1.35×1014
答:这颗恒星与地球的距离是1.35×1014千米
挑战自我
ax+4=a6
X+4=6
2
2.解:2m+n
=2m×2n
=6×5
=30
3.解:∵ 3x+1=81×27
∴ 3x+1=34×33
∴ x+1=7
∴ x=6
6
30
逆用同底数幂乘法法则
方程思想
转化思想
同底数幂相乘,底数不变, 指数相加。
am · an = am+n (m、n正整数)
总结升华共提高
一、知识:
二、过程:
观察
猜想
归纳
证明
应用
三、思想方法:
特殊到一般思想
整体思想
转化思想
方程思想
例 若am+n=6,am=3,则an=
.
2
(1)若2a=3,则2a+3=______
(2)若5x+1=125,
求:①5x;
②(x-3)2008+x的值.
24
能力拓展
逆用同底数幂的乘法法则
计算下列各式:
A组
B组
C组
例1、 计算: (书P142)
1. x2 · x5
2. a · a6
解:x2 · x5 =
解:a · a6 =
x2+5=
x7
a1+6 =
a7
解:2 ×24 ×23 =
21+4+3 =
28
3. 2 ×24 ×23
例题讲解
注意:a=a1
4. xm · x3m+1
解: xm · x3m+1=
xm+3m+1=
x4m+1
变式: 2 ×(-2)4 ×(-2)3
变式:( x+y)m · (x+y)3m+1
1. b5 · b5 = 2b5
2. x4 · x4 = x16
3. c · c3 = c3
a2 + a2 = a4
m + m3 = m4
23 × 35 = 68
(-x)2 · (-x)3 = (-x)5 = -x5
× b10
× x8
√
× c4
×
×
× 2a2
1. b5 · b
2. 10 × 102 ×103
3. -a2 · a6
y2n · y2n+1
(-3)3 × (-3)4
(-4)3 × (-4)5
体验成功
练习:计算 (书P142)
练习一
1. 计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) -x5 ·(-x)5
(4) b5 · b
(1) 105×106
Good!
(-x8)
(5)-x2 · x6
2. 计算:
(1)x10 · x (2)10×102×104
(3) x5 ·x ·x3 (4)y4·y3·y2·y
解:
(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10
3.中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?
108 ×105
=1013 (千克)
(1) (-2)3×24
(2) (x+y)3 (y+x) 2
(3) (a-b)4(b-a) 3
例2.计算:
同底数幂相乘,底数必须相同.
例 若am+n=6,am=3,则an=
.
2
(1)若an=2,am=3, 则①am+3 , ②an+2
③am+n+3
(2)若5x+1=125,
求:①5x; ②(x-3)2008+x的值.
能力拓展
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )
能力挑战
m
x3
3
x2m
n
3
30
认真思考,我也行!
你的思维真灵活!
例3.已知:am=2,an=3.
求 am+n 的值.
解: am+n=am·an
=2×3
=6
思考:am+1,am+n+3呢?
拓展提高
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果用幂的形式表示)
15.2.1 同底数幂的乘法
49 ×77+6 ×74 ×75
=72 ×77+6 ×79
=79 +6 ×79
=7 ×79
=710
=1011
=a5
=x4m+1
= b6
(2)a2 ·a3
(3) xm x3m+1
(1)b5 · b
(1) 105×106
牛刀小试
1
y · y2 · y4
=y1+2+4
1
(2)
计算
(5)
练习
(-3)3×(-3)2
(3)y2n . yn+1
(4) - a2 ·a3
=(-3)5
=y3n+1
= -a5
am · an · ap =
am+n+p
(m、n、p都是正整数)
=105+6
=a2+3
=xm+3m+1
=y7
= b5+1
=-35
(4)(-3)2 . (-3)2
=(-3)2+2
=(-3)4
=34
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 +2y5 =3y5
c · c3 = c4
×
×
×
×
×
×
数学医院
注意 am · an 与 am + an的区别
﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.
注意 底数相同
注意 指数1不能忘
思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.
综合拓展
已知2x=3,2y=6,2z=12,试写出x,y,z的关系式.
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )
能力挑战
m
x3
3
x2m
n
3
30
认真思考,我也行!
你的思维真灵活!
例3.已知:am=2,an=3.
求 am+n 的值.
解: am+n=am·an
=2×3
=6
思考:am+1,am+n+3呢?
数学是创造性的艺术,
因为数学家创造了美好的新概念。
————哈尔莫斯
黄岩实验中学 李林华
拓展提高
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果用幂的形式表示)
15.2.1 同底数幂的乘法
49 ×77+6 ×74 ×75
=72 ×77+6 ×79
=79 +6 ×79
=7 ×79
=710
求下列式中的X值
32x-1=27×81
解:32x-1=33×34
∴32x-1=37
∴2x-1=7
∴x=4
1.主要学习了什么
同底数幂乘法法则: am · an = am + n
同底数幂相乘,底数不变,指数相加。
2. 理解、运用法则时要注意什么
(1)是否相乘
(2)底数是否相同(转化注意负号处理)
3.本节课用到哪些数学思想
特殊到一般到特殊、转化、整体等思想
(一条法则)
(两点注意)
(三种思想)
证明: am · an= (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,
底数 ,指数 。
不变
相加
思考:当三个或三个以上同底数幂相乘时,同底数幂的乘法公式是否也适用呢?怎样用公式表示?
am·an·ap =
am+n+p
(m、n、p都是正整数)
火眼金睛
1.下面的计算对不对?如果不对,怎样改正?
(1) a · a2= a2 ( ) (2 ) x2 ·y5 = xy7 ( )
(3) a +a2 = a3 ( ) (4)a3 · a3 = a9 ( )
(5)a3+a3 = a6 ( ) (6) a3 · a3 =a6 ( )
a · a2= a3
x2 · y5 = x2y5
a +a2 = a +a2
a3 · a3 =a6
a3+a3 = 2a3
×
×
×
×
√
×
你认为,用同底数幂相乘法则时应该注意些什么?
1.若am = 2,an = 3,
则am+n=___
2.已知: a2 · a6 = 28,
则a=___
a=2或-2
6
解:am+n=am·an=2×3=6
解:∵ a2·a6=a8=28
∴ a=±2
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
致我亲爱的同学们
中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?
提出问题
108×105
同底数幂的乘法
a·a· … ·a =
n个a
an中a、n、an分别叫做什么 它表示的意义是什么?
an
底数
幂
指数
温故知新
2× 2 × 2 × 2 × 2 =
依据是(乘方的意义 )
2 5
根据乘方的意义填空,看看计算结果有什么规律?
1、(1)25×22= ( )
= ( )
= 2( ) ( )
(2)a3×a2=( ) ×( )
=______________=a( )
(3)5m×5n=( ) ×( )
(2×2×2×2×2) ×(2×2)
2×2×2×2×2×2×2
7
乘方的意义
乘法结合律
乘方的意义
5
探究:
a·a·a
a·a
a·a·a·a·a
5×5×…×5
5×5×…×5
5×5×…×5
=_____________
=5( )
m+n
2、猜一猜:
am · an=_________ (m、n都是正整数)
am+n
你能证明吗?
请同学们观察上面各题左右两边,底数、指数有什么关系?
Ok!猜想正确!
猜想: am · an = (m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
=
猜想
证明
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?
底数 ,指数 。
不变
相加
同底数幂的乘法公式:
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
如 108×105=
108+5
=1013
如 am·an·ap =
am+n+p
(m、n、p都是正整数)
条件
结果
(1、底数相同、2、乘法)
(1、底数不变、2、指数相加)
根据乘方的意义填空,看看计算结果有什么规律?
1、(1)25×22= ( )
= ( )
= 2( ) ( )
(2)a3×a2=( ) ×( )
=______________=a( )
(3)5m×5n=( ) ×( )
(2×2×2×2×2) ×(2×2)
2×2×2×2×2×2×2
7
乘方的意义
乘法结合律
乘方的意义
5
探究:
a·a·a
a·a
a·a·a·a·a
5×5×…×5
5×5×…×5
5×5×…×5
=_____________
=5( )
m+n
2、猜一猜:
am · an=_________ (m、n都是正整数)
am+n
你能证明吗?
一般
特殊
观察
猜想
归纳
证明
数学思想方法:
思维过程:
学以致用
( )2+3=( )5
2
5
2
5
103×104 =
(- 5) ·(- 5)7 =
( ) 3 ×( ) 2=
2
5
2
5
(-5)1+7=(-5)8
103+4 =107
a
a
a3+4
=58
x · x7=
x1+7
(a+b)3 · (a+b)2=
(a+b)3+2
am · an=am+n
(m、n都是正整数)
公式中的a可表示一个数、字母、式子等.
例1 计算:
=a7
=x8
=(a+b)5
注意:x=x1
1. 105 × 106
2. a7 · a3
3. a6 · a6
xa · xb
(-3)3 × (-3)4
(-4)3 × (-4)5
xm-1 · xm+1
1011
a10
a12
xa+b
(-3)7=-37
(-4)8=48
x2m
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 +2y5 =3y5
c · c3 = c4
×
×
×
×
×
×
数学医院
注意 am · an 与 am + an的区别
﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.
注意 底数相同
注意 指数1不能忘
5. (x+y)3 · (-y-x)5
6.(a-b)3 · (b-a)2n
(a-b)2=(b-a)2
(a-b)3= — (b-a)3
(a-b)2n=(b-a)2n
(a-b)2n-1= — (b-a)2n-1
(n都为正整数)
同底数幂的乘法常用的几种恒等变形
例2.计算
登高望远
学以致用
光的速度约为3×105千米/秒,已知从太阳系外某颗恒星发出的光,经过15年到地球,一年以3×107秒计算,求这颗恒星与地球的距离。
解: 3×105× 3×107× 15
=(3×3×15)×(105×107)
=135×1012
=1.35×102×1012
=1.35×1014
答:这颗恒星与地球的距离是1.35×1014千米
挑战自我
ax+4=a6
X+4=6
2
2.解:2m+n
=2m×2n
=6×5
=30
3.解:∵ 3x+1=81×27
∴ 3x+1=34×33
∴ x+1=7
∴ x=6
6
30
逆用同底数幂乘法法则
方程思想
转化思想
同底数幂相乘,底数不变, 指数相加。
am · an = am+n (m、n正整数)
总结升华共提高
一、知识:
二、过程:
观察
猜想
归纳
证明
应用
三、思想方法:
特殊到一般思想
整体思想
转化思想
方程思想
例 若am+n=6,am=3,则an=
.
2
(1)若2a=3,则2a+3=______
(2)若5x+1=125,
求:①5x;
②(x-3)2008+x的值.
24
能力拓展
逆用同底数幂的乘法法则
计算下列各式:
A组
B组
C组
例1、 计算: (书P142)
1. x2 · x5
2. a · a6
解:x2 · x5 =
解:a · a6 =
x2+5=
x7
a1+6 =
a7
解:2 ×24 ×23 =
21+4+3 =
28
3. 2 ×24 ×23
例题讲解
注意:a=a1
4. xm · x3m+1
解: xm · x3m+1=
xm+3m+1=
x4m+1
变式: 2 ×(-2)4 ×(-2)3
变式:( x+y)m · (x+y)3m+1
1. b5 · b5 = 2b5
2. x4 · x4 = x16
3. c · c3 = c3
a2 + a2 = a4
m + m3 = m4
23 × 35 = 68
(-x)2 · (-x)3 = (-x)5 = -x5
× b10
× x8
√
× c4
×
×
× 2a2
1. b5 · b
2. 10 × 102 ×103
3. -a2 · a6
y2n · y2n+1
(-3)3 × (-3)4
(-4)3 × (-4)5
体验成功
练习:计算 (书P142)
练习一
1. 计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) -x5 ·(-x)5
(4) b5 · b
(1) 105×106
Good!
(-x8)
(5)-x2 · x6
2. 计算:
(1)x10 · x (2)10×102×104
(3) x5 ·x ·x3 (4)y4·y3·y2·y
解:
(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10
3.中国奥委会为了把2008年北京奥运会办成一个环保的奥运会,做了一个统计:一平方千米的土地上,一年内从太阳得到的能量相当于燃烧108千克煤所产生的能量。那么105平方千米的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤?
108 ×105
=1013 (千克)
(1) (-2)3×24
(2) (x+y)3 (y+x) 2
(3) (a-b)4(b-a) 3
例2.计算:
同底数幂相乘,底数必须相同.
例 若am+n=6,am=3,则an=
.
2
(1)若an=2,am=3, 则①am+3 , ②an+2
③am+n+3
(2)若5x+1=125,
求:①5x; ②(x-3)2008+x的值.
能力拓展
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )
能力挑战
m
x3
3
x2m
n
3
30
认真思考,我也行!
你的思维真灵活!
例3.已知:am=2,an=3.
求 am+n 的值.
解: am+n=am·an
=2×3
=6
思考:am+1,am+n+3呢?
拓展提高
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果用幂的形式表示)
15.2.1 同底数幂的乘法
49 ×77+6 ×74 ×75
=72 ×77+6 ×79
=79 +6 ×79
=7 ×79
=710
=1011
=a5
=x4m+1
= b6
(2)a2 ·a3
(3) xm x3m+1
(1)b5 · b
(1) 105×106
牛刀小试
1
y · y2 · y4
=y1+2+4
1
(2)
计算
(5)
练习
(-3)3×(-3)2
(3)y2n . yn+1
(4) - a2 ·a3
=(-3)5
=y3n+1
= -a5
am · an · ap =
am+n+p
(m、n、p都是正整数)
=105+6
=a2+3
=xm+3m+1
=y7
= b5+1
=-35
(4)(-3)2 . (-3)2
=(-3)2+2
=(-3)4
=34
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2) x5 ·x5 = x25 ( )
(3) b5 + b5 = b10 ( ) (4)y5 +2y5 = 3y10 ( )
﹒
(5) c · c3 = c3 ( ) (6) ﹙-2﹚3 · 24 = 27 ( )
b5 · b5= b10
b5 + b5 = 2b5
x5 · x5 = x10
y5 +2y5 =3y5
c · c3 = c4
×
×
×
×
×
×
数学医院
注意 am · an 与 am + an的区别
﹙-2﹚3﹒24 =-27
注意 同底数幂相乘,底数不变,指数相加.
注意 底数相同
注意 指数1不能忘
思维延伸
1已知xa=2,xb=3,求xa+b.
2已知x3·xa·x2a+1=x31,求a的值.
综合拓展
已知2x=3,2y=6,2z=12,试写出x,y,z的关系式.
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
填空:
(1)xm+n= x( )·x ( ) (2) x3 ·x4( )=x10
(3)27 × 37= 3( ) ×37
(4)xm ·( )=x3m
(5) 如果8=2x,那么 x= ( )
(6)若am=5,an=6,则am+n= ( )
能力挑战
m
x3
3
x2m
n
3
30
认真思考,我也行!
你的思维真灵活!
例3.已知:am=2,an=3.
求 am+n 的值.
解: am+n=am·an
=2×3
=6
思考:am+1,am+n+3呢?
数学是创造性的艺术,
因为数学家创造了美好的新概念。
————哈尔莫斯
黄岩实验中学 李林华
拓展提高
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
计算:(结果用幂的形式表示)
15.2.1 同底数幂的乘法
49 ×77+6 ×74 ×75
=72 ×77+6 ×79
=79 +6 ×79
=7 ×79
=710
求下列式中的X值
32x-1=27×81
解:32x-1=33×34
∴32x-1=37
∴2x-1=7
∴x=4
1.主要学习了什么
同底数幂乘法法则: am · an = am + n
同底数幂相乘,底数不变,指数相加。
2. 理解、运用法则时要注意什么
(1)是否相乘
(2)底数是否相同(转化注意负号处理)
3.本节课用到哪些数学思想
特殊到一般到特殊、转化、整体等思想
(一条法则)
(两点注意)
(三种思想)
证明: am · an= (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即:
am · an = am+n (当m、n都是正整数)
(aa…a)
(aa…a)
am+n
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,
底数 ,指数 。
不变
相加
思考:当三个或三个以上同底数幂相乘时,同底数幂的乘法公式是否也适用呢?怎样用公式表示?
am·an·ap =
am+n+p
(m、n、p都是正整数)
火眼金睛
1.下面的计算对不对?如果不对,怎样改正?
(1) a · a2= a2 ( ) (2 ) x2 ·y5 = xy7 ( )
(3) a +a2 = a3 ( ) (4)a3 · a3 = a9 ( )
(5)a3+a3 = a6 ( ) (6) a3 · a3 =a6 ( )
a · a2= a3
x2 · y5 = x2y5
a +a2 = a +a2
a3 · a3 =a6
a3+a3 = 2a3
×
×
×
×
√
×
你认为,用同底数幂相乘法则时应该注意些什么?
1.若am = 2,an = 3,
则am+n=___
2.已知: a2 · a6 = 28,
则a=___
a=2或-2
6
解:am+n=am·an=2×3=6
解:∵ a2·a6=a8=28
∴ a=±2
