四年级下册数学课件-第三单元《乘法运算定律》_青岛版 (共47张PPT)
文档属性
| 名称 | 四年级下册数学课件-第三单元《乘法运算定律》_青岛版 (共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 13:58:00 | ||
图片预览










文档简介
(共47张PPT)
近代最早设立植树节的地区是美国的内布拉斯加州。1872年4月10日,莫顿在该州园林协会举行的一次会议上,提出了设立植树节的建议。该州采纳了莫顿的建议,把4月10日定为该州的植树节,并于1932年发行世界上首枚植树节邮票,画面为两个儿童在植树。
四年级
数学环保课件
+
-
×
÷
+
-
×
÷
-
×
“植树节”是一些国家为激发人们爱林、造林的感情,促进国土绿化,保护人类赖以生存的生态环境,通过立法确定的节日。
1979年2月,中国五届人大常委会第六次会议决定。
植
树
节
一
共有25个小组,每组里4人负责挖坑、种树。
负责挖坑种树的一共有多少人?
25×4=100(人)
4×25=100(人)
我是这样计算的。
我这样算也可以。
一
共有25个小组,每组里4人负责挖坑、种树。负责挖坑种树的一共有多少人?
25×4=100(人)
4×25=100(人)
25×4
4×25
=
你能再举几个这样的例子吗?
观察下面每组的两个算式,它们有什么样的关系?
10×7
○
7×10
15×8
○
8×15
上面的每组算式有什么共同点?
从上面的算式,可以发现什么规律?
①每组算式中有两个因数,而且两个因数相同,只是交换了位置。
②每个等式中,左右两边的因数
的乘积相等。?
=
=
5×4=4×5
10×7=7×10
15×8=8×15
交换两个因数位置,积不变,这叫做乘法交换律。
如果用字母a、b表示两个因数,则可以写成:
a×b=b×a
a
·
b
=
b
·a
65×145=__×__
109×31=__×__
44×98=__×__
346×273=__×__
运用乘法交换律,
在__填上适当的数。
145
65
31
109
98
44
273
346
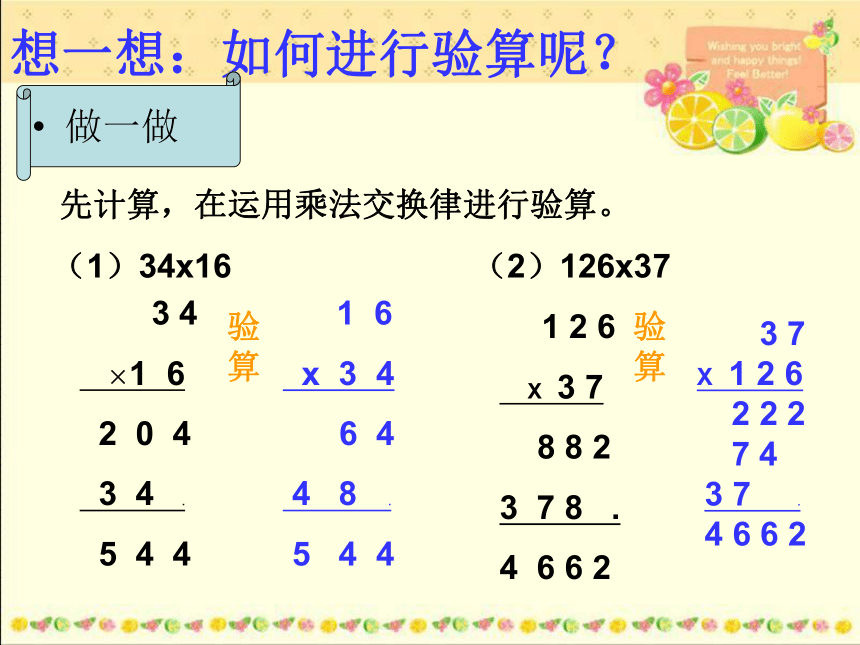
想一想:如何进行验算呢?
做一做
先计算,在运用乘法交换律进行验算。
3
4
×1
6
2
0
4
3
4
.
5
4
4
(1)34x16
(2)126x37
验算
1
6
x
3
4
6
4
4
8
.
5
4
4
1
2
6
X
3
7
8
8
2
3
7
8
.
4
6
6
2
验算
3
7
X
1
2
6
2
2
2
7
4
3
7
.
4
6
6
2
一共有25个小组,每组有2人负责抬水、浇树。
每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
我先计算一共种了多少棵树。
(25×5)×2
=125×2
=250(桶)
一共有25个小组,每组有2人负责抬水、浇树。
每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
我先计算每组植的树要浇多少桶水。
25×(5×2)
=25×10
=250(桶)
一共有25个小组,每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
(25×5)×2 25×(5×2)
=
这样的算式真有趣,怎么算结果都一样!你还能举些例子吗?
观察下面每组的两个算式,它们有什么样的关系?
(9×5)
×2
○
9×
(5×2)
6×
(25×4)
○
(6×25)
×4
上面的每组算式有什么共同点?
从上面的算式,可以发现什么规律?
①每组算式中有三个因数,而且三个
因数相同,只是计算时计算顺序不同。
②每个等式中,左右两边的因
数的乘积相等。?
=
=
(5×4)
×6=4×
(5×6)
(9×5)
×2=9×
(5×2)
(6×25)
×4=6×
(25×4)
三个数相乘,先乘前两个数,或者先乘后两个数,积不变。这叫做乘法结合律。
(a×b)
×c=a×
(b×c)
如果用字母表示则可以写成:
(a
·b)
·c=
a
·(b
·c)
这节课你学会了什么?
先填空,再想想应用了什么乘法运算定律。
45×16=16×
19×5×24=
×(5×
)
6×13×5=13×(
×
)
□
□
□
□
□
45
19
24
6
5
做一做
1、每瓶2元,买这些矿泉水,一共要花多少钱?
(5x24)x2
=120x2
=240
(元)
(24x2)x5
=48x5
=240
(元)
2、学校教学楼共有4层,每层有5间教室,每个教室安6盏灯。一共需要多少盏灯?
(5x6)x4
=30x4
=120
(盏)
(4x5)x6
=20x6
=120
(盏)
16×25×4怎样算比较简便?
16×25×4
=16×(25×4)
=16×100
=1600
想一想
用简便方法计算:
(1)
25x15x4
(2)
125x16
=(25x4)x15
=100x15
=1500
=(125x8)x2
=1000x2
=2000
+
-
×
÷
+
-
×
÷
-
×
方法一:先求出每队有多少人
方法二:先求出一共有多少组
四年级同学参加植树,把90人平均分成2队,每队平均分成5组,每组有多少人?
90÷2÷5
=45÷5
=9(人)
答:每组有9人。
90÷(2×5)
=90÷10
=9(人)
答:每组有9人。
哪种方法更简便呢?
观察下面每组的两个算式,
它们有什么样的关系?
90÷2÷5
○
90÷(2×5)
500÷
25÷4
○
500÷(25×4)
从上面的每组算式我们可以发现:
一个数连续除以两个数(0除外)等于
这个数除以这两个数的积
除法的运算性质
=
=
用字母可以表示为:
a÷b÷c=a÷(b×c)
(b、c
≠0)
a÷b÷c=a÷c÷b(b、c
≠
0)
a÷b×c=a÷(b÷c)
(b、c
≠0)
+
-
×
÷
+
-
×
÷
-
×
2、口算:
40x23x25
25x16
3、计算:
4x(5+8)
4x5+4x8
8x(4+5)
8x4+8x5
1、什么是乘法交换律?
什么是乘法结合律?
一共有25个小组,每组里4人负责挖坑、种树,有2人负责抬水、浇树。
一共有多少名同学参加了这次植树活动?
我先计算每组一共有多少人。
(4+2)×25
=6×25
=150(人)
我先分别计算挖坑、种树的和抬水、浇树的人数。
25×4+25×2
=100+50
=150(人)
一共有25个小组,每组里4人负责挖坑、种树,有2人负责抬水、浇树。
一共有多少名同学参加了这次植树活动?
(4+2)×25
4×25
=
25
×(4+2)
25×4
=
+2×25
+25×2
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
(4+2)×25
4×25+2×25
=
25
×(4+2)
25×4+25×2
=
(a+b)
×c=a×c+b×c
如果用字母a、b表示两个加数,
则可以写成:
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
a×(b+c)
=a×b+a×c
下面哪些算式运用了乘法分配律?
117×(3+7)
117×3+117×7
=
24×(5+12)
=
24×17
(4+5)
×
a
=
4
×
a
+5
×
a
=
36
×
(4×
6)
36
×
6×
4
下面每组算式的得数是否相等?如果相等,选择其中一个算出得数。
25×(200+4)
25×200+25×4
35×201
35×200+35
下面每组算式的得数是否相等?如果相等,选择其中一个算出得数。
265×(105-5)
265×105-265×5
25×11×4
11×(25×4)
乘法分配律的运用:
(1)(40+8)x
25
(2)
86x(100-2)
类型一
一定要括号外的数分别
乘括号里的两个数,
再把积相加或相减
=40x25+8x25
=1000+200
=1200
=86x100-86x2
=8600-172
=8428
(3)36x
34+36x66
(4)28x18-8x28
类型二
两个积中相同的
因数只能写一次
=36x(34+66)
=36x100
=3600
=28x(18-8)
=28x10
=280
(5)78x103
(6)125x81
类型三
把103看作100+3;
81看作80+1,
再用乘法分配律
=78x(100+3)
=78x100+78x3
=7800+234
=8034
=125x(80+1)
=125x80+125x1
=10000+125
=10125
(7)31x99
(8)42x98
类型四
把99看作100-1;
98看作100-2,
再用乘法分配律
=31x(100-1)
=31x100-31x1
=3100-31
=3059
=42x(100-2)
=42x100-42x2
=4200-84
=4116
(9)83+83x99
(10)125x81-125
类型五
把83看作83×1,
再用乘法分配律
=83x1+83x99
=83x(1+99)
=83x100
=8300
=125x81-125x1
=125x(81-1)
=125x80
=10000
我们来总结一下:
5×4=4×5
两个因数交换位置,积不变,这叫做乘法交换律。
a×b=b×a
如果用字母a、b表示两个因数,则可以写成:
我们来总结一下:
(5×4)
×6=4×
(5×6)
先把前两个数相乘,或者先把后两个数相乘,积不变。这叫做乘法结合律。
(a×b)
×c=a×
(b×c)
如果用字母a、b表示两个加数,
则可以写成:
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
(4+2)×25
4×25+2×25
=
(a+b)
×c=a×c+b×c
如果用字母a、b表示两个加数,
则可以写成:
a×(b+c)
=a×b+a×c
1、节约每一滴水
2、爱护花草树木
3、把垃圾分类处理
4、使用无磷洗衣粉
5、向周围的人宣传环保知识和其重要性,倡议人们保护环境
6、通过网络呼吁全世界的人们保护环境
……
环保宣言
①节约用电,自然光充足时关闭室内灯。离开教室时关
闭教室灯和走廊灯。
②节约用水,用水时尽量使用小水流,用完及时关闭水龙头。
③节约粮食,不剩饭,培养节俭品质。
④节约用纸,一张纸两面用,废纸放在回收箱中。
⑤爱护公物,门窗轻关轻开,桌椅轻搬轻放。
⑤爱护动植物,不折花、不攀树,不践踏绿地,不隔墙购物。
①不吸烟。
②做好卫生值日,保持环境卫生。
让我们共同努力,为子孙后代留下蓝天、碧水、绿地
近代最早设立植树节的地区是美国的内布拉斯加州。1872年4月10日,莫顿在该州园林协会举行的一次会议上,提出了设立植树节的建议。该州采纳了莫顿的建议,把4月10日定为该州的植树节,并于1932年发行世界上首枚植树节邮票,画面为两个儿童在植树。
四年级
数学环保课件
+
-
×
÷
+
-
×
÷
-
×
“植树节”是一些国家为激发人们爱林、造林的感情,促进国土绿化,保护人类赖以生存的生态环境,通过立法确定的节日。
1979年2月,中国五届人大常委会第六次会议决定。
植
树
节
一
共有25个小组,每组里4人负责挖坑、种树。
负责挖坑种树的一共有多少人?
25×4=100(人)
4×25=100(人)
我是这样计算的。
我这样算也可以。
一
共有25个小组,每组里4人负责挖坑、种树。负责挖坑种树的一共有多少人?
25×4=100(人)
4×25=100(人)
25×4
4×25
=
你能再举几个这样的例子吗?
观察下面每组的两个算式,它们有什么样的关系?
10×7
○
7×10
15×8
○
8×15
上面的每组算式有什么共同点?
从上面的算式,可以发现什么规律?
①每组算式中有两个因数,而且两个因数相同,只是交换了位置。
②每个等式中,左右两边的因数
的乘积相等。?
=
=
5×4=4×5
10×7=7×10
15×8=8×15
交换两个因数位置,积不变,这叫做乘法交换律。
如果用字母a、b表示两个因数,则可以写成:
a×b=b×a
a
·
b
=
b
·a
65×145=__×__
109×31=__×__
44×98=__×__
346×273=__×__
运用乘法交换律,
在__填上适当的数。
145
65
31
109
98
44
273
346
想一想:如何进行验算呢?
做一做
先计算,在运用乘法交换律进行验算。
3
4
×1
6
2
0
4
3
4
.
5
4
4
(1)34x16
(2)126x37
验算
1
6
x
3
4
6
4
4
8
.
5
4
4
1
2
6
X
3
7
8
8
2
3
7
8
.
4
6
6
2
验算
3
7
X
1
2
6
2
2
2
7
4
3
7
.
4
6
6
2
一共有25个小组,每组有2人负责抬水、浇树。
每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
我先计算一共种了多少棵树。
(25×5)×2
=125×2
=250(桶)
一共有25个小组,每组有2人负责抬水、浇树。
每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
我先计算每组植的树要浇多少桶水。
25×(5×2)
=25×10
=250(桶)
一共有25个小组,每组要种5棵树,每棵树要浇2桶水。
一共要浇多少桶水?
(25×5)×2 25×(5×2)
=
这样的算式真有趣,怎么算结果都一样!你还能举些例子吗?
观察下面每组的两个算式,它们有什么样的关系?
(9×5)
×2
○
9×
(5×2)
6×
(25×4)
○
(6×25)
×4
上面的每组算式有什么共同点?
从上面的算式,可以发现什么规律?
①每组算式中有三个因数,而且三个
因数相同,只是计算时计算顺序不同。
②每个等式中,左右两边的因
数的乘积相等。?
=
=
(5×4)
×6=4×
(5×6)
(9×5)
×2=9×
(5×2)
(6×25)
×4=6×
(25×4)
三个数相乘,先乘前两个数,或者先乘后两个数,积不变。这叫做乘法结合律。
(a×b)
×c=a×
(b×c)
如果用字母表示则可以写成:
(a
·b)
·c=
a
·(b
·c)
这节课你学会了什么?
先填空,再想想应用了什么乘法运算定律。
45×16=16×
19×5×24=
×(5×
)
6×13×5=13×(
×
)
□
□
□
□
□
45
19
24
6
5
做一做
1、每瓶2元,买这些矿泉水,一共要花多少钱?
(5x24)x2
=120x2
=240
(元)
(24x2)x5
=48x5
=240
(元)
2、学校教学楼共有4层,每层有5间教室,每个教室安6盏灯。一共需要多少盏灯?
(5x6)x4
=30x4
=120
(盏)
(4x5)x6
=20x6
=120
(盏)
16×25×4怎样算比较简便?
16×25×4
=16×(25×4)
=16×100
=1600
想一想
用简便方法计算:
(1)
25x15x4
(2)
125x16
=(25x4)x15
=100x15
=1500
=(125x8)x2
=1000x2
=2000
+
-
×
÷
+
-
×
÷
-
×
方法一:先求出每队有多少人
方法二:先求出一共有多少组
四年级同学参加植树,把90人平均分成2队,每队平均分成5组,每组有多少人?
90÷2÷5
=45÷5
=9(人)
答:每组有9人。
90÷(2×5)
=90÷10
=9(人)
答:每组有9人。
哪种方法更简便呢?
观察下面每组的两个算式,
它们有什么样的关系?
90÷2÷5
○
90÷(2×5)
500÷
25÷4
○
500÷(25×4)
从上面的每组算式我们可以发现:
一个数连续除以两个数(0除外)等于
这个数除以这两个数的积
除法的运算性质
=
=
用字母可以表示为:
a÷b÷c=a÷(b×c)
(b、c
≠0)
a÷b÷c=a÷c÷b(b、c
≠
0)
a÷b×c=a÷(b÷c)
(b、c
≠0)
+
-
×
÷
+
-
×
÷
-
×
2、口算:
40x23x25
25x16
3、计算:
4x(5+8)
4x5+4x8
8x(4+5)
8x4+8x5
1、什么是乘法交换律?
什么是乘法结合律?
一共有25个小组,每组里4人负责挖坑、种树,有2人负责抬水、浇树。
一共有多少名同学参加了这次植树活动?
我先计算每组一共有多少人。
(4+2)×25
=6×25
=150(人)
我先分别计算挖坑、种树的和抬水、浇树的人数。
25×4+25×2
=100+50
=150(人)
一共有25个小组,每组里4人负责挖坑、种树,有2人负责抬水、浇树。
一共有多少名同学参加了这次植树活动?
(4+2)×25
4×25
=
25
×(4+2)
25×4
=
+2×25
+25×2
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
(4+2)×25
4×25+2×25
=
25
×(4+2)
25×4+25×2
=
(a+b)
×c=a×c+b×c
如果用字母a、b表示两个加数,
则可以写成:
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
a×(b+c)
=a×b+a×c
下面哪些算式运用了乘法分配律?
117×(3+7)
117×3+117×7
=
24×(5+12)
=
24×17
(4+5)
×
a
=
4
×
a
+5
×
a
=
36
×
(4×
6)
36
×
6×
4
下面每组算式的得数是否相等?如果相等,选择其中一个算出得数。
25×(200+4)
25×200+25×4
35×201
35×200+35
下面每组算式的得数是否相等?如果相等,选择其中一个算出得数。
265×(105-5)
265×105-265×5
25×11×4
11×(25×4)
乘法分配律的运用:
(1)(40+8)x
25
(2)
86x(100-2)
类型一
一定要括号外的数分别
乘括号里的两个数,
再把积相加或相减
=40x25+8x25
=1000+200
=1200
=86x100-86x2
=8600-172
=8428
(3)36x
34+36x66
(4)28x18-8x28
类型二
两个积中相同的
因数只能写一次
=36x(34+66)
=36x100
=3600
=28x(18-8)
=28x10
=280
(5)78x103
(6)125x81
类型三
把103看作100+3;
81看作80+1,
再用乘法分配律
=78x(100+3)
=78x100+78x3
=7800+234
=8034
=125x(80+1)
=125x80+125x1
=10000+125
=10125
(7)31x99
(8)42x98
类型四
把99看作100-1;
98看作100-2,
再用乘法分配律
=31x(100-1)
=31x100-31x1
=3100-31
=3059
=42x(100-2)
=42x100-42x2
=4200-84
=4116
(9)83+83x99
(10)125x81-125
类型五
把83看作83×1,
再用乘法分配律
=83x1+83x99
=83x(1+99)
=83x100
=8300
=125x81-125x1
=125x(81-1)
=125x80
=10000
我们来总结一下:
5×4=4×5
两个因数交换位置,积不变,这叫做乘法交换律。
a×b=b×a
如果用字母a、b表示两个因数,则可以写成:
我们来总结一下:
(5×4)
×6=4×
(5×6)
先把前两个数相乘,或者先把后两个数相乘,积不变。这叫做乘法结合律。
(a×b)
×c=a×
(b×c)
如果用字母a、b表示两个加数,
则可以写成:
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这叫做乘法分配律。
(4+2)×25
4×25+2×25
=
(a+b)
×c=a×c+b×c
如果用字母a、b表示两个加数,
则可以写成:
a×(b+c)
=a×b+a×c
1、节约每一滴水
2、爱护花草树木
3、把垃圾分类处理
4、使用无磷洗衣粉
5、向周围的人宣传环保知识和其重要性,倡议人们保护环境
6、通过网络呼吁全世界的人们保护环境
……
环保宣言
①节约用电,自然光充足时关闭室内灯。离开教室时关
闭教室灯和走廊灯。
②节约用水,用水时尽量使用小水流,用完及时关闭水龙头。
③节约粮食,不剩饭,培养节俭品质。
④节约用纸,一张纸两面用,废纸放在回收箱中。
⑤爱护公物,门窗轻关轻开,桌椅轻搬轻放。
⑤爱护动植物,不折花、不攀树,不践踏绿地,不隔墙购物。
①不吸烟。
②做好卫生值日,保持环境卫生。
让我们共同努力,为子孙后代留下蓝天、碧水、绿地
