第2章复习课

(共47张PPT)
有理数这一章都学完了，今天我们该做什么了？
第二章 有理数及其运算
——复习课
学习目标：
1.在具体情境中理解有理数及其运算意义;
2.会比较有理数的大小，会求相反数、绝对值、倒数，掌握五则运算及混合运算，正确使用运算律；
3.能运用有理数及其运算解决实际问题。
有理数
有关概念
正数、负数
相反数
数轴
绝对值
倒数
比较有理数的大小
正有理数
0
负有理数
正整数
正分数
负整数
负分数
运算
加法
减法
乘法
除法
乘方
交换律：加法、乘法
结合律：加法、乘法
分配律：乘法对加法的
解决实际问题
混合运算顺序
例　1、把各数分别填在相应的集合里。
8、-16/8、-1、-8、-（-1/8）、0。
整数集合 （ ）
分数集合 （ ）
正数集合 （ ）
负数集合 （ ）
正整数集合（ ）
有理数集合 （ ）
8， -16/8，-1，-8， 0 …
-（-1/8） …
8， -（-1/8） …
-16/8， -1，-8 …
8 …
8，-16/8，-1，-8，-（-1/8），0 …
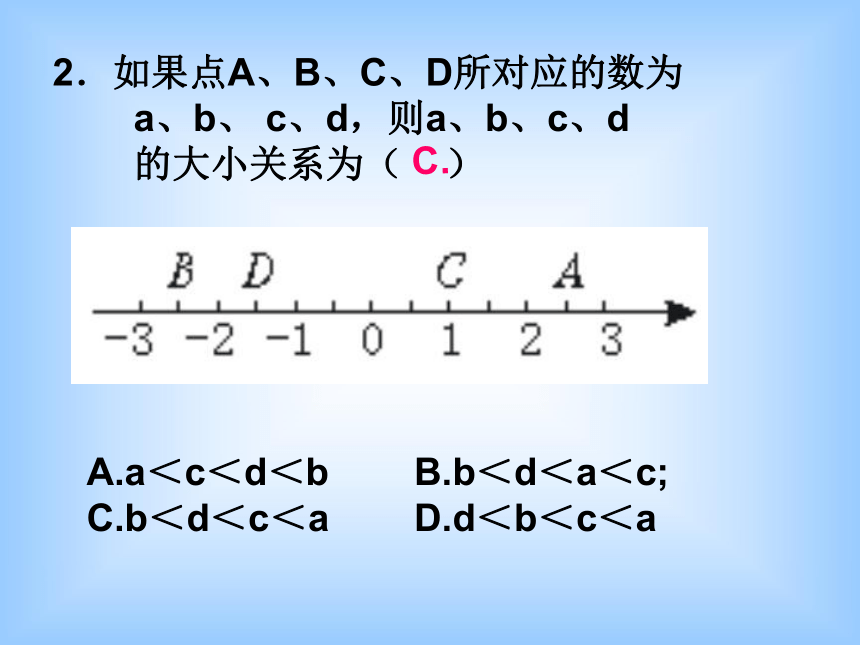
2．如果点A、B、C、D所对应的数为
　 a、b、 c、d，则a、b、c、d
　的大小关系为（ ）
A.a＜c＜d＜b B.b＜d＜a＜c;
C.b＜d＜c＜a D.d＜b＜c＜a
C.
⑴符号相反的两个数，必互为相反数 ( )
⑵数a 的相反数在数轴上对应的点，一定在原点左侧( )
⑶数轴上，离原点越远的点对应的数就越大 （ ）
⑷几个有理数相乘，负因数个数为奇数时，则积为负数 ( )
⑸－16÷ ×（－3）＝－16÷（－1）＝16 ( )
⑹ 若 a + b < 0 且 ab < 0, 则 a < 0 , b < 0 （ ）
？
牛刀小试 ：
×
×
×
×
×
×
结.
判断题
2.___ 的倒数是它本身,________的绝对值是它本身.平方等于它本身的数是 ，立方等于它本身的数是 。
3. a+b=0,则a与b＿＿＿＿＿＿＿＿　　.
4.最大的负整数与绝对值最小的数的和是____
5. 若b＜0且a=|b|，则a与b的关系是______.
1.
±1
正数和零
互为相反数
－１
互为相反数
0和1
0和±1
6.某人向东走了4千米记作+4千米，那么－2
千米表示＿＿＿＿＿＿＿＿＿？
7. 如果－|a| = |a|，那么a ＿＿＿＿＿.
向西走了２千米
＝０
8．如果▲表示最小的正整数， ●表示最大的负整数， ■表示绝对值最小的有理数，那么（▲ ＋ ● ）× ■ ＝ 。
0
9.已知 |a| + |b| +|c| = 0,
则 a = ____, b = _____, c = ____.
10.在数轴上与表示-1的点相距4个单位长度
的点表示的数是＿＿＿＿＿。
11. 在数轴上距离原点为2的点所对应的数为＿＿＿＿＿＿＿，它们互为＿＿＿＿.
0
0
0
-6 -5 -4 -3 -2 -1 0 1 2 3 4
－５和３
±2
相反数
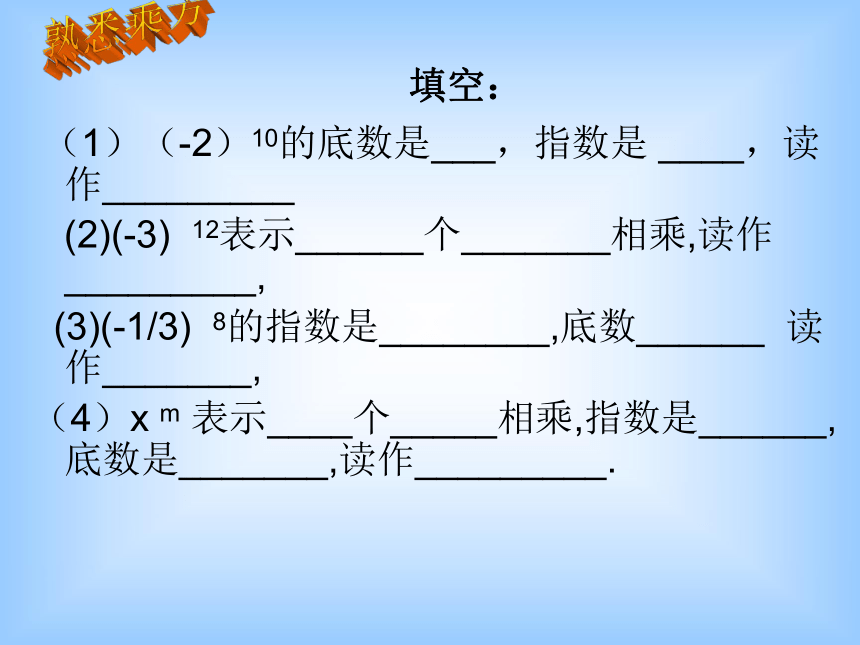
填空：
（1）（-2）10的底数是___，指数是 ____，读作_________
(2)(-3) 12表示______个_______相乘,读作_________,
(3)(-1/3) 8的指数是________,底数______ 读作_______,
（4）x m 表示____个_____相乘,指数是______,底数是_______,读作_________.
1.若|x|－|y|=0，则（ ）
A.x=y B.x=－y
C.x=y=0 D.x=y或x=－y
2.有理数a,b在数轴上对应位置如图所示，
则a+b的值为（ ）
A.大于0 B.小于0
C.等于0 D.大于a
D
B.
　A.负数 　　B.正数
C.非正数　　D.非负数
4 .|x|=1,则x与－3的差为（ ）
A. 4 B. －2
C. 4或2　　　D. 2
C
C.
|x|=1，∴ x＝±１
１－（－３）＝４
－１－（－３）
＝－１＋＝２
∴选C.
5.下列说法中，正确的是（ ）
A. 一个有理数的绝对值不小于它自身;
B. 若两个有理数的绝对值相等，
则这两个数相等.
C. 若两个有理数的绝对值相等，
则这两个数互为相反数;
D. －a的绝对值等于a
A
6.下列说法中，正确的是( )
(A). 0是最小的有理数
(B). 0 是最小整数
(C) .0的倒数和相反数都是0
(D) .0是最小的非负数
7.下列结论正确的是（ ）
A.若|x|=|y|，则x=－y
B.若x=－y，则|x|=|y|
C.若|a|＜|b|，则a＜b
D.若a＜b，则|a|＜|b|
负数更小！
零无倒数！
D
×
X=2,y=－2,满足X=－y,|x|=2,|y|=2,
所以|x|=|y|
选B.
B
8.下列计算正确的是( )
D
三．1.写出大于－4.1且小于2.5的所有整数，
　　 数并把它们在数轴上表示出来.
大于－4.1且小于2.5的所有整数为
　　-4.-3.-2.-1.0.1.2.
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
2、已知|a|=5,|b|=2, ab<0.
求：1. 3a+2b的值; 2. ab的值.
解：1.∵|a|=5,∴a=_______
∵|b|=2,∴b=_______
∵ab<0,∴当a=____时，b=__,
当a=_____时，b＝_______.
∴3a+2b=_______或3a+2b=_______.
2.ab=_______
∴3a+2b的值为_______，ab的值为
_______.
±5
±2
5
-2
-5
2
11
-11
-10
11或-11
-10
在有理数运算中，有时利用运算律可以简化计算．
如：13+（－12）+17+（－18）
=（13+17）+[（－12）+（－18）]
=30+（－30）
=0
加法交换律,
结合律
乘法交换律,结合律
有理数的加法运算律和乘法运算律与小学学过的运算律相同．当符号确定之后，就归结为小学学过的加减运算和乘除运算
有理数的运算律为：加法的交换律、加法结合律、乘法的交换律、乘法结合律，乘法对加法的分配律．
计算：（1）11+（－22）－3×（－11）
解：（1）11+（－22）－3×（－11）
=11+(－22) –( - 33 )
=11+（－22）+33
=22
先乘除,后加减
注意符号！
解.
注意符号！
注意符号！
先算括号里面的！
4、若（x-1)2+|y+4|=0,则3x+5y=______
∵X-1=0,y+4=0, ∴x=1 ,y=-4
∴3x+5y=3×1+5×(-4)=3-20=-17
5、若|a-3|+ |3a-4b|=0,则-2a+8b=____
6、| 7 |=（　　），|- 7 |=（　　）
绝对值是7的数是（　　）
7、若|3- |+|4- |=_______
±７
７
７
1
非负数性质的应用
数形结合的思想方法
已知︱a︱>︱b︱,且ａ<0,b>0,试比
较a,b,-a,-b的大小
分类讨论的思想
比较1＋a与1－a的大小。
练习
1、已知有理数a、b、c在数轴上的位置如图，化简|a|-|a+b|+|c-a|+|b+c||
b
a
0
c
有理数的应用
1、某公交车上原有乘客22人，经过4个站点时上下车情况如下（上车为正、下车为负）（－6,+3），（－5,+4），（－3,+1），（－4,+1），问此时车上还有多少乘客
2、市话费在3分钟内一次计费0.22元，超过3分钟的每分钟0.11元，小华一次打了12分钟，问这次通话费多少元？
张大爷家今年收获了10口袋谷子，准备出售，称得质量如下：（单位：公斤）
182、 177、182.5、 181 、 180 、
178 、183 、177.5、 184 、 185
试问这10袋谷子的总质量是多少？
方法对对碰 ：
结.
如果每公斤谷子可卖1元，
则张大爷能得到多少钱？
下表列出了国外几个城市与北京的时差
（带正号的数表示同一时刻比北京时间早
的 时数）
（1）如果现在的北京时间是7：00，那么现在的纽约时间是多少？
（2）小明现在想给远在巴黎的姑妈打电话，你认为合适吗？
城　市 时差/时
纽　约 －13
巴　黎 －7
东　京 +1
芝加哥 －14
解.(1) -13+7=-6 (2)-7+7=0
答.(1)昨天18点. (2) 不适合.
在学习了这一章后，不仅要把内容解、掌握了，还要能体会一些重要的思想方法：如数轴、相反数、绝对值、有理数大小比较．有理数的运算法则及运算律的研究都离不开观察、探究，即观察——探究法；如在研究相反数、绝对值、有理数的加法法则、乘法法则、乘方运算的符号法则等，都是按有理数分为正数、负数、0三类分别研究的，
即：分类思想；还有：数形结合想，用数轴上的点来表示有理数，就是最简单的数形结合思想的体现．结合数轴表示有理数，对于理解有理数的绝对值、相反数等概念以及有理数大小的比较等，更具有直观性．另外，在运算中，要注意符号、运算顺序等，还要灵活运用运算律，以提高运算速度及准确性