3.1.2.2 分段函数 随堂跟踪练习(含答案)
文档属性
| 名称 | 3.1.2.2 分段函数 随堂跟踪练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 11:30:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.1.2.2 分段函数跟踪练习
(15分钟 30分)
1.已知函数f(x)=若f(x)=5,则x的值是 ( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
2.函数f(x)=x2-2|x|的图象是 ( )
3.已知f(x)=则不等式xf(x)+x≤2的解集是 ( )
A.{x|x≤1} B.{x|x≤2}
C.{x|0≤x≤1} D.{x|x<0}
4.(2020·西城高一检测)因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况的是_______(写出所有正确的图标序号).?
5.已知函数f(x)=求:(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
(20分钟 40分)
一、单选题(每小题5分,共15分)
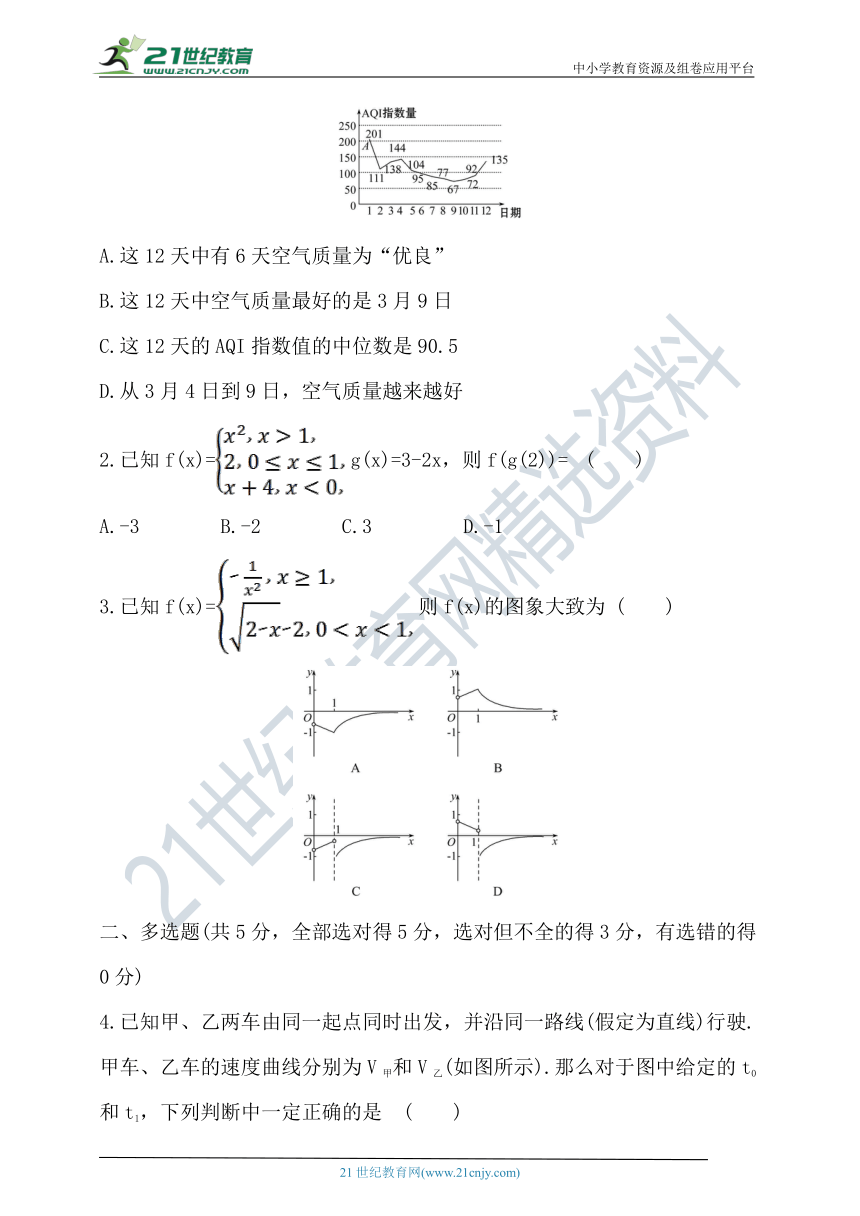
1.(2020·武汉高一检测)AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日AQI指数值的统计数据,图中点A表示3月1日的AQI指数值为201.则下列叙述不正确的是 ( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是3月9日
C.这12天的AQI指数值的中位数是90.5
D.从3月4日到9日,空气质量越来越好
2.已知f(x)=g(x)=3-2x,则f(g(2))= ( )
A.-3 B.-2 C.3 D.-1
3.已知f(x)=则f(x)的图象大致为 ( )
二、多选题(共5分,全部选对得5分,选对但不全的得3分,有选错的得0分)
4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是 ( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
三、填空题(每小题5分,共10分)
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月交水费16m元,则该职工这个月实际用水量为_______立方米.?
【补偿训练】
若函数f(x)=则f(-3)=______________ .?
6.已知函数f(x)=则f(1)=_______,若f(f(0))=a,则实数a=_______.?
四、解答题
7.(10分)已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
解析版
(15分钟 30分)
1.已知函数f(x)=若f(x)=5,则x的值是 ( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
【解析】选A.由题意知,当x≤0时,f(x)=x2+1=5,得x=-2(x=2舍去);
当x>0时,f(x)=-2x=5,得x=-,舍去.
【误区警示】本题容易出现忽视各段自变量的取值对x值的限制,出现错解.
2.函数f(x)=x2-2|x|的图象是 ( )
【解析】选C.f(x)=分段画出.
3.已知f(x)=则不等式xf(x)+x≤2的解集是 ( )
A.{x|x≤1} B.{x|x≤2}
C.{x|0≤x≤1} D.{x|x<0}
【解析】选A.当x≥0时,f(x)=1,xf(x)+x≤2?x≤1,所以0≤x≤1;
当x<0时,f(x)=0,xf(x)+x≤2?x≤2,所以x<0.
综上,x≤1.
4.(2020·西城高一检测)因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况的是_______(写出所有正确的图标序号).?
【解析】图①③所反映的是公司会挣钱,而图②公司会亏本;
所以反映了这种物资每份价格(单位:万元)的可能变化情况的是①③.
答案:①③
5.已知函数f(x)=求:(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【解析】(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f(f(3))=f(-5)=1-2×(-5)=1+10=11.
(3)当-4≤x<0时,1当x=0时,f(0)=2;当0综上f(x)取值的集合为(-5,9].
(20分钟 40分)
一、单选题(每小题5分,共15分)
1.(2020·武汉高一检测)AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日AQI指数值的统计数据,图中点A表示3月1日的AQI指数值为201.则下列叙述不正确的是 ( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是3月9日
C.这12天的AQI指数值的中位数是90.5
D.从3月4日到9日,空气质量越来越好
【解析】选C.根据图象:有6天AQI指数小于100,
所以这12天中有6天空气质量为“优良”,所以A叙述正确;这12天中,AQI指数的最小值是3月9日的67,
所以12天中空气质量最好的是3月9日,所以B叙述正确;由图象知,AQI指数值的中位数是=99.5,所以C叙述错误;通过图象可以看出,从3月4日到9日,AQI的值逐渐减小,即空气质量越来越好,所以D叙述正确.
2.已知f(x)=g(x)=3-2x,则f(g(2))= ( )
A.-3 B.-2 C.3 D.-1
【解析】选C.因为g(x)=3-2x,所以g(2)=3-2×2=-1<0,所以f(g(2))=f(-1)=-1+4=3.
3.已知f(x)=则f(x)的图象大致为 ( )
【解析】选A.由f(2)=-<0,排除选项B;
f=-2+<0,排除选项D;
函数在x=1处是连续的,排除C.
二、多选题(共5分,全部选对得5分,选对但不全的得3分,有选错的得0分)
4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是 ( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
【解析】BD.由图可知,当时间为t1时,甲车的速度小于乙车的速度;t0时刻之前,甲车的速度一直大于乙车,时间相同的情况下,甲车行驶路程大于乙车行驶路程,故t0时刻甲车在乙车前面;t0时刻后,甲车的速度小于乙车的速度.
三、填空题(每小题5分,共10分)
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月交水费16m元,则该职工这个月实际用水量为_______立方米.?
【解析】设该单位职工每月应交水费为y元,实际用水量为x立方米,
则y=
由y=16m,可知x>10.
令2mx-10m=16m,
解得x=13.
答案:13
【补偿训练】
若函数f(x)=则f(-3)=______________ .?
【解析】f(-3)=f(-3+2)=f(-1)
=f(-1+2)=f(1)=f(1+2)=f(3)=2×3=6.
答案:6
6.已知函数f(x)=则f(1)=_______,若f(f(0))=a,则实数a=_______.?
【解析】依题意知f(1)=3+2=5;f(0)=3×0+2=2,则f(f(0))=f(2)=22-2a=a,求得a=.
答案:5
四、解答题
7.(10分)已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【解析】(1)f(x)=g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,
即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
_21?????????è?????(www.21cnjy.com)_
3.1.2.2 分段函数跟踪练习
(15分钟 30分)
1.已知函数f(x)=若f(x)=5,则x的值是 ( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
2.函数f(x)=x2-2|x|的图象是 ( )
3.已知f(x)=则不等式xf(x)+x≤2的解集是 ( )
A.{x|x≤1} B.{x|x≤2}
C.{x|0≤x≤1} D.{x|x<0}
4.(2020·西城高一检测)因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况的是_______(写出所有正确的图标序号).?
5.已知函数f(x)=求:(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
(20分钟 40分)
一、单选题(每小题5分,共15分)
1.(2020·武汉高一检测)AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日AQI指数值的统计数据,图中点A表示3月1日的AQI指数值为201.则下列叙述不正确的是 ( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是3月9日
C.这12天的AQI指数值的中位数是90.5
D.从3月4日到9日,空气质量越来越好
2.已知f(x)=g(x)=3-2x,则f(g(2))= ( )
A.-3 B.-2 C.3 D.-1
3.已知f(x)=则f(x)的图象大致为 ( )
二、多选题(共5分,全部选对得5分,选对但不全的得3分,有选错的得0分)
4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是 ( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
三、填空题(每小题5分,共10分)
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月交水费16m元,则该职工这个月实际用水量为_______立方米.?
【补偿训练】
若函数f(x)=则f(-3)=______________ .?
6.已知函数f(x)=则f(1)=_______,若f(f(0))=a,则实数a=_______.?
四、解答题
7.(10分)已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
解析版
(15分钟 30分)
1.已知函数f(x)=若f(x)=5,则x的值是 ( )
A.-2 B.2或-
C.2或-2 D.2或-2或-
【解析】选A.由题意知,当x≤0时,f(x)=x2+1=5,得x=-2(x=2舍去);
当x>0时,f(x)=-2x=5,得x=-,舍去.
【误区警示】本题容易出现忽视各段自变量的取值对x值的限制,出现错解.
2.函数f(x)=x2-2|x|的图象是 ( )
【解析】选C.f(x)=分段画出.
3.已知f(x)=则不等式xf(x)+x≤2的解集是 ( )
A.{x|x≤1} B.{x|x≤2}
C.{x|0≤x≤1} D.{x|x<0}
【解析】选A.当x≥0时,f(x)=1,xf(x)+x≤2?x≤1,所以0≤x≤1;
当x<0时,f(x)=0,xf(x)+x≤2?x≤2,所以x<0.
综上,x≤1.
4.(2020·西城高一检测)因市场战略储备的需要,某公司1月1日起,每月1日购买了相同金额的某种物资,连续购买了4次.由于市场变化,5月1日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中没有亏本,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况的是_______(写出所有正确的图标序号).?
【解析】图①③所反映的是公司会挣钱,而图②公司会亏本;
所以反映了这种物资每份价格(单位:万元)的可能变化情况的是①③.
答案:①③
5.已知函数f(x)=求:(1)画出函数f(x)的简图(不必列表).
(2)求f(f(3))的值.
(3)当-4≤x<3时,求f(x)取值的集合.
【解析】(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f(f(3))=f(-5)=1-2×(-5)=1+10=11.
(3)当-4≤x<0时,1
(20分钟 40分)
一、单选题(每小题5分,共15分)
1.(2020·武汉高一检测)AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地3月1日到12日AQI指数值的统计数据,图中点A表示3月1日的AQI指数值为201.则下列叙述不正确的是 ( )
A.这12天中有6天空气质量为“优良”
B.这12天中空气质量最好的是3月9日
C.这12天的AQI指数值的中位数是90.5
D.从3月4日到9日,空气质量越来越好
【解析】选C.根据图象:有6天AQI指数小于100,
所以这12天中有6天空气质量为“优良”,所以A叙述正确;这12天中,AQI指数的最小值是3月9日的67,
所以12天中空气质量最好的是3月9日,所以B叙述正确;由图象知,AQI指数值的中位数是=99.5,所以C叙述错误;通过图象可以看出,从3月4日到9日,AQI的值逐渐减小,即空气质量越来越好,所以D叙述正确.
2.已知f(x)=g(x)=3-2x,则f(g(2))= ( )
A.-3 B.-2 C.3 D.-1
【解析】选C.因为g(x)=3-2x,所以g(2)=3-2×2=-1<0,所以f(g(2))=f(-1)=-1+4=3.
3.已知f(x)=则f(x)的图象大致为 ( )
【解析】选A.由f(2)=-<0,排除选项B;
f=-2+<0,排除选项D;
函数在x=1处是连续的,排除C.
二、多选题(共5分,全部选对得5分,选对但不全的得3分,有选错的得0分)
4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图所示).那么对于图中给定的t0和t1,下列判断中一定正确的是 ( )
A.在t1时刻,甲车的速度大于乙车的速度
B.t0时刻后,甲车的速度小于乙车的速度
C.在t0时刻,两车的位置相同
D.在t0时刻,甲车在乙车前面
【解析】BD.由图可知,当时间为t1时,甲车的速度小于乙车的速度;t0时刻之前,甲车的速度一直大于乙车,时间相同的情况下,甲车行驶路程大于乙车行驶路程,故t0时刻甲车在乙车前面;t0时刻后,甲车的速度小于乙车的速度.
三、填空题(每小题5分,共10分)
5.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10立方米的,按每立方米m元收费;用水量超过10立方米的,超过部分按每立方米2m元收费.某职工某月交水费16m元,则该职工这个月实际用水量为_______立方米.?
【解析】设该单位职工每月应交水费为y元,实际用水量为x立方米,
则y=
由y=16m,可知x>10.
令2mx-10m=16m,
解得x=13.
答案:13
【补偿训练】
若函数f(x)=则f(-3)=______________ .?
【解析】f(-3)=f(-3+2)=f(-1)
=f(-1+2)=f(1)=f(1+2)=f(3)=2×3=6.
答案:6
6.已知函数f(x)=则f(1)=_______,若f(f(0))=a,则实数a=_______.?
【解析】依题意知f(1)=3+2=5;f(0)=3×0+2=2,则f(f(0))=f(2)=22-2a=a,求得a=.
答案:5
四、解答题
7.(10分)已知函数f(x)=|x+1|+|x-2|,g(x)=|x-3|.
(1)在平面直角坐标系里作出f(x),g(x)的图象.
(2)?x∈R,用min(x)表示f(x),g(x)中的较小者,记作min(x)={f(x),g(x)},请用图象法和解析法表示min(x).
(3)求满足f(x)>g(x)的x的取值范围.
【解析】(1)f(x)=g(x)=
则对应的图象如图:
(2)min(x)图象如图:
解析式为min(x)=
(3)若f(x)>g(x),
则由图象知在A点左侧,B点右侧满足条件.
此时对应的x满足x>0或x<-2,
即不等式f(x)>g(x)的解集为(-∞,-2)∪(0,+∞).
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
