沪教版(上海)八下数学22.8(2)平面向量加法课件(共13张ppt)
文档属性
| 名称 | 沪教版(上海)八下数学22.8(2)平面向量加法课件(共13张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
22.8平面向量的加法(2)
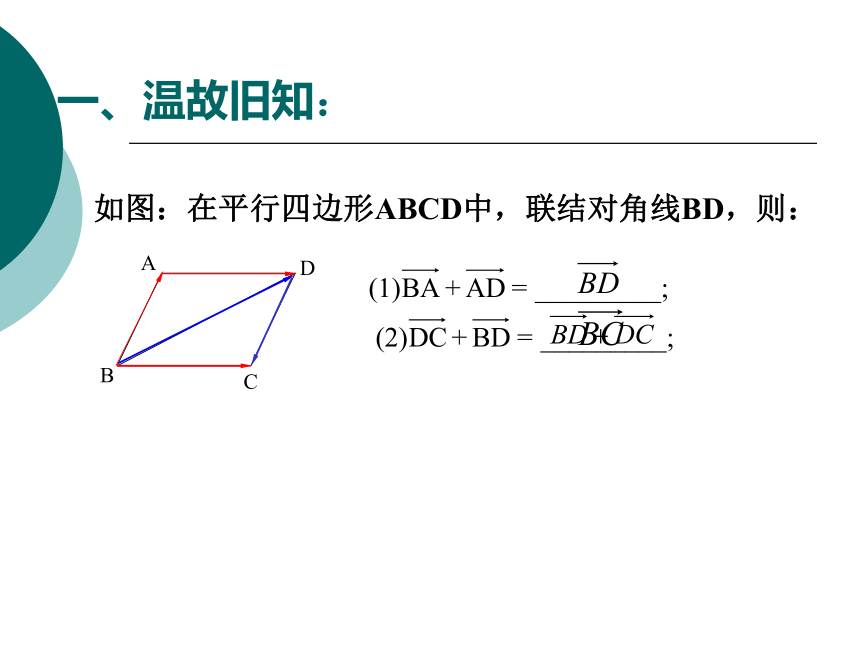
一、温故旧知:
A
B
C
D
如图:在平行四边形ABCD中,联结对角线BD,则:
A
B
C
D
你能得到什么结论?
当三个向量顺次首尾相接时,这三个向量相加所得的和向量是以
_____________为起点,________________为终点的向量.
第一个向量的起点
第三个向量的终点
所以,
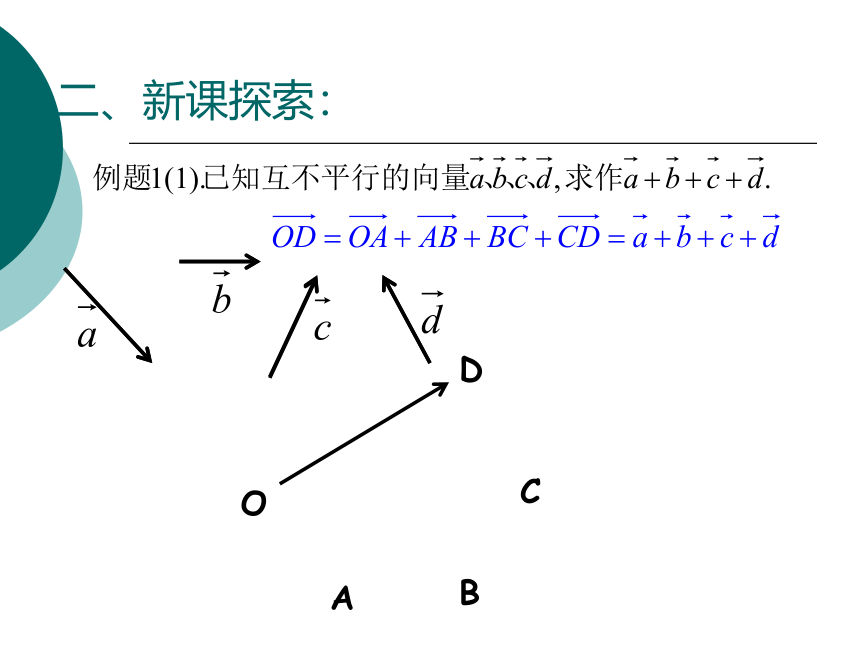
二、新课探索:
O
A
B
C
D
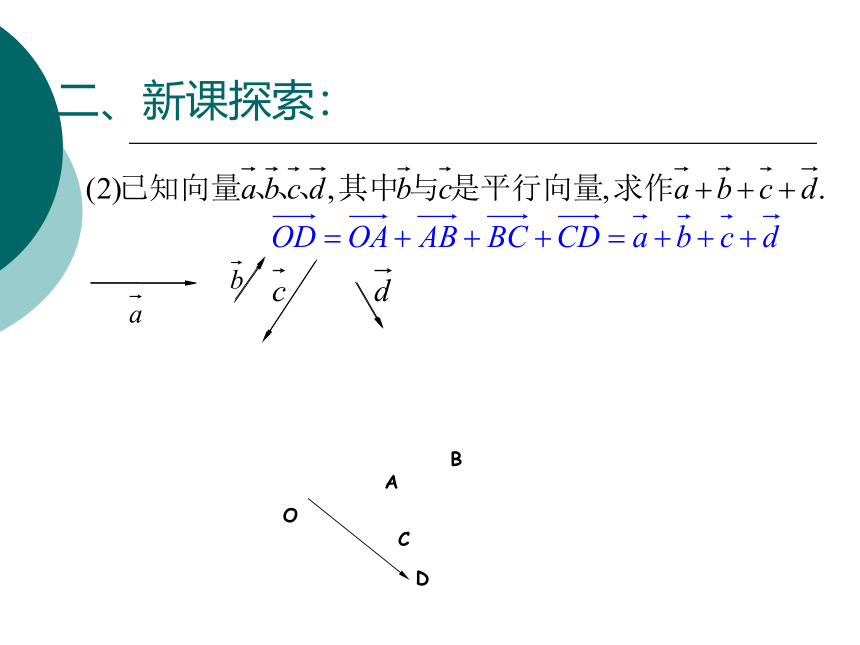
二、新课探索:
O
A
B
C
D
二、新课探索:
二、新课探索:
你能归纳出几个向量相加的法则吗?
一般地,几个向量相加,可把这几个向量_______________,
那么它们的和向量是以_____________________为起点,
_________________为终点的向量.
这样的规定叫做几个向量相加的多边形法则.
顺次首尾相接
第一个向量的起点
最后一个向量的终点
二、新课探索:
二、新课探索:
例题2
如图,已知梯形ABCD中,AB∥DC,点E在AB上,EC∥AD.在图中指出下列几个向量的和向量:
三、课内训练:
三、课内训练:
3.如图,已知五边形ABCDE,适当选用它的几条边作向量,把下列向量分别用所选定的向量的关系式表示出来:
三、课内训练:
教材P112
(第2题).如图,已知五边形ABCDE,适当选用它的几条边(除DC外)作向量,把下列向量分别用所选定的向量的关系式表示出来:
四、本课小结:
本节课我们学习了…
你有哪些收获?
1.几个向量相加的多边形法则:
一般地,几个向量相加,可把这几个向量顺次首尾相接,
那么它们的和向量是以第一个向量的起点为起点,
最后一个向量的终点为终点的向量.
2.在化简几个向量的加法算式时(如例2),可以先找出几个
已经首尾相连的向量,利用多边形法则或三角形法则得到
这几个向量的和向量,再利用数形结合等方法将算式化简.
总之,学习向量的加减法,数形结合是非常有用的方法.
练习册22.8(2)
五、作业布置:
22.8平面向量的加法(2)
一、温故旧知:
A
B
C
D
如图:在平行四边形ABCD中,联结对角线BD,则:
A
B
C
D
你能得到什么结论?
当三个向量顺次首尾相接时,这三个向量相加所得的和向量是以
_____________为起点,________________为终点的向量.
第一个向量的起点
第三个向量的终点
所以,
二、新课探索:
O
A
B
C
D
二、新课探索:
O
A
B
C
D
二、新课探索:
二、新课探索:
你能归纳出几个向量相加的法则吗?
一般地,几个向量相加,可把这几个向量_______________,
那么它们的和向量是以_____________________为起点,
_________________为终点的向量.
这样的规定叫做几个向量相加的多边形法则.
顺次首尾相接
第一个向量的起点
最后一个向量的终点
二、新课探索:
二、新课探索:
例题2
如图,已知梯形ABCD中,AB∥DC,点E在AB上,EC∥AD.在图中指出下列几个向量的和向量:
三、课内训练:
三、课内训练:
3.如图,已知五边形ABCDE,适当选用它的几条边作向量,把下列向量分别用所选定的向量的关系式表示出来:
三、课内训练:
教材P112
(第2题).如图,已知五边形ABCDE,适当选用它的几条边(除DC外)作向量,把下列向量分别用所选定的向量的关系式表示出来:
四、本课小结:
本节课我们学习了…
你有哪些收获?
1.几个向量相加的多边形法则:
一般地,几个向量相加,可把这几个向量顺次首尾相接,
那么它们的和向量是以第一个向量的起点为起点,
最后一个向量的终点为终点的向量.
2.在化简几个向量的加法算式时(如例2),可以先找出几个
已经首尾相连的向量,利用多边形法则或三角形法则得到
这几个向量的和向量,再利用数形结合等方法将算式化简.
总之,学习向量的加减法,数形结合是非常有用的方法.
练习册22.8(2)
五、作业布置:
