2020-2021学年人教版五年级数学下册《第7章 折线统计图》单元测试题(含解析)
文档属性
| 名称 | 2020-2021学年人教版五年级数学下册《第7章 折线统计图》单元测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-22 22:36:40 | ||
图片预览



文档简介
2020-2021学年人教版五年级数学下册《第7章
折线统计图》单元测试题
一.选择题(共8小题)
1.某市规定每户用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨水价为3元.下图能表示每月水费与用水量关系的示意图是( )
A.
B.
C.
D.
2.星期天,林林从家出发到书店买故事书,然后回到家里,下面第( )幅图描述的是林林的行为.
A.
B.
C.
3.如图是甜甜从家出发到莲花山公园去玩再返回的图,根据图中的信息,下面说法错误的是( )
A.甜甜家距莲花山公园6千米
B.甜甜在去的路上休息了20分钟
C.甜甜在莲花山公园玩了1小时
D.甜甜返回时的速度是18千米/小时
4.下面事件中,( )最适合用如图来表示.
A.某校六个班的人数
B.某个月中6天的天气情况
C.六个好朋友每天看书时间统计
D.张明近几年的身高情况.
5.妈妈带小华去公园玩.她们从家出发,直接到了公园,然后她们在公园里玩了几小时,在返回的路上买了瓶水后就径直回家了.下面
( )幅图描述的是上面的情景.
A.
B.
C.
6.如图是甲、乙两个城市今年上半年月平均气温统计图,从图中可以看出,乙城市月平均气温高于甲城市的有( )个月.
A.2
B.3
C.4
D.5
7.如图所示的图象表示斑马和长颈鹿的奔跑情况,下面的说法不符合这个图象的是( )
A.斑马奔跑的路程与奔跑的时间成比例
B.长颈鹿25分钟跑了20千米
C.长颈鹿比斑马跑得快
D.斑马跑12千米用了10分钟
8.星期天王叔叔和李叔叔两家自驾车去游玩.两辆车从同一地点同时出发,行至十字路口时,王叔叔的车刚刚驶过,红灯亮起,李叔叔只能停下.绿灯亮起时,李叔叔继续前行追赶王叔叔,结果李叔叔比王叔叔提前到达目的地与上述文字描述相吻合的图是( )
A.
B.
C.
二.填空题(共8小题)
9.根据甲、乙两车的行程图填空.
(1)甲车时速是
千米/时.
(2)甲乙两车时速的差是
千米/时.
(3)甲乙两车速度的比是
.
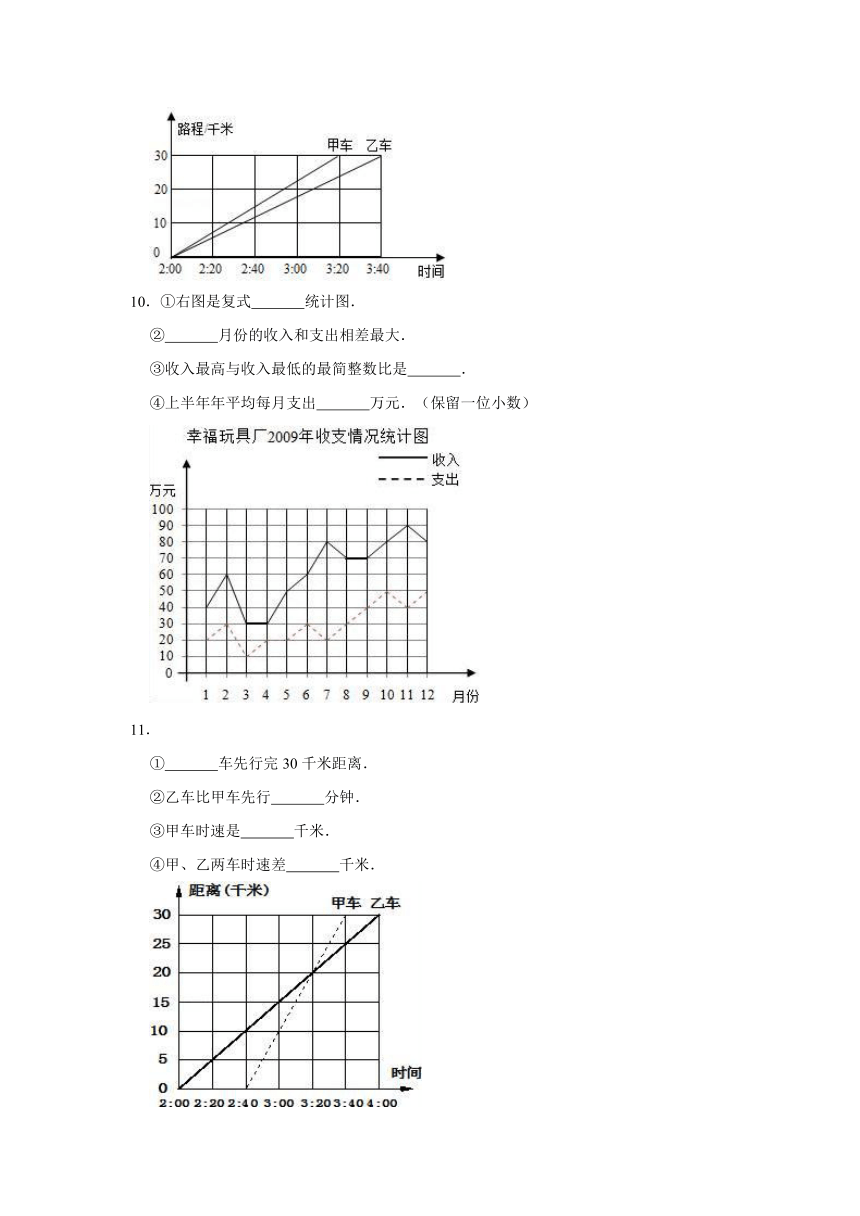
10.①右图是复式
统计图.
②
月份的收入和支出相差最大.
③收入最高与收入最低的最简整数比是
.
④上半年年平均每月支出
万元.(保留一位小数)
11.
①
车先行完30千米距离.
②乙车比甲车先行
分钟.
③甲车时速是
千米.
④甲、乙两车时速差
千米.
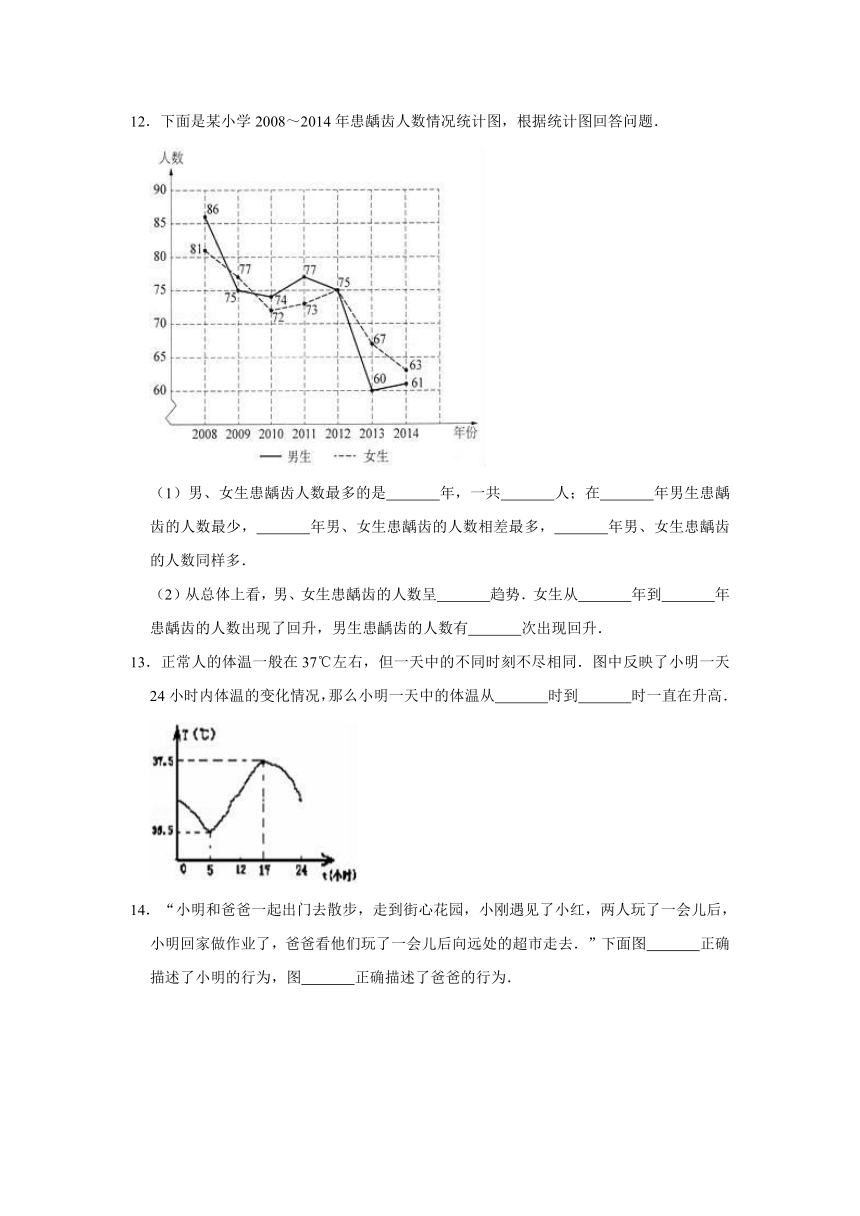
12.下面是某小学2008~2014年患龋齿人数情况统计图,根据统计图回答问题.
(1)男、女生患龋齿人数最多的是
年,一共
人;在
年男生患龋齿的人数最少,
年男、女生患龋齿的人数相差最多,
年男、女生患龋齿的人数同样多.
(2)从总体上看,男、女生患龋齿的人数呈
趋势.女生从
年到
年患龋齿的人数出现了回升,男生患齲齿的人数有
次出现回升.
13.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同.图中反映了小明一天24小时内体温的变化情况,那么小明一天中的体温从
时到
时一直在升高.
14.“小明和爸爸一起出门去散步,走到街心花园,小刚遇见了小红,两人玩了一会儿后,小明回家做作业了,爸爸看他们玩了一会儿后向远处的超市走去.”下面图
正确描述了小明的行为,图
正确描述了爸爸的行为.
15.某服装厂一、二车间产值情况统计如图.
(1)纵轴上每个单位长度表示
万元.
(2)一车间平均每季度产值
万元,二车间平均每季度产值
万元.
(3)第二季度一车间产值比二车间多
万元,二车间第三季度产值比第二季度多
万元.
16.下面的图象表示甲乙两辆汽车行驶的时间和路程.
(1)行驶12千米甲汽车比乙汽车大约少用
分.
(2)按这样的速度,行驶500千米,甲汽车要行驶
小时,乙汽车要行驶
小时.
三.操作题(共2小题)
17.如图是某便利店两种品牌的纯牛奶1﹣6月销售情况统计表.
月份
1
2
3
4
5
6
销量
甲
20
25
35
40
50
55
乙
15
18
20
16
12
10
请制成复式折线统计图,并回答问题:
(1)你了解到哪些信息?
(2)如果你是便利店经理,下月你准备怎样进货?为什么?
18.下面是明德小学2014年一~六年级植树情况统计图.
①二年级植树的棵数是
棵,六年级植树的棵数是
棵.
②植树最多的年级是
年级,植树最少的年级是
,它们相差
棵.
四.应用题(共10小题)
19.王林和马军参加1000米的长跑比赛,下图中的两条折线分别表示两人在途中的情况,看图回答问题.
(1)跑完1000米,马军用了
分钟,
(填姓名)比赛赢了.
(2)起跑后的第1分钟,
速度快一些.第
分钟,两人跑的路程相同,是
米.
(3)王林的平均速度是
米/分.
20.客车从A地开往B地,货车从B地开往A地,它们行驶的情况如图.
(1)观察如图,两车开出多少小时后相遇?
(2)货车每小时约行多少千米?
(3)客车在距B地多少千米的地方停留了多长时间?停留前后的速度相同吗?
(4)估一估:当货车到达A地时,客车距B地还有多少千米?按照它的行驶速度,到B地还需多少小时?
(5)假若客车不在途中停留,请你用你喜欢的方法求出两车开出多少小时后就能相遇.
21.小刚骑车到离家6千米的一个公园游玩.根据折线图解答下列问题.
(1)小刚在公园玩了多长时间?
(2)如果一直骑车,不休息,他什么时候可以到达公园?
22.振兴玩具厂1~5月的产值如图所示.
(1)这是一幅
统计图,横轴表示
,纵轴表示
,每格代表
.
(2)产值最高的是
月,5月的产值比4月的产值增加了
万元.
(3)该厂第一季度平均每月的产值是
.该厂的每月产值是呈
趋势.(填“上升”或“下降”)
(4)这种统计图的优点是
.
23.下面是某市一中和二中篮球队的五场比赛得分情况统计图.
(1)两个学校的篮球队第二场比赛时成绩相差多少分?
(2)哪场比赛两个学校的篮球队成绩相差最大?
24.如图的折线图表示的是乌龟和兔子赛跑时路程和时间的关系.
(1)前5分乌龟和兔子的速度各是多少?按这样的速度,兔子应比乌龟早到几分?
(2)实际上兔子中途睡了几分?乌龟比兔子早到几分?
25.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
26.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
27.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
28.某市甲,乙两所学校学生参加课外活动情况统计图如下.
(1)哪﹣年两校参加课外活动的人数相差最多?相差多少人?
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有多少人,乙校参加课外活动的有多少人?
(3)甲校参加课外活动的人数在哪个时间段上升最多?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】由题意可知:每户每月用水量不超过10吨,每吨价格为2.5元;即10吨以内,每吨水的单价变化不大,然后水量超过10吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即可
【解答】解:由分析知:每户每月用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨价格为3元.下面4幅图中能表示每月水费与用水量关系的是C;
故选:C.
【点评】此题应根据单价和用水吨数之间的关系进行判断.
2.【分析】根据题意,结合图示,图A表明小明从家出发后有折回家中,然后再从家出发到达书店停留了一会就再次返回家中,符合题意;图B显然不正确,没有在书店停留的时间;图C显示不正确,出发地点不是从家出发;据此解答.
【解答】解:A:表明小明从家出发后有折回家中,然后再从家出发到达书店停留了一会就再次返回家中,符合题意;
B:没有在书店停留的时间,所以此描述错误;
C:出发地点不是从家出发;所以不正确.
所以,图A比较准确地描述了上面的情景.
故选:A.
【点评】此题为一次折线图象与实际结合的题型,同学们要培养从图形中找信息的能力.
3.【分析】根据图象分析出甜甜从家出发到莲花山公园去玩再返回的家的过程,进而判断即可.
【解答】解:由折线统计图可以看出,纵轴上数据表示路程,单位是千米,每格代表1千米,甜甜家到莲花山公园相距6格,即6千米,所以A说法正确;
根据图示可以看出甜甜从家出发到莲花山公园的路上休息了20分钟,所以B说法正确;
10时到达莲花山公园,10时40分开始回家,所以在莲花山公园玩了40分钟,不是玩了1小时,所以C说法错误;
用路程除以甜甜返回用的时间就是甜甜返回时速度,6÷=18(千米),所以D计算正确;
故选:C.
【点评】本题主要考查了学生能正确根据折线统计图发现问题并解决问题的能力.
4.【分析】根据折线统计图的特点及作用,折线统计图不仅能表示数量的多少,而且能反映出数量之间的增减变化的趋势.
【解答】解:A,表示某校六个班的人数,选用条形统计图;
B,表示某个月中6天的天气情况,选用条形统计图;
C,表示六个好朋友每天看书的时间统计,选用折线统计图;
D,表示张明近几年的身高情况,选用折线统计图;但是它的身高是逐渐增高,而不是下降.所以此图不符合张明近几年的身高情况.
因此,以上事件能用此图表示的是六个好朋友每天看书的时间统计.
故选:C.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用.
5.【分析】根据运动的路程与时间判断折线图象.注意几个行走段:“她们从家出发,直接到了公园”此时的折线应呈上升趋势,“她们在公园里玩了几小时”此时的折线应处于持平,“在返回的路上买了瓶水后就径直回家了”此时的折线应处于小幅度的持平然后再下降.
【解答】解:A:表示小华和妈妈从家出发直接到公园后没有停留,而在返回途中停留的时间较长(买水),最后买完水后直接回家,因为没有表示出在公园的停留时间,所以错误;
B:根据图示,第一处停留表示在公园里玩耍,第二处停留表示买水,图B表示玩耍的时间小于买水的时间,所以此描述错误;
C:根据图示,第一处停留表示在公园里玩耍,第二处停留表示买水,图C表示玩耍的时间大于买水的时间,所以图C描述正确;
故选:C.
【点评】此题为一次折线图象与实际结合的题型,同学们要培养从图形中找信息的能力.
6.【分析】通过观察折线统计图可知,乙城市的月平均气温高于甲城市的月平均气温有3月和4月。据此解答。
【解答】解:乙城市的月平均气温高于甲城市的月平均气温有3月和4月。
答:乙城市月平均气温高于甲城市的有2个月。
故选:A。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
7.【分析】根据图象对各选项进行依次分析、进而得出结论.
【解答】解:A、因为12÷10=1.2千米,24÷20=1.2千米,…,即斑马奔跑的路程÷奔跑的时间=斑马速度(一定),所以奔跑的路程与奔跑的时间成正比例;
B、由图象可知:长颈鹿25分钟跑了20千米;
C、由图象可知:斑马比长颈鹿跑的快,所以C选项长颈鹿比斑马跑得快,说法错误;
D、由图象可知:斑马跑12千米用了10分钟;
故选:C.
【点评】此题考查了学生根据统计图获取信息的能力,能够根据图象提出问题并能解决问题的能力.
8.【分析】根据题意和各个统计图中的图象,可以判断出哪个统计图中的图象与题目中的文字描述相吻合.
【解答】解:A统计图符合题意;
B统计图中李叔叔到达终点晚于王叔叔,与题目中果李叔叔比王叔叔提前到达目的地矛盾,故选项B不符合题意;
C统计图中刚开始李叔叔比王叔叔行驶的快,与题干中两辆车从同一地点同时出发,行至十字路口时,王叔叔的车刚刚驶过,红灯亮起,李叔叔只能停下矛盾,故选项C不符合题意;
故选:A.
【点评】此题主要考查复式折线统计图,明确题意,可以判断出哪个选项中的图象与题目中的文字吻合是解答本题的关键.
二.填空题(共8小题)
9.【分析】(1)甲车在1小时20分钟内行驶了30千米,可根据公式:路程÷时间=速度进行计算即可得到答案;
(2)乙车在1小时40分钟的时间内行驶了30千米,根据公式计算出乙车行驶的速度,然后再用甲车的速度减去乙车的速度即可得到答案;
(3)可用路程÷时间=速度分别计算出甲乙的速度,然后再比用甲、乙两车的速度相比即可.
【解答】解:(1)1时20分钟=1小时
30÷1=22.5(千米)
答:甲车时速22.5千米.
(2)1时40分钟=1小时,
乙车的速度为:30÷1=18(千米),
甲乙两车时速之差是:22.5﹣18=4.5(千米),
答:甲乙两车时速之差是4.5千米;
(3)22.5:4.5=(22.5÷4.5):(4.5÷4.5)=5:1
答:甲乙两车速度的比是
5:1.
故答案为:(1)22.5,(2)4.5,(3)5:1
【点评】此题主要考查的是如何从统计图中获取信息,然后再根据所得到的信息进行计算即可,此题主要用到的公式是速度=路程÷时间.
10.【分析】①观察可知,此图为复式折线统计图;
②通过观察统计图,可知7月份的收入和支出相差最大;
③收入最高的是11月份,是90万元;收入最低的是3和4月份,都是30万元,进而写出收入最高与收入最低的整数比,再根据比的性质化成最简比;
④用上半年,即1﹣6月份的总支出除以月份数6即可.
【解答】解:①右图是复式
折线统计图;
②7月份的收入和支出相差最大;
③收入最高与收入最低的比是:90:30=3:1;
④(20+30+10+20+20+30)÷6,
=130÷6,
≈21.7(万元);
答:上半年年平均每月支出
21.7万元.
故答案为:折线,7,3:1,21.7.
【点评】此题主要考查的是如何观察复式折线统计图,并从统计图中获取有用的信息,进行分析、解决问题.
11.【分析】①观察统计图,可知甲车行完30千米距离时的时刻是3:40,而乙车行完30千米距离时的时刻是4:00,所以甲车先行完的30千米距离;
②甲车开始行驶的时刻是2:40,乙车开始行驶的时刻是2:00,用2:40减去2:00,就是乙车比甲车先行的时间;
③甲车开始行驶的时刻是2:40,行完30千米的时刻是3:40,先求出甲车行驶的时间,进而根据路程÷时间=速度求出甲车的时速;
④乙车开始行驶的时刻是2:00,行完30千米的时刻是4:00,先求出乙车行驶的时间,进而根据路程÷时间=速度求出甲车的时速,再求得甲、乙两车时速差.
【解答】解:①根据分析,可知甲车先行完的30千米距离;
②2时40分﹣2时=40分.
答:乙车比甲车先行40分钟.
③3时40分﹣2时40分=1小时
30÷1=30(千米).
答:甲车时速是309千米.
④4时﹣2时=2小时
30÷2=15(千米)
30﹣15=15(千米).
答:甲、乙两车时速差15千米.
故答案为:甲,40,30,15.
【点评】此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法.
12.【分析】(1)找出这两条线的最高点,就是这一年男生、女生患龋齿的人数最多的年份,即2008年,然后再把人数相加,即86+81=167人;
找出这实线的最低点,就是男生患龋齿的人数最少的年份,即2013年;
找出这两条线的差距最大的点,就是男、女生患龋齿的人数相差最多的年份,即2013年;
找出这两条线的差距相交的点,就是男、女生患龋齿的人数同样多的年份,即2012年;
(2)根据折线的总体变化趋势,从总体上看,男、女生患龋齿的人数呈下降趋势.女生从2011年到2012年患龋齿的人数出现了回升,男生患齲齿的人数有2次出现回升.据此解答.
【解答】解:(1)男、女生患龋齿人数最多的是2008年,一共167人;在2013年男生患龋齿的人数最少,2013年男、女生患龋齿的人数相差最多,2012年男、女生患龋齿的人数同样多.
(2)从总体上看,男、女生患龋齿的人数呈下降趋势.女生从2011年到2012年患龋齿的人数出现了回升,男生患齲齿的人数有2次出现回升.
故答案为:2008,167,2013,2013,2012;下降,2011,2012,2.
【点评】本题主要考查了如何从折线统计图读出数据,以及判断变化趋势,根据问题选择合适的数据进行解答.
13.【分析】分析折线统计图,折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,从5时到17时,小明的体温一直是升高的趋势,从而可求出答案.
【解答】解:由折线统计图可知:折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,则小明这一天的体温范围是36.5≤T≤37.5;从5时到17时,小明的体温一直是升高的趋势,而17﹣24时的体温是下降的趋势.
所以那么小明一天中的体温从
5时到
17时一直在升高.
故答案为:5,17.
【点评】读懂统计图,从图中得到必要的信息是解决本题的关键.
14.【分析】由于小明和爸爸一起去散步,从家到街心花园,小明遇见了小红,两人玩了一会儿后,小明回家做作业了,用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;爸爸看他们玩了一会儿后向远处的超市走去,用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远,据此解答.
【解答】解:小明用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;
爸爸用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远.
故选:C,B.
【点评】本题是一个信息题目,主要利用图象信息找到所需要的数量关系,然后利用这些关系即可确定图象.
15.【分析】(1)通过观察统计图可知,纵轴上每个单位长度表示100万元.
(2)根据求平均数的方法,先分别求出一车间、二车间全年的总产值,然后分别除以4即可.
(3)根据求一个数比另一个数多几,用减法解答.
【解答】解:(1)纵轴上每个单位长度表示100万元.
(2)(250+360+510+340)÷4
=1460÷4
=365(万元)
(200+250+300+230)÷4
=980÷4
=245(万元)
答:一车间平均每季度产值是365万元,二车间平均每季度产值是245万元.
(3)360﹣250=110(万元)
300﹣250=50(万元)
答:第二季度一车间产值比二车间多110万元,二车间第三季度产值比第二季度多50万元.
故答案为:100;365、245;110、50,.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
16.【分析】(1)找出路程是12千米时,甲、乙两汽车的直线图上对应的时间,两时间的差就是答案;
(2)利用路程÷时间=速度分别计算出甲乙两车的行驶速度,然后再用500千米分别除以甲乙两车的速度即可得到需要行驶的时间.
【解答】解:(1)12﹣6=6(分)
答:行驶12千米甲汽车比乙汽车大约少用
6分;
(2)甲车:500÷(16÷8)
=500÷2
=250(分钟)
≈4.17(小时)
乙车:500÷(12÷12)
=500÷1
=500(分钟)
≈8.33(小时)
答:甲汽车要行驶
4.17小时,乙汽车要行驶
8.33小时.
故答案为:6,4.17、8.33.
【点评】解答此图的关键是,会看懂此表,根据速度,路程,时间的关系,找出数量关系,找准对应量,列式解答即可.
三.操作题(共2小题)
17.【分析】首先根据数据描出各点,再顺次连接即可.
(1)了解到甲品牌的销售量越来越多,乙品牌的销售量越来越少.
(2)如果是便利店经理,下月准备多进一些甲品牌的纯牛奶,因为甲品牌的销售量越来越多.
【解答】解:画图如下,
(1)了解到甲品牌的销售量越来越多,乙品牌的销售量越来越少.
(2)如果是便利店经理,下月准备多进一些甲品牌的纯牛奶,因为甲品牌的销售量越来越多.
【点评】此题主要考查了统计图表的填补,以及从统计图表中获取信息的能力,要熟练掌握.
18.【分析】①根据统计图中的数据判断解答.
②植树最多的是五年级,植树最少的是一年级,用五年级植树的棵数减去一年级植树的棵数就是相差的棵数.
【解答】解:①二年级植树的棵数是305棵,六年级植树的棵数是500棵.
②645﹣200=445(棵)
答:植树最多的年级是五年级,植树最少的年级是一年级,它们相差445棵.
故答案为:305,500;五,一,445.
【点评】此题首先根据问题从图中找出所需要的信息,然后根据减法的意义列式计算即可解答.
四.应用题(共10小题)
19.【分析】(1)根据折线统计图可知,跑完1000米,马军用了5分钟,王林用了4分钟,所以王林比赛赢了.;
(2)在起跑后的第1分钟,马军跑了400米,王林大约跑了280米,所以在起跑后的第1分,马军跑的速度快些;在起跑后的第3分钟,两人的折线相重合,此时两人跑的路程同样多,大约是800米;
(3)根据公式路程÷时间=速度进行计算即可得到答案.
【解答】解:(1)跑完1000米,马军用了5分钟,王林比赛赢了.
(2)起跑后的第1分钟,马军速度快一些.第3分钟,两人跑的路程相同,是800米.
(3)1000÷4=250(米/分)
答:王林的平均速度是250米/分.
故答案为:5,王林,马军,3,800,250.
【点评】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行分析、计算即可.
20.【分析】(1)这两条线的交点就是两车相遇地点.由图知两车开出4.4小时后相遇;
(2)开出4小时后货车距离A地由500千米变为200千米,因此可以求出货车每小时行多少千米;
(3)2小时至3小时客车行驶路线是水平的,说明处于停留阶段.停留前后的两条线是平行的,可以得出停留前后速度相同;
(4)由图知,当货车到达A地时,客车距B地还有220千米,据此求出它到B地还需的时间;
(5)根据“路程÷速度和=相遇时间”做题.
【解答】解:(1)由图知,两车开出4.4小时后相遇.
(2)(500﹣200)÷4=75(千米)
答:货车每小时约行75千米.
(3)500﹣100=400(千米)
3﹣2=1(小时)
答:客车在距B地400千米的地方停留了1小时,由图知停留前后的速度相同.
(4)由图知,当货车到达A地时,客车距B地还有220千米.
220÷50=4.4(小时)
答:按照它的行驶速度,到B地还需4.4小时.
(5)500÷(50+75)=4(小时)
答:假如客车不在途中停留,两车开出4小时后就能相遇.
【点评】做这类题关键要学会根据图形分析问题,实线代表客车行驶情况,虚线代表货车行驶情况,这两条线的交点就是两车相遇地点,2小时至3小时客车行驶路线是水平的,说明处于停留阶段,然后结合图形依次做题.
21.【分析】(1)根据图示可知,从9:00到9:30小刚在公园游玩,所以他玩的时间为:9:30﹣9:00=30分钟;
(2)根据图示可知,小刚从8:00到8:20骑车行驶了3千米的路程,所以其速度为:8:20﹣8:00=20分钟,3÷20=(千米/分);所以小刚到达公园所需时间为:6=40(分钟),8:00+40分钟=8:40.
【解答】解:(1)9:30﹣9:00=30分钟
答:小刚在公园玩了30分钟.
(2)8:20﹣8:00=20分钟
3÷20=320(千米/分)
6÷320=40(分钟)
8:00+40分钟=8:40
答:不休息,他8:40可以到达公园.
【点评】本题主要考查单式折线统计图的应用,关键从统计图中找到解决问题的条件,解决问题.
22.【分析】(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)通过观察统计图可知,产值最高的是5月份,根据求一个数比另一个数多几,用减法解答.
(3)根据求平均数的方法,用第一季度的总产值除以3即可就是第一季度平均每月的产值,该厂的每月产值是呈上升趋势.
(4)折线统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.据此解答.
【解答】解:(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)40﹣35=5(万元)
答:产值最高的是5月份,5月份的产值比4月份的产值增加了5万元.
(3)(5+15+22)÷3
=42÷3
=14(万元)
答:该厂第一季度平均每月的产值是14万元,厂的每月产值是呈上升趋势.
(4)这种统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
故答案为:折线、月份、产值、5万元;5、5;14、上升.不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.【分析】(1)由复式折线统计图可以看出:第二场比赛中,一中得48份,二中得53分,用二中所得的分数减一中所得的分数.
(2)第一由复式折线统计图即可看出,第四场表示一中、二中分数的占之间的距离最大,说明此场比赛两个学校的篮球队成绩相差最大.
【解答】解:(1)53﹣48=5(分)
答:两个学校的篮球队第二场比赛时成绩相差5分.
(2)第四场比赛两个学校的篮球队成绩相差最大.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
24.【分析】(1)根据速度=路程÷时间,求出分别求出前5分乌龟和兔子的速度各多少米,再根据时间=路程÷速度,分别求出兔子、乌龟各用多少分钟到达终点,然后根据求一个数比另一个数多或少几,用减法解答.
(2)兔子睡了33﹣5=28分钟,乌龟比兔子早到35﹣30=5分钟,据此解答即可.
【解答】解:(1)200÷5=40(米/分)
40÷5=8(米/分)
280÷8﹣280÷40
=35﹣7
=28(分钟)
答:兔子的速度是每分钟跑40米,乌龟的速度是每分钟爬8米,按这样的速度,兔子应比乌龟早到24分钟.
(2)33﹣5=28(分钟)
35﹣30=5(分钟)
答:实际上兔子中途睡了28分钟,乌龟比兔子早到5分钟.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
25.【分析】(1)把30分钟化成0.5小时,2.5小时行驶了200千米,用200除以2.5求出速度,用速度乘0.5小时就是他们出发30分钟时,离家多少千米.
(2)观察图发现,2.5小时前后的速度不相同,用380千米减去200千米求出从2.5小时到4小时这段时间走的路程,然后再除以(4﹣2.5)小时求出这段时间的速度,再用这段时间的速度乘(3﹣2.5)小时求出(3﹣2.5)小时行驶的路程,再用380千米分别减去200千米和(3﹣2.5)小时行驶的路程就是离目的地还有多少千米.
【解答】解:(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米.
(2)(380﹣200)÷(4﹣2.5)×(3﹣2.5)
=180÷1.5×0.5
=60(千米)
380﹣200﹣60
=180﹣60
=120(千米)
答:离目的地还有120千米.
【点评】本题考查了速度、时间与路程关系式的应用,关键是根据2.5小时行驶了200千米求出速度.要注意2.5小时前后的速度不相同.
26.【分析】(1)小华从1时出发到3=3时返回,求从出发到返回一共经过了多长时间就用返回的时间减去出发的时间解答.
(2)返回前,小华在路上用的时间是1小时,在公园里玩的时间是=小时,求多多少分钟用减法解答,再化成分钟即可.
(3)先把时间化成分钟,把路程化成米,再用路程除以返回的时间解答.
【解答】解:(1)3
=3
=(小时)
答:一共经过了2小时.
(2)1﹣
=1﹣
=(小时)
答:返回前,小华在路上用的时间比在公园里玩的时间多20分钟.
(3)小时=小时=40分钟,6千米=6000米
6000÷40=150(米)
答:返回时,小华骑自行车每分钟行走150米.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.要注意单位的统一.
27.【分析】(1)通过观察统计图可知,小丽行车期间的最高车速是60千米/时.
(2)小丽在9:06为躲避那猫而踩刹车.
(3)由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.据此解答.
【解答】解:(
1
)小丽行车期间的最高车速是60千米/时.
(
2
)小丽在9:06为躲避那猫而踩刹车.
(
3
)答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
28.【分析】(1)通过观察统计图可知,2015年两校参加课外活动的人数相差最多,根据求一个数比另一个多或少几,用减法解答.
(2)根据甲校2015年比2014年增加700人,由此可以预测2016年甲校参加课外活动的人数约有2800人;根据乙校2015年比2014年增加250人,由此可以预测2016年乙校参加课外活动的人数约有1500人.
(3)通过观察统计图可知,甲校参加课外活动的人数在2015年上升最多.据此解答.
【解答】解:(1)2000﹣1250=750(人)
答:2015年两校参加课外活动的人数相差最多,相差750人.
(2)根据两校参加课外活动的人数逐年增加的人数,我估计2016年甲校参加课外活动的人数约有2800人;乙校参加课外活动的人数约有1500人.
(3)甲校参加课外活动的人数在2015年上升最多.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
折线统计图》单元测试题
一.选择题(共8小题)
1.某市规定每户用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨水价为3元.下图能表示每月水费与用水量关系的示意图是( )
A.
B.
C.
D.
2.星期天,林林从家出发到书店买故事书,然后回到家里,下面第( )幅图描述的是林林的行为.
A.
B.
C.
3.如图是甜甜从家出发到莲花山公园去玩再返回的图,根据图中的信息,下面说法错误的是( )
A.甜甜家距莲花山公园6千米
B.甜甜在去的路上休息了20分钟
C.甜甜在莲花山公园玩了1小时
D.甜甜返回时的速度是18千米/小时
4.下面事件中,( )最适合用如图来表示.
A.某校六个班的人数
B.某个月中6天的天气情况
C.六个好朋友每天看书时间统计
D.张明近几年的身高情况.
5.妈妈带小华去公园玩.她们从家出发,直接到了公园,然后她们在公园里玩了几小时,在返回的路上买了瓶水后就径直回家了.下面
( )幅图描述的是上面的情景.
A.
B.
C.
6.如图是甲、乙两个城市今年上半年月平均气温统计图,从图中可以看出,乙城市月平均气温高于甲城市的有( )个月.
A.2
B.3
C.4
D.5
7.如图所示的图象表示斑马和长颈鹿的奔跑情况,下面的说法不符合这个图象的是( )
A.斑马奔跑的路程与奔跑的时间成比例
B.长颈鹿25分钟跑了20千米
C.长颈鹿比斑马跑得快
D.斑马跑12千米用了10分钟
8.星期天王叔叔和李叔叔两家自驾车去游玩.两辆车从同一地点同时出发,行至十字路口时,王叔叔的车刚刚驶过,红灯亮起,李叔叔只能停下.绿灯亮起时,李叔叔继续前行追赶王叔叔,结果李叔叔比王叔叔提前到达目的地与上述文字描述相吻合的图是( )
A.
B.
C.
二.填空题(共8小题)
9.根据甲、乙两车的行程图填空.
(1)甲车时速是
千米/时.
(2)甲乙两车时速的差是
千米/时.
(3)甲乙两车速度的比是
.
10.①右图是复式
统计图.
②
月份的收入和支出相差最大.
③收入最高与收入最低的最简整数比是
.
④上半年年平均每月支出
万元.(保留一位小数)
11.
①
车先行完30千米距离.
②乙车比甲车先行
分钟.
③甲车时速是
千米.
④甲、乙两车时速差
千米.
12.下面是某小学2008~2014年患龋齿人数情况统计图,根据统计图回答问题.
(1)男、女生患龋齿人数最多的是
年,一共
人;在
年男生患龋齿的人数最少,
年男、女生患龋齿的人数相差最多,
年男、女生患龋齿的人数同样多.
(2)从总体上看,男、女生患龋齿的人数呈
趋势.女生从
年到
年患龋齿的人数出现了回升,男生患齲齿的人数有
次出现回升.
13.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同.图中反映了小明一天24小时内体温的变化情况,那么小明一天中的体温从
时到
时一直在升高.
14.“小明和爸爸一起出门去散步,走到街心花园,小刚遇见了小红,两人玩了一会儿后,小明回家做作业了,爸爸看他们玩了一会儿后向远处的超市走去.”下面图
正确描述了小明的行为,图
正确描述了爸爸的行为.
15.某服装厂一、二车间产值情况统计如图.
(1)纵轴上每个单位长度表示
万元.
(2)一车间平均每季度产值
万元,二车间平均每季度产值
万元.
(3)第二季度一车间产值比二车间多
万元,二车间第三季度产值比第二季度多
万元.
16.下面的图象表示甲乙两辆汽车行驶的时间和路程.
(1)行驶12千米甲汽车比乙汽车大约少用
分.
(2)按这样的速度,行驶500千米,甲汽车要行驶
小时,乙汽车要行驶
小时.
三.操作题(共2小题)
17.如图是某便利店两种品牌的纯牛奶1﹣6月销售情况统计表.
月份
1
2
3
4
5
6
销量
甲
20
25
35
40
50
55
乙
15
18
20
16
12
10
请制成复式折线统计图,并回答问题:
(1)你了解到哪些信息?
(2)如果你是便利店经理,下月你准备怎样进货?为什么?
18.下面是明德小学2014年一~六年级植树情况统计图.
①二年级植树的棵数是
棵,六年级植树的棵数是
棵.
②植树最多的年级是
年级,植树最少的年级是
,它们相差
棵.
四.应用题(共10小题)
19.王林和马军参加1000米的长跑比赛,下图中的两条折线分别表示两人在途中的情况,看图回答问题.
(1)跑完1000米,马军用了
分钟,
(填姓名)比赛赢了.
(2)起跑后的第1分钟,
速度快一些.第
分钟,两人跑的路程相同,是
米.
(3)王林的平均速度是
米/分.
20.客车从A地开往B地,货车从B地开往A地,它们行驶的情况如图.
(1)观察如图,两车开出多少小时后相遇?
(2)货车每小时约行多少千米?
(3)客车在距B地多少千米的地方停留了多长时间?停留前后的速度相同吗?
(4)估一估:当货车到达A地时,客车距B地还有多少千米?按照它的行驶速度,到B地还需多少小时?
(5)假若客车不在途中停留,请你用你喜欢的方法求出两车开出多少小时后就能相遇.
21.小刚骑车到离家6千米的一个公园游玩.根据折线图解答下列问题.
(1)小刚在公园玩了多长时间?
(2)如果一直骑车,不休息,他什么时候可以到达公园?
22.振兴玩具厂1~5月的产值如图所示.
(1)这是一幅
统计图,横轴表示
,纵轴表示
,每格代表
.
(2)产值最高的是
月,5月的产值比4月的产值增加了
万元.
(3)该厂第一季度平均每月的产值是
.该厂的每月产值是呈
趋势.(填“上升”或“下降”)
(4)这种统计图的优点是
.
23.下面是某市一中和二中篮球队的五场比赛得分情况统计图.
(1)两个学校的篮球队第二场比赛时成绩相差多少分?
(2)哪场比赛两个学校的篮球队成绩相差最大?
24.如图的折线图表示的是乌龟和兔子赛跑时路程和时间的关系.
(1)前5分乌龟和兔子的速度各是多少?按这样的速度,兔子应比乌龟早到几分?
(2)实际上兔子中途睡了几分?乌龟比兔子早到几分?
25.国庆节期间,王老师一家自驾游去了离家380千米的某地,右面是他们离家的距离y(千米)与汽车行驶时间x(时)之间的关系图.
(1)他们出发30分钟时,离家多少千米?
(2)他们出发3小时时,离目的地还有多少千米?
26.如图是小华骑自行车到6千米远的森林公园去游玩的情况.
(1)小华从出发到返回,一共经过了多长时间?
(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?
(3)返回时,小华骑自行车每分钟行走多少米?
27.小丽驱车外出兜风,半途中突然有一只猫冲到车前,她用力刹车才没撞到它.小丽受惊后决定开车回家.以下的折线图是小丽行车的速度记录.
(1)小丽行车期间的最高车速是多少?
(2)小丽在什么时间为躲避那猫而踩刹车?
(3)由如图的数据,能否知道小丽回程的路线,是不是比她从家里出发到发生此意外事件的路线距离短?请解释你的答案.
28.某市甲,乙两所学校学生参加课外活动情况统计图如下.
(1)哪﹣年两校参加课外活动的人数相差最多?相差多少人?
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有多少人,乙校参加课外活动的有多少人?
(3)甲校参加课外活动的人数在哪个时间段上升最多?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】由题意可知:每户每月用水量不超过10吨,每吨价格为2.5元;即10吨以内,每吨水的单价变化不大,然后水量超过10吨时,超过部分每吨价格为3元,单价变化相对来说幅度变大;据此选择即可
【解答】解:由分析知:每户每月用水量不超过10吨,每吨价格为2.5元;当用水量超过10吨时,超过部分每吨价格为3元.下面4幅图中能表示每月水费与用水量关系的是C;
故选:C.
【点评】此题应根据单价和用水吨数之间的关系进行判断.
2.【分析】根据题意,结合图示,图A表明小明从家出发后有折回家中,然后再从家出发到达书店停留了一会就再次返回家中,符合题意;图B显然不正确,没有在书店停留的时间;图C显示不正确,出发地点不是从家出发;据此解答.
【解答】解:A:表明小明从家出发后有折回家中,然后再从家出发到达书店停留了一会就再次返回家中,符合题意;
B:没有在书店停留的时间,所以此描述错误;
C:出发地点不是从家出发;所以不正确.
所以,图A比较准确地描述了上面的情景.
故选:A.
【点评】此题为一次折线图象与实际结合的题型,同学们要培养从图形中找信息的能力.
3.【分析】根据图象分析出甜甜从家出发到莲花山公园去玩再返回的家的过程,进而判断即可.
【解答】解:由折线统计图可以看出,纵轴上数据表示路程,单位是千米,每格代表1千米,甜甜家到莲花山公园相距6格,即6千米,所以A说法正确;
根据图示可以看出甜甜从家出发到莲花山公园的路上休息了20分钟,所以B说法正确;
10时到达莲花山公园,10时40分开始回家,所以在莲花山公园玩了40分钟,不是玩了1小时,所以C说法错误;
用路程除以甜甜返回用的时间就是甜甜返回时速度,6÷=18(千米),所以D计算正确;
故选:C.
【点评】本题主要考查了学生能正确根据折线统计图发现问题并解决问题的能力.
4.【分析】根据折线统计图的特点及作用,折线统计图不仅能表示数量的多少,而且能反映出数量之间的增减变化的趋势.
【解答】解:A,表示某校六个班的人数,选用条形统计图;
B,表示某个月中6天的天气情况,选用条形统计图;
C,表示六个好朋友每天看书的时间统计,选用折线统计图;
D,表示张明近几年的身高情况,选用折线统计图;但是它的身高是逐渐增高,而不是下降.所以此图不符合张明近几年的身高情况.
因此,以上事件能用此图表示的是六个好朋友每天看书的时间统计.
故选:C.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用.
5.【分析】根据运动的路程与时间判断折线图象.注意几个行走段:“她们从家出发,直接到了公园”此时的折线应呈上升趋势,“她们在公园里玩了几小时”此时的折线应处于持平,“在返回的路上买了瓶水后就径直回家了”此时的折线应处于小幅度的持平然后再下降.
【解答】解:A:表示小华和妈妈从家出发直接到公园后没有停留,而在返回途中停留的时间较长(买水),最后买完水后直接回家,因为没有表示出在公园的停留时间,所以错误;
B:根据图示,第一处停留表示在公园里玩耍,第二处停留表示买水,图B表示玩耍的时间小于买水的时间,所以此描述错误;
C:根据图示,第一处停留表示在公园里玩耍,第二处停留表示买水,图C表示玩耍的时间大于买水的时间,所以图C描述正确;
故选:C.
【点评】此题为一次折线图象与实际结合的题型,同学们要培养从图形中找信息的能力.
6.【分析】通过观察折线统计图可知,乙城市的月平均气温高于甲城市的月平均气温有3月和4月。据此解答。
【解答】解:乙城市的月平均气温高于甲城市的月平均气温有3月和4月。
答:乙城市月平均气温高于甲城市的有2个月。
故选:A。
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
7.【分析】根据图象对各选项进行依次分析、进而得出结论.
【解答】解:A、因为12÷10=1.2千米,24÷20=1.2千米,…,即斑马奔跑的路程÷奔跑的时间=斑马速度(一定),所以奔跑的路程与奔跑的时间成正比例;
B、由图象可知:长颈鹿25分钟跑了20千米;
C、由图象可知:斑马比长颈鹿跑的快,所以C选项长颈鹿比斑马跑得快,说法错误;
D、由图象可知:斑马跑12千米用了10分钟;
故选:C.
【点评】此题考查了学生根据统计图获取信息的能力,能够根据图象提出问题并能解决问题的能力.
8.【分析】根据题意和各个统计图中的图象,可以判断出哪个统计图中的图象与题目中的文字描述相吻合.
【解答】解:A统计图符合题意;
B统计图中李叔叔到达终点晚于王叔叔,与题目中果李叔叔比王叔叔提前到达目的地矛盾,故选项B不符合题意;
C统计图中刚开始李叔叔比王叔叔行驶的快,与题干中两辆车从同一地点同时出发,行至十字路口时,王叔叔的车刚刚驶过,红灯亮起,李叔叔只能停下矛盾,故选项C不符合题意;
故选:A.
【点评】此题主要考查复式折线统计图,明确题意,可以判断出哪个选项中的图象与题目中的文字吻合是解答本题的关键.
二.填空题(共8小题)
9.【分析】(1)甲车在1小时20分钟内行驶了30千米,可根据公式:路程÷时间=速度进行计算即可得到答案;
(2)乙车在1小时40分钟的时间内行驶了30千米,根据公式计算出乙车行驶的速度,然后再用甲车的速度减去乙车的速度即可得到答案;
(3)可用路程÷时间=速度分别计算出甲乙的速度,然后再比用甲、乙两车的速度相比即可.
【解答】解:(1)1时20分钟=1小时
30÷1=22.5(千米)
答:甲车时速22.5千米.
(2)1时40分钟=1小时,
乙车的速度为:30÷1=18(千米),
甲乙两车时速之差是:22.5﹣18=4.5(千米),
答:甲乙两车时速之差是4.5千米;
(3)22.5:4.5=(22.5÷4.5):(4.5÷4.5)=5:1
答:甲乙两车速度的比是
5:1.
故答案为:(1)22.5,(2)4.5,(3)5:1
【点评】此题主要考查的是如何从统计图中获取信息,然后再根据所得到的信息进行计算即可,此题主要用到的公式是速度=路程÷时间.
10.【分析】①观察可知,此图为复式折线统计图;
②通过观察统计图,可知7月份的收入和支出相差最大;
③收入最高的是11月份,是90万元;收入最低的是3和4月份,都是30万元,进而写出收入最高与收入最低的整数比,再根据比的性质化成最简比;
④用上半年,即1﹣6月份的总支出除以月份数6即可.
【解答】解:①右图是复式
折线统计图;
②7月份的收入和支出相差最大;
③收入最高与收入最低的比是:90:30=3:1;
④(20+30+10+20+20+30)÷6,
=130÷6,
≈21.7(万元);
答:上半年年平均每月支出
21.7万元.
故答案为:折线,7,3:1,21.7.
【点评】此题主要考查的是如何观察复式折线统计图,并从统计图中获取有用的信息,进行分析、解决问题.
11.【分析】①观察统计图,可知甲车行完30千米距离时的时刻是3:40,而乙车行完30千米距离时的时刻是4:00,所以甲车先行完的30千米距离;
②甲车开始行驶的时刻是2:40,乙车开始行驶的时刻是2:00,用2:40减去2:00,就是乙车比甲车先行的时间;
③甲车开始行驶的时刻是2:40,行完30千米的时刻是3:40,先求出甲车行驶的时间,进而根据路程÷时间=速度求出甲车的时速;
④乙车开始行驶的时刻是2:00,行完30千米的时刻是4:00,先求出乙车行驶的时间,进而根据路程÷时间=速度求出甲车的时速,再求得甲、乙两车时速差.
【解答】解:①根据分析,可知甲车先行完的30千米距离;
②2时40分﹣2时=40分.
答:乙车比甲车先行40分钟.
③3时40分﹣2时40分=1小时
30÷1=30(千米).
答:甲车时速是309千米.
④4时﹣2时=2小时
30÷2=15(千米)
30﹣15=15(千米).
答:甲、乙两车时速差15千米.
故答案为:甲,40,30,15.
【点评】此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法.
12.【分析】(1)找出这两条线的最高点,就是这一年男生、女生患龋齿的人数最多的年份,即2008年,然后再把人数相加,即86+81=167人;
找出这实线的最低点,就是男生患龋齿的人数最少的年份,即2013年;
找出这两条线的差距最大的点,就是男、女生患龋齿的人数相差最多的年份,即2013年;
找出这两条线的差距相交的点,就是男、女生患龋齿的人数同样多的年份,即2012年;
(2)根据折线的总体变化趋势,从总体上看,男、女生患龋齿的人数呈下降趋势.女生从2011年到2012年患龋齿的人数出现了回升,男生患齲齿的人数有2次出现回升.据此解答.
【解答】解:(1)男、女生患龋齿人数最多的是2008年,一共167人;在2013年男生患龋齿的人数最少,2013年男、女生患龋齿的人数相差最多,2012年男、女生患龋齿的人数同样多.
(2)从总体上看,男、女生患龋齿的人数呈下降趋势.女生从2011年到2012年患龋齿的人数出现了回升,男生患齲齿的人数有2次出现回升.
故答案为:2008,167,2013,2013,2012;下降,2011,2012,2.
【点评】本题主要考查了如何从折线统计图读出数据,以及判断变化趋势,根据问题选择合适的数据进行解答.
13.【分析】分析折线统计图,折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,从5时到17时,小明的体温一直是升高的趋势,从而可求出答案.
【解答】解:由折线统计图可知:折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,则小明这一天的体温范围是36.5≤T≤37.5;从5时到17时,小明的体温一直是升高的趋势,而17﹣24时的体温是下降的趋势.
所以那么小明一天中的体温从
5时到
17时一直在升高.
故答案为:5,17.
【点评】读懂统计图,从图中得到必要的信息是解决本题的关键.
14.【分析】由于小明和爸爸一起去散步,从家到街心花园,小明遇见了小红,两人玩了一会儿后,小明回家做作业了,用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;爸爸看他们玩了一会儿后向远处的超市走去,用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远,据此解答.
【解答】解:小明用图来表示应是小明离家的距离逐渐变远,然后同小红玩时的距离固定,然后再离家变近;
爸爸用图来表示应是爸爸离家的距离逐渐变远,然后看小时同小红玩时的距离固定,然后再离家变远.
故选:C,B.
【点评】本题是一个信息题目,主要利用图象信息找到所需要的数量关系,然后利用这些关系即可确定图象.
15.【分析】(1)通过观察统计图可知,纵轴上每个单位长度表示100万元.
(2)根据求平均数的方法,先分别求出一车间、二车间全年的总产值,然后分别除以4即可.
(3)根据求一个数比另一个数多几,用减法解答.
【解答】解:(1)纵轴上每个单位长度表示100万元.
(2)(250+360+510+340)÷4
=1460÷4
=365(万元)
(200+250+300+230)÷4
=980÷4
=245(万元)
答:一车间平均每季度产值是365万元,二车间平均每季度产值是245万元.
(3)360﹣250=110(万元)
300﹣250=50(万元)
答:第二季度一车间产值比二车间多110万元,二车间第三季度产值比第二季度多50万元.
故答案为:100;365、245;110、50,.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
16.【分析】(1)找出路程是12千米时,甲、乙两汽车的直线图上对应的时间,两时间的差就是答案;
(2)利用路程÷时间=速度分别计算出甲乙两车的行驶速度,然后再用500千米分别除以甲乙两车的速度即可得到需要行驶的时间.
【解答】解:(1)12﹣6=6(分)
答:行驶12千米甲汽车比乙汽车大约少用
6分;
(2)甲车:500÷(16÷8)
=500÷2
=250(分钟)
≈4.17(小时)
乙车:500÷(12÷12)
=500÷1
=500(分钟)
≈8.33(小时)
答:甲汽车要行驶
4.17小时,乙汽车要行驶
8.33小时.
故答案为:6,4.17、8.33.
【点评】解答此图的关键是,会看懂此表,根据速度,路程,时间的关系,找出数量关系,找准对应量,列式解答即可.
三.操作题(共2小题)
17.【分析】首先根据数据描出各点,再顺次连接即可.
(1)了解到甲品牌的销售量越来越多,乙品牌的销售量越来越少.
(2)如果是便利店经理,下月准备多进一些甲品牌的纯牛奶,因为甲品牌的销售量越来越多.
【解答】解:画图如下,
(1)了解到甲品牌的销售量越来越多,乙品牌的销售量越来越少.
(2)如果是便利店经理,下月准备多进一些甲品牌的纯牛奶,因为甲品牌的销售量越来越多.
【点评】此题主要考查了统计图表的填补,以及从统计图表中获取信息的能力,要熟练掌握.
18.【分析】①根据统计图中的数据判断解答.
②植树最多的是五年级,植树最少的是一年级,用五年级植树的棵数减去一年级植树的棵数就是相差的棵数.
【解答】解:①二年级植树的棵数是305棵,六年级植树的棵数是500棵.
②645﹣200=445(棵)
答:植树最多的年级是五年级,植树最少的年级是一年级,它们相差445棵.
故答案为:305,500;五,一,445.
【点评】此题首先根据问题从图中找出所需要的信息,然后根据减法的意义列式计算即可解答.
四.应用题(共10小题)
19.【分析】(1)根据折线统计图可知,跑完1000米,马军用了5分钟,王林用了4分钟,所以王林比赛赢了.;
(2)在起跑后的第1分钟,马军跑了400米,王林大约跑了280米,所以在起跑后的第1分,马军跑的速度快些;在起跑后的第3分钟,两人的折线相重合,此时两人跑的路程同样多,大约是800米;
(3)根据公式路程÷时间=速度进行计算即可得到答案.
【解答】解:(1)跑完1000米,马军用了5分钟,王林比赛赢了.
(2)起跑后的第1分钟,马军速度快一些.第3分钟,两人跑的路程相同,是800米.
(3)1000÷4=250(米/分)
答:王林的平均速度是250米/分.
故答案为:5,王林,马军,3,800,250.
【点评】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行分析、计算即可.
20.【分析】(1)这两条线的交点就是两车相遇地点.由图知两车开出4.4小时后相遇;
(2)开出4小时后货车距离A地由500千米变为200千米,因此可以求出货车每小时行多少千米;
(3)2小时至3小时客车行驶路线是水平的,说明处于停留阶段.停留前后的两条线是平行的,可以得出停留前后速度相同;
(4)由图知,当货车到达A地时,客车距B地还有220千米,据此求出它到B地还需的时间;
(5)根据“路程÷速度和=相遇时间”做题.
【解答】解:(1)由图知,两车开出4.4小时后相遇.
(2)(500﹣200)÷4=75(千米)
答:货车每小时约行75千米.
(3)500﹣100=400(千米)
3﹣2=1(小时)
答:客车在距B地400千米的地方停留了1小时,由图知停留前后的速度相同.
(4)由图知,当货车到达A地时,客车距B地还有220千米.
220÷50=4.4(小时)
答:按照它的行驶速度,到B地还需4.4小时.
(5)500÷(50+75)=4(小时)
答:假如客车不在途中停留,两车开出4小时后就能相遇.
【点评】做这类题关键要学会根据图形分析问题,实线代表客车行驶情况,虚线代表货车行驶情况,这两条线的交点就是两车相遇地点,2小时至3小时客车行驶路线是水平的,说明处于停留阶段,然后结合图形依次做题.
21.【分析】(1)根据图示可知,从9:00到9:30小刚在公园游玩,所以他玩的时间为:9:30﹣9:00=30分钟;
(2)根据图示可知,小刚从8:00到8:20骑车行驶了3千米的路程,所以其速度为:8:20﹣8:00=20分钟,3÷20=(千米/分);所以小刚到达公园所需时间为:6=40(分钟),8:00+40分钟=8:40.
【解答】解:(1)9:30﹣9:00=30分钟
答:小刚在公园玩了30分钟.
(2)8:20﹣8:00=20分钟
3÷20=320(千米/分)
6÷320=40(分钟)
8:00+40分钟=8:40
答:不休息,他8:40可以到达公园.
【点评】本题主要考查单式折线统计图的应用,关键从统计图中找到解决问题的条件,解决问题.
22.【分析】(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)通过观察统计图可知,产值最高的是5月份,根据求一个数比另一个数多几,用减法解答.
(3)根据求平均数的方法,用第一季度的总产值除以3即可就是第一季度平均每月的产值,该厂的每月产值是呈上升趋势.
(4)折线统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.据此解答.
【解答】解:(1)这是一幅折线统计图,横轴表示月份,纵轴表示产值,每格代表5万元.
(2)40﹣35=5(万元)
答:产值最高的是5月份,5月份的产值比4月份的产值增加了5万元.
(3)(5+15+22)÷3
=42÷3
=14(万元)
答:该厂第一季度平均每月的产值是14万元,厂的每月产值是呈上升趋势.
(4)这种统计图的优点是:不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
故答案为:折线、月份、产值、5万元;5、5;14、上升.不仅能够反映数量的多少,而且能够反映数量增减变化的趋势.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.【分析】(1)由复式折线统计图可以看出:第二场比赛中,一中得48份,二中得53分,用二中所得的分数减一中所得的分数.
(2)第一由复式折线统计图即可看出,第四场表示一中、二中分数的占之间的距离最大,说明此场比赛两个学校的篮球队成绩相差最大.
【解答】解:(1)53﹣48=5(分)
答:两个学校的篮球队第二场比赛时成绩相差5分.
(2)第四场比赛两个学校的篮球队成绩相差最大.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
24.【分析】(1)根据速度=路程÷时间,求出分别求出前5分乌龟和兔子的速度各多少米,再根据时间=路程÷速度,分别求出兔子、乌龟各用多少分钟到达终点,然后根据求一个数比另一个数多或少几,用减法解答.
(2)兔子睡了33﹣5=28分钟,乌龟比兔子早到35﹣30=5分钟,据此解答即可.
【解答】解:(1)200÷5=40(米/分)
40÷5=8(米/分)
280÷8﹣280÷40
=35﹣7
=28(分钟)
答:兔子的速度是每分钟跑40米,乌龟的速度是每分钟爬8米,按这样的速度,兔子应比乌龟早到24分钟.
(2)33﹣5=28(分钟)
35﹣30=5(分钟)
答:实际上兔子中途睡了28分钟,乌龟比兔子早到5分钟.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
25.【分析】(1)把30分钟化成0.5小时,2.5小时行驶了200千米,用200除以2.5求出速度,用速度乘0.5小时就是他们出发30分钟时,离家多少千米.
(2)观察图发现,2.5小时前后的速度不相同,用380千米减去200千米求出从2.5小时到4小时这段时间走的路程,然后再除以(4﹣2.5)小时求出这段时间的速度,再用这段时间的速度乘(3﹣2.5)小时求出(3﹣2.5)小时行驶的路程,再用380千米分别减去200千米和(3﹣2.5)小时行驶的路程就是离目的地还有多少千米.
【解答】解:(1)30分钟=0.5小时
200÷2.5=80(千米)
80×0.5=40(千米)
答:他们出发30分钟时,离家40千米.
(2)(380﹣200)÷(4﹣2.5)×(3﹣2.5)
=180÷1.5×0.5
=60(千米)
380﹣200﹣60
=180﹣60
=120(千米)
答:离目的地还有120千米.
【点评】本题考查了速度、时间与路程关系式的应用,关键是根据2.5小时行驶了200千米求出速度.要注意2.5小时前后的速度不相同.
26.【分析】(1)小华从1时出发到3=3时返回,求从出发到返回一共经过了多长时间就用返回的时间减去出发的时间解答.
(2)返回前,小华在路上用的时间是1小时,在公园里玩的时间是=小时,求多多少分钟用减法解答,再化成分钟即可.
(3)先把时间化成分钟,把路程化成米,再用路程除以返回的时间解答.
【解答】解:(1)3
=3
=(小时)
答:一共经过了2小时.
(2)1﹣
=1﹣
=(小时)
答:返回前,小华在路上用的时间比在公园里玩的时间多20分钟.
(3)小时=小时=40分钟,6千米=6000米
6000÷40=150(米)
答:返回时,小华骑自行车每分钟行走150米.
【点评】解答本题的关键是能从统计图中获取与问题有关的信息,再根据基本的数量关系解决问题.要注意单位的统一.
27.【分析】(1)通过观察统计图可知,小丽行车期间的最高车速是60千米/时.
(2)小丽在9:06为躲避那猫而踩刹车.
(3)由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.据此解答.
【解答】解:(
1
)小丽行车期间的最高车速是60千米/时.
(
2
)小丽在9:06为躲避那猫而踩刹车.
(
3
)答:由图中的数据,可以知道小丽回程的路线比她从家里出发到发生此意外事件的路线距离短.因为小丽从家里出发到发生意外事件时用了6分钟,回程时到发生意外事件时虽然也用了6分钟,虽然都用最高速度行了4分钟,但是回程时的最高速度只有36千米/时行了4分钟,而出发时用最高速度60千米/时却行了4分钟.用的时间虽然相同,但回程时的速度却很慢,所以回程时的路线短.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
28.【分析】(1)通过观察统计图可知,2015年两校参加课外活动的人数相差最多,根据求一个数比另一个多或少几,用减法解答.
(2)根据甲校2015年比2014年增加700人,由此可以预测2016年甲校参加课外活动的人数约有2800人;根据乙校2015年比2014年增加250人,由此可以预测2016年乙校参加课外活动的人数约有1500人.
(3)通过观察统计图可知,甲校参加课外活动的人数在2015年上升最多.据此解答.
【解答】解:(1)2000﹣1250=750(人)
答:2015年两校参加课外活动的人数相差最多,相差750人.
(2)根据两校参加课外活动的人数逐年增加的人数,我估计2016年甲校参加课外活动的人数约有2800人;乙校参加课外活动的人数约有1500人.
(3)甲校参加课外活动的人数在2015年上升最多.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
