2020-2021学年人教版五年级数学下册《第七章 折线统计图》单元测试题(含解析)
文档属性
| 名称 | 2020-2021学年人教版五年级数学下册《第七章 折线统计图》单元测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 564.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 19:51:55 | ||
图片预览

文档简介
2020-2021学年人教版五年级数学下册《第七章
折线统计图》单元测试题
一.选择题(共8小题)
1.星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(分)之间的关系.依据统计图,下面描述符合小红散步情景的是( )
A.从家里出发,到一个公共阅报亭看了一会儿报,就回家了
B.从家出发,到了一个公共阅报亭看了一会儿报后,继续向前走了一段,然后回家了
C.从家出发,一直散步(没有停留),然后回来了
D.从家出发,散了一会儿步,就找同学去了,l8分钟后才开始返回
2.华侨商场有四层楼.小红开始在三楼买了点心,再到二楼买了学习用品,又上到四楼买衣服,最后回到一楼买了玩具.比较准确地描述这件事是( )
A.
B.
C.
D.
3.早晨张爷爷步行20分到离家1500米的广场锻炼身体,1时后,张爷爷步行20分回家吃饭,( )反映了张爷爷这一活动行程.
A.
B.
C.
D.
4.如下图,反映室内温度变化情况正确的折线统计图是( )
A.
B.
C.
5.一脚踢出去的足球,反映它的高度与时间的关系是图中( )
A.
B.
C.
D.
6.对复式折线统计图的优点描述最准确的是( )
A.能看出数量的多少
B.可以看出数量的增减变化
C.折线较多,很美观
D.不仅能看出数量的多少和增减变化的情况,而且方便对两组相关数据进行比较
7.一只兔子和一条小狗从同一地点出发,同时开始向东运动,兔子的运动距离与时间关系图象如图中实线部分ABCD所示,小狗的运动距离与时间关系图象如图中虚线部分AD所示.则关于该图象下列说法正确的是( )
A.小狗的速度始终比兔子快
B.整个过程中小狗和兔子的平均速度相同
C.图中BC段表明兔子在做匀速直线运动
D.在前4秒内,小狗比兔子跑得快
8.小强跑步的速度是( )
A.先快后慢
B.先慢后快
C.匀速
D.无法确定
二.填空题(共8小题)
9.一次越野赛跑中,当小明跑了1600米时,小刚跑了1300米.小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的关系如图,则这次越野跑的全程为
米.
10.如图,描述的是一位自行车爱好者从家出发去某地及他回到家中,行驶的距离与所用时间的关系,骑车者9时从家出发,15时回到家中,根据这个折线图填空.
(1)骑车者最远时离家是
千米
(2)11时到12时他骑了
千米
(3)他此次出发至最远处时休息了
小时
(4)他回家时骑车的速度是每小时
千米.
11.下面是一辆汽车与一列火车行程图表,根据图解答:
(1)汽车时速是多少千米?列式计算
(2)火车停站时间是多少分钟?列式计算
(3)火车停站后时速比汽车快多少千米?列式计算
(4)汽车比火车早到多少分钟?列式计算
.
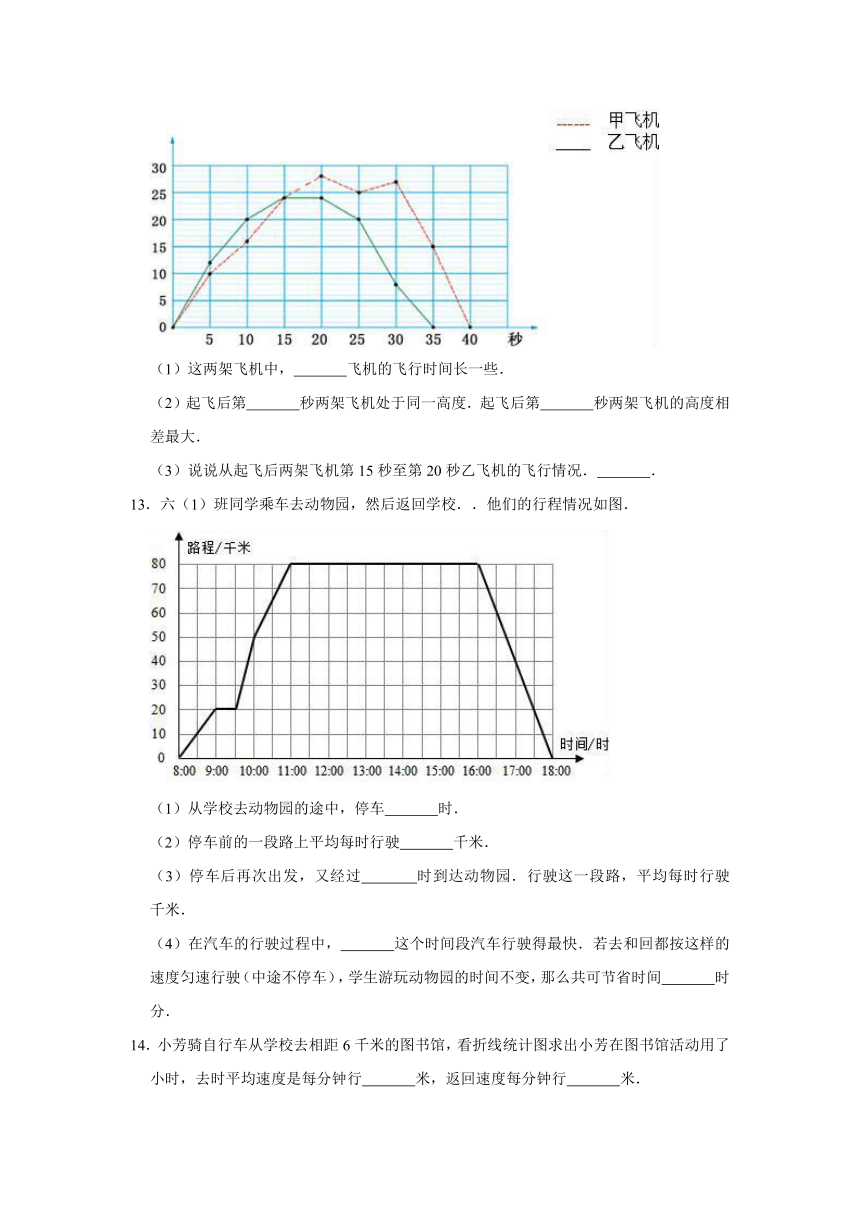
12.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架飞机中,
飞机的飞行时间长一些.
(2)起飞后第
秒两架飞机处于同一高度.起飞后第
秒两架飞机的高度相差最大.
(3)说说从起飞后两架飞机第15秒至第20秒乙飞机的飞行情况.
.
13.六(1)班同学乘车去动物园,然后返回学校..他们的行程情况如图.
(1)从学校去动物园的途中,停车
时.
(2)停车前的一段路上平均每时行驶
千米.
(3)停车后再次出发,又经过
时到达动物园.行驶这一段路,平均每时行驶
千米.
(4)在汽车的行驶过程中,
这个时间段汽车行驶得最快.若去和回都按这样的速度匀速行驶(中途不停车),学生游玩动物园的时间不变,那么共可节省时间
时
分.
14.小芳骑自行车从学校去相距6千米的图书馆,看折线统计图求出小芳在图书馆活动用了
小时,去时平均速度是每分钟行
米,返回速度每分钟行
米.
15.甲、乙两名游泳运动员进行200米游泳比赛,甲让乙先游10秒.赛后,制作了如下的图象.
(1)甲游了
米追上乙.
(2)甲的速度是
米/秒.
16.根据甲、乙两车的行程图填空.
(1)甲车每小时行驶
千米.
(2)甲、乙两车速度的最简整数比是
:
.
(3)甲、乙两车8:00从同一地点出发,同向而行时后,两车相距
千米.
三.操作题(共2小题)
17.某水泥厂第一季度生产情况如下:
1月份计划生产水泥400吨,实际生产450吨;2月份计划生产400吨,实际生产440吨;3月份计划生产水泥500吨,实际生产600吨.
请完成折线统计图.
18.星期天,圆圆随父母去旅游,先游览了A景区,后又游览了B景区.如图是出发后各时刻圆圆离家路程统计图.
(1)他们
时到达A景区,停留了
小时.
时到达B景区,停留了
小时.
(2)B景区离圆圆家的路程是
km.
(3)他们下午
时开始返回,下午
时到家.
四.应用题(共10小题)
19.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
20.如图是某汽车厂两款新车销售情况统计图.
根据图中数据,回答下面的问题.
(1)几月份两款新车的销售量差距最大?
(2)B款车在6个月内一共销售多少辆?平均每个月销售多少辆?
21.一个漏水的水龙头一天要浪费80kg水.(一个月按30天计算)
(1)请你根据计算完成下面的折线统计图.
(2)若100户家庭各有1个水龙头按这样的速度漏水,则这100户家庭一年要浪费多少吨水?
22.小军到离家6km远的奶奶家看望奶奶,请根据折线统计图回答问题.
(1)小军途中一共休息了
次,共
分钟.
(2)小军从家出发到返回家一共用了
小时.
23.如图是某纺织厂2012﹣2015年三、四车间工业产值增长情况统计图.
(1)
车间的工业产值增长较快.
(2)
年两车间的工业产值相差最大.
(3)四车间2015年的工业产值比2014年增长几分之几?
24.某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是
年,从
年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
25.某商场2018年凉鞋的销售情况如图所示.
(1)第一季度共销售
双.
(2)7月份的销售量是5月份的
倍.
(3)图中
月份凉鞋的销售量最高,原因是什么?
(4)这是一幅不完整的折线统计图.请你根据生活实际,完成这幅折线统计图.
26.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
27.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
28.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份
1
2
3
4
5
6
7
8
9
10
11
12
玉溪市
16
18
21
25
27.5
28
27
26.5
26
25
22
17
成都市
4
5
10
16
21
26
29
29
23.5
17.5
11
5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是
月,相差
.
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】根据图象可知,有一段时间内时间在增加,而路程没有增加,意味着有停留,与x轴平行后的函数图象表现为随时间的增多路程又在增加,由此即可作出判断.
【解答】解:从图中看,有一段时间内函数图象与x轴平行,说明时间在增加,而路程没有增加,C、D中没有停留,所以排除C、D.与x轴平行后的函数图象表现为随时间的增多路程又在增加,排除A.
故选:B.
【点评】读懂图象是解决本题的关键.首先应理解函数图象的横轴和纵轴表示的量,再根据函数图象用排除法判断.
2.【分析】根据题意和统计图,因为小红去的楼层各不相同,A显然不正确;B表示先去了4层,因此也不正确;C表示先去三楼,再去二楼,然后去四楼,最后去了一楼,故正确;D表示先去了一楼,因此也不正确.据此解答.
【解答】解:A显然不正确;
B表示先去了4层,因此也不正确;
C表示先去三楼,再去二楼,然后去四楼,最后去了一楼,故正确;
D表示先去了一楼,因此也不正确.
故选:C.
【点评】此题先理解题意,再分析统计图,考查了学生分析统计图的能力.
3.【分析】根据题意可知,张爷爷步行从0分钟到20分钟处于行驶状态折线统计图中的折线应是上升状态,20分钟后到达广场锻炼身体,直到20+60=80分钟有开始步行回家,所以在20分钟到80分钟之间折线处于持平状态,在80分钟到100分钟之间张爷爷开始返回家中,所以折线图应是下降状态,根据分析进行选择即可得到答案.
【解答】解:A、由图可知,在20分钟到80分钟之间折线处于持平状态;
B、由图可知,在20分钟到40分钟折线处于持平状态,在40分钟后到60分钟折线又处于持平状态;
C、折线直接从20分钟开始直线上升,没有匀速行驶的过程;
D、折线从40分钟到80分钟之间处于持平状态,锻炼时间为80﹣40=40分钟.
所以选项A反映了张爷爷这一活动行程.
故选:A.
【点评】解决关键是观察统计图,弄清楚横轴和纵轴分别表示什么量,进而根据折线情况解答问题
4.【分析】根据以上折线统计图的数据,一天中13时的气温达到一天中的最高值,由此判断折线统计图C正确.
【解答】解:一天中13时的气温达到一天中的最高值,
所以反映室内温度变化情况正确的折线统计图是C.
故选:C.
【点评】此题主要考查折线统计图的特点,并能根据它的特点解决有关的实际问题.
5.【分析】根据提出的足球应该是首先上升再下降过程,得出符合要求图象即可.
【解答】解:根据一脚踢出去的球的高度与时间的关系,应该是首先上升再下降过程,所以只有A符合要求.
故选:A.
【点评】解答此题的关键是弄清足球开始和最后与地面的距离为0.
6.【分析】根据三种统计图的优点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答即可.
【解答】解:答:对复式折线统计图的优点描述最准确的是不仅能看出数量的多少和增减变化的情况,而且方便对两组相关数据进行比较.
故选:D.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用.
7.【分析】由图象可以看出:在前4秒,兔子在相同时间内通过的路程比小狗的路程多,所以兔子的运动速度大于小狗的运动速度(由此判断选项D错误);在第4秒,小狗和兔子在相同时间内通过相同的路程,所以它们的平均速度相同;在4到8秒的时间段,小狗在相同时间内通过的路程比兔子的路程多,所以小狗的运动速度大于兔子的运动速度.整个过程中,小狗和兔子运动路程相同,运动时间相同,所以它们的平均速度相同,选项A是错误的,B正确.另,图中的BC段表示兔子处于静止状态.
【解答】解:由分析得:在前4秒,兔子在相同时间内通过的路程比小狗的路程多,所以兔子的运动速度大于小狗的运动速度.由此判断选项A和D错误;
在第4秒,图中的BC段表示兔子处于静止状态,由此判断选项C是错误的;
在4到8秒的时间段,小狗在相同时间内通过的路程比兔子的路程多,所以小狗的运动速度大于兔子的运动速度.整个过程中,小狗和兔子运动路程相同,运动时间相同,所以它们的平均速度相同,选项B正确.
故选:B.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息作出判断和预测.
8.【分析】由表示小强、小刚跑步的折线可以看出:小刚先比小强跑得快,到3分半时,被小强追上反超,从此比小强跑得慢,即先快后慢,最终跑完用时比小强多;小强先比小刚慢,到3分半时追上小刚,并且一直领先,表示小强跑得速度的折线几乎是直线,说明小强几乎是匀速跑的.
【解答】解:如图
小强跑步的速度是匀速.
故选:C.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
二.填空题(共8小题)
9.【分析】设小明的速度为a米/秒,小刚的速度为b米/秒,根据统计图,由行程问题的数量关系建立方程组:,求出其解,进而解决问题.
【解答】解:设小明的速度为a米/秒,小刚的速度为b米/秒,由题意,得:
,
②﹣①得:b=2a,
把b=2a代入①得:a=3,
则b=2×3=6,
所以,
所以这次越野跑的全程为:
1600+300×3
=1600+900
=2500(米).
答:这次越野跑的全程为2500米.
故答案为:2500.
【点评】本题考查了行程问题的数量关系的运用,由统计图的数量关系建立方程组是解答的关键.
10.【分析】(1)由统计图可知:观骑车者最远时离家是30千米;
(2)11时到12时他骑了30﹣15=15千米;
察函数图象得到E点表示离家最远,然后读出E点坐标可得到离家最远的时间与离家的距离;
(3)他此次出发至最远处时休息了13时﹣12时=1小时;
(4)根据速度=路程÷时间进行解答即可.
【解答】解:(1)由统计图可知:观骑车者最远时离家是30千米;
(2)30﹣15=15(千米);
答:11时到12时他骑了15千米.
(3)13时﹣12时=1小时;
答:他此次出发至最远处时休息了1小时.
(4)30÷(15﹣13)
=30÷2
=15(千米);
答:他回家是汽车的速度是每小时15千米.
故答案为:30,15,1,15.
【点评】此题考查从统计图表中获取信息,仔细观察领悟图意,获取信息,用这些信息解决实际问题即可.
11.【分析】1)根据统计图可知:汽车出发时的时间是7:55,行驶到15千米时的时间是8:20,用路程除以时间等于速度解答即可.
(2)用火车开出的时间减去到站的时间就是火车停站的时间
(3)先求出火车停站后的时速,再减去汽车的时速即可,
(4)用火车到站的时间减去汽车到站的时间就是汽车比火车早到的时间,
【解答】解:(1)8:20﹣7:55=25(分钟),
15÷25=(千米/分钟)
(2)8时10分﹣8时=10分钟
(3)8时25分﹣8时10分=15(分钟)
15﹣5=10(千米)
10÷15﹣=(千米/分钟)
(4)8时25分﹣8时20分=5(分钟)
故答案为:千米/分钟,10分钟,千米/分钟,5分钟.
【点评】本题主要考查了学生根据统计图,分析数量关系解答问题的能力.
12.【分析】观察统计图可知,甲飞机飞了40秒,乙飞机飞了35秒,甲飞机飞行的时间长一些,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大,第15秒至第20秒乙飞机的飞行水平行驶状态.
【解答】解:(1)这两架飞机中,甲飞机的飞行时间长一些.
(2)起飞后第15秒两架飞机处于同一高度.起飞后第30秒两架飞机的高度相差最大.
(3)从起飞后两架飞机第15秒至第20秒乙飞机的飞行情况水平直线行驶状态.
故答案为:甲,15,30,水平直线行驶状态.
【点评】本题主要考查了从折线统计图中读出数据的能力,注意两架模型飞机不是同时落地的.
13.【分析】(1)根据线段图,从学校去动物园的途中,11:00到达动物园,学生游玩动物园的时间是16﹣11=5(小时),即停车时间;
(2)停车前的一段路上,汽车行驶的时间是11﹣8=3(小时),路程为80千米,则速度为80÷(11﹣8)千米/时;
(3)根据线段图,汽车在动物园停车5小时后,16:00再次出发,18:00时到达,因此经过2时到达动物园,平均速度是80÷2=40(千米),解决此题;
(4)根据线段图,可看出16:00﹣18:00这个时间段线段最陡直,因此16:00﹣18:00这个时间汽车行驶得最快;若去和回都按这样的速度匀速行驶(中途不停车),学生游玩动物园的时间为16﹣11=5(小时),共用时间为80×2÷40+(16﹣11)]=9(时),节省时间为10﹣9,解决问题.
【解答】解:(1)16﹣11=5(小时);
答:从学校去动物园的途中,停车5时.
(2)80÷(11﹣8),
=80÷3,
=(小时);
答:停车前的一段路上平均每时行驶千米.
(3)18﹣16=2(时),
80÷2=40(千米);
答:停车后再次出发,又经过2时到达动物园.行驶这一段路,平均每时行驶40千米.
(4)在汽车的行驶过程中,18:00﹣16:00这个时间段汽车行驶得最快.
节省时间:
(18﹣8)﹣[80×2÷40+(16﹣11)],
=10﹣[4+(16﹣11)],
=10﹣9,
=1(时);
答:在汽车的行驶过程中,18:00﹣16:00这个时间段汽车行驶得最快.共可节省时间1时0分.
【点评】此题考查学生对折线统计图的分析以及对行程问题的掌握情况.
14.【分析】通过观察折线统计图,可以看出从家出发经过60分钟=1小时到达图书馆,在图书馆活动用了40分钟=小时,然后用了40分钟=小时返回到家.由此即可解决问题.
【解答】解:从折线统计图可以看出:在图书馆借书用40分=小时;
去时平均速度是:6000÷60=100(米);
返回时的平均速度是:6000÷40=150(米);
故答案为:,100,150.
【点评】此题考查了利用折线统计图表示行走时间和行走路程的关系,以及通过观察统计图得出行走时间与路程来解决问题的方法.
15.【分析】(1)根据统计图可知:甲游了
60米追上乙;
(2)由图可知:甲行了(55﹣10)秒,行了120米,求甲的速度,根据:路程÷时间=速度,由此解答即可.
【解答】解:(1)根据统计图可知:甲游了
60米追上乙;
(2)120÷(55﹣10)
=120÷45
=(米)
答:甲的速度是米/秒.
故答案为:60,.
【点评】此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法.
16.【分析】(1)根据此图判断是路程﹣时间图,找准一个点,用路程除以对应的走此路程所用的时间就是速度,如甲车8:00至9:40对应的路程90千米,用90除以1小时,即可得解;
(2)乙车8:00至10:00对应的路程是90千米,用90除以2小时求出乙的速度,然后根据题意进行比,即可求出甲、乙两车的速度比;
(3)分别求出出甲车小时行的路程与乙车小时行的路程,最后用甲车行的路程减去乙车行的路程即可.
【解答】解:(1)9时40分=9时
甲车每小时行驶:
90÷(9﹣8)
=90÷1
=90×
=54(千米)
答:甲车每小时行驶54千米.
(2)乙车每小时行驶:
90÷(10﹣8)
=90÷2
=45(千米)
54:45
=(54÷9):(45÷9)
=6:5
答:甲、乙两车速度的最简整数比是6:5.
(3)54×﹣45×
=36﹣30
=6(千米)
答:同向而行时后,两车相距6千米.
故答案为:54,6,5,6.
【点评】解答此图的关键是:会看懂此图,根据速度,路程,时间的关系,找出数量关系,列式解答即可.
三.操作题(共2小题)
17.【分析】根据所给数据绘制复式折线统计图即可.
【解答】解:如图所示:
【点评】本题主要考查复式折线统计图的绘制,关键分清实际产量和计划产量.
18.【分析】(1)由统计图观察可知,他们在9:00到达A风景区,10:00离开,所以他在风景区玩了10:00﹣9:00=1小时,11:00到达B风景区,14:00离开,所以他在风景区玩了14:00﹣11:00=3小时;
(2)由统计图观察可知,他们到达B景区的路程是140千米;
(3)根据观察可知他们14:00开始返回即是下午2:00,16:00到家,即是下午4:00.
【解答】解:(1)他们9:00时到达A景区,停留了1小时.11:00时到达B景区,停留了3小时.
(2)B景区离圆圆家的路程是140km.
(3)他们下午2:00时开始返回,下午4:00时到家.
故答案为:9:00,1,11:00,3,140,2:00,4:00.
【点评】本题主要考查了学生根据折线统计图分析数量关系解答问题的能力.
四.应用题(共10小题)
19.【分析】(1)通过观察统计图,可知A型号的电动汽车销量大些;
(2)如果你是经销部经理,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【解答】解:(1)A型号的电动汽车销量大些;
(2)上图反映,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【点评】此题考查根据统计表提供的信息,解决实际问题的能力.
20.【分析】(1)根据复式折线统计图可知:表示两款车销量的折线距离最大的6月,两款车的销量差距最大.
(2)根据折线统计图中的数据,把B款车六个月的销量求和,然后求平均数即可.
【解答】解:(1)答:6月份两款新车的销售量差距最大.
(2)210+158+260+390+370+340=1728(辆)
1728÷6=288(辆)
答:B款车在6个月内一共销售1728辆;平均每个月销售288辆.
【点评】本题主要考查复式折线统计图,关键根据统计图中所给数据做题.
21.【分析】(1)根据一天浪费的水,求一个月浪费的水:80×30=2400(千克),2400千克=2.4吨,根浪费水量和时间的正比例关系绘制折线统计图即可.
(2)根据一户一个月浪费的水量,求100户一年浪费的水量即可.
【解答】解:80×30=2400(千克)
2400千克=2.4吨
如图所示:
(2)2.4×12×100=2880(吨)
答:100户家庭一年要浪费2880吨.
【点评】本题主要考察折线统计图的绘制,关键根据浪费水量和时间的关系作图.
22.【分析】(1)通过长折线统计图可知,小军在途中一共休息了2次,第一次休息15分钟,第二次休息了15分钟,根据加法的意义,把两次休息的时间合并起来即可.
(2)通过观察统计图可知,小军7:30从家出发,11:00回到家,用回到家的时刻减去出发的时刻就是一共用的时间,据此列式解答.
【解答】解:(1)15+15=30(分钟)
答:小军在途中一共休息了2次,共30分钟.
(2)11时﹣7时30分=3时30分
3时30分=3.5小时
答:小军从家出发到返回家一共用了3.5小时.
故答案为:2,30;3.5.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.【分析】(1)两个车间2012年的750万元,到2015年,三车间达到2000万元,而四车间只有1500万元,显然四车间增长较快.
(2)2012年相差0万元;2013年相差1250﹣1000=250(万元);2014年相差1500﹣1100=400(万元);2015年相差2000﹣1500=500(万元).由此看出2015年两车间的工业产值相差最大.
(3)就是求2015年比2014年增长的产值占2014年产值的几分之几,用2015年比2014年增长的产值除以2014年的产值.
【解答】解:(1)三车间的工业产值增长较快.
(2)2015年两车间的工业产值相差最大.
(3)(1500﹣1100)÷1100
=400÷1100
=
答:四车间2015年的工业产值比2014年增长.
故答案为:三,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
24.【分析】(1)由复式折线统计图可以看出,2011年未分类的垃圾为12.5万吨,分类的是8万吨,垃圾总量为12.5+8=20.5(万吨),用分类垃圾的吨数除以总吨数;同理,2015年未分类的垃圾为16万吨,分类的是1万吨,垃圾总量为16+11=27(万吨),用分类垃圾的吨数除以总吨数.
(2)由复式折线统计图可以看出,表示未分类垃圾、分类垃圾的点,2010年距离最大,说明该年两种垃圾相差最多;表示分类垃圾的折线从2015年在表示未分类垃圾折线的上方,说明该年开始分类垃圾超过了未分类垃圾.
(3)垃圾分类处理的好处有:减少占地;减少污染;变废为宝;减少危害.看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
【解答】解:(1)8÷(12.5+8)
=8÷20.5
=
11÷(16+11)
=11÷27
=
答:2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的.
(2)答:两种垃圾相差最多的是
2010年,从
2015年开始分类垃圾超过了未分类垃圾.
(3)答:的感想和建议:看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
故答案为:2010,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
25.【分析】(1)1、2、3月份各月凉鞋的销售双数已知,三者相加就是第一季度共销售凉鞋的双数.
(2)用7月份销售凉鞋的双数除以5月份销售凉鞋的双数.
(3)由统计图即可看出,7月份凉鞋的销售量最高.原因:我国处于北半球北温带,7月份气温最高.
(4)8月份开始气温开始下降,凉鞋的销售量也会明显减少,要少于6月份的销售量,9、10月份更低,111月份开始估计停止销售.据此即可完成这幅统计图(答案不唯一).
【解答】解:(1)20+30+50=100(双)
答:第一季度共销售100双.
(2)500÷200=5
答:7月份的销售量是5月份的5倍.
(3)图中7月份凉鞋的销售量最高.原因:7月份气温最高.
(4)完成这幅折线统计图:
故答案为:100,5,7.
【点评】此题是考查如何从单式折线统计图中获取信息,并根据所获取的信息解决实际问题.
26.【分析】通过观察折线统计图可知:单开A管15分钟水位上升到20分米,两管同时开5分钟水位上升了(40﹣20)分米,根据“等分”除法的意义,用除法解答即可.
【解答】解:(40﹣20)÷(20﹣15)
=20÷5
=4(分米),
答:每分钟水位上升4分米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
27.【分析】通过观察折线统计图可知:甲车2小时行驶150千米,因为=速度(一定),所以路程和时间成正比例,设3.5小时行驶x千米,据此列比例解答.
【解答】解:设3.5小时行驶x千米,
=
2x=3.5×150
x=
x=262.5.
答:3.5小时行驶262.5千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
28.【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据完成统计图.
(2)两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
【解答】解:(1)作图如下:
(2)18﹣5=13(℃);
答:两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
故答案为:2、13℃.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题.
折线统计图》单元测试题
一.选择题(共8小题)
1.星期天晚饭后,小红从家里出去散步,如图描述了她散步过程中离家的距离s(m)与散步所用时间t(分)之间的关系.依据统计图,下面描述符合小红散步情景的是( )
A.从家里出发,到一个公共阅报亭看了一会儿报,就回家了
B.从家出发,到了一个公共阅报亭看了一会儿报后,继续向前走了一段,然后回家了
C.从家出发,一直散步(没有停留),然后回来了
D.从家出发,散了一会儿步,就找同学去了,l8分钟后才开始返回
2.华侨商场有四层楼.小红开始在三楼买了点心,再到二楼买了学习用品,又上到四楼买衣服,最后回到一楼买了玩具.比较准确地描述这件事是( )
A.
B.
C.
D.
3.早晨张爷爷步行20分到离家1500米的广场锻炼身体,1时后,张爷爷步行20分回家吃饭,( )反映了张爷爷这一活动行程.
A.
B.
C.
D.
4.如下图,反映室内温度变化情况正确的折线统计图是( )
A.
B.
C.
5.一脚踢出去的足球,反映它的高度与时间的关系是图中( )
A.
B.
C.
D.
6.对复式折线统计图的优点描述最准确的是( )
A.能看出数量的多少
B.可以看出数量的增减变化
C.折线较多,很美观
D.不仅能看出数量的多少和增减变化的情况,而且方便对两组相关数据进行比较
7.一只兔子和一条小狗从同一地点出发,同时开始向东运动,兔子的运动距离与时间关系图象如图中实线部分ABCD所示,小狗的运动距离与时间关系图象如图中虚线部分AD所示.则关于该图象下列说法正确的是( )
A.小狗的速度始终比兔子快
B.整个过程中小狗和兔子的平均速度相同
C.图中BC段表明兔子在做匀速直线运动
D.在前4秒内,小狗比兔子跑得快
8.小强跑步的速度是( )
A.先快后慢
B.先慢后快
C.匀速
D.无法确定
二.填空题(共8小题)
9.一次越野赛跑中,当小明跑了1600米时,小刚跑了1300米.小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的关系如图,则这次越野跑的全程为
米.
10.如图,描述的是一位自行车爱好者从家出发去某地及他回到家中,行驶的距离与所用时间的关系,骑车者9时从家出发,15时回到家中,根据这个折线图填空.
(1)骑车者最远时离家是
千米
(2)11时到12时他骑了
千米
(3)他此次出发至最远处时休息了
小时
(4)他回家时骑车的速度是每小时
千米.
11.下面是一辆汽车与一列火车行程图表,根据图解答:
(1)汽车时速是多少千米?列式计算
(2)火车停站时间是多少分钟?列式计算
(3)火车停站后时速比汽车快多少千米?列式计算
(4)汽车比火车早到多少分钟?列式计算
.
12.下面是航模兴趣小组制作的两架模型飞机在一次飞行中飞行时间和高度的记录.
(1)这两架飞机中,
飞机的飞行时间长一些.
(2)起飞后第
秒两架飞机处于同一高度.起飞后第
秒两架飞机的高度相差最大.
(3)说说从起飞后两架飞机第15秒至第20秒乙飞机的飞行情况.
.
13.六(1)班同学乘车去动物园,然后返回学校..他们的行程情况如图.
(1)从学校去动物园的途中,停车
时.
(2)停车前的一段路上平均每时行驶
千米.
(3)停车后再次出发,又经过
时到达动物园.行驶这一段路,平均每时行驶
千米.
(4)在汽车的行驶过程中,
这个时间段汽车行驶得最快.若去和回都按这样的速度匀速行驶(中途不停车),学生游玩动物园的时间不变,那么共可节省时间
时
分.
14.小芳骑自行车从学校去相距6千米的图书馆,看折线统计图求出小芳在图书馆活动用了
小时,去时平均速度是每分钟行
米,返回速度每分钟行
米.
15.甲、乙两名游泳运动员进行200米游泳比赛,甲让乙先游10秒.赛后,制作了如下的图象.
(1)甲游了
米追上乙.
(2)甲的速度是
米/秒.
16.根据甲、乙两车的行程图填空.
(1)甲车每小时行驶
千米.
(2)甲、乙两车速度的最简整数比是
:
.
(3)甲、乙两车8:00从同一地点出发,同向而行时后,两车相距
千米.
三.操作题(共2小题)
17.某水泥厂第一季度生产情况如下:
1月份计划生产水泥400吨,实际生产450吨;2月份计划生产400吨,实际生产440吨;3月份计划生产水泥500吨,实际生产600吨.
请完成折线统计图.
18.星期天,圆圆随父母去旅游,先游览了A景区,后又游览了B景区.如图是出发后各时刻圆圆离家路程统计图.
(1)他们
时到达A景区,停留了
小时.
时到达B景区,停留了
小时.
(2)B景区离圆圆家的路程是
km.
(3)他们下午
时开始返回,下午
时到家.
四.应用题(共10小题)
19.某电动汽车经销部某一周销售情况如图:
(1)哪种型号的电动汽车销量大些?
(2)如果你是经销部经理,上图反映的信息对你有什么帮助?
20.如图是某汽车厂两款新车销售情况统计图.
根据图中数据,回答下面的问题.
(1)几月份两款新车的销售量差距最大?
(2)B款车在6个月内一共销售多少辆?平均每个月销售多少辆?
21.一个漏水的水龙头一天要浪费80kg水.(一个月按30天计算)
(1)请你根据计算完成下面的折线统计图.
(2)若100户家庭各有1个水龙头按这样的速度漏水,则这100户家庭一年要浪费多少吨水?
22.小军到离家6km远的奶奶家看望奶奶,请根据折线统计图回答问题.
(1)小军途中一共休息了
次,共
分钟.
(2)小军从家出发到返回家一共用了
小时.
23.如图是某纺织厂2012﹣2015年三、四车间工业产值增长情况统计图.
(1)
车间的工业产值增长较快.
(2)
年两车间的工业产值相差最大.
(3)四车间2015年的工业产值比2014年增长几分之几?
24.某城市2010﹣2015年生活垃圾中分类垃圾与未分类垃圾质量如图:
(1)2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的
(2)两种垃圾相差最多的是
年,从
年开始分类垃圾超过了未分类垃圾.
(3)看了这幅图后你有什么感想或建议.
25.某商场2018年凉鞋的销售情况如图所示.
(1)第一季度共销售
双.
(2)7月份的销售量是5月份的
倍.
(3)图中
月份凉鞋的销售量最高,原因是什么?
(4)这是一幅不完整的折线统计图.请你根据生活实际,完成这幅折线统计图.
26.水池有A、B两个进水管,先开A管,过一段时间后两管同时打开.当A、B管同时打开后,每分钟水位上升多少分米?
27.如图是甲车行驶的路程与时间的关系图.甲车3.5时行驶多少千米?
28.下表是某年云南省玉溪市和四川省成都市月平均气温统计表.(单位:C)(1分;
月份
1
2
3
4
5
6
7
8
9
10
11
12
玉溪市
16
18
21
25
27.5
28
27
26.5
26
25
22
17
成都市
4
5
10
16
21
26
29
29
23.5
17.5
11
5.5
(1)根据上表中的数据,绘制复式折线统计图.
(2)两个城市气温相差最大的是
月,相差
.
(3)简单描述两个城市全年气温变化情况.
(4)哪个城市全年气温相对稳定一些?
参考答案与试题解析
一.选择题(共8小题)
1.【分析】根据图象可知,有一段时间内时间在增加,而路程没有增加,意味着有停留,与x轴平行后的函数图象表现为随时间的增多路程又在增加,由此即可作出判断.
【解答】解:从图中看,有一段时间内函数图象与x轴平行,说明时间在增加,而路程没有增加,C、D中没有停留,所以排除C、D.与x轴平行后的函数图象表现为随时间的增多路程又在增加,排除A.
故选:B.
【点评】读懂图象是解决本题的关键.首先应理解函数图象的横轴和纵轴表示的量,再根据函数图象用排除法判断.
2.【分析】根据题意和统计图,因为小红去的楼层各不相同,A显然不正确;B表示先去了4层,因此也不正确;C表示先去三楼,再去二楼,然后去四楼,最后去了一楼,故正确;D表示先去了一楼,因此也不正确.据此解答.
【解答】解:A显然不正确;
B表示先去了4层,因此也不正确;
C表示先去三楼,再去二楼,然后去四楼,最后去了一楼,故正确;
D表示先去了一楼,因此也不正确.
故选:C.
【点评】此题先理解题意,再分析统计图,考查了学生分析统计图的能力.
3.【分析】根据题意可知,张爷爷步行从0分钟到20分钟处于行驶状态折线统计图中的折线应是上升状态,20分钟后到达广场锻炼身体,直到20+60=80分钟有开始步行回家,所以在20分钟到80分钟之间折线处于持平状态,在80分钟到100分钟之间张爷爷开始返回家中,所以折线图应是下降状态,根据分析进行选择即可得到答案.
【解答】解:A、由图可知,在20分钟到80分钟之间折线处于持平状态;
B、由图可知,在20分钟到40分钟折线处于持平状态,在40分钟后到60分钟折线又处于持平状态;
C、折线直接从20分钟开始直线上升,没有匀速行驶的过程;
D、折线从40分钟到80分钟之间处于持平状态,锻炼时间为80﹣40=40分钟.
所以选项A反映了张爷爷这一活动行程.
故选:A.
【点评】解决关键是观察统计图,弄清楚横轴和纵轴分别表示什么量,进而根据折线情况解答问题
4.【分析】根据以上折线统计图的数据,一天中13时的气温达到一天中的最高值,由此判断折线统计图C正确.
【解答】解:一天中13时的气温达到一天中的最高值,
所以反映室内温度变化情况正确的折线统计图是C.
故选:C.
【点评】此题主要考查折线统计图的特点,并能根据它的特点解决有关的实际问题.
5.【分析】根据提出的足球应该是首先上升再下降过程,得出符合要求图象即可.
【解答】解:根据一脚踢出去的球的高度与时间的关系,应该是首先上升再下降过程,所以只有A符合要求.
故选:A.
【点评】解答此题的关键是弄清足球开始和最后与地面的距离为0.
6.【分析】根据三种统计图的优点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此解答即可.
【解答】解:答:对复式折线统计图的优点描述最准确的是不仅能看出数量的多少和增减变化的情况,而且方便对两组相关数据进行比较.
故选:D.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用.
7.【分析】由图象可以看出:在前4秒,兔子在相同时间内通过的路程比小狗的路程多,所以兔子的运动速度大于小狗的运动速度(由此判断选项D错误);在第4秒,小狗和兔子在相同时间内通过相同的路程,所以它们的平均速度相同;在4到8秒的时间段,小狗在相同时间内通过的路程比兔子的路程多,所以小狗的运动速度大于兔子的运动速度.整个过程中,小狗和兔子运动路程相同,运动时间相同,所以它们的平均速度相同,选项A是错误的,B正确.另,图中的BC段表示兔子处于静止状态.
【解答】解:由分析得:在前4秒,兔子在相同时间内通过的路程比小狗的路程多,所以兔子的运动速度大于小狗的运动速度.由此判断选项A和D错误;
在第4秒,图中的BC段表示兔子处于静止状态,由此判断选项C是错误的;
在4到8秒的时间段,小狗在相同时间内通过的路程比兔子的路程多,所以小狗的运动速度大于兔子的运动速度.整个过程中,小狗和兔子运动路程相同,运动时间相同,所以它们的平均速度相同,选项B正确.
故选:B.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息作出判断和预测.
8.【分析】由表示小强、小刚跑步的折线可以看出:小刚先比小强跑得快,到3分半时,被小强追上反超,从此比小强跑得慢,即先快后慢,最终跑完用时比小强多;小强先比小刚慢,到3分半时追上小刚,并且一直领先,表示小强跑得速度的折线几乎是直线,说明小强几乎是匀速跑的.
【解答】解:如图
小强跑步的速度是匀速.
故选:C.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
二.填空题(共8小题)
9.【分析】设小明的速度为a米/秒,小刚的速度为b米/秒,根据统计图,由行程问题的数量关系建立方程组:,求出其解,进而解决问题.
【解答】解:设小明的速度为a米/秒,小刚的速度为b米/秒,由题意,得:
,
②﹣①得:b=2a,
把b=2a代入①得:a=3,
则b=2×3=6,
所以,
所以这次越野跑的全程为:
1600+300×3
=1600+900
=2500(米).
答:这次越野跑的全程为2500米.
故答案为:2500.
【点评】本题考查了行程问题的数量关系的运用,由统计图的数量关系建立方程组是解答的关键.
10.【分析】(1)由统计图可知:观骑车者最远时离家是30千米;
(2)11时到12时他骑了30﹣15=15千米;
察函数图象得到E点表示离家最远,然后读出E点坐标可得到离家最远的时间与离家的距离;
(3)他此次出发至最远处时休息了13时﹣12时=1小时;
(4)根据速度=路程÷时间进行解答即可.
【解答】解:(1)由统计图可知:观骑车者最远时离家是30千米;
(2)30﹣15=15(千米);
答:11时到12时他骑了15千米.
(3)13时﹣12时=1小时;
答:他此次出发至最远处时休息了1小时.
(4)30÷(15﹣13)
=30÷2
=15(千米);
答:他回家是汽车的速度是每小时15千米.
故答案为:30,15,1,15.
【点评】此题考查从统计图表中获取信息,仔细观察领悟图意,获取信息,用这些信息解决实际问题即可.
11.【分析】1)根据统计图可知:汽车出发时的时间是7:55,行驶到15千米时的时间是8:20,用路程除以时间等于速度解答即可.
(2)用火车开出的时间减去到站的时间就是火车停站的时间
(3)先求出火车停站后的时速,再减去汽车的时速即可,
(4)用火车到站的时间减去汽车到站的时间就是汽车比火车早到的时间,
【解答】解:(1)8:20﹣7:55=25(分钟),
15÷25=(千米/分钟)
(2)8时10分﹣8时=10分钟
(3)8时25分﹣8时10分=15(分钟)
15﹣5=10(千米)
10÷15﹣=(千米/分钟)
(4)8时25分﹣8时20分=5(分钟)
故答案为:千米/分钟,10分钟,千米/分钟,5分钟.
【点评】本题主要考查了学生根据统计图,分析数量关系解答问题的能力.
12.【分析】观察统计图可知,甲飞机飞了40秒,乙飞机飞了35秒,甲飞机飞行的时间长一些,起飞后第15秒两架飞机处于同一高度,起飞后大约30秒两架飞机的高度相差最大,第15秒至第20秒乙飞机的飞行水平行驶状态.
【解答】解:(1)这两架飞机中,甲飞机的飞行时间长一些.
(2)起飞后第15秒两架飞机处于同一高度.起飞后第30秒两架飞机的高度相差最大.
(3)从起飞后两架飞机第15秒至第20秒乙飞机的飞行情况水平直线行驶状态.
故答案为:甲,15,30,水平直线行驶状态.
【点评】本题主要考查了从折线统计图中读出数据的能力,注意两架模型飞机不是同时落地的.
13.【分析】(1)根据线段图,从学校去动物园的途中,11:00到达动物园,学生游玩动物园的时间是16﹣11=5(小时),即停车时间;
(2)停车前的一段路上,汽车行驶的时间是11﹣8=3(小时),路程为80千米,则速度为80÷(11﹣8)千米/时;
(3)根据线段图,汽车在动物园停车5小时后,16:00再次出发,18:00时到达,因此经过2时到达动物园,平均速度是80÷2=40(千米),解决此题;
(4)根据线段图,可看出16:00﹣18:00这个时间段线段最陡直,因此16:00﹣18:00这个时间汽车行驶得最快;若去和回都按这样的速度匀速行驶(中途不停车),学生游玩动物园的时间为16﹣11=5(小时),共用时间为80×2÷40+(16﹣11)]=9(时),节省时间为10﹣9,解决问题.
【解答】解:(1)16﹣11=5(小时);
答:从学校去动物园的途中,停车5时.
(2)80÷(11﹣8),
=80÷3,
=(小时);
答:停车前的一段路上平均每时行驶千米.
(3)18﹣16=2(时),
80÷2=40(千米);
答:停车后再次出发,又经过2时到达动物园.行驶这一段路,平均每时行驶40千米.
(4)在汽车的行驶过程中,18:00﹣16:00这个时间段汽车行驶得最快.
节省时间:
(18﹣8)﹣[80×2÷40+(16﹣11)],
=10﹣[4+(16﹣11)],
=10﹣9,
=1(时);
答:在汽车的行驶过程中,18:00﹣16:00这个时间段汽车行驶得最快.共可节省时间1时0分.
【点评】此题考查学生对折线统计图的分析以及对行程问题的掌握情况.
14.【分析】通过观察折线统计图,可以看出从家出发经过60分钟=1小时到达图书馆,在图书馆活动用了40分钟=小时,然后用了40分钟=小时返回到家.由此即可解决问题.
【解答】解:从折线统计图可以看出:在图书馆借书用40分=小时;
去时平均速度是:6000÷60=100(米);
返回时的平均速度是:6000÷40=150(米);
故答案为:,100,150.
【点评】此题考查了利用折线统计图表示行走时间和行走路程的关系,以及通过观察统计图得出行走时间与路程来解决问题的方法.
15.【分析】(1)根据统计图可知:甲游了
60米追上乙;
(2)由图可知:甲行了(55﹣10)秒,行了120米,求甲的速度,根据:路程÷时间=速度,由此解答即可.
【解答】解:(1)根据统计图可知:甲游了
60米追上乙;
(2)120÷(55﹣10)
=120÷45
=(米)
答:甲的速度是米/秒.
故答案为:60,.
【点评】此题考查了利用折线统计图表达行驶路程与时间关系及利用统计图中数据解决实际问题的方法.
16.【分析】(1)根据此图判断是路程﹣时间图,找准一个点,用路程除以对应的走此路程所用的时间就是速度,如甲车8:00至9:40对应的路程90千米,用90除以1小时,即可得解;
(2)乙车8:00至10:00对应的路程是90千米,用90除以2小时求出乙的速度,然后根据题意进行比,即可求出甲、乙两车的速度比;
(3)分别求出出甲车小时行的路程与乙车小时行的路程,最后用甲车行的路程减去乙车行的路程即可.
【解答】解:(1)9时40分=9时
甲车每小时行驶:
90÷(9﹣8)
=90÷1
=90×
=54(千米)
答:甲车每小时行驶54千米.
(2)乙车每小时行驶:
90÷(10﹣8)
=90÷2
=45(千米)
54:45
=(54÷9):(45÷9)
=6:5
答:甲、乙两车速度的最简整数比是6:5.
(3)54×﹣45×
=36﹣30
=6(千米)
答:同向而行时后,两车相距6千米.
故答案为:54,6,5,6.
【点评】解答此图的关键是:会看懂此图,根据速度,路程,时间的关系,找出数量关系,列式解答即可.
三.操作题(共2小题)
17.【分析】根据所给数据绘制复式折线统计图即可.
【解答】解:如图所示:
【点评】本题主要考查复式折线统计图的绘制,关键分清实际产量和计划产量.
18.【分析】(1)由统计图观察可知,他们在9:00到达A风景区,10:00离开,所以他在风景区玩了10:00﹣9:00=1小时,11:00到达B风景区,14:00离开,所以他在风景区玩了14:00﹣11:00=3小时;
(2)由统计图观察可知,他们到达B景区的路程是140千米;
(3)根据观察可知他们14:00开始返回即是下午2:00,16:00到家,即是下午4:00.
【解答】解:(1)他们9:00时到达A景区,停留了1小时.11:00时到达B景区,停留了3小时.
(2)B景区离圆圆家的路程是140km.
(3)他们下午2:00时开始返回,下午4:00时到家.
故答案为:9:00,1,11:00,3,140,2:00,4:00.
【点评】本题主要考查了学生根据折线统计图分析数量关系解答问题的能力.
四.应用题(共10小题)
19.【分析】(1)通过观察统计图,可知A型号的电动汽车销量大些;
(2)如果你是经销部经理,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【解答】解:(1)A型号的电动汽车销量大些;
(2)上图反映,应多进A型号的电动汽车,因为A型号的电动汽车销售量大些.
【点评】此题考查根据统计表提供的信息,解决实际问题的能力.
20.【分析】(1)根据复式折线统计图可知:表示两款车销量的折线距离最大的6月,两款车的销量差距最大.
(2)根据折线统计图中的数据,把B款车六个月的销量求和,然后求平均数即可.
【解答】解:(1)答:6月份两款新车的销售量差距最大.
(2)210+158+260+390+370+340=1728(辆)
1728÷6=288(辆)
答:B款车在6个月内一共销售1728辆;平均每个月销售288辆.
【点评】本题主要考查复式折线统计图,关键根据统计图中所给数据做题.
21.【分析】(1)根据一天浪费的水,求一个月浪费的水:80×30=2400(千克),2400千克=2.4吨,根浪费水量和时间的正比例关系绘制折线统计图即可.
(2)根据一户一个月浪费的水量,求100户一年浪费的水量即可.
【解答】解:80×30=2400(千克)
2400千克=2.4吨
如图所示:
(2)2.4×12×100=2880(吨)
答:100户家庭一年要浪费2880吨.
【点评】本题主要考察折线统计图的绘制,关键根据浪费水量和时间的关系作图.
22.【分析】(1)通过长折线统计图可知,小军在途中一共休息了2次,第一次休息15分钟,第二次休息了15分钟,根据加法的意义,把两次休息的时间合并起来即可.
(2)通过观察统计图可知,小军7:30从家出发,11:00回到家,用回到家的时刻减去出发的时刻就是一共用的时间,据此列式解答.
【解答】解:(1)15+15=30(分钟)
答:小军在途中一共休息了2次,共30分钟.
(2)11时﹣7时30分=3时30分
3时30分=3.5小时
答:小军从家出发到返回家一共用了3.5小时.
故答案为:2,30;3.5.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
23.【分析】(1)两个车间2012年的750万元,到2015年,三车间达到2000万元,而四车间只有1500万元,显然四车间增长较快.
(2)2012年相差0万元;2013年相差1250﹣1000=250(万元);2014年相差1500﹣1100=400(万元);2015年相差2000﹣1500=500(万元).由此看出2015年两车间的工业产值相差最大.
(3)就是求2015年比2014年增长的产值占2014年产值的几分之几,用2015年比2014年增长的产值除以2014年的产值.
【解答】解:(1)三车间的工业产值增长较快.
(2)2015年两车间的工业产值相差最大.
(3)(1500﹣1100)÷1100
=400÷1100
=
答:四车间2015年的工业产值比2014年增长.
故答案为:三,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
24.【分析】(1)由复式折线统计图可以看出,2011年未分类的垃圾为12.5万吨,分类的是8万吨,垃圾总量为12.5+8=20.5(万吨),用分类垃圾的吨数除以总吨数;同理,2015年未分类的垃圾为16万吨,分类的是1万吨,垃圾总量为16+11=27(万吨),用分类垃圾的吨数除以总吨数.
(2)由复式折线统计图可以看出,表示未分类垃圾、分类垃圾的点,2010年距离最大,说明该年两种垃圾相差最多;表示分类垃圾的折线从2015年在表示未分类垃圾折线的上方,说明该年开始分类垃圾超过了未分类垃圾.
(3)垃圾分类处理的好处有:减少占地;减少污染;变废为宝;减少危害.看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
【解答】解:(1)8÷(12.5+8)
=8÷20.5
=
11÷(16+11)
=11÷27
=
答:2011年分垃圾占垃圾总量的,2015年分类垃圾占垃圾总量的.
(2)答:两种垃圾相差最多的是
2010年,从
2015年开始分类垃圾超过了未分类垃圾.
(3)答:的感想和建议:看了这幅图感到人们的环保意识在增强,感到欣慰;建议所有垃圾能够完全分类.
故答案为:2010,2015.
【点评】此题是考查如何从复式折线统计图中获取信息,并根据所获取的信息解决实际问题.
25.【分析】(1)1、2、3月份各月凉鞋的销售双数已知,三者相加就是第一季度共销售凉鞋的双数.
(2)用7月份销售凉鞋的双数除以5月份销售凉鞋的双数.
(3)由统计图即可看出,7月份凉鞋的销售量最高.原因:我国处于北半球北温带,7月份气温最高.
(4)8月份开始气温开始下降,凉鞋的销售量也会明显减少,要少于6月份的销售量,9、10月份更低,111月份开始估计停止销售.据此即可完成这幅统计图(答案不唯一).
【解答】解:(1)20+30+50=100(双)
答:第一季度共销售100双.
(2)500÷200=5
答:7月份的销售量是5月份的5倍.
(3)图中7月份凉鞋的销售量最高.原因:7月份气温最高.
(4)完成这幅折线统计图:
故答案为:100,5,7.
【点评】此题是考查如何从单式折线统计图中获取信息,并根据所获取的信息解决实际问题.
26.【分析】通过观察折线统计图可知:单开A管15分钟水位上升到20分米,两管同时开5分钟水位上升了(40﹣20)分米,根据“等分”除法的意义,用除法解答即可.
【解答】解:(40﹣20)÷(20﹣15)
=20÷5
=4(分米),
答:每分钟水位上升4分米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
27.【分析】通过观察折线统计图可知:甲车2小时行驶150千米,因为=速度(一定),所以路程和时间成正比例,设3.5小时行驶x千米,据此列比例解答.
【解答】解:设3.5小时行驶x千米,
=
2x=3.5×150
x=
x=262.5.
答:3.5小时行驶262.5千米.
【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.
28.【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据完成统计图.
(2)两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
【解答】解:(1)作图如下:
(2)18﹣5=13(℃);
答:两个城市气温相差最大的是2月份,相差13℃.
(3)通过观察折线统计图可知:玉溪市月平均气温从1月到6月呈上升趋势,从7月到12月呈下降趋势;成都市月平均气温从1月到到8月呈上升趋势,从9月到12月呈下降趋势.
(4)通过比较发现,玉溪市全年气温相对稳定一些.
故答案为:2、13℃.
【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图提供的信息,解决有关的实际问题.
