六年级下册数学课件 第三单元《第2课时 圆锥的体积(1)》人教版 (共28张PPT)
文档属性
| 名称 | 六年级下册数学课件 第三单元《第2课时 圆锥的体积(1)》人教版 (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 20:50:52 | ||
图片预览







文档简介
(共28张PPT)
第三单元
第2课时
圆锥的体积(1)
人教版数学六年级下册
学习目标
1.理解圆锥体积公式的推导过程,初步掌握圆锥体积的计算公式,并能运用公式正确地计算圆锥的体积。
2.进行比较、分析、综合、猜测,在感知的基础上加以判断、推理来获取新知识。
同学们,今天我们一起来学习圆锥体积的计算方法。
导入新知
1.开展实验,收集数据。
圆锥的体积究竟和圆柱的体积有什么关系?
这里有沙子和水,还有等底等高和不等底和不等高的各种圆柱、圆锥的模型。
合作探究
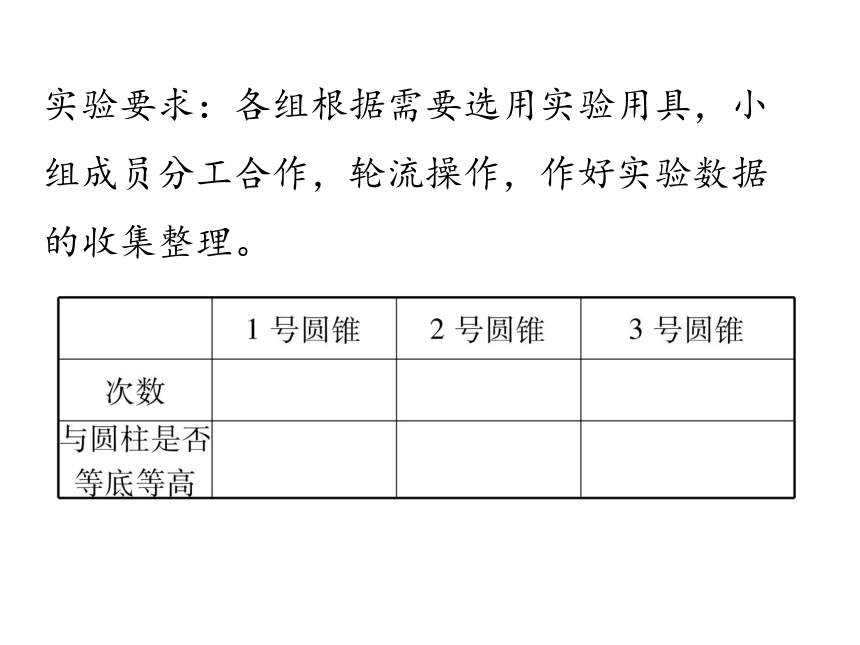
实验要求:各组根据需要选用实验用具,小组成员分工合作,轮流操作,作好实验数据的收集整理。
2.分析数据,做出判断。
观察全班实验数据,你发现了什么?
发现大多数情况下圆柱能装下三个圆锥的沙或水,也有两个多或四个等不同结果。
进一步观察分析,什么情况下圆柱刚好能装下三个圆锥的沙或水?
各组互相观察各自的圆柱、圆锥,发现只要是等底等高,圆柱的体积都是圆锥体积的3倍,也就是说在等底等高,圆柱的体积都是圆锥体积的3倍,也就是说在等底等高的情况下圆锥体积是圆柱体积的
。
1
3
是不是所有符合等底等高条件的圆柱、圆锥都具备这样的关系呢?
是的。
总结:
等底等高
圆柱体积等于圆锥体积的3倍
圆锥体积等于圆柱体积的
1
3
你能用字母表示出它们的关系吗?
圆锥体积V=
Sh
1
3
一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V=
Sh=
×19×12=76cm3
1
3
1
3
答:这个零件的体积是76cm3。
巩固新知
课堂练习
通过这节课的学习,你有哪些收获呢?
课堂总结
1.(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积是(
)m3。
(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是(
)m3
。
25.12
423.9
课后练习
2.判断对错,对的画“√”,错的画“×”
。
(1)圆锥的体积等于圆柱体积的
。
(
)
(2)圆柱的体积大于与它等底等高的圆锥的体积。
(
)
(3)圆锥的高是圆柱的高的3倍,它的体积一定相等。
(
)
1
3
×
√
×
再
见
第三单元
第2课时
圆锥的体积(1)
人教版数学六年级下册
学习目标
1.理解圆锥体积公式的推导过程,初步掌握圆锥体积的计算公式,并能运用公式正确地计算圆锥的体积。
2.进行比较、分析、综合、猜测,在感知的基础上加以判断、推理来获取新知识。
同学们,今天我们一起来学习圆锥体积的计算方法。
导入新知
1.开展实验,收集数据。
圆锥的体积究竟和圆柱的体积有什么关系?
这里有沙子和水,还有等底等高和不等底和不等高的各种圆柱、圆锥的模型。
合作探究
实验要求:各组根据需要选用实验用具,小组成员分工合作,轮流操作,作好实验数据的收集整理。
2.分析数据,做出判断。
观察全班实验数据,你发现了什么?
发现大多数情况下圆柱能装下三个圆锥的沙或水,也有两个多或四个等不同结果。
进一步观察分析,什么情况下圆柱刚好能装下三个圆锥的沙或水?
各组互相观察各自的圆柱、圆锥,发现只要是等底等高,圆柱的体积都是圆锥体积的3倍,也就是说在等底等高,圆柱的体积都是圆锥体积的3倍,也就是说在等底等高的情况下圆锥体积是圆柱体积的
。
1
3
是不是所有符合等底等高条件的圆柱、圆锥都具备这样的关系呢?
是的。
总结:
等底等高
圆柱体积等于圆锥体积的3倍
圆锥体积等于圆柱体积的
1
3
你能用字母表示出它们的关系吗?
圆锥体积V=
Sh
1
3
一个圆锥形的零件,底面积是19cm2,高是12cm。这个零件的体积是多少?
V=
Sh=
×19×12=76cm3
1
3
1
3
答:这个零件的体积是76cm3。
巩固新知
课堂练习
通过这节课的学习,你有哪些收获呢?
课堂总结
1.(1)一个圆柱的体积是75.36m3,与它等底等高的圆锥的体积是(
)m3。
(2)一个圆锥的体积是141.3m3,与它等底等高的圆柱的体积是(
)m3
。
25.12
423.9
课后练习
2.判断对错,对的画“√”,错的画“×”
。
(1)圆锥的体积等于圆柱体积的
。
(
)
(2)圆柱的体积大于与它等底等高的圆锥的体积。
(
)
(3)圆锥的高是圆柱的高的3倍,它的体积一定相等。
(
)
1
3
×
√
×
再
见
