人教版数学八年级下册 第18章 平行四边形 分节同步检测题(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级下册 第18章 平行四边形 分节同步检测题(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 355.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 08:06:01 | ||
图片预览




文档简介
18.1平行四边形
一.选择题
1.如图,在?ABCD中,∠A=120°,则∠C的大小为( )
A.60° B.110° C.70° D.120°
2.如图,在△ABC中,AC=8,DE是△ABC的中位线,则DE的长度是( )
A.4 B.5 C.6 D.3
3.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30° B.60° C.90° D.120°
4.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
5.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5 B.5.5 C.6 D.6.5
6.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
7.在平面直角坐标系中,以点O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A. C.
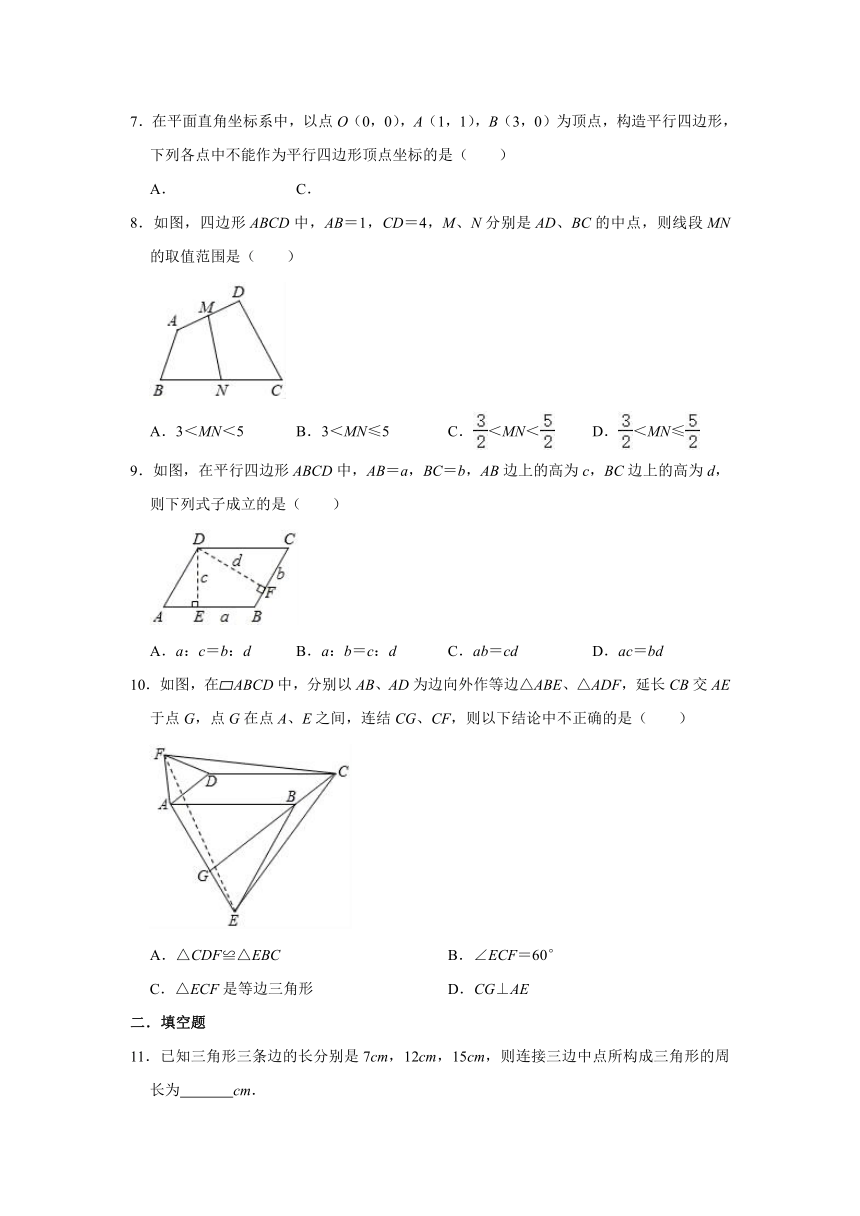
8.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d B.a:b=c:d C.ab=cd D.ac=bd
10.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
二.填空题
11.已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 cm.
12.已知平行四边形ABCD中,E是AB的中点,AB=,AC=3,DE=4,则平行四边形AB边上的高= .
13.如图,平行四边形ABCD的顶点C在等边三角形BEF的边BF上,E点在AB延长线上,G为DE的中点,连结CG,若AD=6,AB=CF=4,则CG的长为 .
14.如图.平行四边形A与平行四边形B部分重叠在一起,重叠部分的面积是A的,是B的,则平行四边形A与平行四边形B的面积比是 .
15.如图,?ABCD中,∠ADC=120°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
三.解答题
16.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.
(1)求证:BM=DN;
(2)求证:四边形AECF为平行四边形.
17.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,判断四边形ABFC的形状,并说明理由.
18.如图,平行四边形ABCD中,分别过A,C两点作AE⊥BD,CF⊥BD,垂足分别为E,F,连接CE,AF.
(1)求证:BE=DF;
(2)若AB=4,EF=,∠AFE=45°,求△ABD的面积.
19.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
参考答案与试题解析
一.选择题
1.【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A=120°,
∴∠C=120°.
故选:D.
2.【解答】解:∵DE是△ABC的中位线,
∴DE=AC=4.
故选:A.
3.【解答】解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
4.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
5.【解答】解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
6.【解答】解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
7.【解答】解:因为经过三点可构造三个平行四边形,即?AOBC1、?ABOC2、?AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选:A.
8.【解答】解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
9.【解答】解:∵AB=a,BC=b,AB边上的高为c,BC边上的高为d,
∴S?ABCD=BCDF=ABDE,即bd=ac,
故选:D.
10.【解答】解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
二.填空题(共5小题)
11.【解答】解:∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),
同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm),
故答案为:17.
12.【解答】解:如图,设AC与DE相交于点O,
∵四边形ABCD是平行四边形,
∴AE∥CD,
∴△AOE∽△COD,
∵E是AB的中点,
∴相似比为1:2,
∴==,
∵AC=3,DE=4,
∴OA=1,OE=,
∵AE=AB==,
∴OA2+OE2=AE2,
∴∠AOE=90°,
∴AC⊥DE,
∵OD=4﹣=,
∴S△ADC=ACOD=4,
∴S平行四边形ABCD=2S△ADC=8,
∵AB=,
∴平行四边形AB边上的高=8÷=.
故答案为:.
13.【解答】解:如图,延长CG交BE于点H,
∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,DC∥AB,
∵AD=6,AB=CF=4,
∴CD=4,BC=6,
∴BF=BC+CF=10,
∵△BEF是等边三角形,G为DE的中点,
∴BF=BE=10,DG=EG,
∵DC∥AB,
∴∠CDG=∠HEG,
在△DCG和△EHG中,
,
∴△DCG≌△EHG(ASA),
∴DC=EH,CG=HG,
∵CD=4,BE=10,
∴HE=4,BH=6,
∵∠CBH=60°,BC=BH=6,
∴△CBH是等边三角形,
∴CH=BC=6,
∴CG=CH=3,
故答案为:3.
14.【解答】解:设重叠部分的面积为a,
∵重叠部分的面积是A的,是B的,
∴平行四边形A的面积为4a,平行四边形B的面积为6a,
∴平行四边形A与平行四边形B的面积比是4a:6a=2:3,
故答案为:2:3.
15.【解答】解:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
∵∠ADC=120°,
∴∠ABC=120°,
∵BE⊥DC,DF⊥BC,CD∥AB,
∴∠BED=90°,∠HFB=90°,∠BED+∠EBA=180°,
∴∠EBA=90°,
∴∠HBF=120°﹣90°=30°,
∴∠BHF=90°﹣30°=60°,
故答案为:60.
三.解答题(共4小题)
16.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AM⊥BC,CN⊥AD,
∴AM∥CN,
∴四边形AMCN为平行四边形,
∴CM=AN,
∴BC﹣CM=AD﹣AN,
即BM=DN;
(2)∵AD∥BC,
∴∠ADB=∠CBD,
∵AM⊥BC,CN⊥AD,
∴∠EMB=∠FND=90°,
在△BME和△DNF中,
,
∴△BME≌△DBF(ASA),
∴EM=DF,
∵四边形AMCN为平行四边形,
∴AM=CN,AM∥CN,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF为平行四边形.
17.【解答】解:四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)解:∵AE⊥BD,∠AFE=45°,
∴△AEF是等腰直角三角形,
∴AE=EF=,
∴BE===,
由(1)得:DF=BE=,
∴BD=BE+EF+DF=2+,
∴△ABD的面积=BD×AE=×(2+)×=+.
19.【解答】解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∴PD=DC﹣PC=12﹣2t,
∴=,
解得t=.
综上所述:t=2s或t=3s或t=s时,点P到四边形ABED相邻两边距离相等.
18.2特殊平行四边形
一.选择题(共10小题)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边平行且相等 B.对角相等
C.对角线互相平分 D.对角线相等
2.下列性质中,矩形具有而菱形不一定具有的是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.邻边相等
3.下列条件中,能判断四边形是菱形的是( )
A.对角线互相垂直且相等的四边形 B.对角线互相垂直的四边形
C.对角线相等的平行四边形 D.对角线互相平分且垂直的四边形
4.要判断一个四边形门框是否为矩形,在下面四个拟定方案中,正确的方案是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
5.若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
6.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,则下面条件能判断平行四边形ABCD是矩形的是( )
A.AC=BD B.AC⊥BD C.AO=CO D.AB=AD
7.如图,△ABC中,∠ACB=90°,AD=DB,CD=4,则AB等于( )
A.8 B.6 C.4 D.2
8.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
9.如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
A.22.5° B.30° C.45° D.67.5°
10.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
二.填空题(共5小题)
11.如图,在△ABC中,∠ACB=90°,CD是△ABC的中线,若∠DCB=40°,则∠A的度数为 °.
12.在矩形ABCD中,对角线AC、BD交于点O,若∠AOB=100°,则∠OAB= .
13.如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是 (只需添加一个即可)
14.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠DEB的度数为 度.
15.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
三.解答题(共5小题)
16.如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
17.在正方形ABCD中,M、N分别是边CD、AD的中点,连接BN,AM交于点E.求证:AM⊥BN.
18.在?ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
19.已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
20.如图,矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发,以每秒一个单位的速度沿A→B→C的方向运动;同时点Q从点B出发,以每秒2个单位的速度沿B→C→D的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为t秒.
(1)当t= 时,两点停止运动;
(2)当t为何值时,△BPQ是等腰三角形?
参考答案
一.选择题(共10小题)
1.解:矩形的性质:对边平行且相等,对角线互相平分且相等;
平行四边形的性质:对边平行且相等,对角线互相平分;
故选项A、B、C不符合题意,D符合题意;
故选:D.
2.解:A、对角线互相垂直是菱形具有的性质,矩形不一定具有,不符合题意;
B、对角线互相平分是菱形和矩形共有的性质,不符合题意;
C、对角线相等是矩形具有的性质,菱形不一定具有,符合题意;
D、邻边相等是菱形具有的性质,矩形不一定具有,不符合题意;
故选:C.
3.解:A、对角线互相垂直相等的四边形不一定是菱形,此选项错误;
B、对角线互相垂直的四边形不一定是菱形,此选项错误;
C、对角线相等的平行四边形也可能是矩形,此选项错误;
D、对角线互相平分且垂直的四边形是菱形,此选项正确;
故选:D.
4.解:∵三个角是直角的四边形是矩形,
∴在下面四个拟定方案中,正确的方案是D,
故选:D.
5.解:如图所示:
∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,AC⊥BD;
故选项B、C、D不符合题意;
∵菱形的对角线不一定相等,
∴AC=BD,不一定成立,
故选项A符合题意;
故选:A.
6.解:A选项是对角线相等,可判定平行四边形ABCD是矩形.而B、C、D不能.
故选:A.
7.解:∵∠ACB=90°,AD=BD,
∴AB=2CD=2×4=8.
故选:A.
8.解:连接AB交OC于点D,
∵四边形ABCD是菱形,
∴AB⊥OC,OD=CD,AD=BD,
∵点C的坐标是(4,0),点B的纵坐标是﹣1,
∴OC=4,BD=AD=1,
∴OD=CD=2,
∴菱形OACB的边长为=.
故选:D.
9.解:∵BE=DB,
∴∠BDE=∠E,
∵∠DBA=∠BDE+∠BED=45°
∴∠BDE=×45°=22.5°.
故选:A.
10.解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.
二.填空题(共5小题)
11.解:∵在△ABC中,∠ACB=90°,CD是△ABC的中线,
∵BD=CD=AB,
∴∠B=∠DCB=40°,
∴∠A=90°﹣∠B=50°,
故答案为:50.
12.解:
∵四边形ABCD是矩形,
∴AC=2OA,BD=2BO,AC=BD,
∴OB=OA,
∵∠AOB=100°,
∴∠OAB=∠OBA=(180°﹣100°)=40°
故答案为:40°.
13.解:条件为∠ABC=90°或AC=BD,
理由是:∵平行四边形ABCD的对角线互相垂直,
∴四边形ABCD是菱形,
∵∠ABC=90°或AC=BD,
∴四边形ABCD是正方形,
故答案为:∠ABC=90°或AC=BD.
14.解:∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∵△ABE是等边三角形
∴AE=AB,∠BAE=∠BEA=60°
∴AD=AE,∠DAE=150°
∴∠AED=∠ADE=(180°﹣∠DAE)=15°
∴∠DEB=∠BEA﹣∠AED=60°﹣15°=45°
故答案为:45.
15.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
三.解答题(共5小题)
16.证明:∵AB∥DC,CE∥DA,
∴四边形ADCE是平行四边形,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
又∵CE∥DA,
∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
17.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAN=∠ADM=90°,
∵M、N分别是边CD、AD的中点,
∴AN=AD,DM=CD,
∴AN=DM,
在△ABN和△DAM中,,
∴△ABN≌△DAM(SAS),
∴∠ABN=∠DAM,
∵∠DAM+∠BAE=90°,
∴∠ABN+∠BAE=90°,
∴∠AEB=90°,
∴AM⊥BN.
18.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.
19.(1)证明:∵DP∥AC,CP∥BD
∴四边形CODP是平行四边形,
∵四边形ABCD是矩形,
∴BD=AC,OD=BD,OC=AC,
∴OD=OC,
∴四边形CODP是菱形;
(2)解:当矩形ABCD的边AD=DC,菱形CODP是正方形,
理由:∵四边形ABCD是矩形,
∴AO=CO,
又∵AD=DC,
∴DO⊥AC,
∴∠DOC=90°,
∴菱形CODP是正方形.
20.解:(1)∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,
∴AB+BC=BC+CD=14,
∵14÷2=7,
∴t=7;
故答案为:7;
(2)由题意得:AP=t,BQ=2t,
分情况讨论:
当0<t≤4时,若BP=BQ,则6﹣t=2t,
∴t=2;
当4<t≤6时,
若PQ=BQ,则PB=2CQ,6﹣t=2(2t﹣8),
∴t=;
当6<t<7时,由题意可知不存在;
综上所述,当t为2或时,△BPQ是等腰三角形.
一.选择题
1.如图,在?ABCD中,∠A=120°,则∠C的大小为( )
A.60° B.110° C.70° D.120°
2.如图,在△ABC中,AC=8,DE是△ABC的中位线,则DE的长度是( )
A.4 B.5 C.6 D.3
3.在平行四边形ABCD中,若∠A=60°,则∠B的度数是( )
A.30° B.60° C.90° D.120°
4.如图,在平行四边形ABCD中,如果EF∥AD,GH∥CD,EF与GH相交于点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
5.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12.若D,E分别为边AC,BC的中点,则DE的长为( )
A.5 B.5.5 C.6 D.6.5
6.下面关于平行四边形的说法中,不正确的是( )
A.对角线互相平分的四边形是平行四边形
B.有一组对边平行,一组对角相等的四边形是平行四边形
C.有一组对边相等,一组对角相等的四边形是平行四边形
D.有两组对角相等的四边形是平行四边形
7.在平面直角坐标系中,以点O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A. C.
8.如图,四边形ABCD中,AB=1,CD=4,M、N分别是AD、BC的中点,则线段MN的取值范围是( )
A.3<MN<5 B.3<MN≤5 C.<MN< D.<MN≤
9.如图,在平行四边形ABCD中,AB=a,BC=b,AB边上的高为c,BC边上的高为d,则下列式子成立的是( )
A.a:c=b:d B.a:b=c:d C.ab=cd D.ac=bd
10.如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下结论中不正确的是( )
A.△CDF≌△EBC B.∠ECF=60°
C.△ECF是等边三角形 D.CG⊥AE
二.填空题
11.已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为 cm.
12.已知平行四边形ABCD中,E是AB的中点,AB=,AC=3,DE=4,则平行四边形AB边上的高= .
13.如图,平行四边形ABCD的顶点C在等边三角形BEF的边BF上,E点在AB延长线上,G为DE的中点,连结CG,若AD=6,AB=CF=4,则CG的长为 .
14.如图.平行四边形A与平行四边形B部分重叠在一起,重叠部分的面积是A的,是B的,则平行四边形A与平行四边形B的面积比是 .
15.如图,?ABCD中,∠ADC=120°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
三.解答题
16.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.
(1)求证:BM=DN;
(2)求证:四边形AECF为平行四边形.
17.如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,判断四边形ABFC的形状,并说明理由.
18.如图,平行四边形ABCD中,分别过A,C两点作AE⊥BD,CF⊥BD,垂足分别为E,F,连接CE,AF.
(1)求证:BE=DF;
(2)若AB=4,EF=,∠AFE=45°,求△ABD的面积.
19.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
参考答案与试题解析
一.选择题
1.【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A=120°,
∴∠C=120°.
故选:D.
2.【解答】解:∵DE是△ABC的中位线,
∴DE=AC=4.
故选:A.
3.【解答】解:如图,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣60°=120°.
故选:D.
4.【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AD∥EF,CD∥GH,
∴AB∥GH∥CD,AD∥EF∥BC,
∴平行四边形有:?ABCD,?ABHG,?CDGH,?BCFE,?ADFE,?AGOE,?BEOH,?OFCH,?OGDF共9个.
即共有9个平行四边形,
故选:D.
5.【解答】解:∵∠C=90°,AC=5,BC=12,
∴AB===13,
∵AD=DC,CE=EB,
∴DE=AB=6.5,
故选:D.
6.【解答】解:A、∵对角线互相平分的四边形是平行四边形,
∴选项A不符合题意;
B、∵有一组对边平行,一组对角相等的四边形是平行四边形,
∴选项B不符合题意;
C、∵有一组对边相等,一组对角相等的四边形不一定是平行四边形,
∴选项C符合题意;
D、∵有两组对角相等的四边形是平行四边形,
∴选项D不符合题意;
故选:C.
7.【解答】解:因为经过三点可构造三个平行四边形,即?AOBC1、?ABOC2、?AOC3B.根据平行四边形的性质,可知B、C、D正好是C1、C2、C3的坐标,
故选:A.
8.【解答】解:连接AC,取AC的中点H,连接MH、NH,
∵M、H分别是AD、AC的中点,
∴MH=CD=2,
同理可得,NH=AB=,
在△MHN中,MH﹣NH<MN<MH+NH,即<MN<,
当H在MN上时,MN=MH+NH=,
∴<MN≤,
故选:D.
9.【解答】解:∵AB=a,BC=b,AB边上的高为c,BC边上的高为d,
∴S?ABCD=BCDF=ABDE,即bd=ac,
故选:D.
10.【解答】解:∵△ABE、△ADF是等边三角形,
∴FD=AD,BE=AB,
∵AD=BC,AB=DC,
∴FD=BC,BE=DC,
∵∠CBE=∠FDC,∠FDA=∠ABE,
∴∠CDF=∠EB,
∴△CDF≌△EBC(SAS),故A正确;
∵∠FAE=∠FAD+∠EAB+∠BAD=60°+60°+(180°﹣∠CDA)=300°﹣∠CDA,
∠FDC=360°﹣∠FDA﹣∠ADC=300°﹣∠CDA,
∴∠CDF=∠EAF,
同理可得:∠CBE=∠EAF=∠CDF,
∵BC=AD=AF,BE=AE,
∴△EAF≌△EBC(SAS),
∴∠AEF=∠BEC,
∵∠AEF+∠FEB=∠BEC+∠FEB=∠AEB=60°,
∴∠FEC=60°,
∵CF=CE,
∴△ECF是等边三角形,故C正确;
∴∠ECF=60°,故B正确;
在等边三角形ABE中,
∵等边三角形顶角平分线、底边上的中线、高和垂直平分线是同一条线段,
∴如果CG⊥AE,则G是AE的中点,
∴∠ABG=30°,∠ABC=150°,
而题目缺少这个条件,
∴CG⊥AE不能求证,故D错误.
故选:D.
二.填空题(共5小题)
11.【解答】解:∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),
同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm),
故答案为:17.
12.【解答】解:如图,设AC与DE相交于点O,
∵四边形ABCD是平行四边形,
∴AE∥CD,
∴△AOE∽△COD,
∵E是AB的中点,
∴相似比为1:2,
∴==,
∵AC=3,DE=4,
∴OA=1,OE=,
∵AE=AB==,
∴OA2+OE2=AE2,
∴∠AOE=90°,
∴AC⊥DE,
∵OD=4﹣=,
∴S△ADC=ACOD=4,
∴S平行四边形ABCD=2S△ADC=8,
∵AB=,
∴平行四边形AB边上的高=8÷=.
故答案为:.
13.【解答】解:如图,延长CG交BE于点H,
∵四边形ABCD是平行四边形,
∴AD=BC,CD=AB,DC∥AB,
∵AD=6,AB=CF=4,
∴CD=4,BC=6,
∴BF=BC+CF=10,
∵△BEF是等边三角形,G为DE的中点,
∴BF=BE=10,DG=EG,
∵DC∥AB,
∴∠CDG=∠HEG,
在△DCG和△EHG中,
,
∴△DCG≌△EHG(ASA),
∴DC=EH,CG=HG,
∵CD=4,BE=10,
∴HE=4,BH=6,
∵∠CBH=60°,BC=BH=6,
∴△CBH是等边三角形,
∴CH=BC=6,
∴CG=CH=3,
故答案为:3.
14.【解答】解:设重叠部分的面积为a,
∵重叠部分的面积是A的,是B的,
∴平行四边形A的面积为4a,平行四边形B的面积为6a,
∴平行四边形A与平行四边形B的面积比是4a:6a=2:3,
故答案为:2:3.
15.【解答】解:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,
∵∠ADC=120°,
∴∠ABC=120°,
∵BE⊥DC,DF⊥BC,CD∥AB,
∴∠BED=90°,∠HFB=90°,∠BED+∠EBA=180°,
∴∠EBA=90°,
∴∠HBF=120°﹣90°=30°,
∴∠BHF=90°﹣30°=60°,
故答案为:60.
三.解答题(共4小题)
16.【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AM⊥BC,CN⊥AD,
∴AM∥CN,
∴四边形AMCN为平行四边形,
∴CM=AN,
∴BC﹣CM=AD﹣AN,
即BM=DN;
(2)∵AD∥BC,
∴∠ADB=∠CBD,
∵AM⊥BC,CN⊥AD,
∴∠EMB=∠FND=90°,
在△BME和△DNF中,
,
∴△BME≌△DBF(ASA),
∴EM=DF,
∵四边形AMCN为平行四边形,
∴AM=CN,AM∥CN,
∴AE=CF,
又∵AE∥CF,
∴四边形AECF为平行四边形.
17.【解答】解:四边形ABFC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
∵E为BC的中点,
∴EB=EC,
在△ABE和△FCE中,
,
∴△ABE≌△FCE(AAS),
∴AB=CF.
∵AB∥CF,
∴四边形ABFC是平行四边形,
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
18.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF;
(2)解:∵AE⊥BD,∠AFE=45°,
∴△AEF是等腰直角三角形,
∴AE=EF=,
∴BE===,
由(1)得:DF=BE=,
∴BD=BE+EF+DF=2+,
∴△ABD的面积=BD×AE=×(2+)×=+.
19.【解答】解:(1)BP=2t=2×3=6,
故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,
∴四边形ABCD是矩形,
∵AD∥BC,
∴∠AFB=∠FBC,
∴∠ABF=∠AFB,
∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,
∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;
故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,
S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,
S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,
S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,
∴点P到AB边的距离也为4,
即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,
∴点P到DE边的距离也为4,
∴PE=DE=5,
∴PC=PE﹣CE=2,
∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,
即PC=PH,
∵PC=2t﹣8,
∴PD=DC﹣PC=12﹣2t,
∴=,
解得t=.
综上所述:t=2s或t=3s或t=s时,点P到四边形ABED相邻两边距离相等.
18.2特殊平行四边形
一.选择题(共10小题)
1.矩形具有而平行四边形不一定具有的性质是( )
A.对边平行且相等 B.对角相等
C.对角线互相平分 D.对角线相等
2.下列性质中,矩形具有而菱形不一定具有的是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.邻边相等
3.下列条件中,能判断四边形是菱形的是( )
A.对角线互相垂直且相等的四边形 B.对角线互相垂直的四边形
C.对角线相等的平行四边形 D.对角线互相平分且垂直的四边形
4.要判断一个四边形门框是否为矩形,在下面四个拟定方案中,正确的方案是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量对角线是否互相垂直 D.测量其中三个角是否是直角
5.若四边形ABCD为菱形,则下列结论中不一定成立的是( )
A.AC=BD B.AC⊥BD C.AB∥CD D.AB=CD
6.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,则下面条件能判断平行四边形ABCD是矩形的是( )
A.AC=BD B.AC⊥BD C.AO=CO D.AB=AD
7.如图,△ABC中,∠ACB=90°,AD=DB,CD=4,则AB等于( )
A.8 B.6 C.4 D.2
8.如图,在直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则菱形OACB的边长为( )
A.3 B. C.5 D.
9.如图,已知四边形ABCD是正方形,E是AB延长线上一点,且BE=BD,则∠BDE的度数是( )
A.22.5° B.30° C.45° D.67.5°
10.如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:
①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.
其中正确的是( )
A.①③ B.①②③④ C.①②③ D.①③④
二.填空题(共5小题)
11.如图,在△ABC中,∠ACB=90°,CD是△ABC的中线,若∠DCB=40°,则∠A的度数为 °.
12.在矩形ABCD中,对角线AC、BD交于点O,若∠AOB=100°,则∠OAB= .
13.如图,平行四边形ABCD的对角线互相垂直,要使ABCD成为正方形,还需添加的一个条件是 (只需添加一个即可)
14.如图,在正方形ABCD的外侧,作等边三角形ABE,则∠DEB的度数为 度.
15.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
三.解答题(共5小题)
16.如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.
17.在正方形ABCD中,M、N分别是边CD、AD的中点,连接BN,AM交于点E.求证:AM⊥BN.
18.在?ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
19.已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,过点C,D分别作BD,AC的平行线,两线相交于点P.
(1)求证:四边形CODP是菱形;
(2)当矩形ABCD的边AD,DC满足什么关系时,菱形CODP是正方形?请说明理由.
20.如图,矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发,以每秒一个单位的速度沿A→B→C的方向运动;同时点Q从点B出发,以每秒2个单位的速度沿B→C→D的方向运动,当其中一点到达终点后两点都停止运动.设两点运动的时间为t秒.
(1)当t= 时,两点停止运动;
(2)当t为何值时,△BPQ是等腰三角形?
参考答案
一.选择题(共10小题)
1.解:矩形的性质:对边平行且相等,对角线互相平分且相等;
平行四边形的性质:对边平行且相等,对角线互相平分;
故选项A、B、C不符合题意,D符合题意;
故选:D.
2.解:A、对角线互相垂直是菱形具有的性质,矩形不一定具有,不符合题意;
B、对角线互相平分是菱形和矩形共有的性质,不符合题意;
C、对角线相等是矩形具有的性质,菱形不一定具有,符合题意;
D、邻边相等是菱形具有的性质,矩形不一定具有,不符合题意;
故选:C.
3.解:A、对角线互相垂直相等的四边形不一定是菱形,此选项错误;
B、对角线互相垂直的四边形不一定是菱形,此选项错误;
C、对角线相等的平行四边形也可能是矩形,此选项错误;
D、对角线互相平分且垂直的四边形是菱形,此选项正确;
故选:D.
4.解:∵三个角是直角的四边形是矩形,
∴在下面四个拟定方案中,正确的方案是D,
故选:D.
5.解:如图所示:
∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,AC⊥BD;
故选项B、C、D不符合题意;
∵菱形的对角线不一定相等,
∴AC=BD,不一定成立,
故选项A符合题意;
故选:A.
6.解:A选项是对角线相等,可判定平行四边形ABCD是矩形.而B、C、D不能.
故选:A.
7.解:∵∠ACB=90°,AD=BD,
∴AB=2CD=2×4=8.
故选:A.
8.解:连接AB交OC于点D,
∵四边形ABCD是菱形,
∴AB⊥OC,OD=CD,AD=BD,
∵点C的坐标是(4,0),点B的纵坐标是﹣1,
∴OC=4,BD=AD=1,
∴OD=CD=2,
∴菱形OACB的边长为=.
故选:D.
9.解:∵BE=DB,
∴∠BDE=∠E,
∵∠DBA=∠BDE+∠BED=45°
∴∠BDE=×45°=22.5°.
故选:A.
10.解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°﹣90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDE﹣S△DEH=S△CDE﹣S△DEH,
即;S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.
二.填空题(共5小题)
11.解:∵在△ABC中,∠ACB=90°,CD是△ABC的中线,
∵BD=CD=AB,
∴∠B=∠DCB=40°,
∴∠A=90°﹣∠B=50°,
故答案为:50.
12.解:
∵四边形ABCD是矩形,
∴AC=2OA,BD=2BO,AC=BD,
∴OB=OA,
∵∠AOB=100°,
∴∠OAB=∠OBA=(180°﹣100°)=40°
故答案为:40°.
13.解:条件为∠ABC=90°或AC=BD,
理由是:∵平行四边形ABCD的对角线互相垂直,
∴四边形ABCD是菱形,
∵∠ABC=90°或AC=BD,
∴四边形ABCD是正方形,
故答案为:∠ABC=90°或AC=BD.
14.解:∵四边形ABCD是正方形
∴AB=AD,∠BAD=90°
∵△ABE是等边三角形
∴AE=AB,∠BAE=∠BEA=60°
∴AD=AE,∠DAE=150°
∴∠AED=∠ADE=(180°﹣∠DAE)=15°
∴∠DEB=∠BEA﹣∠AED=60°﹣15°=45°
故答案为:45.
15.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
三.解答题(共5小题)
16.证明:∵AB∥DC,CE∥DA,
∴四边形ADCE是平行四边形,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
又∵CE∥DA,
∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
17.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠BAN=∠ADM=90°,
∵M、N分别是边CD、AD的中点,
∴AN=AD,DM=CD,
∴AN=DM,
在△ABN和△DAM中,,
∴△ABN≌△DAM(SAS),
∴∠ABN=∠DAM,
∵∠DAM+∠BAE=90°,
∴∠ABN+∠BAE=90°,
∴∠AEB=90°,
∴AM⊥BN.
18.证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.
19.(1)证明:∵DP∥AC,CP∥BD
∴四边形CODP是平行四边形,
∵四边形ABCD是矩形,
∴BD=AC,OD=BD,OC=AC,
∴OD=OC,
∴四边形CODP是菱形;
(2)解:当矩形ABCD的边AD=DC,菱形CODP是正方形,
理由:∵四边形ABCD是矩形,
∴AO=CO,
又∵AD=DC,
∴DO⊥AC,
∴∠DOC=90°,
∴菱形CODP是正方形.
20.解:(1)∵四边形ABCD是矩形,
∴CD=AB=6,BC=AD=8,
∴AB+BC=BC+CD=14,
∵14÷2=7,
∴t=7;
故答案为:7;
(2)由题意得:AP=t,BQ=2t,
分情况讨论:
当0<t≤4时,若BP=BQ,则6﹣t=2t,
∴t=2;
当4<t≤6时,
若PQ=BQ,则PB=2CQ,6﹣t=2(2t﹣8),
∴t=;
当6<t<7时,由题意可知不存在;
综上所述,当t为2或时,△BPQ是等腰三角形.
