人教版七年级下册数学试题:5.2.2平行线的判定练习题(无答案)
文档属性
| 名称 | 人教版七年级下册数学试题:5.2.2平行线的判定练习题(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览

文档简介
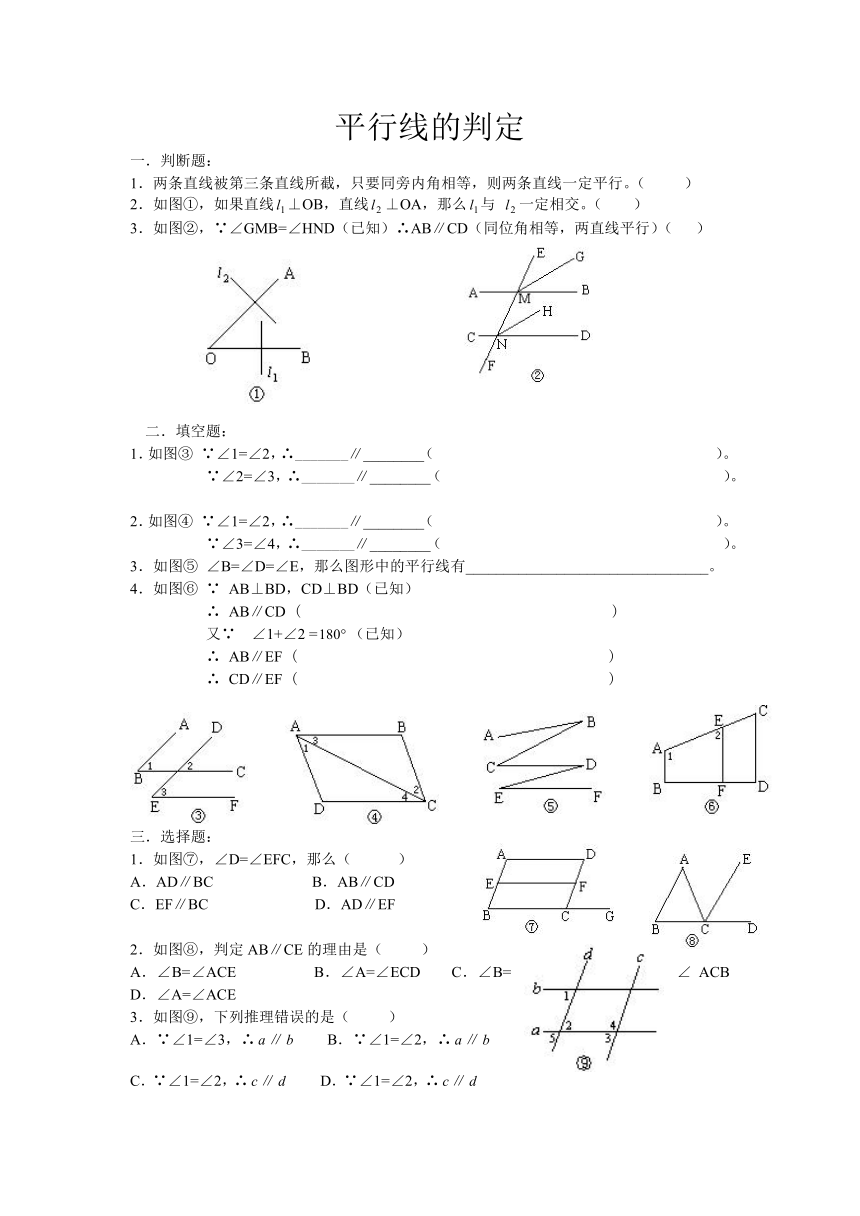
平行线的判定
一.判断题:
1.两条直线被第三条直线所截,只要同旁内角相等,则两条直线一定平行。(
)
2.如图①,如果直线⊥OB,直线⊥OA,那么与
一定相交。(
)
3.如图②,∵∠GMB=∠HND(已知)∴AB∥CD(同位角相等,两直线平行)(
)
二.填空题:
1.如图③
∵∠1=∠2,∴_______∥________(
)。
∵∠2=∠3,∴_______∥________(
)。
2.如图④
∵∠1=∠2,∴_______∥________(
)。
∵∠3=∠4,∴_______∥________(
)。
3.如图⑤
∠B=∠D=∠E,那么图形中的平行线有________________________________。
4.如图⑥
∵
AB⊥BD,CD⊥BD(已知)
∴
AB∥CD
(
)
又∵
∠1+∠2
=(已知)
∴
AB∥EF
(
)
∴
CD∥EF
(
)
三.选择题:
1.如图⑦,∠D=∠EFC,那么(
)
A.AD∥BC
B.AB∥CD
C.EF∥BC
D.AD∥EF
2.如图⑧,判定AB∥CE的理由是(
)
A.∠B=∠ACE
B.∠A=∠ECD
C.∠B=∠ACB
D.∠A=∠ACE
3.如图⑨,下列推理错误的是(
)
A.∵∠1=∠3,∴∥
B.∵∠1=∠2,∴∥
C.∵∠1=∠2,∴∥
D.∵∠1=∠2,∴∥
如图,直线a、b被直线c所截,给出下列条件,①∠1=∠2,②∠3=∠6,
③∠4+∠7=180°,④∠5+∠8=180°其中能判断a∥b的是(
)
①③
B.②④
C.①③④
D.①②③④
四.完成推理,填写推理依据:
1.如图⑩
∵∠B=∠_______,∴
AB∥CD(
)
∵∠BGC=∠_______,∴
CD∥EF(
)
∵AB∥CD
,CD∥EF,
∴
AB∥_______(
)
2.如图⑾
填空:
(1)∵∠2=∠3(已知)
∴
AB__________(
)
(2)∵∠1=∠A(已知)
∴
__________(
)
(3)∵∠1=∠D(已知)
∴
__________(
)
(4)∵_______=∠F(已知)
∴
AC∥DF(
)
3.填空。如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠______=90°(
)
∴∠CAB=∠______(
)
∵∠CAE=∠DBF(已知)
∴∠BAE=∠______
∴_____∥_____(
)
已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°(
)又∠2=∠3(
)
∴∠1+∠3=180°
∴_________(
)
五.证明题
1.已知:如图⑿,CE平分∠ACD,∠1=∠B,
求证:AB∥CE
已知:如图,,,且.
求证:EC∥DF.
一.判断题:
1.两条直线被第三条直线所截,只要同旁内角相等,则两条直线一定平行。(
)
2.如图①,如果直线⊥OB,直线⊥OA,那么与
一定相交。(
)
3.如图②,∵∠GMB=∠HND(已知)∴AB∥CD(同位角相等,两直线平行)(
)
二.填空题:
1.如图③
∵∠1=∠2,∴_______∥________(
)。
∵∠2=∠3,∴_______∥________(
)。
2.如图④
∵∠1=∠2,∴_______∥________(
)。
∵∠3=∠4,∴_______∥________(
)。
3.如图⑤
∠B=∠D=∠E,那么图形中的平行线有________________________________。
4.如图⑥
∵
AB⊥BD,CD⊥BD(已知)
∴
AB∥CD
(
)
又∵
∠1+∠2
=(已知)
∴
AB∥EF
(
)
∴
CD∥EF
(
)
三.选择题:
1.如图⑦,∠D=∠EFC,那么(
)
A.AD∥BC
B.AB∥CD
C.EF∥BC
D.AD∥EF
2.如图⑧,判定AB∥CE的理由是(
)
A.∠B=∠ACE
B.∠A=∠ECD
C.∠B=∠ACB
D.∠A=∠ACE
3.如图⑨,下列推理错误的是(
)
A.∵∠1=∠3,∴∥
B.∵∠1=∠2,∴∥
C.∵∠1=∠2,∴∥
D.∵∠1=∠2,∴∥
如图,直线a、b被直线c所截,给出下列条件,①∠1=∠2,②∠3=∠6,
③∠4+∠7=180°,④∠5+∠8=180°其中能判断a∥b的是(
)
①③
B.②④
C.①③④
D.①②③④
四.完成推理,填写推理依据:
1.如图⑩
∵∠B=∠_______,∴
AB∥CD(
)
∵∠BGC=∠_______,∴
CD∥EF(
)
∵AB∥CD
,CD∥EF,
∴
AB∥_______(
)
2.如图⑾
填空:
(1)∵∠2=∠3(已知)
∴
AB__________(
)
(2)∵∠1=∠A(已知)
∴
__________(
)
(3)∵∠1=∠D(已知)
∴
__________(
)
(4)∵_______=∠F(已知)
∴
AC∥DF(
)
3.填空。如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠______=90°(
)
∴∠CAB=∠______(
)
∵∠CAE=∠DBF(已知)
∴∠BAE=∠______
∴_____∥_____(
)
已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°(
)又∠2=∠3(
)
∴∠1+∠3=180°
∴_________(
)
五.证明题
1.已知:如图⑿,CE平分∠ACD,∠1=∠B,
求证:AB∥CE
已知:如图,,,且.
求证:EC∥DF.
