北师大版 七年级下册 第四章 4.1认识三角形(一)学案(表格式 无答案)
文档属性
| 名称 | 北师大版 七年级下册 第四章 4.1认识三角形(一)学案(表格式 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 351.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 10:27:18 | ||
图片预览




文档简介
认识三角形
学生姓名
性别
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
三角形
教学目标
1.认识三角形的概念及基本要素,并能用符号语言表示三角形及其基本要素教学难点;
2.能正确区分锐角三角形,直角三角形和钝角三角形;
3.理解三角形三边之间的关系,并能用于解决相关的问题;提高自主探究的能力,增强学好数学的信心。
教学重点与难点
重点:认识三角形的概念及基本要素
难点:正确区分锐角三角形,直角三角形和钝角三角形
一、作业检查
作业完成情况:优
良
中
差
内容回顾
回顾上节课内容
知识整理
知识点一、三角形的角
三角形的定义:
(1)由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形。三角形具有稳定性。
如下的图形就是一个三角形。
⑵三角形的内角:三角形的每两条边所组成的角叫做三角形的内角。
在同一个三角形内,大边对大角。
⑶三角形的外角:三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角.
⑷三角形的分类:
注意:每个三角形至少有两个锐角,而至多有一个钝角。
三角形的三个内角中,最大的一个内角是锐角(直角或钝角)时,该三角形即为锐角三角形(直角三角形或钝角三角形)。
2.三角形的各组成部分:
(1)边:组成三角形的三条线段
如右所示:就是三角形的三条边;
(2)顶点:三角形任意两边的交点
如右所示:均为三角形的顶点;
(3)通常情况下,我们用三角形的三个顶点加以一个“△”来表示一个三角形,在表示三角形时,三个字母之间并无顺序关系。如上图中,此三角形可以表示为,△ABC或△BCA_或△BAC。
(4)内角:三角形两边所夹的角,称为三角形的内角,简称角。例如△ABC中,∠A、∠B、∠C都是三角形的内角。
3、三角形内角和:三角形三个内角和等于。
三角形的外角:三角形的外角与相邻的内角互为邻补角,因为每个内角均有两个邻补角,因此三角形共有六个外角,其中有三个与另外三个相等.每个顶点处的两个外角是相等的.
三角形的外角和:每个顶点处取一个外角,再相加,叫三角形的外角和(并非个外角之和)。
三角形的外角和等于。
4、关于三角形角的其他结论:
推论1:
直角三角形的两个锐角互余。
推论2:
三角形的一个外角等于和它不相邻的两个内角的和。
推论3:
三角形的一个外角大于任何一个和它不相邻的内角。
三角形内角和的几种证明方法:
①添加平行线法:
②帕斯卡(法国数学家)折纸法:
③更具动手可行性的剪角法:(不严密)把三角形的三个内角剪下来能拼成一个平角。
5、三角形外角和的证明法:
三角形按最大角的大小来分类:
6、三角形的角与不等式:
1.
若为锐角三角形,则,,;
2.
若为直角三角形,且,则,,
,,。
3.
若为钝角三角形,且,则,,。
巩固提高
例1.
在中,是边上的点,且,的面积是,则的面积是
。
例2.
已知在中,,,则的度数是(
)
A.
B.
C.
D.
例3.
如下图,求的度数。
例4.
如图,求的度数。
例5.
如图所示,已知,,,求度数。
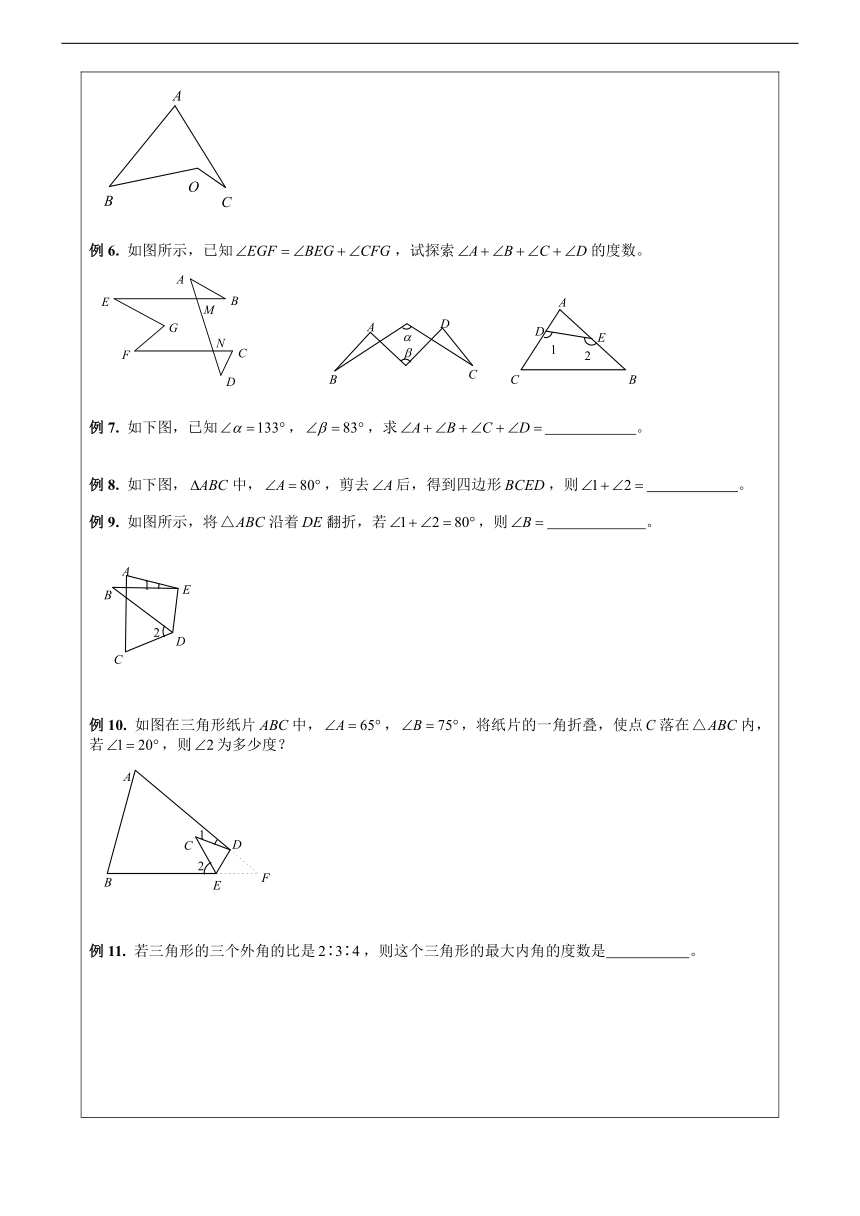
例6.
如图所示,已知,试探索的度数。
例7.
如下图,已知,,求
。
例8.
如下图,中,,剪去后,得到四边形,则
。
例9.
如图所示,将沿着翻折,若,则
。
例10.
如图在三角形纸片中,,,将纸片的一角折叠,使点落在内,若,则为多少度?
例11.
若三角形的三个外角的比是,则这个三角形的最大内角的度数是
。
例12.
如下图所示,在中,,、为上两点,若,,求证:。
知识点二、三角形的边
1、与三角形相关的边
⑴三角形中的三种重要线段
①三角形的角平分线:
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
一个角的平分线与三角形的角平分线的区别是三角形的角平分线是角的顶点到平分线与对边交点
的线段,而角平分线是从角的顶点出发平分角的一条射线
。
如图,若AD是△ABC的角平分线,则∠BAD
=∠CAD=∠BAC或∠BAC=2∠BAD=2∠BAD.
注:每个三角形都有三条角平分线且相交于一点,这个点叫做三角形的内心,而且它一定在三角形内部。
②三角形的中线:
在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线。
如下图,若BE是△ABC中AC边上的中线,则AE=EC=
AC
注:每个三角形都有三条中线,且相交于一点,这个点叫做三角形的中心,而且它一定在三角形内部。
③三角形的高:
从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线。
从三角形一个顶点向它的对边画垂线,以这个顶点和交点为端点的线段叫做三角形边上的高.
如图,若CD是△ABC中AB边上的高,则∠ADC=∠BDC=90°,C点到对边AB的距离是CD的长。
注:每个三角形都有三条高且三条高所在的直线相交于一点,这个点叫做三角形的垂心。
锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部;钝角三角形的高线中有两个垂足落在边的延长线上,这两条高落在三角形的外部,直角三角形有两条高分别与两条直角边重合。反之也成立。画三角形的高时,只需要向对边或对边的延长线作垂线,连接顶点与垂足的线段就是该边的高。
2、三角形三条边的关系
①三角形三边关系:三角形任何两边的和大于第三边。
②三角形三边关系定理的推论:三角形任何两边之差小于第三边。即、、三条线段可组成三角形两条较小的线段之和大于最大的线段。
注意:在应用三边关系定理及推论时,可以简化为:当三条线段中最长的线段小于另两条线段之和时,或当三条线段中最短的线段大于另两条线段之差时,即可组成三角形。
练一练
1、有两根长度分别为4cm和7cm的木棒,
①用长度为2cm的木棒与它们能摆成三角形吗?为什么?
②长度为11cm的木棒呢?
③长度为4cm的木棒呢?
④什么长度范围的木棒,
能与原来的两根木棒摆成三角形.
2、下列各组线段能组成一个三角形的是(
).
(A)3cm,3cm,6cm
(B)2cm,3cm,6cm
(C)5cm,8cm,12cm
(D)4cm,7cm,11cm
3、若三角形的两边长分别为3和5,则其周长l的取值范围是(
).
(A)6<l<15
(B)6<l<16
(C)11<l<13(D)10<l<16
4、若三角形三条边的长分别是7,10,x,求x的范围。
5、下列长度的各组线段能否组成一个三角形?[来源.Com]
(1)15cm、10
cm、7
cm;(2)4
cm、5
cm、10
cm;
(3)3
cm、8
cm、5
cm; (4)4
cm、5
cm、6
cm
巩固提高
1、已知:如图,CE⊥AB于E,AD⊥BC于D,∠A=30°,求∠C的度数.
2、根据所给图形填空:
(1)在ABC中,BC边上的高是________.
(2)在AEC中,AE边上的高是________.
(3)在FEC中,EC边上的高是________.
(4)AB=CD=2cm,AE=3cm。则AEC面积S=_____,CE=_____。
3、已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C-∠B有怎样的数量关系?说明理由
4、下列说法正确的是(
)
A.三角形的角平分线、中线、高都在三角形的内部
B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内
D.钝角三角形的三条高均在三角形外
来源5、如图,
(1)当_____=______时,AD是三角形ABC的中线;
(2)当_____=______时,ED是三角形BEC的角平分线;
(3)当AD⊥BC时,BD是△______的高,又是△______的高。
技能提升
例1.
三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.
2个
B.
3个
C.
4个
D.
5个
例2.
为解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路.现已知这四个村庄及电厂之间的距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线路的最短总长度应该是( )
例3.
为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
例4.
如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依次类推,则第6个图中共有三角形
个。
例5.
下列不能构成三角形三边长的数组是(
)。
A.、、
B.、、
C.、、
D.、、
例6.
一个等腰三角形的两边长分别为和,则它的周长为(
)
A.7
B.9
C.12
D.9或12
例7.
两根木棒的长分别是7和10,要选择第三根木棒,将它们钉成一个三角形,若第三根木棒的长是,则的取值范围是___________。
例8.
已知三角形的三边长分别为、、,则不可能是(
)
A.
B.
C.
D.
例10.
已知三角形两边长为和,求它的周长的取值范围。
例11.
一个三角形三边长分别为,,,则三角形的周长的范围是
。
例12.
已知三角形中两边长为2和7,
(1)若第三边长为奇数,则这个三角形的周长为_________。
(2)若这个三角形的周长为奇数,则第三边长为_________。
例13.
有三条线段,其中两条线段的长为和,第三条线段的长为,若这三条线段不能构成三角形,则的取值范围是
。
例14.
不等边三角形中,如果一条边长等于另两条边长的平均值,那么,最大边上的高与最小边上的高的比值的取值范围是
。
例15.
已知有两边长为、,其中,则其周长一定满足(
)。
A.
B.
C.
D.
例16.
、、为三角形的三边长,化简,若此三角形周长为,求上面式子的值。
例17.
用根火柴棒首尾顺序连接摆成一个三角形,能摆成不同的三角形的个数为
。
例18.
如图,为内一点,试说明。
三、课堂检测
1.下列各组长度的3条线段,不能构成三角形的是(
)
A.3cm
5cm
10cm
B.5cm
5cm
9cm
C.4cm
6cm
9cm
D.2cm
3cm
4cm[来源:学
2.画一个三角形,使它的三条边长分别为3
cm、4
cm、6
cm.
如图,以∠C为内角的三角形有
和
。在这两个三角形中,∠C的对边分别
为
和
。
4.等腰三角形的一边长为3㎝,另一边长是5㎝,则它的第三边长为
。
5、一个等腰三角形的两边长分别是6cm和9cm,则它的周长是
。
7.过直线外一点,如何画这条直线的垂线?你能通过折纸的方法得到这条垂线吗?如何画已知角的角平分线?你能通过折纸的方法得到这个角的角平分线吗?
五、课堂总结
六、课后作业
1.一个三角形的三个内角中
(
)
A
.至少有一个钝角
B
.至少有一个直角
C
.至多有一个锐角
D.
至少有两个锐角
下列长度的三条线段能组成三角形的是(
)
A.
3,4,8
B.
5,6,11
C.
1,2,3
D.
5,6,10
3.
如图在△ABC中,∠ACB=900,CD是边AB上的高。图中与∠A相等的角是(
)
A.∠B
B.
∠ACD
C.∠BCD
D.
∠BDC
4.如图,AC⊥BD,DE⊥AB,下列叙述正确的是()
A.∠A=∠B
B.∠B=∠D
C.∠A=∠D
D.∠A+∠D=900
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的和为(
)
A.180°
B.360°
C.540°
D.720°
6.等腰三角形两边长分别为
3,7,则它的周长为
(
)
A.13
B.
17
C.
13或17
D.
不能确定
7.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,
则∠EDF=________度.
A.58°
B.68°
C.78°
D.32°
8.一个多边形的内角和等于它的外角和,这个多边形是
(
)
A
.三角形
B.四边形
C.
五边形
D.
六边形
能将三角形面积平分的是三角形的()
A.
角平分线
B.高
C.
中线
D.外角平分线
10.如图,AB∥CD,∠A=700,∠B=400,则∠ACD=()
A.
550
B.
700
C.
400
D.
1100
长为11,8,6,4的四根木条,选其中三根组成三角形有种选法,它们分别是________。
一个多边形的内角和是外角和的3倍,它是(
)边形;一个多边形的各内角都等于1200,它是(
)边形。
已知△ABC为等腰三角形,①当它的两个边长分别为8
cm和3
cm时,它的周长为_____;
②如果它的周长为18
cm,一边的长为4
cm,则腰长为_____.
如果一个多边形的每一外角都是240,那么它是几边形?
如图,∠1=∠2=300,∠3=∠4,∠A=800,则_________,______
16.如图飞机要从A地飞往B地,因受大风影响,一开始就偏离航线(AB)18°(即∠A=18°),飞到了C地,已知∠ABC=10°,现在飞机要达到B地需以_____的角飞行(即∠BCD的度数).
如图,△ABC中,高AD与CE的长分别为2㎝,4㎝
求AB与BC的比是多少?
18.如图所示,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
审批
数学科组长
教务主管
校区主任
学生姓名
性别
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
三角形
教学目标
1.认识三角形的概念及基本要素,并能用符号语言表示三角形及其基本要素教学难点;
2.能正确区分锐角三角形,直角三角形和钝角三角形;
3.理解三角形三边之间的关系,并能用于解决相关的问题;提高自主探究的能力,增强学好数学的信心。
教学重点与难点
重点:认识三角形的概念及基本要素
难点:正确区分锐角三角形,直角三角形和钝角三角形
一、作业检查
作业完成情况:优
良
中
差
内容回顾
回顾上节课内容
知识整理
知识点一、三角形的角
三角形的定义:
(1)由三条不在同一条直线上的线段首尾顺次连结组成的平面图形叫做三角形。三角形具有稳定性。
如下的图形就是一个三角形。
⑵三角形的内角:三角形的每两条边所组成的角叫做三角形的内角。
在同一个三角形内,大边对大角。
⑶三角形的外角:三角形的任意一边与另一边的反向延长线所组成的角叫做三角形的外角.
⑷三角形的分类:
注意:每个三角形至少有两个锐角,而至多有一个钝角。
三角形的三个内角中,最大的一个内角是锐角(直角或钝角)时,该三角形即为锐角三角形(直角三角形或钝角三角形)。
2.三角形的各组成部分:
(1)边:组成三角形的三条线段
如右所示:就是三角形的三条边;
(2)顶点:三角形任意两边的交点
如右所示:均为三角形的顶点;
(3)通常情况下,我们用三角形的三个顶点加以一个“△”来表示一个三角形,在表示三角形时,三个字母之间并无顺序关系。如上图中,此三角形可以表示为,△ABC或△BCA_或△BAC。
(4)内角:三角形两边所夹的角,称为三角形的内角,简称角。例如△ABC中,∠A、∠B、∠C都是三角形的内角。
3、三角形内角和:三角形三个内角和等于。
三角形的外角:三角形的外角与相邻的内角互为邻补角,因为每个内角均有两个邻补角,因此三角形共有六个外角,其中有三个与另外三个相等.每个顶点处的两个外角是相等的.
三角形的外角和:每个顶点处取一个外角,再相加,叫三角形的外角和(并非个外角之和)。
三角形的外角和等于。
4、关于三角形角的其他结论:
推论1:
直角三角形的两个锐角互余。
推论2:
三角形的一个外角等于和它不相邻的两个内角的和。
推论3:
三角形的一个外角大于任何一个和它不相邻的内角。
三角形内角和的几种证明方法:
①添加平行线法:
②帕斯卡(法国数学家)折纸法:
③更具动手可行性的剪角法:(不严密)把三角形的三个内角剪下来能拼成一个平角。
5、三角形外角和的证明法:
三角形按最大角的大小来分类:
6、三角形的角与不等式:
1.
若为锐角三角形,则,,;
2.
若为直角三角形,且,则,,
,,。
3.
若为钝角三角形,且,则,,。
巩固提高
例1.
在中,是边上的点,且,的面积是,则的面积是
。
例2.
已知在中,,,则的度数是(
)
A.
B.
C.
D.
例3.
如下图,求的度数。
例4.
如图,求的度数。
例5.
如图所示,已知,,,求度数。
例6.
如图所示,已知,试探索的度数。
例7.
如下图,已知,,求
。
例8.
如下图,中,,剪去后,得到四边形,则
。
例9.
如图所示,将沿着翻折,若,则
。
例10.
如图在三角形纸片中,,,将纸片的一角折叠,使点落在内,若,则为多少度?
例11.
若三角形的三个外角的比是,则这个三角形的最大内角的度数是
。
例12.
如下图所示,在中,,、为上两点,若,,求证:。
知识点二、三角形的边
1、与三角形相关的边
⑴三角形中的三种重要线段
①三角形的角平分线:
三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
一个角的平分线与三角形的角平分线的区别是三角形的角平分线是角的顶点到平分线与对边交点
的线段,而角平分线是从角的顶点出发平分角的一条射线
。
如图,若AD是△ABC的角平分线,则∠BAD
=∠CAD=∠BAC或∠BAC=2∠BAD=2∠BAD.
注:每个三角形都有三条角平分线且相交于一点,这个点叫做三角形的内心,而且它一定在三角形内部。
②三角形的中线:
在三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线。
如下图,若BE是△ABC中AC边上的中线,则AE=EC=
AC
注:每个三角形都有三条中线,且相交于一点,这个点叫做三角形的中心,而且它一定在三角形内部。
③三角形的高:
从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线。
从三角形一个顶点向它的对边画垂线,以这个顶点和交点为端点的线段叫做三角形边上的高.
如图,若CD是△ABC中AB边上的高,则∠ADC=∠BDC=90°,C点到对边AB的距离是CD的长。
注:每个三角形都有三条高且三条高所在的直线相交于一点,这个点叫做三角形的垂心。
锐角三角形的高均在三角形内部,三条高的交点也在三角形的内部;钝角三角形的高线中有两个垂足落在边的延长线上,这两条高落在三角形的外部,直角三角形有两条高分别与两条直角边重合。反之也成立。画三角形的高时,只需要向对边或对边的延长线作垂线,连接顶点与垂足的线段就是该边的高。
2、三角形三条边的关系
①三角形三边关系:三角形任何两边的和大于第三边。
②三角形三边关系定理的推论:三角形任何两边之差小于第三边。即、、三条线段可组成三角形两条较小的线段之和大于最大的线段。
注意:在应用三边关系定理及推论时,可以简化为:当三条线段中最长的线段小于另两条线段之和时,或当三条线段中最短的线段大于另两条线段之差时,即可组成三角形。
练一练
1、有两根长度分别为4cm和7cm的木棒,
①用长度为2cm的木棒与它们能摆成三角形吗?为什么?
②长度为11cm的木棒呢?
③长度为4cm的木棒呢?
④什么长度范围的木棒,
能与原来的两根木棒摆成三角形.
2、下列各组线段能组成一个三角形的是(
).
(A)3cm,3cm,6cm
(B)2cm,3cm,6cm
(C)5cm,8cm,12cm
(D)4cm,7cm,11cm
3、若三角形的两边长分别为3和5,则其周长l的取值范围是(
).
(A)6<l<15
(B)6<l<16
(C)11<l<13(D)10<l<16
4、若三角形三条边的长分别是7,10,x,求x的范围。
5、下列长度的各组线段能否组成一个三角形?[来源.Com]
(1)15cm、10
cm、7
cm;(2)4
cm、5
cm、10
cm;
(3)3
cm、8
cm、5
cm; (4)4
cm、5
cm、6
cm
巩固提高
1、已知:如图,CE⊥AB于E,AD⊥BC于D,∠A=30°,求∠C的度数.
2、根据所给图形填空:
(1)在ABC中,BC边上的高是________.
(2)在AEC中,AE边上的高是________.
(3)在FEC中,EC边上的高是________.
(4)AB=CD=2cm,AE=3cm。则AEC面积S=_____,CE=_____。
3、已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C-∠B有怎样的数量关系?说明理由
4、下列说法正确的是(
)
A.三角形的角平分线、中线、高都在三角形的内部
B.直角三角形只有一条高
C.三角形的三条高至少有一条在三角形内
D.钝角三角形的三条高均在三角形外
来源5、如图,
(1)当_____=______时,AD是三角形ABC的中线;
(2)当_____=______时,ED是三角形BEC的角平分线;
(3)当AD⊥BC时,BD是△______的高,又是△______的高。
技能提升
例1.
三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.
2个
B.
3个
C.
4个
D.
5个
例2.
为解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路.现已知这四个村庄及电厂之间的距离如图所示(距离单位:公里),则能把电力输送到这四个村庄的输电线路的最短总长度应该是( )
例3.
为估计池塘两岸A、B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
例4.
如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依次类推,则第6个图中共有三角形
个。
例5.
下列不能构成三角形三边长的数组是(
)。
A.、、
B.、、
C.、、
D.、、
例6.
一个等腰三角形的两边长分别为和,则它的周长为(
)
A.7
B.9
C.12
D.9或12
例7.
两根木棒的长分别是7和10,要选择第三根木棒,将它们钉成一个三角形,若第三根木棒的长是,则的取值范围是___________。
例8.
已知三角形的三边长分别为、、,则不可能是(
)
A.
B.
C.
D.
例10.
已知三角形两边长为和,求它的周长的取值范围。
例11.
一个三角形三边长分别为,,,则三角形的周长的范围是
。
例12.
已知三角形中两边长为2和7,
(1)若第三边长为奇数,则这个三角形的周长为_________。
(2)若这个三角形的周长为奇数,则第三边长为_________。
例13.
有三条线段,其中两条线段的长为和,第三条线段的长为,若这三条线段不能构成三角形,则的取值范围是
。
例14.
不等边三角形中,如果一条边长等于另两条边长的平均值,那么,最大边上的高与最小边上的高的比值的取值范围是
。
例15.
已知有两边长为、,其中,则其周长一定满足(
)。
A.
B.
C.
D.
例16.
、、为三角形的三边长,化简,若此三角形周长为,求上面式子的值。
例17.
用根火柴棒首尾顺序连接摆成一个三角形,能摆成不同的三角形的个数为
。
例18.
如图,为内一点,试说明。
三、课堂检测
1.下列各组长度的3条线段,不能构成三角形的是(
)
A.3cm
5cm
10cm
B.5cm
5cm
9cm
C.4cm
6cm
9cm
D.2cm
3cm
4cm[来源:学
2.画一个三角形,使它的三条边长分别为3
cm、4
cm、6
cm.
如图,以∠C为内角的三角形有
和
。在这两个三角形中,∠C的对边分别
为
和
。
4.等腰三角形的一边长为3㎝,另一边长是5㎝,则它的第三边长为
。
5、一个等腰三角形的两边长分别是6cm和9cm,则它的周长是
。
7.过直线外一点,如何画这条直线的垂线?你能通过折纸的方法得到这条垂线吗?如何画已知角的角平分线?你能通过折纸的方法得到这个角的角平分线吗?
五、课堂总结
六、课后作业
1.一个三角形的三个内角中
(
)
A
.至少有一个钝角
B
.至少有一个直角
C
.至多有一个锐角
D.
至少有两个锐角
下列长度的三条线段能组成三角形的是(
)
A.
3,4,8
B.
5,6,11
C.
1,2,3
D.
5,6,10
3.
如图在△ABC中,∠ACB=900,CD是边AB上的高。图中与∠A相等的角是(
)
A.∠B
B.
∠ACD
C.∠BCD
D.
∠BDC
4.如图,AC⊥BD,DE⊥AB,下列叙述正确的是()
A.∠A=∠B
B.∠B=∠D
C.∠A=∠D
D.∠A+∠D=900
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的和为(
)
A.180°
B.360°
C.540°
D.720°
6.等腰三角形两边长分别为
3,7,则它的周长为
(
)
A.13
B.
17
C.
13或17
D.
不能确定
7.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,
则∠EDF=________度.
A.58°
B.68°
C.78°
D.32°
8.一个多边形的内角和等于它的外角和,这个多边形是
(
)
A
.三角形
B.四边形
C.
五边形
D.
六边形
能将三角形面积平分的是三角形的()
A.
角平分线
B.高
C.
中线
D.外角平分线
10.如图,AB∥CD,∠A=700,∠B=400,则∠ACD=()
A.
550
B.
700
C.
400
D.
1100
长为11,8,6,4的四根木条,选其中三根组成三角形有种选法,它们分别是________。
一个多边形的内角和是外角和的3倍,它是(
)边形;一个多边形的各内角都等于1200,它是(
)边形。
已知△ABC为等腰三角形,①当它的两个边长分别为8
cm和3
cm时,它的周长为_____;
②如果它的周长为18
cm,一边的长为4
cm,则腰长为_____.
如果一个多边形的每一外角都是240,那么它是几边形?
如图,∠1=∠2=300,∠3=∠4,∠A=800,则_________,______
16.如图飞机要从A地飞往B地,因受大风影响,一开始就偏离航线(AB)18°(即∠A=18°),飞到了C地,已知∠ABC=10°,现在飞机要达到B地需以_____的角飞行(即∠BCD的度数).
如图,△ABC中,高AD与CE的长分别为2㎝,4㎝
求AB与BC的比是多少?
18.如图所示,在△ABC中,∠C-∠B=90°,AE是∠BAC的平分线,求∠AEC的度数.
审批
数学科组长
教务主管
校区主任
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
