北师大版八年级下册数学 1.1 等腰三角形同步练习(Word版 含解析)
文档属性
| 名称 | 北师大版八年级下册数学 1.1 等腰三角形同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 133.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览




文档简介
1.1
等腰三角形
同步测试
一.选择题
1.等腰三角形的周长为20cm,一边长为8cm,那么腰长为( )
A.8cm
B.10cm
C.6cm或8cm
D.12cm或8cm
2.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠BAC=40°,则∠CHD的度数是( )
A.25°
B.35°
C.45°
D.55°
3.如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12
B.13
C.14
D.15
4.如图,在△ABC中,∠BAC=α,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,则∠DAE的大小为( )
A.α
B.
C.
D.α
5.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60°
B.40°、70°
C.50°、60°
D.100°、30°
6.如图所示,在△ABC中,AB=AC,∠A=50°,AB+BC=16cm,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,则△BCF的周长和∠EBF的度数分别等于( )
A.16cm,15°
B.8cm,15°
C.16cm,10°
D.16cm,25°
7.下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
8.如图,在△ABC中,∠C=63°,AD是BC边上的高,∠ABD=45°,点E在AC上,BE交AD于点F,DF=CD,则∠AFB的度数为( )
A.127°
B.117°
C.107°
D.63°
9.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是( )
A.2﹣x
B.3﹣x
C.1
D.2+x
10.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m°
B.180°﹣2m°
C.30°+m°
D.m°
二.填空题
11.边长为6cm的等边三角形的面积是
.
12.等边△ABC周长为9,则△ABC的面积为
.
13.如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8cm,∠B=15°,则AC等于
.
14.如图,在△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠ADE=
.
15.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2,点E为AC上任意一点(不与点A、C重合),连结EB,分别过点A、B作BE、AE的平行线交于点F,则EF的最小值为
.
三.解答题
16.如图,△ABC中BD、CD分别平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F.
(1)若∠A=70°,求∠BDC的度数;
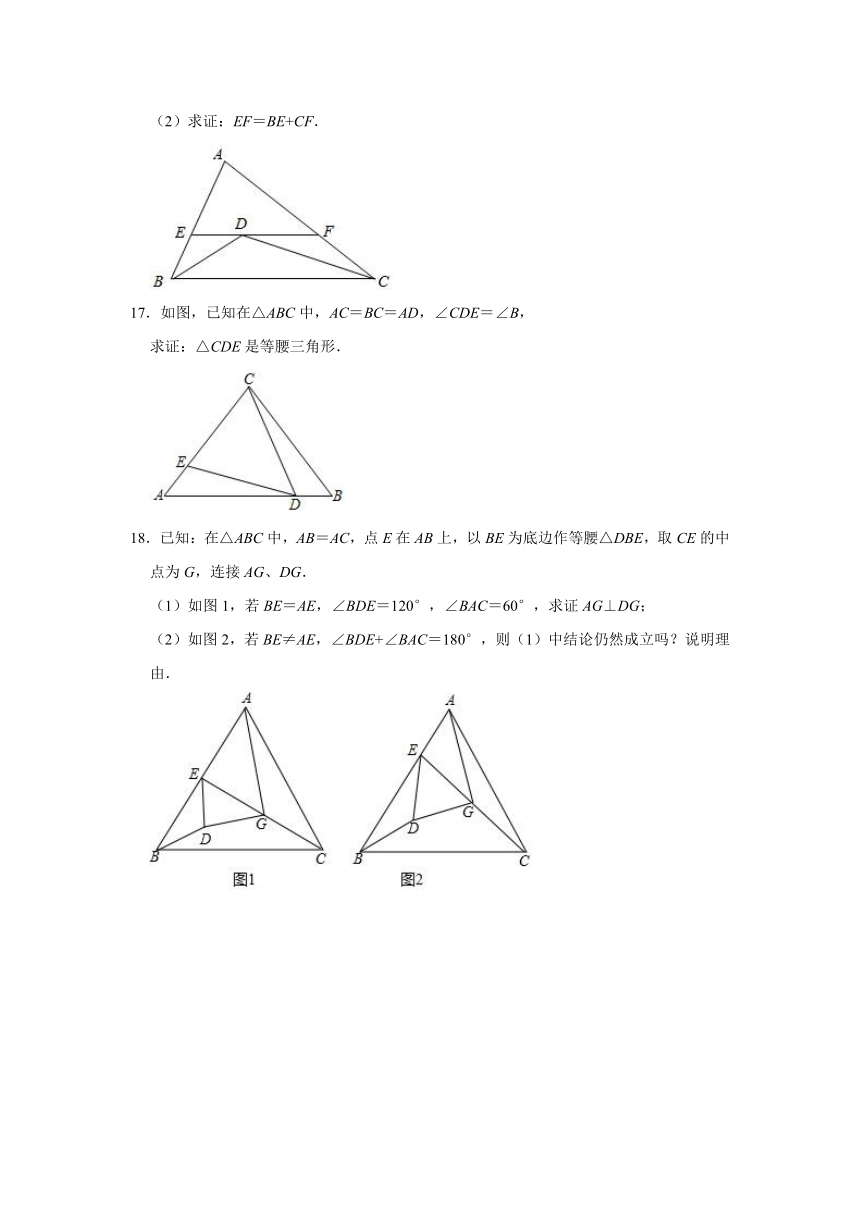
(2)求证:EF=BE+CF.
17.如图,已知在△ABC中,AC=BC=AD,∠CDE=∠B,
求证:△CDE是等腰三角形.
18.已知:在△ABC中,AB=AC,点E在AB上,以BE为底边作等腰△DBE,取CE的中点为G,连接AG、DG.
(1)如图1,若BE=AE,∠BDE=120°,∠BAC=60°,求证AG⊥DG;
(2)如图2,若BE≠AE,∠BDE+∠BAC=180°,则(1)中结论仍然成立吗?说明理由.
参考答案
一.选择题
1.解:∵等腰三角形的周长为20cm,
∴当腰长=6cm时,底边=20﹣8﹣8=4cm,
∴当底边=6cm时,腰长==6cm,
∴腰长为6cm或8cm,
故选:C.
2.解:∵AB=AC,
∴∠B=∠ACB,
∵∠BAC=40°,
∴∠ACB=×(180°﹣40°)=70°,
∵AD是△ABC的中线,
∴AD是△ABC的角平分线,
∴∠CAD=∠BAC=20°,
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°,
∴∠CHD=∠CAD+∠ACE=55°.
故选:D.
3.解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE=8,
∵AB=AD+BD,
∴AB=5+8=13.
故选:B.
4.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,∠DAC=z,
则,
解得y+z=α,
∴∠DAE=∠DAC+∠CAE=;
故选:D.
5.解:A、∵三角形中已知两个内角为30°、60°,
∴第三个内角为180°﹣30°﹣60°=90°,
∴这个三角形是直角三角形,不是等腰三角形,故选项A不符合题意;
B、∵三角形中已知两个内角为40°、70°,
∴第三个内角为180°﹣40°﹣70°=70°,
∴这个三角形由两个内角相等,
∴这个三角形是等腰三角形,故选项B符合题意;
C、∵三角形中已知两个内角为50°、60°,
∴第三个内角为180°﹣50°﹣60°=70°,
∴这个三角形不是等腰三角形,故选项C不符合题意;
D、∵三角形中已知两个内角为100°、30°,
∴第三个内角为180°﹣100°﹣30°=50°,
∴不是等腰三角形,故选项D不符合题意;
故选:B.
6.解:在△ABC中,AB=AC,∠A=50°,
∴∠ABC=∠ACB=65°,
∵DE是AB的垂直平分线,
∴AF=BF,∠BDE=90°,∠ABF=∠A=50°,∠E=25°,
∴∠BFD=90°﹣∠ABF=40°,
∴∠EBF=∠BFD﹣∠E=15°,
∵AB+BC=16cm,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=BC+AB=16(cm).
故选:A.
7.解:图①中,∵∠C=180°﹣∠A﹣∠B=180°﹣70°﹣66°=44°,
∴∠A≠∠B≠∠C,
∴△ABC不是等腰三角形;
图②中,∵∠B+∠C=140°,∠B=70°,
∴∠C=140°﹣70°=70°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图③中,∵AD∥BC,
∴∠C=∠CAD=50°,
∵∠B=50°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图④中,∵AD∥BC,
∴∠BCA=∠CAD=30°,∠BAD=180°﹣∠B=180°﹣120°=60°,
∴∠BAC=60°﹣30°=30°,
∴∠BAC=∠BCA,
∴△ABC是等腰三角形;
图⑤中,∵AB∥DE,
∴∠A=∠D=30°,
∵∠BCD=∠A+∠B=60°,
∴∠B=60°﹣∠A=30°,
∴∠B=∠A,
∴△ABC是等腰三角形;
能判定△ABC是等腰三角形的有4个,
故选:C.
8.解:∵AD是BC边上的高,∠ABD=45°,
∴∠BAD=∠ABD=45°,
∴AD=BD,
∴∠CAD=180°﹣∠C﹣∠BAD﹣∠ABD=180°﹣63°﹣45°﹣45°=27°,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(SAS),
∴∠FBD=∠CAD=27°,
∴∠AFB=∠FBD+∠BDF=27°+90°=117°,
故选:B.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°,
∵PD⊥BC,DE⊥AC,
∴BD=PB,CE=CD,
∵PA=x,
∴BP=4﹣x,
∴BD=PB=2﹣x,
∴CD=4﹣(2﹣x)=2+x,
∴CE=1+x,
∴AE=4﹣(1+x)=3﹣x,
故选:B.
10.解:∵AD垂直平分BE,
∴AB=AE,
∴∠ABE=∠AEB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
∴∠BEC=∠BEA+∠ACE,
∵∠BAC=m°,
∴∠ABC+∠ACB=180°﹣m°,
∴∠BEC=(180°﹣∠ABC﹣∠ACB)=[180°﹣(∠ABC+∠ACB)]=[180°﹣(180°﹣m°)]=m°,
故选:D.
二.填空题
11.解:如图,等边三角形高线即中线,故D为BC中点,
∵AB=6cm,
∴BD=3cm,
∴AD==3,
∴等边△ABC的面积=BC?AD=×6×3=9(cm2).
故答案为:9cm2.
12.解:,
过A作AD⊥BC于D,
∵等边△ABC周长为9,
∴AB=AC=BC=3,
∵AD⊥BC,
∴BD=CD=BC=,
∴AD===,
∴△ABC的面积S===,
故答案为:.
13.解:在△ABC中,∠ACB=90°,∠B=15°,
∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,BE=8cm,
∴BE=AE=8cm,
∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,
∵∠C=90°,
∴∠AEC=30°,
∴AC=AE=×8=4(cm),
故答案是:4cm.
14.解:∵AD=DE,
∴∠DAE=∠DEA,
∵AB=AC,
∴∠B=∠C,设∠B=∠C=x,则∠DAE=∠DEA=∠C+∠EDC=x+10°,
∵∠BAC+∠B+∠C=180°,
∴20°+10°+x+2x=180°,
∴x=50°,
∴∠DAE=∠DEA=60°,
∴∠ADE=60°,
故答案为60°.
15.解:如图,过点B作BH⊥AC于H.
在Rt△ABC中,∵∠ABC=90°,AB=2,∠C=30°,
∴AC=2AB=4,BC=AB?cos30°=2,
∵∠BHC=90°,
∴BH=BC=,
∵BF∥AC,
∵当EF⊥AC时,EF的值最小,最小值=BH=,
故答案为
三.解答题
16.(1)解:∵∠A+∠ABC+∠ACB=180°,∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣70°=110°,
∵BD、CD分别平分∠ABC、∠ACB,
∴∠DBC=∠ABC,∠DCB=ACB,
∴∠DBC+∠DCB=×110°=55°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=125°;
(2)证明:∵BD、CD分别平分∠ABC、∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴BE=DE,CF=DF,
∴EF=DE+DF=BE+CF.
17.证明:∵∠ADE+∠CDE+∠BDC=180°,∠BCD+∠B+∠BDC=180°,∠CDE=∠B,
∴∠ADE=∠BCD,
∵AC=BC,
∴∠A=∠B,
在△ADE和△BCD中,
,
∴△ADE≌△BCD(ASA),
∴DE=CD,
∴△CDE是等腰三角形.
18.(1)证明:延长DG至H,使GH=GD,连接AD,AH,CH,如图1,
∵G为CE的中点,
∴GC=GE,
在△CHG和△EDG中,
,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,
∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,
∴∠ABD=∠ACH,
在△ABD和△ACH中,
,
∴△ABD≌△ACH(SAS),
∴AD=AH,
∵HG=DG,
∴AG⊥DG;
(2)解:(1)中结论仍然成立.
理由:延长DG至M,使GM=GD,连接AD,AM,CM,如图2,
∵G为CE的中点,
∴GC=GE,
在△CMG和△EDG中,
,
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∵BD=ED,
∴∠BED=∠EBD=180°﹣∠BDE,
∵∠BDE+∠BAC=180°,
∴∠BAC=180°﹣∠BDE,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD和△ACM中,
,
∴△ABD≌△ACM(SAS),
∴AD=AM,
∵MG=DG,
∴AG⊥DG.
等腰三角形
同步测试
一.选择题
1.等腰三角形的周长为20cm,一边长为8cm,那么腰长为( )
A.8cm
B.10cm
C.6cm或8cm
D.12cm或8cm
2.如图,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠BAC=40°,则∠CHD的度数是( )
A.25°
B.35°
C.45°
D.55°
3.如图,△ABC中,BE是角平分线,DE∥BC交AB于D,交AC于E,若DE=8,AD=5,则AB等于( )
A.12
B.13
C.14
D.15
4.如图,在△ABC中,∠BAC=α,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,则∠DAE的大小为( )
A.α
B.
C.
D.α
5.在三角形中已知两个内角,能判定这个三角形是等腰三角形的是( )
A.30°、60°
B.40°、70°
C.50°、60°
D.100°、30°
6.如图所示,在△ABC中,AB=AC,∠A=50°,AB+BC=16cm,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,则△BCF的周长和∠EBF的度数分别等于( )
A.16cm,15°
B.8cm,15°
C.16cm,10°
D.16cm,25°
7.下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
8.如图,在△ABC中,∠C=63°,AD是BC边上的高,∠ABD=45°,点E在AC上,BE交AD于点F,DF=CD,则∠AFB的度数为( )
A.127°
B.117°
C.107°
D.63°
9.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是( )
A.2﹣x
B.3﹣x
C.1
D.2+x
10.如图,△ABC中,AB=AC,作△BCE,点A在△BCE内,点D在BE上,AD垂直平分BE,且∠BAC=m°,则∠BEC=( )
A.90°﹣m°
B.180°﹣2m°
C.30°+m°
D.m°
二.填空题
11.边长为6cm的等边三角形的面积是
.
12.等边△ABC周长为9,则△ABC的面积为
.
13.如图所示,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点E,垂足为点D,BE=8cm,∠B=15°,则AC等于
.
14.如图,在△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠ADE=
.
15.如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AB=2,点E为AC上任意一点(不与点A、C重合),连结EB,分别过点A、B作BE、AE的平行线交于点F,则EF的最小值为
.
三.解答题
16.如图,△ABC中BD、CD分别平分∠ABC、∠ACB,过D作直线平行于BC,交AB、AC于E、F.
(1)若∠A=70°,求∠BDC的度数;
(2)求证:EF=BE+CF.
17.如图,已知在△ABC中,AC=BC=AD,∠CDE=∠B,
求证:△CDE是等腰三角形.
18.已知:在△ABC中,AB=AC,点E在AB上,以BE为底边作等腰△DBE,取CE的中点为G,连接AG、DG.
(1)如图1,若BE=AE,∠BDE=120°,∠BAC=60°,求证AG⊥DG;
(2)如图2,若BE≠AE,∠BDE+∠BAC=180°,则(1)中结论仍然成立吗?说明理由.
参考答案
一.选择题
1.解:∵等腰三角形的周长为20cm,
∴当腰长=6cm时,底边=20﹣8﹣8=4cm,
∴当底边=6cm时,腰长==6cm,
∴腰长为6cm或8cm,
故选:C.
2.解:∵AB=AC,
∴∠B=∠ACB,
∵∠BAC=40°,
∴∠ACB=×(180°﹣40°)=70°,
∵AD是△ABC的中线,
∴AD是△ABC的角平分线,
∴∠CAD=∠BAC=20°,
∵CE是△ABC的角平分线,
∴∠ACE=∠ACB=35°,
∴∠CHD=∠CAD+∠ACE=55°.
故选:D.
3.解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∵DE∥BC,
∴∠DEB=∠CBE,
∴∠ABE=∠DEB,
∴BD=DE=8,
∵AB=AD+BD,
∴AB=5+8=13.
故选:B.
4.解:∵AB=BD,AC=CE,
∴∠BAD=∠BDA,∠E=∠CAE,
设∠BAD=∠BDA=x,∠E=∠CAE=y,∠DAC=z,
则,
解得y+z=α,
∴∠DAE=∠DAC+∠CAE=;
故选:D.
5.解:A、∵三角形中已知两个内角为30°、60°,
∴第三个内角为180°﹣30°﹣60°=90°,
∴这个三角形是直角三角形,不是等腰三角形,故选项A不符合题意;
B、∵三角形中已知两个内角为40°、70°,
∴第三个内角为180°﹣40°﹣70°=70°,
∴这个三角形由两个内角相等,
∴这个三角形是等腰三角形,故选项B符合题意;
C、∵三角形中已知两个内角为50°、60°,
∴第三个内角为180°﹣50°﹣60°=70°,
∴这个三角形不是等腰三角形,故选项C不符合题意;
D、∵三角形中已知两个内角为100°、30°,
∴第三个内角为180°﹣100°﹣30°=50°,
∴不是等腰三角形,故选项D不符合题意;
故选:B.
6.解:在△ABC中,AB=AC,∠A=50°,
∴∠ABC=∠ACB=65°,
∵DE是AB的垂直平分线,
∴AF=BF,∠BDE=90°,∠ABF=∠A=50°,∠E=25°,
∴∠BFD=90°﹣∠ABF=40°,
∴∠EBF=∠BFD﹣∠E=15°,
∵AB+BC=16cm,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=BC+AB=16(cm).
故选:A.
7.解:图①中,∵∠C=180°﹣∠A﹣∠B=180°﹣70°﹣66°=44°,
∴∠A≠∠B≠∠C,
∴△ABC不是等腰三角形;
图②中,∵∠B+∠C=140°,∠B=70°,
∴∠C=140°﹣70°=70°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图③中,∵AD∥BC,
∴∠C=∠CAD=50°,
∵∠B=50°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图④中,∵AD∥BC,
∴∠BCA=∠CAD=30°,∠BAD=180°﹣∠B=180°﹣120°=60°,
∴∠BAC=60°﹣30°=30°,
∴∠BAC=∠BCA,
∴△ABC是等腰三角形;
图⑤中,∵AB∥DE,
∴∠A=∠D=30°,
∵∠BCD=∠A+∠B=60°,
∴∠B=60°﹣∠A=30°,
∴∠B=∠A,
∴△ABC是等腰三角形;
能判定△ABC是等腰三角形的有4个,
故选:C.
8.解:∵AD是BC边上的高,∠ABD=45°,
∴∠BAD=∠ABD=45°,
∴AD=BD,
∴∠CAD=180°﹣∠C﹣∠BAD﹣∠ABD=180°﹣63°﹣45°﹣45°=27°,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(SAS),
∴∠FBD=∠CAD=27°,
∴∠AFB=∠FBD+∠BDF=27°+90°=117°,
故选:B.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°,
∵PD⊥BC,DE⊥AC,
∴BD=PB,CE=CD,
∵PA=x,
∴BP=4﹣x,
∴BD=PB=2﹣x,
∴CD=4﹣(2﹣x)=2+x,
∴CE=1+x,
∴AE=4﹣(1+x)=3﹣x,
故选:B.
10.解:∵AD垂直平分BE,
∴AB=AE,
∴∠ABE=∠AEB,
∵AB=AC,
∴AE=AC,
∴∠AEC=∠ACE,
∴∠BEC=∠BEA+∠ACE,
∵∠BAC=m°,
∴∠ABC+∠ACB=180°﹣m°,
∴∠BEC=(180°﹣∠ABC﹣∠ACB)=[180°﹣(∠ABC+∠ACB)]=[180°﹣(180°﹣m°)]=m°,
故选:D.
二.填空题
11.解:如图,等边三角形高线即中线,故D为BC中点,
∵AB=6cm,
∴BD=3cm,
∴AD==3,
∴等边△ABC的面积=BC?AD=×6×3=9(cm2).
故答案为:9cm2.
12.解:,
过A作AD⊥BC于D,
∵等边△ABC周长为9,
∴AB=AC=BC=3,
∵AD⊥BC,
∴BD=CD=BC=,
∴AD===,
∴△ABC的面积S===,
故答案为:.
13.解:在△ABC中,∠ACB=90°,∠B=15°,
∴∠BAC=90°﹣15°=75°,
∵DE垂直平分AB,BE=8cm,
∴BE=AE=8cm,
∴∠EAB=∠B=15°,
∴∠EAC=75°﹣15°=60°,
∵∠C=90°,
∴∠AEC=30°,
∴AC=AE=×8=4(cm),
故答案是:4cm.
14.解:∵AD=DE,
∴∠DAE=∠DEA,
∵AB=AC,
∴∠B=∠C,设∠B=∠C=x,则∠DAE=∠DEA=∠C+∠EDC=x+10°,
∵∠BAC+∠B+∠C=180°,
∴20°+10°+x+2x=180°,
∴x=50°,
∴∠DAE=∠DEA=60°,
∴∠ADE=60°,
故答案为60°.
15.解:如图,过点B作BH⊥AC于H.
在Rt△ABC中,∵∠ABC=90°,AB=2,∠C=30°,
∴AC=2AB=4,BC=AB?cos30°=2,
∵∠BHC=90°,
∴BH=BC=,
∵BF∥AC,
∵当EF⊥AC时,EF的值最小,最小值=BH=,
故答案为
三.解答题
16.(1)解:∵∠A+∠ABC+∠ACB=180°,∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣70°=110°,
∵BD、CD分别平分∠ABC、∠ACB,
∴∠DBC=∠ABC,∠DCB=ACB,
∴∠DBC+∠DCB=×110°=55°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=125°;
(2)证明:∵BD、CD分别平分∠ABC、∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴BE=DE,CF=DF,
∴EF=DE+DF=BE+CF.
17.证明:∵∠ADE+∠CDE+∠BDC=180°,∠BCD+∠B+∠BDC=180°,∠CDE=∠B,
∴∠ADE=∠BCD,
∵AC=BC,
∴∠A=∠B,
在△ADE和△BCD中,
,
∴△ADE≌△BCD(ASA),
∴DE=CD,
∴△CDE是等腰三角形.
18.(1)证明:延长DG至H,使GH=GD,连接AD,AH,CH,如图1,
∵G为CE的中点,
∴GC=GE,
在△CHG和△EDG中,
,
∴△CHG≌△EDG(SAS),
∴CH=ED,∠HCG=∠DEG,
∵BD=ED,∠BDE=120°,
∴∠BED=∠EBD=30°,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∵AE=BE,
∴CE⊥AB,
∴∠BED+∠DEG=90°,∠BAC+∠ACE=90°,
∴∠HCG=∠DEG=60°,∠ACE=30°,
∴∠ACH=30°,
∴∠ABD=∠ACH,
在△ABD和△ACH中,
,
∴△ABD≌△ACH(SAS),
∴AD=AH,
∵HG=DG,
∴AG⊥DG;
(2)解:(1)中结论仍然成立.
理由:延长DG至M,使GM=GD,连接AD,AM,CM,如图2,
∵G为CE的中点,
∴GC=GE,
在△CMG和△EDG中,
,
∴△CMG≌△EDG(SAS),
∴CM=ED,∠MCG=∠DEG,
∵BD=ED,
∴∠BED=∠EBD=180°﹣∠BDE,
∵∠BDE+∠BAC=180°,
∴∠BAC=180°﹣∠BDE,
∴∠BAC=2∠BED=2∠EBD,
∵∠BEC=∠BED+∠DEG=∠BAC+∠ACE,
∴∠BED+∠MCG=∠BAC+∠ACE,
∵∠MCG=∠ACM+∠ACE,
∴∠BED+∠ACM+∠ACE=2∠BED+∠ACE,
∴∠ACM=∠BED=∠ABD,
在△ABD和△ACM中,
,
∴△ABD≌△ACM(SAS),
∴AD=AM,
∵MG=DG,
∴AG⊥DG.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
