人教 版数学九年级下册28.2例3和例4 测量——的仰角、俯角教案
文档属性
| 名称 | 人教 版数学九年级下册28.2例3和例4 测量——的仰角、俯角教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 128.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览

文档简介
《解直角三角形应用举例(1)教案》
【学习目标】
1、了解仰角、俯角和方向角的命名特点,将实际问题转化为解直角三角形的问题,
选用适当的锐角三角函数解决方向角问题.
2、渗透数形结合的数学思想和方法,逐步培养分析问题、解决问题的能力.
【学习重点】
恰当运用三角函数有关知识解决实际问题
【学习难点】
学会准确分析问题并将实际问题转化成数学模型
1、在直角三角形中,____________
____________________________叫解直角三角形.
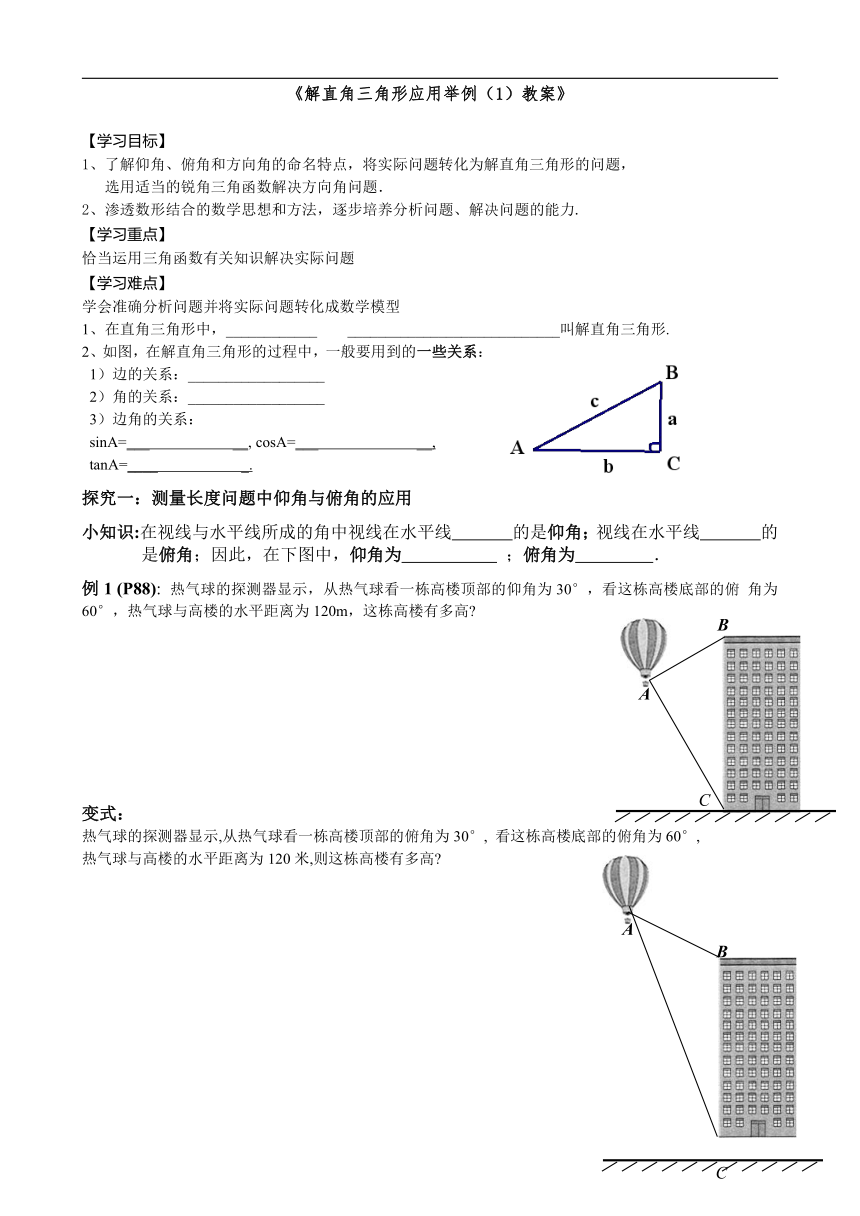
2、如图,在解直角三角形的过程中,一般要用到的一些关系:
1)边的关系:__________________
2)角的关系:__________________
3)边角的关系:
sinA=___
__,
cosA=___
__,
tanA=____
_.
探究一:测量长度问题中仰角与俯角的应用
小知识:在视线与水平线所成的角中视线在水平线
的是仰角;视线在水平线
的是俯角;因此,在下图中,仰角为
;俯角为
.
例1
(P88):
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯
角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?
变式:
热气球的探测器显示,从热气球看一栋高楼顶部的俯角为30°,
看这栋高楼底部的俯角为60°,
热气球与高楼的水平距离为120米,则这栋高楼有多高?
探究二:航海问题中方向角的应用
问题二:如图,一艘海轮位于灯塔P的北偏东60方向,距离灯塔海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东33方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(sin33°≈0.545,cos33°≈0.839)
【课堂练习】
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角60°,
观察底部B的仰角为45°,求旗杆的高度.
2.如图,海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛在北偏东30°向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?说明理由。
【归纳小结】
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
【作业】《解直角三角形应用举例(1)》
【学习目标】
1、了解仰角、俯角和方向角的命名特点,将实际问题转化为解直角三角形的问题,
选用适当的锐角三角函数解决方向角问题.
2、渗透数形结合的数学思想和方法,逐步培养分析问题、解决问题的能力.
【学习重点】
恰当运用三角函数有关知识解决实际问题
【学习难点】
学会准确分析问题并将实际问题转化成数学模型
1、在直角三角形中,____________
____________________________叫解直角三角形.
2、如图,在解直角三角形的过程中,一般要用到的一些关系:
1)边的关系:__________________
2)角的关系:__________________
3)边角的关系:
sinA=___
__,
cosA=___
__,
tanA=____
_.
探究一:测量长度问题中仰角与俯角的应用
小知识:在视线与水平线所成的角中视线在水平线
的是仰角;视线在水平线
的是俯角;因此,在下图中,仰角为
;俯角为
.
例1
(P88):
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯
角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?
变式:
热气球的探测器显示,从热气球看一栋高楼顶部的俯角为30°,
看这栋高楼底部的俯角为60°,
热气球与高楼的水平距离为120米,则这栋高楼有多高?
探究二:航海问题中方向角的应用
问题二:如图,一艘海轮位于灯塔P的北偏东60方向,距离灯塔海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东33方向上的B处.这时,海轮所在的B处距离灯塔P有多远?(sin33°≈0.545,cos33°≈0.839)
【课堂练习】
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角60°,
观察底部B的仰角为45°,求旗杆的高度.
2.如图,海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛在北偏东30°向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?说明理由。
【归纳小结】
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
【作业】《解直角三角形应用举例(1)》
