人教版七年级下册数学课时作业:5.3.1 平行线的性质(word版,含答案)
文档属性
| 名称 | 人教版七年级下册数学课时作业:5.3.1 平行线的性质(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 158.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 13:05:27 | ||
图片预览


文档简介
5.3.1 平行线的性质
知识点
1 两直线平行,同位角相等
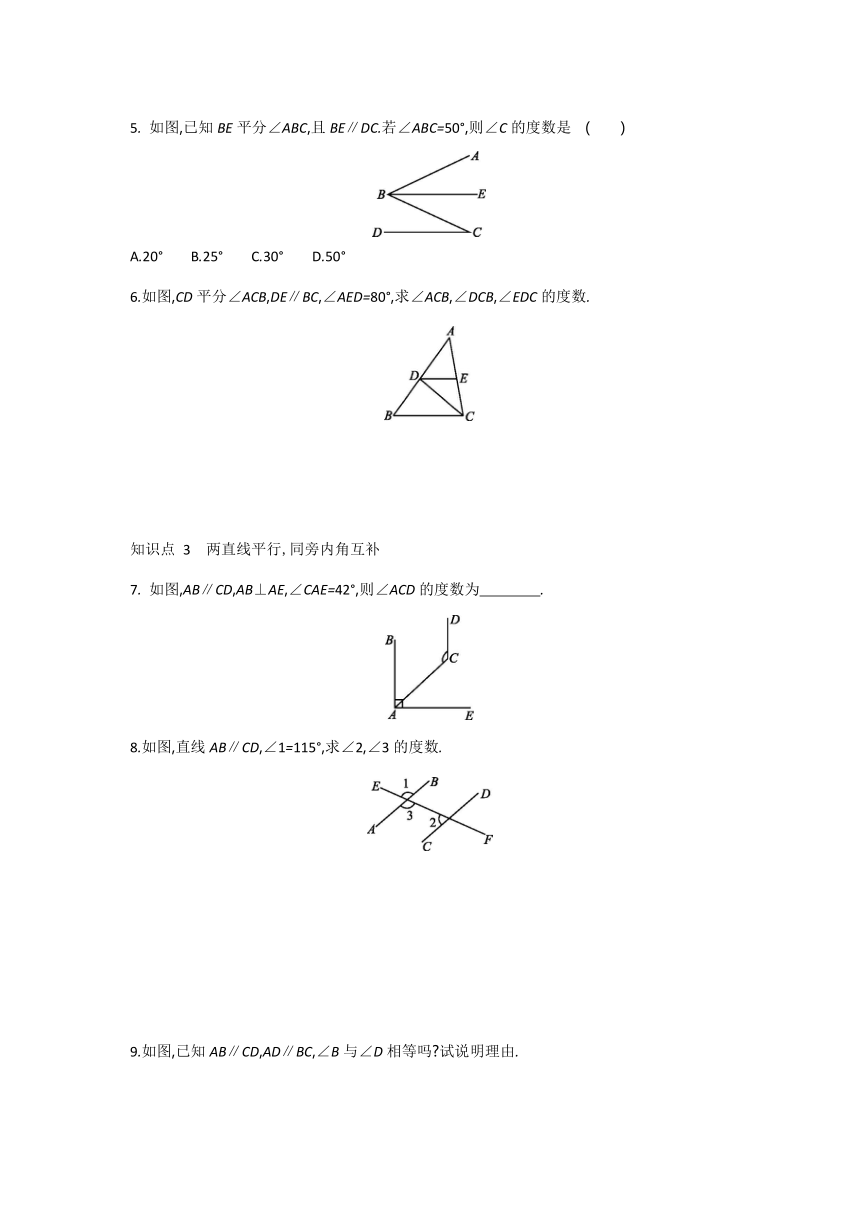
1.如图,已知a∥b,∠1=58°,则∠2的度数是
( )
A.122°
B.85°
C.58°
D.32°
2.
如图,直线a∥b,∠1=50°,则∠2的度数为
( )
A.40°
B.50°
C.55°
D.60°
3.如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,求∠1的度数.
知识点
2 两直线平行,内错角相等
4.如图所示,直线l1,l2被直线l3所截,且l1∥l2,则∠α的度数为
( )
A.41°
B.49°
C.51°
D.59°
5.
如图,已知BE平分∠ABC,且BE∥DC.若∠ABC=50°,则∠C的度数是
( )
A.20°
B.25°
C.30°
D.50°
6.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB,∠DCB,∠EDC的度数.
知识点
3 两直线平行,同旁内角互补
7.
如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 .?
8.如图,直线AB∥CD,∠1=115°,求∠2,∠3的度数.
9.如图,已知AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.
10.
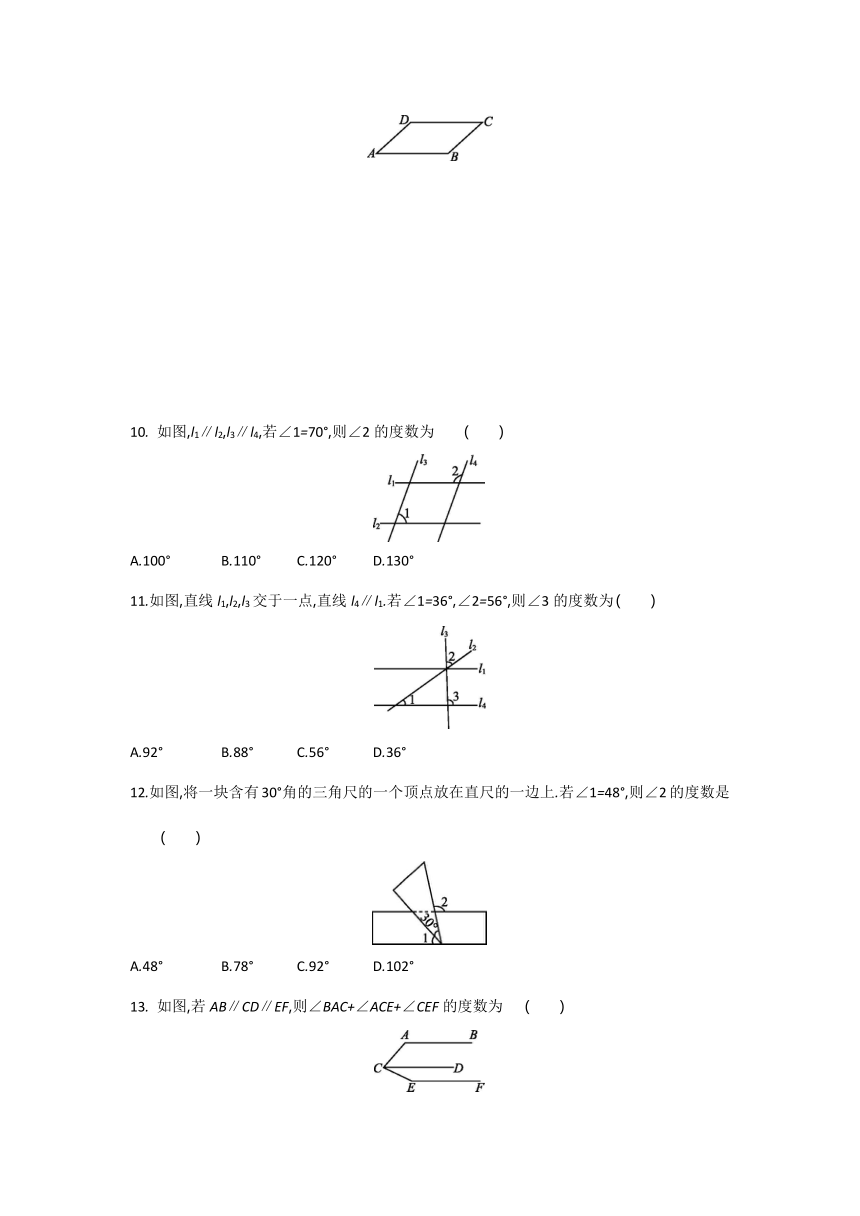
如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为
( )
A.100°
B.110°
C.120°
D.130°
11.如图,直线l1,l2,l3交于一点,直线l4∥l1.若∠1=36°,∠2=56°,则∠3的度数为
( )
A.92°
B.88°
C.56°
D.36°
12.如图,将一块含有30°角的三角尺的一个顶点放在直尺的一边上.若∠1=48°,则∠2的度数是
( )
A.48°
B.78°
C.92°
D.102°
13.
如图,若AB∥CD∥EF,则∠BAC+∠ACE+∠CEF的度数为
( )
A.360°
B.270°
C.180°
D.无法确定
14.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE= °.?
15.如图,AB∥CD,E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
16.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
17.我们已经判定条件与相关性质.涉及同位角、内错角、同旁内角.如图①,在“三线八角”中,类比内错角,具有∠1与∠8这样位置关系的角称为“外错角”,试完成下面的探究问题.
(1)探究定义:如图①,请另找出一对“外错角”: .?
(2)猜想判定:外错角相等,两直线平行.
如图②,∠1与∠2是直线a,b被直线c截出的一对外错角,且∠1=∠2,试说明:a∥b.
(3)猜想性质:两直线平行,外错角相等.
如图②,∠1与∠2是直线a,b被直线c截出的一对外错角,且a∥b,试说明:∠1=∠2.
参考答案
1.C 2.B
3.解:∵AB∥EF,
∴∠A=∠2=50°.
∵AC∥DF,
∴∠1=∠A=50°.
4.B 5.B
6.解:∵DE∥BC,
∴∠ACB=∠AED=80°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=40°.
∵DE∥BC,
∴∠EDC=∠DCB=40°.
7.132°
8.解:∵∠1=115°,∴∠3=∠1=115°.
∵AB∥CD,
∴∠2+∠3=180°,
∴∠2=65°.
9.解:∠B=∠D.理由如下:
∵AB∥CD,
∴∠D+∠A=180°(两直线平行,同旁内角互补).
∵AD∥BC,
∴∠B+∠A=180°(两直线平行,同旁内角互补),
∴∠B=∠D(同角的补角相等).
10.B 解析:
∵l1∥l2,∠1=70°,
∴∠3=∠1=70°.
∵l3∥l4,
∴∠2=180°-∠3=180°-70°=110°.
故选B.
11.A 12.D
13.A
14.20 解析:
∵AB∥EF∥CD,
∴∠BCD=∠ABC=46°,∠CEF+∠DCE=180°.
∵∠CEF=154°,
∴∠DCE=180°-∠CEF=180°-154°=26°,
∴∠BCE=∠BCD-∠DCE=46°-26°=20°.
15.解:∵∠AEC=42°,
∴∠AED=180°-∠AEC=138°.
∵EF平分∠AED,
∴∠DEF=∠AED=69°.
∵AB∥CD,∴∠AFE=∠DEF=69°.
16.解:因为EF∥AD,所以∠1=∠BAD.
又因为∠1=∠2,所以∠2=∠BAD,
所以AB∥DG,
所以∠BAC+∠AGD=180°.
因为∠BAC=70°,所以∠AGD=110°.
17.解:(1)∠2和∠7
(2)∵∠1=∠3,∠1=∠2,∴∠2=∠3,
∴a∥b(同位角相等,两直线平行).
(3)∵a∥b,
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠3,
∴∠1=∠2.
知识点
1 两直线平行,同位角相等
1.如图,已知a∥b,∠1=58°,则∠2的度数是
( )
A.122°
B.85°
C.58°
D.32°
2.
如图,直线a∥b,∠1=50°,则∠2的度数为
( )
A.40°
B.50°
C.55°
D.60°
3.如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上.若∠2=50°,求∠1的度数.
知识点
2 两直线平行,内错角相等
4.如图所示,直线l1,l2被直线l3所截,且l1∥l2,则∠α的度数为
( )
A.41°
B.49°
C.51°
D.59°
5.
如图,已知BE平分∠ABC,且BE∥DC.若∠ABC=50°,则∠C的度数是
( )
A.20°
B.25°
C.30°
D.50°
6.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ACB,∠DCB,∠EDC的度数.
知识点
3 两直线平行,同旁内角互补
7.
如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 .?
8.如图,直线AB∥CD,∠1=115°,求∠2,∠3的度数.
9.如图,已知AB∥CD,AD∥BC,∠B与∠D相等吗?试说明理由.
10.
如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为
( )
A.100°
B.110°
C.120°
D.130°
11.如图,直线l1,l2,l3交于一点,直线l4∥l1.若∠1=36°,∠2=56°,则∠3的度数为
( )
A.92°
B.88°
C.56°
D.36°
12.如图,将一块含有30°角的三角尺的一个顶点放在直尺的一边上.若∠1=48°,则∠2的度数是
( )
A.48°
B.78°
C.92°
D.102°
13.
如图,若AB∥CD∥EF,则∠BAC+∠ACE+∠CEF的度数为
( )
A.360°
B.270°
C.180°
D.无法确定
14.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE= °.?
15.如图,AB∥CD,E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
16.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
17.我们已经判定条件与相关性质.涉及同位角、内错角、同旁内角.如图①,在“三线八角”中,类比内错角,具有∠1与∠8这样位置关系的角称为“外错角”,试完成下面的探究问题.
(1)探究定义:如图①,请另找出一对“外错角”: .?
(2)猜想判定:外错角相等,两直线平行.
如图②,∠1与∠2是直线a,b被直线c截出的一对外错角,且∠1=∠2,试说明:a∥b.
(3)猜想性质:两直线平行,外错角相等.
如图②,∠1与∠2是直线a,b被直线c截出的一对外错角,且a∥b,试说明:∠1=∠2.
参考答案
1.C 2.B
3.解:∵AB∥EF,
∴∠A=∠2=50°.
∵AC∥DF,
∴∠1=∠A=50°.
4.B 5.B
6.解:∵DE∥BC,
∴∠ACB=∠AED=80°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=40°.
∵DE∥BC,
∴∠EDC=∠DCB=40°.
7.132°
8.解:∵∠1=115°,∴∠3=∠1=115°.
∵AB∥CD,
∴∠2+∠3=180°,
∴∠2=65°.
9.解:∠B=∠D.理由如下:
∵AB∥CD,
∴∠D+∠A=180°(两直线平行,同旁内角互补).
∵AD∥BC,
∴∠B+∠A=180°(两直线平行,同旁内角互补),
∴∠B=∠D(同角的补角相等).
10.B 解析:
∵l1∥l2,∠1=70°,
∴∠3=∠1=70°.
∵l3∥l4,
∴∠2=180°-∠3=180°-70°=110°.
故选B.
11.A 12.D
13.A
14.20 解析:
∵AB∥EF∥CD,
∴∠BCD=∠ABC=46°,∠CEF+∠DCE=180°.
∵∠CEF=154°,
∴∠DCE=180°-∠CEF=180°-154°=26°,
∴∠BCE=∠BCD-∠DCE=46°-26°=20°.
15.解:∵∠AEC=42°,
∴∠AED=180°-∠AEC=138°.
∵EF平分∠AED,
∴∠DEF=∠AED=69°.
∵AB∥CD,∴∠AFE=∠DEF=69°.
16.解:因为EF∥AD,所以∠1=∠BAD.
又因为∠1=∠2,所以∠2=∠BAD,
所以AB∥DG,
所以∠BAC+∠AGD=180°.
因为∠BAC=70°,所以∠AGD=110°.
17.解:(1)∠2和∠7
(2)∵∠1=∠3,∠1=∠2,∴∠2=∠3,
∴a∥b(同位角相等,两直线平行).
(3)∵a∥b,
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠3,
∴∠1=∠2.
