人教版数学九年级下册:28.2.1 解直角三角形教案
文档属性
| 名称 | 人教版数学九年级下册:28.2.1 解直角三角形教案 | 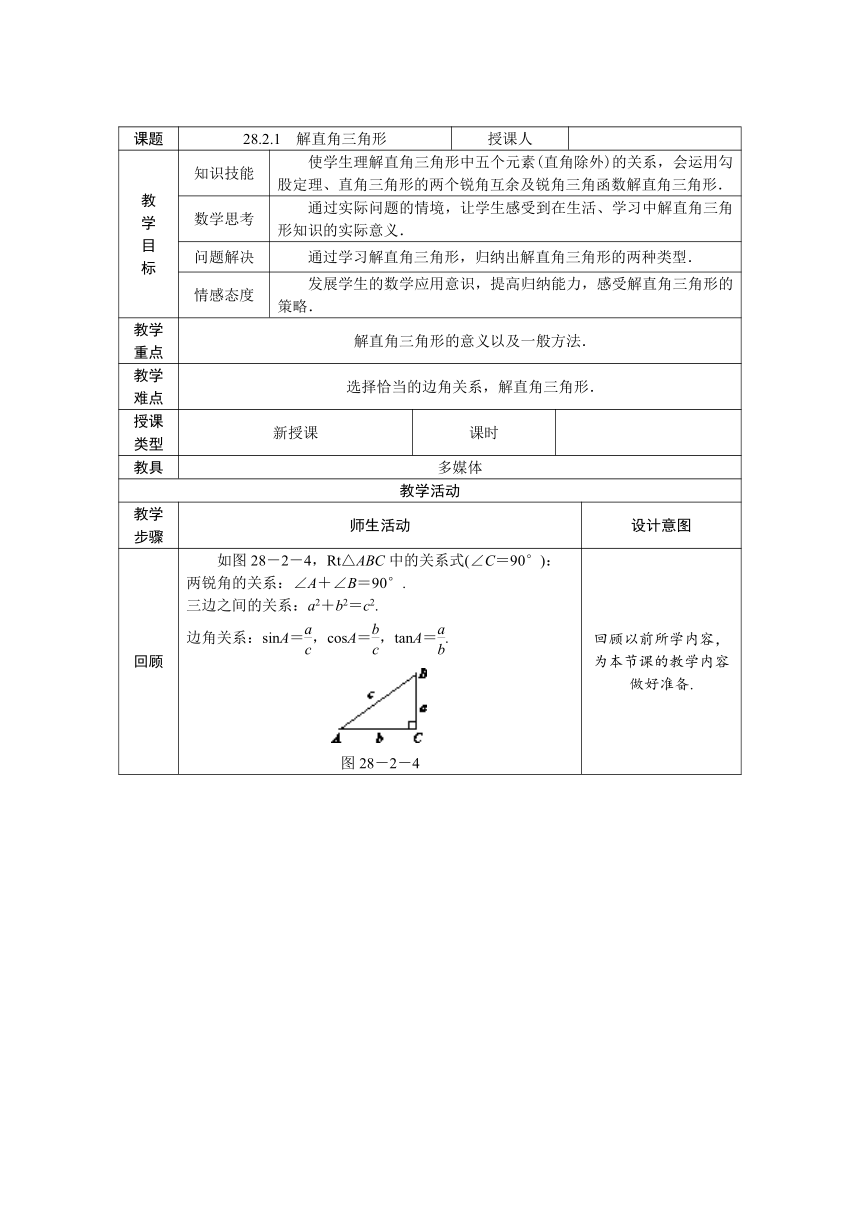 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 14:43:02 | ||
图片预览



文档简介
课题
28.2.1 解直角三角形
授课人
教
学
目
标
知识技能
使学生理解直角三角形中五个元素(直角除外)的关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
数学思考
通过实际问题的情境,让学生感受到在生活、学习中解直角三角形知识的实际意义.
问题解决
通过学习解直角三角形,归纳出解直角三角形的两种类型.
情感态度
发展学生的数学应用意识,提高归纳能力,感受解直角三角形的策略.
教学
重点
解直角三角形的意义以及一般方法.
教学
难点
选择恰当的边角关系,解直角三角形.
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
回顾
如图28-2-4,Rt△ABC中的关系式(∠C=90°):
两锐角的关系:∠A+∠B=90°.
三边之间的关系:a2+b2=c2.
边角关系:sinA=,cosA=,tanA=.
图28-2-4
回顾以前所学内容,为本节课的教学内容做好准备.
(续表)
活动
一:
创设
情境
导入
新课
【课堂引入】
意大利比萨斜塔在落成时就已倾斜,其塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为C,如图28-2-5.在Rt△ABC中,∠C=90°,BC=5.2
m,AB=54.5
m,求∠A的度数.
图28-2-5
师生活动:教师呈现问题并引导学生结合图形,观察已知和所求角之间的关系,分析得到通过求∠A的正弦来求∠A的度数.
通过实际问题,激发学生的学习兴趣,把实际问题转化为数学问题,通过求解,初步体会解直角三角形的内涵,引入课题.
活动
二:
实践
探究
交流
新知
1.解直角三角形的定义
问题:将比萨斜塔问题推广为一般的数学问题该如何求解?
师生活动:已知直角三角形的斜边和一条直角边,求它的锐角的度数,利用锐角的正弦(或余弦)的概念直接求解.
问题:在活动一所述的Rt△ABC中,你还能求出其他未知的边和角吗?
师生活动:学生思考并说明求解思路,教师把问题一般化,给出解直角三角形的内涵:
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
2.解直角三角形的方法
问题:回想一下,刚才解直角三角形的过程中,用到了哪些知识?你能梳理一下直角三角形各个元素之间的关系吗?
师生活动:如图28-2-6,引导学生结合图形,梳理五个元素(直角除外)之间的关系,学生展示:
(1)三边之间的关系:a2+b2=c2(勾股定理).
(2)两锐角之间的关系:∠A+∠B=90°.
(3)边角之间的关系:
图28-2-6
sinA=,cosA=,tanA=,
sinB=,cosB=,tanB=.
问题:从上述问题来看,在直角三角形中,知道斜边和一条直角边这两个元素,可以求出其余的三个元素.一般地,已知五个元素(直角除外)中的任意两个元素,可以求其余元素吗?
教师给出结论:在直角三角形中,知道除直角外的五个元素中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
1.有条理地梳理直角三角形五个元素之间的关系,明确各自的作用,便于应用.
2.在讨论解直角三角形的方法过程中,明确解直角三角形的条件,培养学生的逻辑思维能力.
(续表)
活动
三:
开放
训练
体现
应用
【应用举例】
例1 教材P73例1
如图28-2-7,在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
师生活动:学生在教师的引导下,思考如
图28-2-7
何求出所有未知元素.先让学生找出所有未知元素:∠A,∠B和AB,然后让学生逐一说明求每一个未知元素的方法和依据,教师引导学生选择简便的解题途径.
通过解特殊的直角三角形,训练学生解直角三角形的思路和方法,提高学生分析和解决问题的能力.
【拓展提升】
1.涉“斜”选“弦”的策略
当已知和所求涉及直角三角形的斜边时,应选择与斜边相关的已知角的正弦、余弦.我们把它叫做涉“斜”(涉及斜边)选“弦”(选正弦、余弦)的策略.
例2 滨州中考在Rt△ABC中,∠C=90°,AB=10,sinA=,cosA=,tanA=,则BC的长为(A)
A.6 B.7.5 C.8 D.12.5
2.无“斜”选“切”的策略
当已知和所求均未涉及到斜边时,应选择与斜边无关的边角关系式——正切,这种方法称之为无“斜”(斜边)选“切”(正切)的策略.
例3 在Rt△ABC中,∠C=90°,若∠A=60°,AC=20
m,则BC大约是(结果精确到0.1
m)(B)
A.34.64
m
B.34.6
m
C.28.3
m
D.17.3
m
进一步训练学生解一般直角三角形的思路和方法,并学会从计算简便的角度选用适当的关系式求解.
活动
四:
课堂
总结
反思
【达标测评】
1.在Rt△ABC中,∠C=90°,∠B=40°,BC=3,则AC=(C)
A.3sin40° B.3sin50° C.3tan40° D.3tan50°
2.在Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长为(B)
A.3
B.4
C.5
D.6
3.在△ABC中,若∠C=90°,sinA=,AB=2,则△ABC的周长为__3+__.
4.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为__或或或__.
5.如图28-2-8,在△ABC中,BD⊥AC,AB=6,AC=5
,∠A=30°.
(1)求BD和AD的长;
图28-2-8
(2)求tanC的值.
通过设置达标测评,进一步巩固所学新知,同时检测学习效果,做到“堂堂清”.
(续表)
活动
四:
课堂
总结
反思
1.课堂总结:
请同学们回顾以下问题:
(1)什么叫解直角三角形?
(2)两个直角三角形全等要具备什么条件?为什么在直角三角形中,已知一边和一个锐角或两边就能解直角三角形呢?
2.布置作业:
教材第77页习题28.2第1题.
引导学生从知识和方法两个方面总结自己的收获,理清解直角三角形的目的、条件、依据、方法,提升综合运用知识的能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在创设情境中,由一个实际问题引入,自然过渡到直角三角形.在探究新知中,采用启发法、讨论法等教学方法,学生通过讨论、实践形成理论体系,对知识掌握较为牢固.
②[讲授效果反思]
解直角三角形是重点,而选择恰当的边角关系则是难点,为了突破此难点,本节课选择了两个例题让学生探究、讨论、总结出选择边角关系的策略:涉“斜”选“弦”,无“斜”选“切”,避“除”就“乘”,能“正”不“余”.
因为有这些例题的引导,所以学生对于解直角三角形的两个类型的掌握,应该没有问题,建议把补充练习也安排给成绩中等及以上的学生.
③[师生互动反思]
_____________________________________________
_____________________________________________
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步提升操作流程和自身素质.
典案二 导学设计
【学习目标】
1.知识技能
(1)掌握直角三角形的边角关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
(2)
理解解一个直角三角形的前提条件.
2.解决问题
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
3.数学思考
让学生思考:为什么一个直角三角形可以解的前提条件是必须有两个元素(其中一个必须为边).从而让学生理解画一个直角三角形的条件.
4.情感态度
(1)
通过给定具体的两个条件(其中一个为边),让学生们画直角三角形,培养学生合作交流的意识和探索精神.
(2)通过本节的学习,向学生渗透数形结合的数学思想,培养他们良好的学习习惯.
【学习重难点】
重点:直角三角形的解法.
难点:
(1)三角函数在解直角三角形中的灵活运用.
(2)学生可能不理解在已知的两个元素中,为什么至少有一个是边.
课前延伸
【知识梳理】
(1)
在Rt△ABC中,∠C=90°,a=3,c=4,则b=____.
(2)
在Rt△ABC中,∠C=90°,∠A=28°,那么∠B=__62°__.
(3)
在Rt△ABC中,∠C=90°,a=4,b=5,则sinA=____,cosA=____,tan
A=____
(4)
在Rt△ABC中,∠C=90°,
∠A=30°,a=6,则c=__12__,b=__6__.
(5)
在Rt△ABC中,∠C=90°,已知c=6,
∠A=50°,则a=__6_sin50°__.
(6)
意大利披萨斜塔在建成的时候就已倾斜,其塔顶中心点偏离垂直中心线2.1米,1972年披萨地区发生地震,这座高54.5米的斜塔在大幅摇摆后依然屹立,但塔顶中心点偏离垂直中心线增至5.2米,请你算出这时塔身中心线与垂直中心线的夹角.
课内探究
一、
课堂探究1(问题探究,自主学习)
(1)在Rt△ABC中,∠C=90°,c=28,
∠B=60°,解这个直角三角形.
(2)在Rt△ACB中,c=90°,a=30,
∠B=80°,
解这个直角三角形.
(3)在Rt△ABC中,c=90°,a=3,b=3,
解这个直角三角形.
二、
课堂探究2(分组讨论,合作探究)
(1)
画一个直角三角形,使两条直角边分别为3和4.
(2)
画一个直角三角形,使一条直角边为3,一个锐角为35°.
(3)
画一个直角三角形,使斜边长为8,一个锐角为40°.
(4)
画一个直角三角形,使两个锐角分别为30°和60°.
各小组比较由(1)(2)(3)(4)画出的直角三角形.
讨论1:你觉得给出什么样的条件可以画出一个确定的三角形.
讨论2:你觉得确定一个直角三角形需要的元素有什么条件?
三、
反馈训练
1.必做题
在Rt△ABC中,∠C=90°,已知b=20,
∠B=35°,
解这个直角三角形(结果保留小数);
(2)在Rt△ABC中,∠C=90°,已知a=10
,b=20,
解这个直角三角形.
2.选做题
在Rt△ABC中,∠C=90°,AC=15,
∠A的平分线AD=10
,解这个直角三角形.
课后提升
1.
在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
2.
已知在△ABC中,∠B=60°,∠C=45°,AB=6,求BC长.
3.
如图,在两面墙之间有一个底端在点A的梯子,当它靠在一侧墙上时,梯子的顶端在点B处;当它靠在另一侧墙上时,梯子的顶端在点D处.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3
m.求点B到地面的垂直距离BC.
图28-2-9
28.2.1 解直角三角形
授课人
教
学
目
标
知识技能
使学生理解直角三角形中五个元素(直角除外)的关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
数学思考
通过实际问题的情境,让学生感受到在生活、学习中解直角三角形知识的实际意义.
问题解决
通过学习解直角三角形,归纳出解直角三角形的两种类型.
情感态度
发展学生的数学应用意识,提高归纳能力,感受解直角三角形的策略.
教学
重点
解直角三角形的意义以及一般方法.
教学
难点
选择恰当的边角关系,解直角三角形.
授课
类型
新授课
课时
教具
多媒体
教学活动
教学
步骤
师生活动
设计意图
回顾
如图28-2-4,Rt△ABC中的关系式(∠C=90°):
两锐角的关系:∠A+∠B=90°.
三边之间的关系:a2+b2=c2.
边角关系:sinA=,cosA=,tanA=.
图28-2-4
回顾以前所学内容,为本节课的教学内容做好准备.
(续表)
活动
一:
创设
情境
导入
新课
【课堂引入】
意大利比萨斜塔在落成时就已倾斜,其塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠A,过点B向垂直中心线引垂线,垂足为C,如图28-2-5.在Rt△ABC中,∠C=90°,BC=5.2
m,AB=54.5
m,求∠A的度数.
图28-2-5
师生活动:教师呈现问题并引导学生结合图形,观察已知和所求角之间的关系,分析得到通过求∠A的正弦来求∠A的度数.
通过实际问题,激发学生的学习兴趣,把实际问题转化为数学问题,通过求解,初步体会解直角三角形的内涵,引入课题.
活动
二:
实践
探究
交流
新知
1.解直角三角形的定义
问题:将比萨斜塔问题推广为一般的数学问题该如何求解?
师生活动:已知直角三角形的斜边和一条直角边,求它的锐角的度数,利用锐角的正弦(或余弦)的概念直接求解.
问题:在活动一所述的Rt△ABC中,你还能求出其他未知的边和角吗?
师生活动:学生思考并说明求解思路,教师把问题一般化,给出解直角三角形的内涵:
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
2.解直角三角形的方法
问题:回想一下,刚才解直角三角形的过程中,用到了哪些知识?你能梳理一下直角三角形各个元素之间的关系吗?
师生活动:如图28-2-6,引导学生结合图形,梳理五个元素(直角除外)之间的关系,学生展示:
(1)三边之间的关系:a2+b2=c2(勾股定理).
(2)两锐角之间的关系:∠A+∠B=90°.
(3)边角之间的关系:
图28-2-6
sinA=,cosA=,tanA=,
sinB=,cosB=,tanB=.
问题:从上述问题来看,在直角三角形中,知道斜边和一条直角边这两个元素,可以求出其余的三个元素.一般地,已知五个元素(直角除外)中的任意两个元素,可以求其余元素吗?
教师给出结论:在直角三角形中,知道除直角外的五个元素中的两个元素(至少有一个是边),就可以求出其余三个未知元素.
1.有条理地梳理直角三角形五个元素之间的关系,明确各自的作用,便于应用.
2.在讨论解直角三角形的方法过程中,明确解直角三角形的条件,培养学生的逻辑思维能力.
(续表)
活动
三:
开放
训练
体现
应用
【应用举例】
例1 教材P73例1
如图28-2-7,在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
师生活动:学生在教师的引导下,思考如
图28-2-7
何求出所有未知元素.先让学生找出所有未知元素:∠A,∠B和AB,然后让学生逐一说明求每一个未知元素的方法和依据,教师引导学生选择简便的解题途径.
通过解特殊的直角三角形,训练学生解直角三角形的思路和方法,提高学生分析和解决问题的能力.
【拓展提升】
1.涉“斜”选“弦”的策略
当已知和所求涉及直角三角形的斜边时,应选择与斜边相关的已知角的正弦、余弦.我们把它叫做涉“斜”(涉及斜边)选“弦”(选正弦、余弦)的策略.
例2 滨州中考在Rt△ABC中,∠C=90°,AB=10,sinA=,cosA=,tanA=,则BC的长为(A)
A.6 B.7.5 C.8 D.12.5
2.无“斜”选“切”的策略
当已知和所求均未涉及到斜边时,应选择与斜边无关的边角关系式——正切,这种方法称之为无“斜”(斜边)选“切”(正切)的策略.
例3 在Rt△ABC中,∠C=90°,若∠A=60°,AC=20
m,则BC大约是(结果精确到0.1
m)(B)
A.34.64
m
B.34.6
m
C.28.3
m
D.17.3
m
进一步训练学生解一般直角三角形的思路和方法,并学会从计算简便的角度选用适当的关系式求解.
活动
四:
课堂
总结
反思
【达标测评】
1.在Rt△ABC中,∠C=90°,∠B=40°,BC=3,则AC=(C)
A.3sin40° B.3sin50° C.3tan40° D.3tan50°
2.在Rt△ABC中,∠C=90°,若AB=5,sinA=,则AC的长为(B)
A.3
B.4
C.5
D.6
3.在△ABC中,若∠C=90°,sinA=,AB=2,则△ABC的周长为__3+__.
4.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为__或或或__.
5.如图28-2-8,在△ABC中,BD⊥AC,AB=6,AC=5
,∠A=30°.
(1)求BD和AD的长;
图28-2-8
(2)求tanC的值.
通过设置达标测评,进一步巩固所学新知,同时检测学习效果,做到“堂堂清”.
(续表)
活动
四:
课堂
总结
反思
1.课堂总结:
请同学们回顾以下问题:
(1)什么叫解直角三角形?
(2)两个直角三角形全等要具备什么条件?为什么在直角三角形中,已知一边和一个锐角或两边就能解直角三角形呢?
2.布置作业:
教材第77页习题28.2第1题.
引导学生从知识和方法两个方面总结自己的收获,理清解直角三角形的目的、条件、依据、方法,提升综合运用知识的能力.
【知识网络】
提纲挈领,重点突出.
【教学反思】
①[授课流程反思]
在创设情境中,由一个实际问题引入,自然过渡到直角三角形.在探究新知中,采用启发法、讨论法等教学方法,学生通过讨论、实践形成理论体系,对知识掌握较为牢固.
②[讲授效果反思]
解直角三角形是重点,而选择恰当的边角关系则是难点,为了突破此难点,本节课选择了两个例题让学生探究、讨论、总结出选择边角关系的策略:涉“斜”选“弦”,无“斜”选“切”,避“除”就“乘”,能“正”不“余”.
因为有这些例题的引导,所以学生对于解直角三角形的两个类型的掌握,应该没有问题,建议把补充练习也安排给成绩中等及以上的学生.
③[师生互动反思]
_____________________________________________
_____________________________________________
④[习题反思]
好题题号
错题题号
反思教学过程和教师表现,进一步提升操作流程和自身素质.
典案二 导学设计
【学习目标】
1.知识技能
(1)掌握直角三角形的边角关系,会运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
(2)
理解解一个直角三角形的前提条件.
2.解决问题
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
3.数学思考
让学生思考:为什么一个直角三角形可以解的前提条件是必须有两个元素(其中一个必须为边).从而让学生理解画一个直角三角形的条件.
4.情感态度
(1)
通过给定具体的两个条件(其中一个为边),让学生们画直角三角形,培养学生合作交流的意识和探索精神.
(2)通过本节的学习,向学生渗透数形结合的数学思想,培养他们良好的学习习惯.
【学习重难点】
重点:直角三角形的解法.
难点:
(1)三角函数在解直角三角形中的灵活运用.
(2)学生可能不理解在已知的两个元素中,为什么至少有一个是边.
课前延伸
【知识梳理】
(1)
在Rt△ABC中,∠C=90°,a=3,c=4,则b=____.
(2)
在Rt△ABC中,∠C=90°,∠A=28°,那么∠B=__62°__.
(3)
在Rt△ABC中,∠C=90°,a=4,b=5,则sinA=____,cosA=____,tan
A=____
(4)
在Rt△ABC中,∠C=90°,
∠A=30°,a=6,则c=__12__,b=__6__.
(5)
在Rt△ABC中,∠C=90°,已知c=6,
∠A=50°,则a=__6_sin50°__.
(6)
意大利披萨斜塔在建成的时候就已倾斜,其塔顶中心点偏离垂直中心线2.1米,1972年披萨地区发生地震,这座高54.5米的斜塔在大幅摇摆后依然屹立,但塔顶中心点偏离垂直中心线增至5.2米,请你算出这时塔身中心线与垂直中心线的夹角.
课内探究
一、
课堂探究1(问题探究,自主学习)
(1)在Rt△ABC中,∠C=90°,c=28,
∠B=60°,解这个直角三角形.
(2)在Rt△ACB中,c=90°,a=30,
∠B=80°,
解这个直角三角形.
(3)在Rt△ABC中,c=90°,a=3,b=3,
解这个直角三角形.
二、
课堂探究2(分组讨论,合作探究)
(1)
画一个直角三角形,使两条直角边分别为3和4.
(2)
画一个直角三角形,使一条直角边为3,一个锐角为35°.
(3)
画一个直角三角形,使斜边长为8,一个锐角为40°.
(4)
画一个直角三角形,使两个锐角分别为30°和60°.
各小组比较由(1)(2)(3)(4)画出的直角三角形.
讨论1:你觉得给出什么样的条件可以画出一个确定的三角形.
讨论2:你觉得确定一个直角三角形需要的元素有什么条件?
三、
反馈训练
1.必做题
在Rt△ABC中,∠C=90°,已知b=20,
∠B=35°,
解这个直角三角形(结果保留小数);
(2)在Rt△ABC中,∠C=90°,已知a=10
,b=20,
解这个直角三角形.
2.选做题
在Rt△ABC中,∠C=90°,AC=15,
∠A的平分线AD=10
,解这个直角三角形.
课后提升
1.
在Rt△ABC中,∠C=90°,AC=,BC=,解这个直角三角形.
2.
已知在△ABC中,∠B=60°,∠C=45°,AB=6,求BC长.
3.
如图,在两面墙之间有一个底端在点A的梯子,当它靠在一侧墙上时,梯子的顶端在点B处;当它靠在另一侧墙上时,梯子的顶端在点D处.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3
m.求点B到地面的垂直距离BC.
图28-2-9
