人教版七年级数学上册:4.3.2 角度的计算习题练习(word版,附答案)
文档属性
| 名称 | 人教版七年级数学上册:4.3.2 角度的计算习题练习(word版,附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 63.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览



文档简介
七年级上册数学角度的计算习题
一、选择题
1.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A.
65°
B.
50°
C.
40°
D.
25°
2.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
A.
1个
B.
2个
C.
3个
D.
4个
3.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.
90°
B.
120°
C.
160°
D.
180°
4.一个钝角与一个锐角的差是( )
A.
锐角
B.
钝角
C.
直角
D.
不能确定
5.如图,∠AOB是直角,∠COD也是直角,若∠AOC=,
则∠BOD等于
(
).
A.90°+ B.90°-
C.180°+
D.180°-
6.如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )
A.
如果∠AOB=∠COD,那么∠AOC=∠BOD
B.
如果∠AOB>∠COD,那么∠AOC>∠BOD
C.
如果∠AOB<∠COD,那么∠AOC<∠BOD
D.
如果∠AOB=∠BOC,那么∠AOC=∠BOD
二、填空题
7.比较两角大小的方法有:(1)
法;(2)
法.
三、解答题
8.如图,将一副三角尺的两个直角顶点O重合在一起,在同一平面内旋转其中一个三角尺.
(1)如图1,若∠BOC=70°,求∠AOD的度数.
(2)如图2,若∠BOC=50°,求∠AOD的度数.
(3)如图1,请猜想∠BOC与∠AOD的关系,并写出理由.
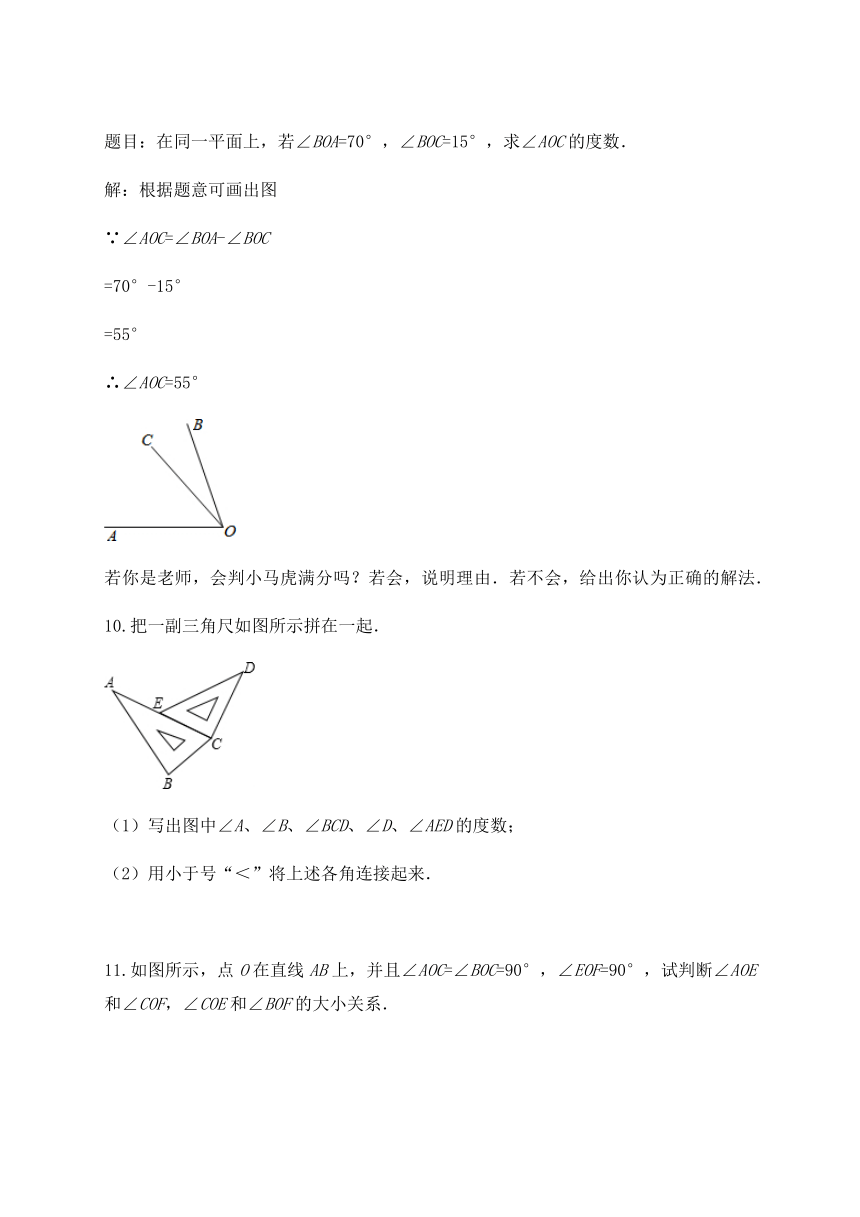
9.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,给出你认为正确的解法.
10.把一副三角尺如图所示拼在一起.
(1)写出图中∠A、∠B、∠BCD、∠D、∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
11.如图所示,点O在直线AB上,并且∠AOC=∠BOC=90°,∠EOF=90°,试判断∠AOE和∠COF,∠COE和∠BOF的大小关系.
12.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.
答案解析
1.【答案】A
【解析】∵∠AOB是一直角,∠AOC=40°,
∴∠COB=50°,
∵OD平分∠BOC,
∴∠COD=25°,
∵∠AOD=∠AOC+∠COD,
∴∠AOD=65°.
故选A.
2.【答案】C
【解析】15°=45°-30°,
65°不能画出,
75°=30°+45°,
135°=45°+90°,
所以能用一副三角尺画出来的有15°、75°,135°共3个,
故选C.
3.【答案】D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°-a,
所以∠AOC+∠BOD=90°+a+90°-a=180°.
故选D.
4.【答案】D
【解析】一个钝角与一个锐角的差可能是锐角、直角也可能是钝角.
故选D.
5.【答案】B
6.【答案】D
【解析】A、如果∠AOB=∠COD,那么∠AOC=∠BOD,本选项正确;
B、如果∠AOB>∠COD,那么∠AOC>∠BOD,本选项正确;
C、如果∠AOB<∠COD,那么∠AOC<∠BOC,本选项正确;
D、如果∠AOB=∠BOC,那么∠AOC=∠BOD,本选项错误.
故选D.
7.【答案】(1)度量;(2)叠合
【解析】角的大小比较的两种方法:(1)度量法,即用量角器量角的度数,角的度数越大,角越大.(2)叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,另一边都不落在重合边的同侧,观察另一边的位置,据此判断即可.
8.【答案】解:(1)∵∠BOC+∠BOD=90,∠BOC=70°,
∴∠BOD=20°,
∴∠AOD=∠AOB+∠BOD=110°.
(2)∵∠AOB=∠DOC=90°,又∵∠AOB+∠AOD+∠DOC+∠BOC=360°,
∴∠BOC+∠AOD=180°
∵∠BOC=50°,
∴∠AOD=180-∠BOC=130°.
(3)结论:∠BOC+∠AOD=180°.
理由:
∵∠AOB=90°,∠COD=90°,
∴∠BOC+∠AOD=(90°-∠AOC)+(90°+∠AOC)=90°-∠AOC+90°+∠AOC=180°,
∴∠BOC+∠AOD=180°.
【解析】(1)∠BOC和∠BOD互余,故∠BOD=20°,故可知∠AOD的度数.
(2)利用∠BOC与∠AOD互补求∠AOD度数.
(3)根据角的互补,叠和部分恰好为∠AOD的补角,故∠BOC和∠AOD的和始终等于180度.
9.【答案】解:不会,如图,当OC在∠AOB的内部时,∠AOC=∠BOA-∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
【解析】在同一平面内,∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
10.【答案】解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
【解析】(1)一副三角尺一个是等腰直角三角形,另一个是一个角为30°的直角三角形,看图写出各个角的度数,(2)按角的大小顺序连接.
11.【答案】解:因为∠EOF=∠COF+∠COE=90°,
∠AOC=∠AOE+∠COE=90°,
即∠AOE和∠COF都与∠COE互余,
根据同角的余角相等得:∠AOE=∠COF,
同理可得出:∠COE=∠BOF.
【解析】根据已知得出∠AOE和∠COF都与∠COE互余,
进而得出∠AOE=∠COF,即可得出:∠COE=∠BOF.
12.【答案】解:∵∠AOC=75°,∠BOC=30°,
∴∠AOB=∠AOC-∠BOC=75°-30°=45°,
又∵∠BOD=75°,
∴∠AOD=∠AOB+∠BOD=45°+75°=120°.
故答案为120°.
【解析】根据∠AOC=∠BOD=75°,∠BOC=30°,利用角的和差关系先求出∠AOB的度数,再求∠AOD.
一、选择题
1.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于( )
A.
65°
B.
50°
C.
40°
D.
25°
2.在15°、65°、75°、135°的角中,能用一副三角尺画出来的有( )
A.
1个
B.
2个
C.
3个
D.
4个
3.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.
90°
B.
120°
C.
160°
D.
180°
4.一个钝角与一个锐角的差是( )
A.
锐角
B.
钝角
C.
直角
D.
不能确定
5.如图,∠AOB是直角,∠COD也是直角,若∠AOC=,
则∠BOD等于
(
).
A.90°+ B.90°-
C.180°+
D.180°-
6.如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )
A.
如果∠AOB=∠COD,那么∠AOC=∠BOD
B.
如果∠AOB>∠COD,那么∠AOC>∠BOD
C.
如果∠AOB<∠COD,那么∠AOC<∠BOD
D.
如果∠AOB=∠BOC,那么∠AOC=∠BOD
二、填空题
7.比较两角大小的方法有:(1)
法;(2)
法.
三、解答题
8.如图,将一副三角尺的两个直角顶点O重合在一起,在同一平面内旋转其中一个三角尺.
(1)如图1,若∠BOC=70°,求∠AOD的度数.
(2)如图2,若∠BOC=50°,求∠AOD的度数.
(3)如图1,请猜想∠BOC与∠AOD的关系,并写出理由.
9.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,给出你认为正确的解法.
10.把一副三角尺如图所示拼在一起.
(1)写出图中∠A、∠B、∠BCD、∠D、∠AED的度数;
(2)用小于号“<”将上述各角连接起来.
11.如图所示,点O在直线AB上,并且∠AOC=∠BOC=90°,∠EOF=90°,试判断∠AOE和∠COF,∠COE和∠BOF的大小关系.
12.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.
答案解析
1.【答案】A
【解析】∵∠AOB是一直角,∠AOC=40°,
∴∠COB=50°,
∵OD平分∠BOC,
∴∠COD=25°,
∵∠AOD=∠AOC+∠COD,
∴∠AOD=65°.
故选A.
2.【答案】C
【解析】15°=45°-30°,
65°不能画出,
75°=30°+45°,
135°=45°+90°,
所以能用一副三角尺画出来的有15°、75°,135°共3个,
故选C.
3.【答案】D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°-a,
所以∠AOC+∠BOD=90°+a+90°-a=180°.
故选D.
4.【答案】D
【解析】一个钝角与一个锐角的差可能是锐角、直角也可能是钝角.
故选D.
5.【答案】B
6.【答案】D
【解析】A、如果∠AOB=∠COD,那么∠AOC=∠BOD,本选项正确;
B、如果∠AOB>∠COD,那么∠AOC>∠BOD,本选项正确;
C、如果∠AOB<∠COD,那么∠AOC<∠BOC,本选项正确;
D、如果∠AOB=∠BOC,那么∠AOC=∠BOD,本选项错误.
故选D.
7.【答案】(1)度量;(2)叠合
【解析】角的大小比较的两种方法:(1)度量法,即用量角器量角的度数,角的度数越大,角越大.(2)叠合法,即将两个角叠合在一起比较,使两个角的顶点及一边重合,另一边都不落在重合边的同侧,观察另一边的位置,据此判断即可.
8.【答案】解:(1)∵∠BOC+∠BOD=90,∠BOC=70°,
∴∠BOD=20°,
∴∠AOD=∠AOB+∠BOD=110°.
(2)∵∠AOB=∠DOC=90°,又∵∠AOB+∠AOD+∠DOC+∠BOC=360°,
∴∠BOC+∠AOD=180°
∵∠BOC=50°,
∴∠AOD=180-∠BOC=130°.
(3)结论:∠BOC+∠AOD=180°.
理由:
∵∠AOB=90°,∠COD=90°,
∴∠BOC+∠AOD=(90°-∠AOC)+(90°+∠AOC)=90°-∠AOC+90°+∠AOC=180°,
∴∠BOC+∠AOD=180°.
【解析】(1)∠BOC和∠BOD互余,故∠BOD=20°,故可知∠AOD的度数.
(2)利用∠BOC与∠AOD互补求∠AOD度数.
(3)根据角的互补,叠和部分恰好为∠AOD的补角,故∠BOC和∠AOD的和始终等于180度.
9.【答案】解:不会,如图,当OC在∠AOB的内部时,∠AOC=∠BOA-∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
【解析】在同一平面内,∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
10.【答案】解:(1)∠A=30°,∠B=90°,∠BCD=150°,∠D=45°,∠AED=135°;
(2)∠A<∠D<∠B<∠AED<∠BCD.
【解析】(1)一副三角尺一个是等腰直角三角形,另一个是一个角为30°的直角三角形,看图写出各个角的度数,(2)按角的大小顺序连接.
11.【答案】解:因为∠EOF=∠COF+∠COE=90°,
∠AOC=∠AOE+∠COE=90°,
即∠AOE和∠COF都与∠COE互余,
根据同角的余角相等得:∠AOE=∠COF,
同理可得出:∠COE=∠BOF.
【解析】根据已知得出∠AOE和∠COF都与∠COE互余,
进而得出∠AOE=∠COF,即可得出:∠COE=∠BOF.
12.【答案】解:∵∠AOC=75°,∠BOC=30°,
∴∠AOB=∠AOC-∠BOC=75°-30°=45°,
又∵∠BOD=75°,
∴∠AOD=∠AOB+∠BOD=45°+75°=120°.
故答案为120°.
【解析】根据∠AOC=∠BOD=75°,∠BOC=30°,利用角的和差关系先求出∠AOB的度数,再求∠AOD.
