北师大版九年级数学上册 第三章 概率的进一步认识 单元检测试题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册 第三章 概率的进一步认识 单元检测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 09:58:30 | ||
图片预览




文档简介
1132840011328400123190000第三章 概率的进一步认识 单元检测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 从一批电视机中随机抽取10台进行质检,其中一台是次品,下列说法正确的是( )
A.次品率小于10% B.次品率大于10%
C.次品率接近10% D.次品率等于10%
?2. 在一个不透明的布袋中装有红色,白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( )
A.4个 B.6个 C.34个 D.36个
?
3. 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是(? ? ? ? )
A.12 B.14 C.13 D.34
?
4. 小郭、小王两人打算搭乘同一班次电车上学,若此班次电车共有5节车厢,且小郭从任意一节车厢上车的机会相等,小王从任意一节车厢上车的机会相等,则两人从同一节车厢上车的概率为(? ? ? ? ?)
A.12 B.15 C.110 D.125
?
5. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )
A.12个 B.16个 C.20个 D.25个
?
6. 某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是(? ? ? ? )
A.12 B.14 C.16 D.116
?
7. 在一个不透明的袋子中装有2个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该实验多次,发现摸到白球的频率稳定在0.4,由此可判断袋子中黑球的个数为( )
A.2个 B.3个 C.4个 D.5个
?
8. 一个不透明的袋子中放有2个红球,2个白球(红球和白球的形状、材质完全相同),从中任意摸出2个球,恰好是一个红球、一个白球的概率是( )
A.14 B.12 C.13 D.23
?
9. 学校要从茗茗、墨墨和丽丽三人中随机选两人去参加演讲比赛,则茗茗和丽丽同时入选的概率是( )
A.16 B.13 C.23 D.12
?
10. 在不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其它差别.每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,则袋中白球有( )
A.12个 B.20个 C.24个 D.40个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 往一个装了很多白球的袋子里放入10个黑球,每次倒出5个,记下所倒出的黑球的数目,再把它们放回去,共倒了120次,倒出黑球240个,袋子里原有白球约________?个.
?
12. 在一个不透明的箱子中装有4件同型号的产品,其中合格品3件、不合格品1件,现在从这4件产品中随机抽取2件检测,则抽到的都是合格品的概率是________.
?
13. 在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,一人从中随机摸出一球记下标号后放回,再从中随机摸出一个小球记下标号,则两次摸出的小球的标号之和大于4的概率是________.
?
14. 同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为________.
?
15. 甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.若从甲、乙两所医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是________.
?
16. 频率估计概率:在一黑色不透明的袋子里装有大小颜色相同的小球若干,在袋中随机摸出5个小球做上记号后放回袋子中,摇匀后再随机摸出5个球,其中有1个是带记号的小球,则可以估计这个袋子中一共大约有________个球.
?
17. 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是________.
?
18. 有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为________.
?
19. 一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜色外完全相同,随机摸出两个小球,则摸出两个颜色不同小球的概率是________.
?
20. 一个口袋中有三个完全相同的小球,把它们分别标号为123,随机地摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的小球标号的和等于4的概率是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 泰州具有丰富的旅游资源,小明利用周日来泰州游玩,上午从A、B两个景点中任意选择一个游玩,下午从C、D、E三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有等可能的结果,并求小明恰好选中景点B和C的概率.
?
22. 本校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:
(1)甲、乙两名学生在同一餐厅用餐的概率;
(2)甲、乙两名学生至少有一人在B餐厅的概率.
?
23. 检查某工厂产品,其结果如下:检查产品件数分别为:10,20,50,100,200,400,800,1600.其中次品数分别为:0,3,6,9,18,41,79,160.问:
(1)次品的频率分别是多少?
(2)估计该工厂产品出现次品的概率是多少?
?
24. 一只不透明的袋子,装有分别标有数字1、2、3的三个球,这些球除所标的数字外都相同,搅匀后从中摸出1个球,记录下数字后放回袋中并搅匀,再从中任意摸出1个球,记录下数字,请用列表或画树状图的方法,求出两次摸出的球上的数字之和为偶数的概率.
?
25. 小明和小亮计划暑期结伴参加志愿者活动,小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动,他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4,5,6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动,你认为这个游戏公平吗?请说明理由.
?
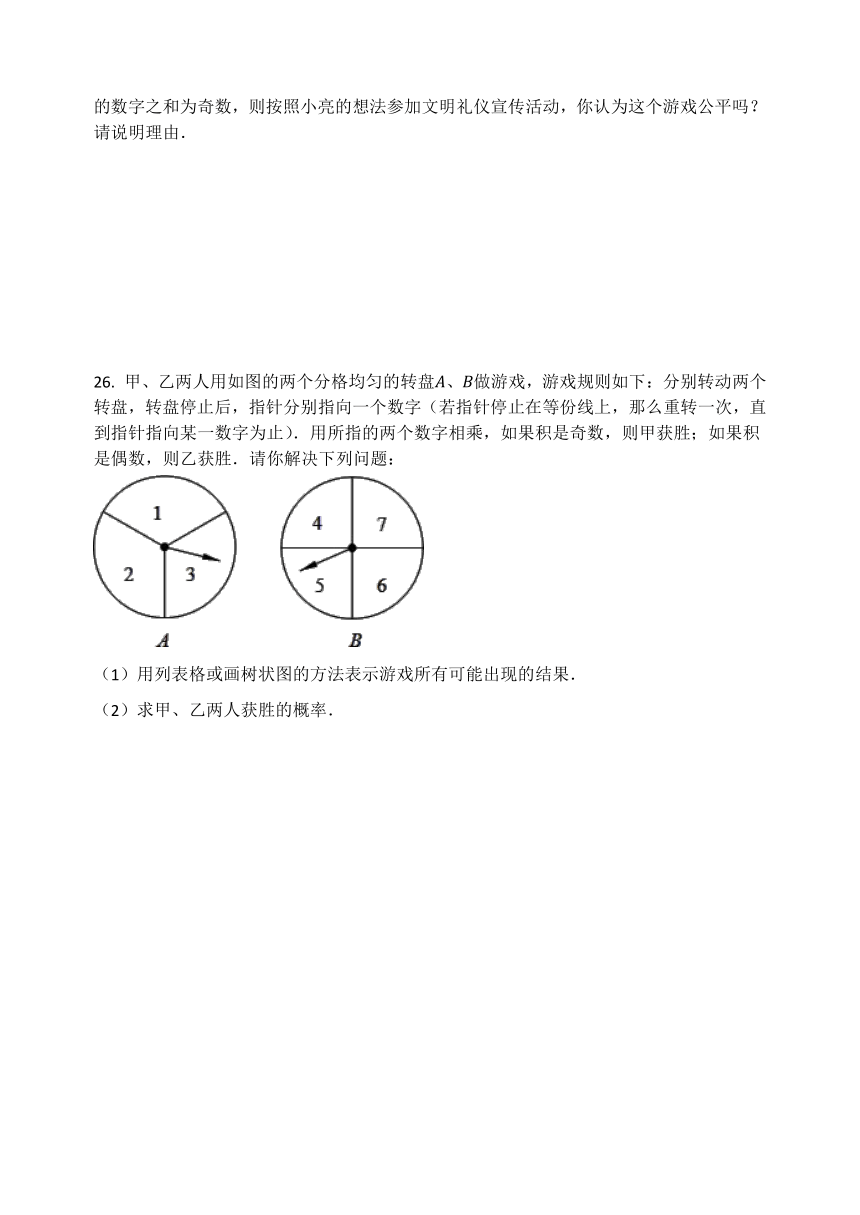
26. 甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:由题意知,抽取10台,出现1台是次品,只能说次品率接近10%,故选C.
2.
【答案】
B
【解答】
∵ 摸到红色球的频率稳定在15%左右,
∴ 口袋中红色球的频率为15%,故红球的个数为40×15%=6个.
3.
【答案】
A
【解答】
解:画树状图为:
共有6种等可能的结果数,其中一个为红色,另一个转出蓝色的占3种,
则可配成紫色的概率=36=12.
故选A.
4.
【答案】
B
【解答】
解:记5节车厢分别为A,B,C,D,E,由题意列表如下:
小郭
小王
A
B
C
D
E
A
(A,A)
(A,B)
(A,C)
(A,D)
(A,E)
B
(B,A)
(B,B)
(B,C)
(B,D)
(B,E)
C
(C,A)
(C,B)
(C,C)
(C,D)
(C,E)
D
(D,A)
(D,B)
(D,C)
(D,D)
(D,E)
E
(E,A)
(E,B)
(E,C)
(E,D)
(E,E)
由上表可知,共有25种等可能的结果,其中两人从同一节车厢上车的结果有5种,故所求概率为525=15.
故选B.
5.
【答案】
B
【解答】
设盒子中有红球x个,由题意可得:4x+4=0.2,
解得:x=16,
6.
【答案】
B
【解答】
解:画树状图如下:
由树状图可知,共有16种等可能结果,其中佳佳和琪琪恰好从同一个入口进入该公园的有4种等可能结果,
所以佳佳和琪琪恰好从同一个入口进入该公园的概率为416=14.
故选B.
7.
【答案】
B
【解答】
解:设袋中黑色球可能有x个.
根据题意,任意摸出1个,摸到白球的概率是:0.4=22+x,
解得:x=3.
故选B.
8.
【答案】
D
【解答】
列树形图得:
∵ 共12种情况,其中一红一白的有8种情况,
∴ 恰好是一个红球、一个白球的概率是812=23,
9.
【答案】
B
【解答】
解:列表如下:
共有3种等可能的结果数,其中茗茗和丽丽同时入选的结果数占1种,
所以茗茗和丽丽同时入选的概率=13.
故选B.
10.
【答案】
C
【解答】
设袋中白球有x个,根据题意得:
x16+x=0.6,
解得:x=24,
经检验:x=24是分式方程的解,
故袋中白球有24个.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
15
【解答】
解:根据题意,得
黑球的概率是240600=25,
则袋子里球的个数共是10÷25=25(个),25-10=15(个).
则袋子里原有白球15个,
故答案为15.
12.
【答案】
12
【解答】
画树状图得:
∵ 共有12种等可能的结果,抽到的都是合格品的有6种情况,
∴ 抽到的都是合格品的概率是:612=12.
13.
【答案】
58
【解答】
解:画树状图得:
∵ 共有16种等可能的结果,两次摸出的小球的标号之和大于4的有10种情况,
∴ 两次摸出的小球的标号之和大于4的概率是:1016=58.
14.
【答案】
16
【解答】
列表得:
(1,?6)
(2,?6)
(3,?6)
(4,?6)
(5,?6)
(6,?6)
(1,?5)
(2,?5)
(3,?5)
(4,?5)
(5,?5)
(6,?5)
(1,?4)
(2,?4)
(3,?4)
(4,?4)
(5,?4)
(6,?4)
(1,?3)
(2,?3)
(3,?3)
(4,?3)
(5,?3)
(6,?3)
(1,?2)
(2,?2)
(3,?2)
(4,?2)
(5,?2)
(6,?2)
(1,?1)
(2,?1)
(3,?1)
(4,?1)
(5,?1)
(6,?1)
由表可知一共有36种情况,两枚骰子点数相同的有6种,
所以两枚骰子点数相同的概率为636=16,
15.
【答案】
12
【解答】
解:根据题意列表如下:
? ? ?男
? ? 女
? ?男
? (男,男)
? (男,女)
? ?女
? (男,女)
? (女,女)
由上表可知,共有4种可能的情况数,其中所选的2名医护人员性别相同的情况有2种,
则所选的2名医护人员性别相同的概率是24=12.
故答案为:12.
16.
【答案】
25
【解答】
解:设这个袋子中共有x个小球,
根据题意得5x=15,
解得x=25,
所以可以估计这个袋子中一共大约有25个球.
故答案为25.
17.
【答案】
13
【解答】
列表得:
红1
红2
白1
白2
红1
---
(红2,红1)
(白1,红1)
(白2,红1)
红2
(红1,红2)
---
(白1,红2)
(白2,红2)
白1
(红1,白1)
(红2,白1)
---
(白2,白1)
白2
(红1,白2)
(红2,白2)
(白1,白2)
---
所有等可能的情况有12种,其中第一个人摸到红球且第二个人摸到白球的情况有4种,
则P=412=13.
18.
【答案】
600个
【解答】
解:∵ 摸到红球的频率约为0.6,
∴ 红球所占的百分比是60%.
∴ 1000×60%=600(个).
故答案为:600个.
19.
【答案】
35
【解答】
画树状图如下:
由树状图可知,共有20种等可能结果,其中取出的小球颜色不同的有12种结果,
∴ 两次取出的小球颜色不同的概率为1220=35,
20.
【答案】
13
【解答】
根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和为4的有3种,
∴ 两次摸出的小球标号的和等于4的概率是39=13,
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:列表如下:
A
B
C
AC
BC
D
AD
BD
E
AE
BE
由表可知共有6种等可能的结果数,其中小明恰好选中景点B和C的结果有1种,
所以小明恰好选中景点B和C的概率为16.
【解答】
解:列表如下:
A
B
C
AC
BC
D
AD
BD
E
AE
BE
由表可知共有6种等可能的结果数,其中小明恰好选中景点B和C的结果有1种,
所以小明恰好选中景点B和C的概率为16.
22.
【答案】
解:(1)画树形图得:
∵ 甲、乙两名学生在餐厅用餐的情况有AB、AA、BA、BB,
∴ P(甲、乙两名学生在同一餐厅用餐)=24=12;
(2)由(1)的树形图可知P(甲、乙两名学生至少有一人在B餐厅)=34.
【解答】
解:(1)画树形图得:
∵ 甲、乙两名学生在餐厅用餐的情况有AB、AA、BA、BB,
∴ P(甲、乙两名学生在同一餐厅用餐)=24=12;
(2)由(1)的树形图可知P(甲、乙两名学生至少有一人在B餐厅)=34.
23.
【答案】
解:(1)∵ 检查产品件数分别为:10,20,50,100,200,400,800,1600,其中次品数分别为:0,3,6,9,18,41,79,160,
∴ 次品的频率分别是:0÷10=0,3÷20=0.15,6÷50=0.12,9÷100=0.09,18÷200=0.09,41÷400=0.1025,79÷800=0.09875,160÷1600=0.1;
(2)从(1)中所求的数据可看到,当抽取件数(即重复试验次数)n越大,“出现次品”事件发生的频率mn就越接近常数0.1,
所以“出现次品”的概率约为0.1.
【解答】
解:(1)∵ 检查产品件数分别为:10,20,50,100,200,400,800,1600,其中次品数分别为:0,3,6,9,18,41,79,160,
∴ 次品的频率分别是:0÷10=0,3÷20=0.15,6÷50=0.12,9÷100=0.09,18÷200=0.09,41÷400=0.1025,79÷800=0.09875,160÷1600=0.1;
(2)从(1)中所求的数据可看到,当抽取件数(即重复试验次数)n越大,“出现次品”事件发生的频率mn就越接近常数0.1,
所以“出现次品”的概率约为0.1.
24.
【答案】
画树状图得:
∵ 共有9种等可能的结果,两次摸出的球上的数字之和为偶数的有5种情况,
∴ 两次摸出的球上的数字之和为偶数的概率为:59.
【解答】
画树状图得:
∵ 共有9种等可能的结果,两次摸出的球上的数字之和为偶数的有5种情况,
∴ 两次摸出的球上的数字之和为偶数的概率为:59.
25.
【答案】
解:游戏不公平,
理由:列表如下:
小明\小亮
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表格可知,共有9种等可能的情况,其中数字之和为偶数的情况有5种,奇数有4种,
∴ P(小明获胜)=59,P(小亮获胜)=49,
∴ 这个游戏不公平.
【解答】
解:游戏不公平,
理由:列表如下:
小明\小亮
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表格可知,共有9种等可能的情况,其中数字之和为偶数的情况有5种,奇数有4种,
∴ P(小明获胜)=59,P(小亮获胜)=49,
∴ 这个游戏不公平.
26.
【答案】
所有可能出现的结果如图:
4
5
6
7
1
(1,?4)
(1,?5)
(1,?6)
(1,?7)
2
(2,?4)
(2,?5)
(2,?6)
(2,?7)
3
(3,?4)
(3,?5)
(3,?6)
(3,?7)
从上面的表格(或树状图)可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中积是奇数的结果有4种,即5、7、15、21,积是偶数的结果有8种,即4、6、8、10、12、14、12、18,
∴ 甲、乙?两人获胜的概率分别为:
P(甲获胜)=412=13,
P(乙获胜)=812=23.
【解答】
所有可能出现的结果如图:
4
5
6
7
1
(1,?4)
(1,?5)
(1,?6)
(1,?7)
2
(2,?4)
(2,?5)
(2,?6)
(2,?7)
3
(3,?4)
(3,?5)
(3,?6)
(3,?7)
从上面的表格(或树状图)可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中积是奇数的结果有4种,即5、7、15、21,积是偶数的结果有8种,即4、6、8、10、12、14、12、18,
∴ 甲、乙?两人获胜的概率分别为:
P(甲获胜)=412=13,
P(乙获胜)=812=23.
.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 从一批电视机中随机抽取10台进行质检,其中一台是次品,下列说法正确的是( )
A.次品率小于10% B.次品率大于10%
C.次品率接近10% D.次品率等于10%
?2. 在一个不透明的布袋中装有红色,白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( )
A.4个 B.6个 C.34个 D.36个
?
3. 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是(? ? ? ? )
A.12 B.14 C.13 D.34
?
4. 小郭、小王两人打算搭乘同一班次电车上学,若此班次电车共有5节车厢,且小郭从任意一节车厢上车的机会相等,小王从任意一节车厢上车的机会相等,则两人从同一节车厢上车的概率为(? ? ? ? ?)
A.12 B.15 C.110 D.125
?
5. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )
A.12个 B.16个 C.20个 D.25个
?
6. 某市公园的东、南、西、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是(? ? ? ? )
A.12 B.14 C.16 D.116
?
7. 在一个不透明的袋子中装有2个白球和若干个黑球,它们除颜色外完全相同,从袋子中随机摸出一球,记下颜色并放回,重复该实验多次,发现摸到白球的频率稳定在0.4,由此可判断袋子中黑球的个数为( )
A.2个 B.3个 C.4个 D.5个
?
8. 一个不透明的袋子中放有2个红球,2个白球(红球和白球的形状、材质完全相同),从中任意摸出2个球,恰好是一个红球、一个白球的概率是( )
A.14 B.12 C.13 D.23
?
9. 学校要从茗茗、墨墨和丽丽三人中随机选两人去参加演讲比赛,则茗茗和丽丽同时入选的概率是( )
A.16 B.13 C.23 D.12
?
10. 在不透明的袋子里装有16个红球和若干个白球,这些球除颜色不同外无其它差别.每次从袋子里摸出一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,则袋中白球有( )
A.12个 B.20个 C.24个 D.40个
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 往一个装了很多白球的袋子里放入10个黑球,每次倒出5个,记下所倒出的黑球的数目,再把它们放回去,共倒了120次,倒出黑球240个,袋子里原有白球约________?个.
?
12. 在一个不透明的箱子中装有4件同型号的产品,其中合格品3件、不合格品1件,现在从这4件产品中随机抽取2件检测,则抽到的都是合格品的概率是________.
?
13. 在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,一人从中随机摸出一球记下标号后放回,再从中随机摸出一个小球记下标号,则两次摸出的小球的标号之和大于4的概率是________.
?
14. 同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为________.
?
15. 甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.若从甲、乙两所医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是________.
?
16. 频率估计概率:在一黑色不透明的袋子里装有大小颜色相同的小球若干,在袋中随机摸出5个小球做上记号后放回袋子中,摇匀后再随机摸出5个球,其中有1个是带记号的小球,则可以估计这个袋子中一共大约有________个球.
?
17. 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是________.
?
18. 有一箱规格相同的红、黄两种颜色的小塑料球共1000个.为了估计这两种颜色的球各有多少个,小明将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后.发现摸到红球的频率约为0.6,据此可以估计红球的个数约为________.
?
19. 一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜色外完全相同,随机摸出两个小球,则摸出两个颜色不同小球的概率是________.
?
20. 一个口袋中有三个完全相同的小球,把它们分别标号为123,随机地摸出一个小球,然后放回,再随机摸出一个小球,则两次摸出的小球标号的和等于4的概率是________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 泰州具有丰富的旅游资源,小明利用周日来泰州游玩,上午从A、B两个景点中任意选择一个游玩,下午从C、D、E三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有等可能的结果,并求小明恰好选中景点B和C的概率.
?
22. 本校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:
(1)甲、乙两名学生在同一餐厅用餐的概率;
(2)甲、乙两名学生至少有一人在B餐厅的概率.
?
23. 检查某工厂产品,其结果如下:检查产品件数分别为:10,20,50,100,200,400,800,1600.其中次品数分别为:0,3,6,9,18,41,79,160.问:
(1)次品的频率分别是多少?
(2)估计该工厂产品出现次品的概率是多少?
?
24. 一只不透明的袋子,装有分别标有数字1、2、3的三个球,这些球除所标的数字外都相同,搅匀后从中摸出1个球,记录下数字后放回袋中并搅匀,再从中任意摸出1个球,记录下数字,请用列表或画树状图的方法,求出两次摸出的球上的数字之和为偶数的概率.
?
25. 小明和小亮计划暑期结伴参加志愿者活动,小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动,他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4,5,6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动,你认为这个游戏公平吗?请说明理由.
?
26. 甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:由题意知,抽取10台,出现1台是次品,只能说次品率接近10%,故选C.
2.
【答案】
B
【解答】
∵ 摸到红色球的频率稳定在15%左右,
∴ 口袋中红色球的频率为15%,故红球的个数为40×15%=6个.
3.
【答案】
A
【解答】
解:画树状图为:
共有6种等可能的结果数,其中一个为红色,另一个转出蓝色的占3种,
则可配成紫色的概率=36=12.
故选A.
4.
【答案】
B
【解答】
解:记5节车厢分别为A,B,C,D,E,由题意列表如下:
小郭
小王
A
B
C
D
E
A
(A,A)
(A,B)
(A,C)
(A,D)
(A,E)
B
(B,A)
(B,B)
(B,C)
(B,D)
(B,E)
C
(C,A)
(C,B)
(C,C)
(C,D)
(C,E)
D
(D,A)
(D,B)
(D,C)
(D,D)
(D,E)
E
(E,A)
(E,B)
(E,C)
(E,D)
(E,E)
由上表可知,共有25种等可能的结果,其中两人从同一节车厢上车的结果有5种,故所求概率为525=15.
故选B.
5.
【答案】
B
【解答】
设盒子中有红球x个,由题意可得:4x+4=0.2,
解得:x=16,
6.
【答案】
B
【解答】
解:画树状图如下:
由树状图可知,共有16种等可能结果,其中佳佳和琪琪恰好从同一个入口进入该公园的有4种等可能结果,
所以佳佳和琪琪恰好从同一个入口进入该公园的概率为416=14.
故选B.
7.
【答案】
B
【解答】
解:设袋中黑色球可能有x个.
根据题意,任意摸出1个,摸到白球的概率是:0.4=22+x,
解得:x=3.
故选B.
8.
【答案】
D
【解答】
列树形图得:
∵ 共12种情况,其中一红一白的有8种情况,
∴ 恰好是一个红球、一个白球的概率是812=23,
9.
【答案】
B
【解答】
解:列表如下:
共有3种等可能的结果数,其中茗茗和丽丽同时入选的结果数占1种,
所以茗茗和丽丽同时入选的概率=13.
故选B.
10.
【答案】
C
【解答】
设袋中白球有x个,根据题意得:
x16+x=0.6,
解得:x=24,
经检验:x=24是分式方程的解,
故袋中白球有24个.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
15
【解答】
解:根据题意,得
黑球的概率是240600=25,
则袋子里球的个数共是10÷25=25(个),25-10=15(个).
则袋子里原有白球15个,
故答案为15.
12.
【答案】
12
【解答】
画树状图得:
∵ 共有12种等可能的结果,抽到的都是合格品的有6种情况,
∴ 抽到的都是合格品的概率是:612=12.
13.
【答案】
58
【解答】
解:画树状图得:
∵ 共有16种等可能的结果,两次摸出的小球的标号之和大于4的有10种情况,
∴ 两次摸出的小球的标号之和大于4的概率是:1016=58.
14.
【答案】
16
【解答】
列表得:
(1,?6)
(2,?6)
(3,?6)
(4,?6)
(5,?6)
(6,?6)
(1,?5)
(2,?5)
(3,?5)
(4,?5)
(5,?5)
(6,?5)
(1,?4)
(2,?4)
(3,?4)
(4,?4)
(5,?4)
(6,?4)
(1,?3)
(2,?3)
(3,?3)
(4,?3)
(5,?3)
(6,?3)
(1,?2)
(2,?2)
(3,?2)
(4,?2)
(5,?2)
(6,?2)
(1,?1)
(2,?1)
(3,?1)
(4,?1)
(5,?1)
(6,?1)
由表可知一共有36种情况,两枚骰子点数相同的有6种,
所以两枚骰子点数相同的概率为636=16,
15.
【答案】
12
【解答】
解:根据题意列表如下:
? ? ?男
? ? 女
? ?男
? (男,男)
? (男,女)
? ?女
? (男,女)
? (女,女)
由上表可知,共有4种可能的情况数,其中所选的2名医护人员性别相同的情况有2种,
则所选的2名医护人员性别相同的概率是24=12.
故答案为:12.
16.
【答案】
25
【解答】
解:设这个袋子中共有x个小球,
根据题意得5x=15,
解得x=25,
所以可以估计这个袋子中一共大约有25个球.
故答案为25.
17.
【答案】
13
【解答】
列表得:
红1
红2
白1
白2
红1
---
(红2,红1)
(白1,红1)
(白2,红1)
红2
(红1,红2)
---
(白1,红2)
(白2,红2)
白1
(红1,白1)
(红2,白1)
---
(白2,白1)
白2
(红1,白2)
(红2,白2)
(白1,白2)
---
所有等可能的情况有12种,其中第一个人摸到红球且第二个人摸到白球的情况有4种,
则P=412=13.
18.
【答案】
600个
【解答】
解:∵ 摸到红球的频率约为0.6,
∴ 红球所占的百分比是60%.
∴ 1000×60%=600(个).
故答案为:600个.
19.
【答案】
35
【解答】
画树状图如下:
由树状图可知,共有20种等可能结果,其中取出的小球颜色不同的有12种结果,
∴ 两次取出的小球颜色不同的概率为1220=35,
20.
【答案】
13
【解答】
根据题意,画树状图如下:
共有9种等可能结果,其中两次摸出的小球标号的和为4的有3种,
∴ 两次摸出的小球标号的和等于4的概率是39=13,
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:列表如下:
A
B
C
AC
BC
D
AD
BD
E
AE
BE
由表可知共有6种等可能的结果数,其中小明恰好选中景点B和C的结果有1种,
所以小明恰好选中景点B和C的概率为16.
【解答】
解:列表如下:
A
B
C
AC
BC
D
AD
BD
E
AE
BE
由表可知共有6种等可能的结果数,其中小明恰好选中景点B和C的结果有1种,
所以小明恰好选中景点B和C的概率为16.
22.
【答案】
解:(1)画树形图得:
∵ 甲、乙两名学生在餐厅用餐的情况有AB、AA、BA、BB,
∴ P(甲、乙两名学生在同一餐厅用餐)=24=12;
(2)由(1)的树形图可知P(甲、乙两名学生至少有一人在B餐厅)=34.
【解答】
解:(1)画树形图得:
∵ 甲、乙两名学生在餐厅用餐的情况有AB、AA、BA、BB,
∴ P(甲、乙两名学生在同一餐厅用餐)=24=12;
(2)由(1)的树形图可知P(甲、乙两名学生至少有一人在B餐厅)=34.
23.
【答案】
解:(1)∵ 检查产品件数分别为:10,20,50,100,200,400,800,1600,其中次品数分别为:0,3,6,9,18,41,79,160,
∴ 次品的频率分别是:0÷10=0,3÷20=0.15,6÷50=0.12,9÷100=0.09,18÷200=0.09,41÷400=0.1025,79÷800=0.09875,160÷1600=0.1;
(2)从(1)中所求的数据可看到,当抽取件数(即重复试验次数)n越大,“出现次品”事件发生的频率mn就越接近常数0.1,
所以“出现次品”的概率约为0.1.
【解答】
解:(1)∵ 检查产品件数分别为:10,20,50,100,200,400,800,1600,其中次品数分别为:0,3,6,9,18,41,79,160,
∴ 次品的频率分别是:0÷10=0,3÷20=0.15,6÷50=0.12,9÷100=0.09,18÷200=0.09,41÷400=0.1025,79÷800=0.09875,160÷1600=0.1;
(2)从(1)中所求的数据可看到,当抽取件数(即重复试验次数)n越大,“出现次品”事件发生的频率mn就越接近常数0.1,
所以“出现次品”的概率约为0.1.
24.
【答案】
画树状图得:
∵ 共有9种等可能的结果,两次摸出的球上的数字之和为偶数的有5种情况,
∴ 两次摸出的球上的数字之和为偶数的概率为:59.
【解答】
画树状图得:
∵ 共有9种等可能的结果,两次摸出的球上的数字之和为偶数的有5种情况,
∴ 两次摸出的球上的数字之和为偶数的概率为:59.
25.
【答案】
解:游戏不公平,
理由:列表如下:
小明\小亮
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表格可知,共有9种等可能的情况,其中数字之和为偶数的情况有5种,奇数有4种,
∴ P(小明获胜)=59,P(小亮获胜)=49,
∴ 这个游戏不公平.
【解答】
解:游戏不公平,
理由:列表如下:
小明\小亮
4
5
6
4
8
9
10
5
9
10
11
6
10
11
12
由表格可知,共有9种等可能的情况,其中数字之和为偶数的情况有5种,奇数有4种,
∴ P(小明获胜)=59,P(小亮获胜)=49,
∴ 这个游戏不公平.
26.
【答案】
所有可能出现的结果如图:
4
5
6
7
1
(1,?4)
(1,?5)
(1,?6)
(1,?7)
2
(2,?4)
(2,?5)
(2,?6)
(2,?7)
3
(3,?4)
(3,?5)
(3,?6)
(3,?7)
从上面的表格(或树状图)可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中积是奇数的结果有4种,即5、7、15、21,积是偶数的结果有8种,即4、6、8、10、12、14、12、18,
∴ 甲、乙?两人获胜的概率分别为:
P(甲获胜)=412=13,
P(乙获胜)=812=23.
【解答】
所有可能出现的结果如图:
4
5
6
7
1
(1,?4)
(1,?5)
(1,?6)
(1,?7)
2
(2,?4)
(2,?5)
(2,?6)
(2,?7)
3
(3,?4)
(3,?5)
(3,?6)
(3,?7)
从上面的表格(或树状图)可以看出,所有可能出现的结果共有12种,且每种结果出现的可能性相同,其中积是奇数的结果有4种,即5、7、15、21,积是偶数的结果有8种,即4、6、8、10、12、14、12、18,
∴ 甲、乙?两人获胜的概率分别为:
P(甲获胜)=412=13,
P(乙获胜)=812=23.
.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
