青岛版数学八年级上5.3根号2是有理数吗?
文档属性
| 名称 | 青岛版数学八年级上5.3根号2是有理数吗? |

|
|
| 格式 | zip | ||
| 文件大小 | 907.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-05 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
第五章:实数
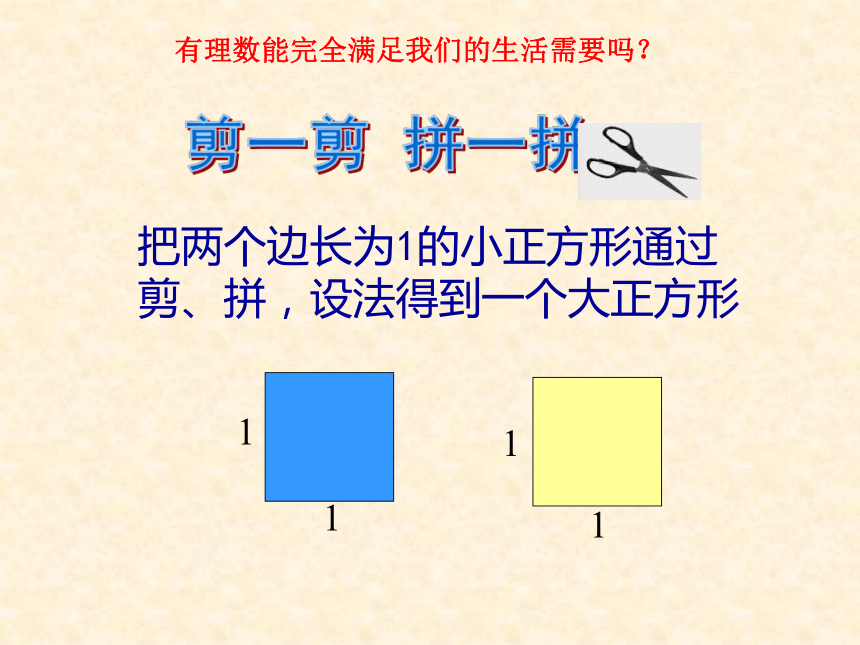
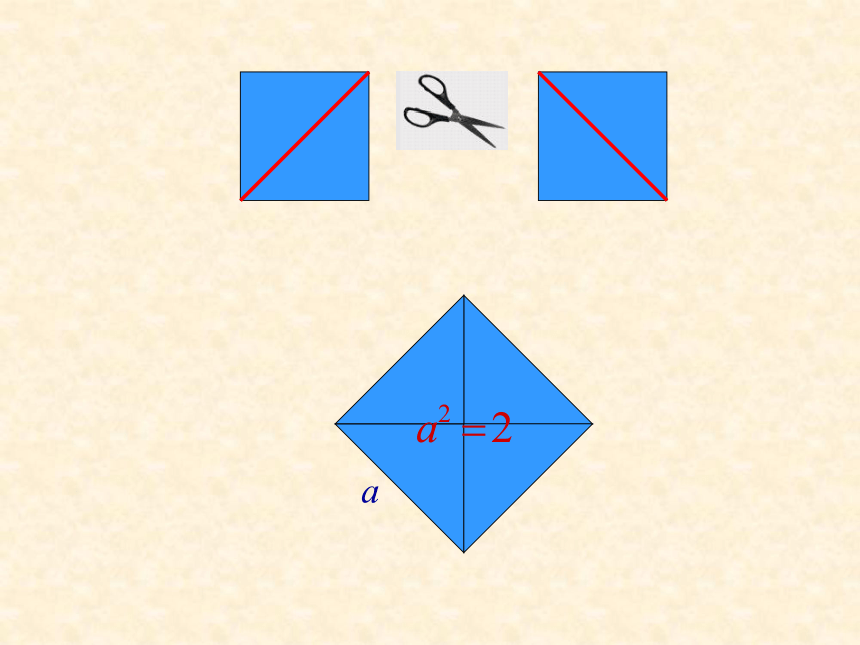
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
1
1
1
1
有理数能完全满足我们的生活需要吗?
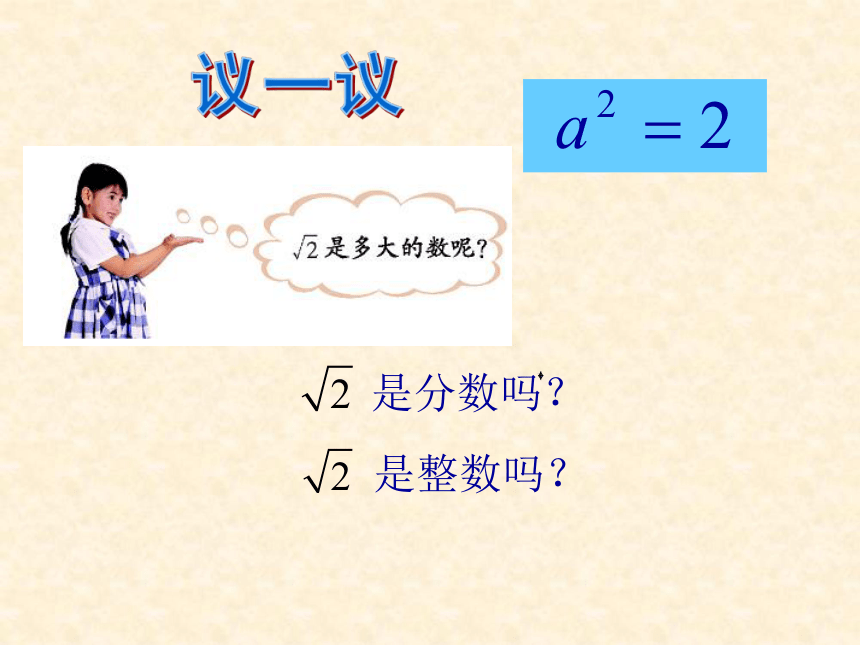
是整数吗?
是分数吗?
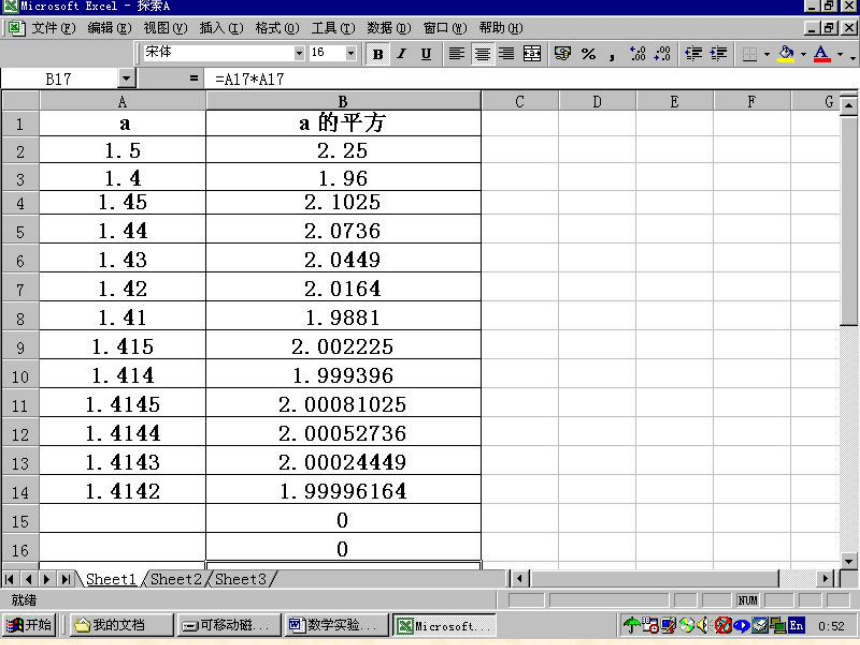
是多少?
它是一个无限不循环小数
=1.41421356…
然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
1
1
1
C
B
A
b
b是有理数吗?
你能设法用多种方法找出几个这样的非有理数吗?请说明理由.
(1)面积为5、8、10等非平方数的正方形的边长;
(2)边长为2的等边三角形的高;
(3)通过构造直角三角形;
(4)列方程.如x =3.等等
议一议
跟踪训练
(1)、在数0, 1, ,0.1235中,无理数的个数为( )
A.0个 B.1个 C.2个 D.3个
(2)、下列各数3.14, ,0, ,3.1414414441…
(相邻两个1之间4的个数逐次加1)中,( )是有理数,( )是无理数。
(3)、边长为2的正方形的对角线是( )
A.整数 B.有理数 C.分数 D.无理数
如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.
试一试
(1)每人至少找出3条长度为非有理数
的线段;
(2)最长的非有理数线段是哪一条?
最短的非有理数线段
是哪一条?为什么?
温馨提示:带根号的数并不都是无理数,反之,无理数也并非都带根号。判断一个数是不是无理数,应从定义出发,看它是不是无限不循环小数。
温馨提示:有理数与无理数的区别:有理数包括整数和分数,而分数都可化成有限小数和无限循环小数的形式;把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数。
2、下列说法:(1)有理数都是有限小数
(2)有限小数都是有理数
(3)无理数都是无限小数
(4)无限小数都是无理数,
其中正确的为______________________________。
3、一个面积为13cm2的正方形,它的边长是________
4、已知正数m满足m2=39,则m的整数部分是_________
给出单位长度为1的线段,你会做出长度为的线段吗?会做出长度分别为 与 的线段吗?
(1)如下图,OA=OB,数轴上A点对应的数是什么?
它介于哪两个整数之间?
(2)如果将所有有理数都标到数轴上,那么数轴被
填满了吗?
-2
-1
0
1
2
B
A
无理数跟有理数一样,也可以用数轴上的点表示,这是对无理数的几何解释。
温馨提示:
并不是所有的无理数都能用尺规作图的方法在数轴上作出它对应的点。
3、在数轴上作出 对应的点。
-2
-1
0
1
2
达标测评:
1、选择题:(1)、做一个边长为13平方厘米的正方形,它的边长是( )
A、一个整数 B、一个分数 C、一个有理数 D、一个无理数
(2)、在实数0,1,0.1235, 中,无理数的个数为( )
A、0个 B、1个 C、2个 D、3个
2、填空题:
(3)、写出一个比 小的整数( )
(4)、无理数可以利用数轴上的点表示,数轴上的点表示的( )是无理数(填“一定”或“不一定”)
课堂小结:
1、体验无理数的几何解释,明白数轴上有些点表示有理数,有些表示无理数,加深对数轴的认识。
2、要综合运用勾股定理和算术平方根、无理数等知识来求两点间距离,注意仔细观察以及数形结合思想的运用。
1
1
毕达哥拉斯树
螺形图
欣赏有趣的图形:
点击
第五章:实数
把两个边长为1的小正方形通过剪、拼,设法得到一个大正方形
1
1
1
1
有理数能完全满足我们的生活需要吗?
是整数吗?
是分数吗?
是多少?
它是一个无限不循环小数
=1.41421356…
然而,第一个发现这样的数的人却被抛进大海,你想知道这其中的曲折离奇吗?这得追溯到2500年前,有个叫毕达哥拉斯的人,他是一个伟大的数学家,他创立了毕达哥拉斯学派,这是一个非常神秘的学派,他们以领袖毕达哥拉斯为核心,认为毕达哥拉斯是至高无尚的,他所说的一切都是真理。
毕达哥拉斯( Pythagoras) 认为“宇宙间的一切现象都能归结为整数或整数之比,即都可用有理数来描述。
但后来,这学派的一位年轻成员希伯索斯(Hippasus) 发现边长为1的正方形的对角线的长不能用有理数来表示,这就动摇了毕达哥拉斯学派的信条,引起了信徒们的恐慌,他们试图封锁这一发现,然而希伯索斯偷偷将这一发现传播出去,这为他招来了杀身之祸,在他逃回家的路上,遭到毕氏成员的围捕,被投入大海。
他这一死,使得这类数的计算推迟了500多年,给数学的发展造成了不可弥补的损失。
1
1
1
C
B
A
b
b是有理数吗?
你能设法用多种方法找出几个这样的非有理数吗?请说明理由.
(1)面积为5、8、10等非平方数的正方形的边长;
(2)边长为2的等边三角形的高;
(3)通过构造直角三角形;
(4)列方程.如x =3.等等
议一议
跟踪训练
(1)、在数0, 1, ,0.1235中,无理数的个数为( )
A.0个 B.1个 C.2个 D.3个
(2)、下列各数3.14, ,0, ,3.1414414441…
(相邻两个1之间4的个数逐次加1)中,( )是有理数,( )是无理数。
(3)、边长为2的正方形的对角线是( )
A.整数 B.有理数 C.分数 D.无理数
如图是由16个边长为1的小正方形拼成的,任意连接这些小正方形的若干个顶点,可得到一些线段.
试一试
(1)每人至少找出3条长度为非有理数
的线段;
(2)最长的非有理数线段是哪一条?
最短的非有理数线段
是哪一条?为什么?
温馨提示:带根号的数并不都是无理数,反之,无理数也并非都带根号。判断一个数是不是无理数,应从定义出发,看它是不是无限不循环小数。
温馨提示:有理数与无理数的区别:有理数包括整数和分数,而分数都可化成有限小数和无限循环小数的形式;把有理数和无理数都写成小数形式时,有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数。
2、下列说法:(1)有理数都是有限小数
(2)有限小数都是有理数
(3)无理数都是无限小数
(4)无限小数都是无理数,
其中正确的为______________________________。
3、一个面积为13cm2的正方形,它的边长是________
4、已知正数m满足m2=39,则m的整数部分是_________
给出单位长度为1的线段,你会做出长度为的线段吗?会做出长度分别为 与 的线段吗?
(1)如下图,OA=OB,数轴上A点对应的数是什么?
它介于哪两个整数之间?
(2)如果将所有有理数都标到数轴上,那么数轴被
填满了吗?
-2
-1
0
1
2
B
A
无理数跟有理数一样,也可以用数轴上的点表示,这是对无理数的几何解释。
温馨提示:
并不是所有的无理数都能用尺规作图的方法在数轴上作出它对应的点。
3、在数轴上作出 对应的点。
-2
-1
0
1
2
达标测评:
1、选择题:(1)、做一个边长为13平方厘米的正方形,它的边长是( )
A、一个整数 B、一个分数 C、一个有理数 D、一个无理数
(2)、在实数0,1,0.1235, 中,无理数的个数为( )
A、0个 B、1个 C、2个 D、3个
2、填空题:
(3)、写出一个比 小的整数( )
(4)、无理数可以利用数轴上的点表示,数轴上的点表示的( )是无理数(填“一定”或“不一定”)
课堂小结:
1、体验无理数的几何解释,明白数轴上有些点表示有理数,有些表示无理数,加深对数轴的认识。
2、要综合运用勾股定理和算术平方根、无理数等知识来求两点间距离,注意仔细观察以及数形结合思想的运用。
1
1
毕达哥拉斯树
螺形图
欣赏有趣的图形:
点击
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
