变量间的相互关系与统计案例
图片预览











文档简介
(共78张PPT)
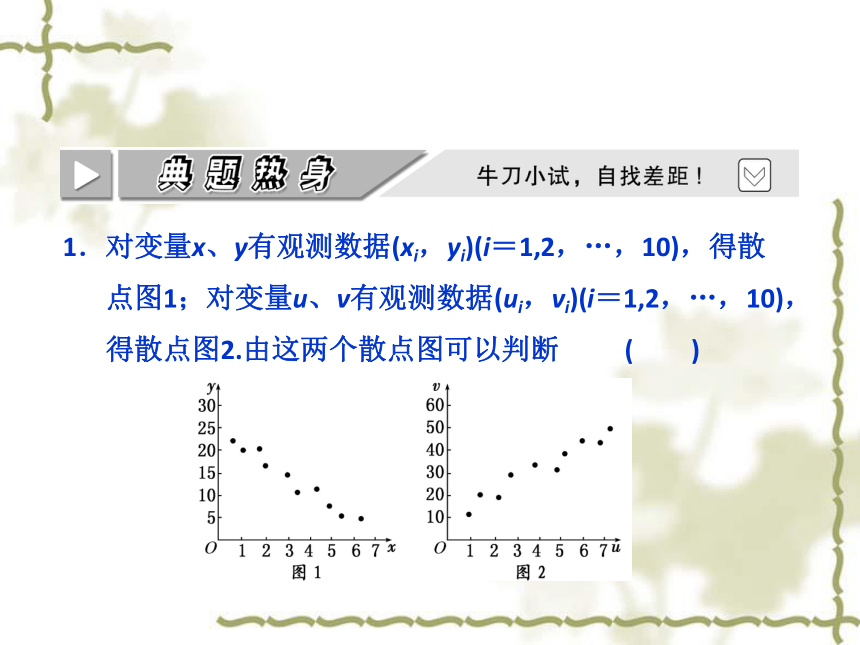
1.对变量x、y有观测数据(xi,yi)(i=1,2,…,10),得散
点图1;对变量u、v有观测数据(ui,vi)(i=1,2,…,10),得散点图2.由这两个散点图可以判断 ( )
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
解析:由图1可知,各点整体呈递减趋势,x与y负相关.由图2可知,各点整体呈递增趋势,u与v正相关.
答案:C
解析:由图象知选项B、D为正相关,选项C不符合实
际意义.
答案:A
3.在第29届北京奥运会上,中国健儿取得了51金、21银、
28铜的好成绩,稳居金牌榜榜首,由此许多人认为中
国进入了世界体育强国之列,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中
有1560名持反对意见,2452名女性中有1200名持反对
意见,在运用这些数据说明性别对判断“中国进入了
世界体育强国之列”是否有关系时,用什么方法最有
说服力 ( )
A.平均数与方差 B.回归直线方程
C.独立性检验 D.概率
解析:由于参加调查的公民按性别被分成了两组,而且每一组又被分成了两种情况,认为有关与无关,符合2×2列联表的要求,故用独立性检验最有说服力.
答案:C
4.下面是一个2×2列联表
则表中n11、n+1的值分别为________.
解析:∵n11+21=73,∴n11=52.
又∵n11+2=n+1,∴n+1=54.
答案:52、54
y1 y2 合计
x1 n11 21 73
x2 2 25 27
合计 n+1 46
5.春节期间,某市物价部门,对本市五个商场销售的某
商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如下表所示:
价格x 9 9.5 10 10.5 11
销售量y 11 10 8 6 5
通过分析,发现销售量y对商品的价格x具有线性相关关系,则销售量y对商品的价格x的回归直线方程为________________________.
1.两个变量的线性相关
(1)正相关.
在散点图中,点散布在从 到 的区域,
对于两个变量的这种相关关系,我们将它称为正相关.
左下角
右上角
(2)负相关.
在散点图中,点散布在从 到 的区域,两个变量的这种相关关系称为负相关.
(3)线性相关关系、回归直线.如果散点图中点的分布从整体上看大致在 ,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
左上角
右下角
一条直线附近
2.回归方程
(1)最小二乘法
求回归直线使得样本数据的点到它的 的方法叫做最小二乘法.
距离的平方和最小
R2越大,意味着残差平方和 ,即模型的拟合效果 好.R2越小,残差平方和 ,即模型的拟合效果 .在线性回归模型中,R2表示解释变量对于预报变量变化的贡献率,R2越接近于1,表示回归的效果 .
越小
越
越大
越差
越好
4.独立性检验
(1)分类变量:变量的不同“值”表示个体所属的 ,像这类变量称为分类变量.
(2)列联表:列出两个分类变量
的 ,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为
不同类别
频数表
2×2列联表
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
a+b+c+d
(2010·广东高考)某市居民2005~2009年家庭年平均收入x(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:
考点一 两个变量的相关关系
[自主解答] 居民家庭的年平均收入按从小到大排依次为:11.5、12.1、13、13.3、15,由中位数定义知年平均收入的中位数是13.画出散点图,由图可知家庭年平均收入与年平均支出有正的线性相关关系.
[答案] 13 正
年份 2005 2006 2007 2008 2009
收入x 11.5 12.1 13 13.3 15
支出Y 6.8 8.8 9.8 10 12
根据统计资料,居民家庭年平均收入的中位数是_______,家庭年平均收入与年平均支出有______线性相关关系.
下面是水稻产量与施化肥量的一组观测数据:
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
施化肥量 15 20 25 30 35 40 45
水稻产量 320 330 360 410 460 470 480
解:(1)散点图如下:
(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量由小变大,图中的数据点大致分布在一条直线的附近,因此施化肥量和水稻产量近似成线性相关关系,但水稻产量只是在一定范围内随着化肥施用量的增加而增长.
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
考点二 线性回归分析
日期 1月
10日 2月
10日 3月
10日 4月
10日 5月
10日 6月
10日
昼夜温差
x(℃) 10 11 13 12 8 6
就诊人数
y(个) 22 25 29 26 16 12
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
零件数x(个) 10 20 30 40 50 60 70 80 90 100
加工时间y(分) 62 68 75 81 89 95 102 108 115 122
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
解:(1)列出下表:
i 1 2 3 4 5 6 7 8 9 10
xi 10 20 30 40 50 60 70 80 90 100
yi 62 68 75 81 89 95 102 108 115 122
xiyi 620 1 360 2 250 3 240 4 450 5 700 7 140 8 640 10 350 12 200
(2010·全国新课标)为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
考点三 独立性检验
性别
是否需要志愿者 男 女
需要 40 30
不需要 160 270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
附:
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法,比采用简单随机抽样方法更好.
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断性别与休闲方式是否有关系.
解:(1)2×2列联表如下:
休闲方式
性别 看电视 运动 总计
女 43 27 70
男 21 33 54
总计 64 60 124
高考对本节内容的考查主要是线性回归分析和独立性检验的统计分析方法,题型多为选择题和填空题,近几年2×2列联表及独立性检验问题频率较高的出现在高考试题中,并成为一种重要考查方向.
[考题印证] (2010·辽宁高考)(13分)为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.下表1和表2分别是注射药物A和药物B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积 [60,65) [65,70) [70,75) [75,80)
频数 30 40 20 10
表2:注射药物B后皮肤疱疹面积的频数分布表
疱疹面积 [60,65) [65,70) [70,75) [75,80) [80,85)
频数 10 25 20 30 15
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为
“注射药物A后的疱疹面积与注射药物B后的疱疹面积有
差异”.
表3:
疱疹面积小于70mm2 疱疹面积不小于70mm2 合计
注射药物A a= b=
注射药物B c= d=
合计 n=
P(K2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
[规范解答] (1)
…………………………………………… ……… (3分)
从频率分布直方图中可以看出注射药物A后皮肤疱疹面积的中位数在65至70之间 ,而注射药物B后皮肤疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.…………(6分)
(2)表3:
疱疹面积小于70mm2 疱疹面积不小于70mm2 合计
注射药物A a=70 b=30 100
注射药物B c=35 d=65 100
合计 105 95 n=200
1.线性相关关系的理解
相关关系与函数关系不同.函数关系中的两个变量间是一种确定性关系.例如正方形面积S与边长x之间的关系S=x2就是函数关系.相关关系是一种非确定性关系,即相关关系是非随机变量与随机变量之间的关系.例如商品的销售额与广告费是相关关系.两个变量具有相关关系是回归分析的前提.
3.回归分析的应用
回归分析是处理变量相关关系的一种数学方法.主要解决:(1)确定特定量之间是否有相关关系,如果有就找出它们之间贴近的数学表达式;(2)根据一组观察值,预测变量的取值及判断变量取值的变化趋势;(3)求出回归直线方程.
1.下列有关线性回归的说法,不正确的是 ( )
A.相关关系的两个变量不一定是因果关系
B.散点图能直观地反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任一组数据都有回归直线方程
.
解析:根据两个变量属相关关系的概念,可知A正确,散点图能直观地描述呈相关关系的两个变量的相关程度,且回归直线最能代表它们之间的相关关系,所以B、C正确.只有线性相关的数据才有回归直线方程,所以D不正确.
答案:D
2.对两个变量y与x进行回归分析,分别选择不同的模型,
它们的相关系数r如下,其中拟合效果最好的模型是
( )
A.模型Ⅰ的相关系数r为0.98
B.模型Ⅱ的相关系数r为0.80
C.模型Ⅲ的相关系数r为0.50
D.模型Ⅳ的相关系数r为0.25
解析:根据相关系数的定义和计算公式可知,|r|≤1,且|r|越接近于1,相关程度越大,拟合效果越好;|r|越接近于0,相关程度越小,拟合效果越弱,所以A正确.
答案:A
3.分类变量X和Y的列联表如下:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
则下列说法正确的是 ( )
A.ad-bc越小,说明X与Y关系越弱
B.ad-bc越大,说明X与Y关系越弱
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强
解析:对于同一样本,|ad-bc|越小,说明X与Y之间关系越弱;|ad-bc|越大,说明X与Y之间的关系越强.
答案:C
4.(2011·马鞍山模拟)某高校“统计初步”课程的教师随机
调查了选该课程的一些学生的情况,具体数据如下表:
专业
性别 非统计专业 统计专业
男 13 10
女 7 20
解析:∵K2≈4.844>3.841,∴有95%的把握认为主修统计专业与性别有关系,即作出“主修统计专业与性别有关
系”的判断,出错的可能性不超过5%.
答案:5%
5.某服装商场为了了解毛衣的月销售量y(件)与月平均气温
x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
答案:46
6.一台机器使用时间较长,但还可以使用.它按不同的
转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,下表为抽样试验结果:
转速x(转/秒) 16 14 12 8
每小时生产有缺
点的零件数y(件) 11 9 8 5
(1)对变量y与x进行相关性检验;
(2)如果y与x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
点击此图片进入课下冲关作业
1.对变量x、y有观测数据(xi,yi)(i=1,2,…,10),得散
点图1;对变量u、v有观测数据(ui,vi)(i=1,2,…,10),得散点图2.由这两个散点图可以判断 ( )
A.变量x与y正相关,u与v正相关
B.变量x与y正相关,u与v负相关
C.变量x与y负相关,u与v正相关
D.变量x与y负相关,u与v负相关
解析:由图1可知,各点整体呈递减趋势,x与y负相关.由图2可知,各点整体呈递增趋势,u与v正相关.
答案:C
解析:由图象知选项B、D为正相关,选项C不符合实
际意义.
答案:A
3.在第29届北京奥运会上,中国健儿取得了51金、21银、
28铜的好成绩,稳居金牌榜榜首,由此许多人认为中
国进入了世界体育强国之列,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中
有1560名持反对意见,2452名女性中有1200名持反对
意见,在运用这些数据说明性别对判断“中国进入了
世界体育强国之列”是否有关系时,用什么方法最有
说服力 ( )
A.平均数与方差 B.回归直线方程
C.独立性检验 D.概率
解析:由于参加调查的公民按性别被分成了两组,而且每一组又被分成了两种情况,认为有关与无关,符合2×2列联表的要求,故用独立性检验最有说服力.
答案:C
4.下面是一个2×2列联表
则表中n11、n+1的值分别为________.
解析:∵n11+21=73,∴n11=52.
又∵n11+2=n+1,∴n+1=54.
答案:52、54
y1 y2 合计
x1 n11 21 73
x2 2 25 27
合计 n+1 46
5.春节期间,某市物价部门,对本市五个商场销售的某
商品一天的销售量及其价格进行调查,五个商场的售价x元和销售量y件之间的一组数据如下表所示:
价格x 9 9.5 10 10.5 11
销售量y 11 10 8 6 5
通过分析,发现销售量y对商品的价格x具有线性相关关系,则销售量y对商品的价格x的回归直线方程为________________________.
1.两个变量的线性相关
(1)正相关.
在散点图中,点散布在从 到 的区域,
对于两个变量的这种相关关系,我们将它称为正相关.
左下角
右上角
(2)负相关.
在散点图中,点散布在从 到 的区域,两个变量的这种相关关系称为负相关.
(3)线性相关关系、回归直线.如果散点图中点的分布从整体上看大致在 ,就称这两个变量之间具有线性相关关系,这条直线叫做回归直线.
左上角
右下角
一条直线附近
2.回归方程
(1)最小二乘法
求回归直线使得样本数据的点到它的 的方法叫做最小二乘法.
距离的平方和最小
R2越大,意味着残差平方和 ,即模型的拟合效果 好.R2越小,残差平方和 ,即模型的拟合效果 .在线性回归模型中,R2表示解释变量对于预报变量变化的贡献率,R2越接近于1,表示回归的效果 .
越小
越
越大
越差
越好
4.独立性检验
(1)分类变量:变量的不同“值”表示个体所属的 ,像这类变量称为分类变量.
(2)列联表:列出两个分类变量
的 ,称为列联表.假设有两个分类变量X和Y,它们的可能取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为
不同类别
频数表
2×2列联表
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
a+b+c+d
(2010·广东高考)某市居民2005~2009年家庭年平均收入x(单位:万元)与年平均支出Y(单位:万元)的统计资料如下表所示:
考点一 两个变量的相关关系
[自主解答] 居民家庭的年平均收入按从小到大排依次为:11.5、12.1、13、13.3、15,由中位数定义知年平均收入的中位数是13.画出散点图,由图可知家庭年平均收入与年平均支出有正的线性相关关系.
[答案] 13 正
年份 2005 2006 2007 2008 2009
收入x 11.5 12.1 13 13.3 15
支出Y 6.8 8.8 9.8 10 12
根据统计资料,居民家庭年平均收入的中位数是_______,家庭年平均收入与年平均支出有______线性相关关系.
下面是水稻产量与施化肥量的一组观测数据:
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
施化肥量 15 20 25 30 35 40 45
水稻产量 320 330 360 410 460 470 480
解:(1)散点图如下:
(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量由小变大,图中的数据点大致分布在一条直线的附近,因此施化肥量和水稻产量近似成线性相关关系,但水稻产量只是在一定范围内随着化肥施用量的增加而增长.
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
考点二 线性回归分析
日期 1月
10日 2月
10日 3月
10日 4月
10日 5月
10日 6月
10日
昼夜温差
x(℃) 10 11 13 12 8 6
就诊人数
y(个) 22 25 29 26 16 12
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
零件数x(个) 10 20 30 40 50 60 70 80 90 100
加工时间y(分) 62 68 75 81 89 95 102 108 115 122
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
解:(1)列出下表:
i 1 2 3 4 5 6 7 8 9 10
xi 10 20 30 40 50 60 70 80 90 100
yi 62 68 75 81 89 95 102 108 115 122
xiyi 620 1 360 2 250 3 240 4 450 5 700 7 140 8 640 10 350 12 200
(2010·全国新课标)为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
考点三 独立性检验
性别
是否需要志愿者 男 女
需要 40 30
不需要 160 270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
P(K2≥k) 0.050 0.010 0.001
k 3.841 6.635 10.828
附:
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法,比采用简单随机抽样方法更好.
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2列联表;
(2)判断性别与休闲方式是否有关系.
解:(1)2×2列联表如下:
休闲方式
性别 看电视 运动 总计
女 43 27 70
男 21 33 54
总计 64 60 124
高考对本节内容的考查主要是线性回归分析和独立性检验的统计分析方法,题型多为选择题和填空题,近几年2×2列联表及独立性检验问题频率较高的出现在高考试题中,并成为一种重要考查方向.
[考题印证] (2010·辽宁高考)(13分)为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物A,另一组注射药物B.下表1和表2分别是注射药物A和药物B后的试验结果.(疱疹面积单位:mm2)
表1:注射药物A后皮肤疱疹面积的频数分布表
疱疹面积 [60,65) [65,70) [70,75) [75,80)
频数 30 40 20 10
表2:注射药物B后皮肤疱疹面积的频数分布表
疱疹面积 [60,65) [65,70) [70,75) [75,80) [80,85)
频数 10 25 20 30 15
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为
“注射药物A后的疱疹面积与注射药物B后的疱疹面积有
差异”.
表3:
疱疹面积小于70mm2 疱疹面积不小于70mm2 合计
注射药物A a= b=
注射药物B c= d=
合计 n=
P(K2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
[规范解答] (1)
…………………………………………… ……… (3分)
从频率分布直方图中可以看出注射药物A后皮肤疱疹面积的中位数在65至70之间 ,而注射药物B后皮肤疱疹面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.…………(6分)
(2)表3:
疱疹面积小于70mm2 疱疹面积不小于70mm2 合计
注射药物A a=70 b=30 100
注射药物B c=35 d=65 100
合计 105 95 n=200
1.线性相关关系的理解
相关关系与函数关系不同.函数关系中的两个变量间是一种确定性关系.例如正方形面积S与边长x之间的关系S=x2就是函数关系.相关关系是一种非确定性关系,即相关关系是非随机变量与随机变量之间的关系.例如商品的销售额与广告费是相关关系.两个变量具有相关关系是回归分析的前提.
3.回归分析的应用
回归分析是处理变量相关关系的一种数学方法.主要解决:(1)确定特定量之间是否有相关关系,如果有就找出它们之间贴近的数学表达式;(2)根据一组观察值,预测变量的取值及判断变量取值的变化趋势;(3)求出回归直线方程.
1.下列有关线性回归的说法,不正确的是 ( )
A.相关关系的两个变量不一定是因果关系
B.散点图能直观地反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任一组数据都有回归直线方程
.
解析:根据两个变量属相关关系的概念,可知A正确,散点图能直观地描述呈相关关系的两个变量的相关程度,且回归直线最能代表它们之间的相关关系,所以B、C正确.只有线性相关的数据才有回归直线方程,所以D不正确.
答案:D
2.对两个变量y与x进行回归分析,分别选择不同的模型,
它们的相关系数r如下,其中拟合效果最好的模型是
( )
A.模型Ⅰ的相关系数r为0.98
B.模型Ⅱ的相关系数r为0.80
C.模型Ⅲ的相关系数r为0.50
D.模型Ⅳ的相关系数r为0.25
解析:根据相关系数的定义和计算公式可知,|r|≤1,且|r|越接近于1,相关程度越大,拟合效果越好;|r|越接近于0,相关程度越小,拟合效果越弱,所以A正确.
答案:A
3.分类变量X和Y的列联表如下:
y1 y2 总计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
则下列说法正确的是 ( )
A.ad-bc越小,说明X与Y关系越弱
B.ad-bc越大,说明X与Y关系越弱
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强
解析:对于同一样本,|ad-bc|越小,说明X与Y之间关系越弱;|ad-bc|越大,说明X与Y之间的关系越强.
答案:C
4.(2011·马鞍山模拟)某高校“统计初步”课程的教师随机
调查了选该课程的一些学生的情况,具体数据如下表:
专业
性别 非统计专业 统计专业
男 13 10
女 7 20
解析:∵K2≈4.844>3.841,∴有95%的把握认为主修统计专业与性别有关系,即作出“主修统计专业与性别有关
系”的判断,出错的可能性不超过5%.
答案:5%
5.某服装商场为了了解毛衣的月销售量y(件)与月平均气温
x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温x(℃) 17 13 8 2
月销售量y(件) 24 33 40 55
答案:46
6.一台机器使用时间较长,但还可以使用.它按不同的
转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器运转的速度而变化,下表为抽样试验结果:
转速x(转/秒) 16 14 12 8
每小时生产有缺
点的零件数y(件) 11 9 8 5
(1)对变量y与x进行相关性检验;
(2)如果y与x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
点击此图片进入课下冲关作业
