五年级下册数学教案 3.2 列方程解决问题(四) 沪教版 (1)(表格式)
文档属性
| 名称 | 五年级下册数学教案 3.2 列方程解决问题(四) 沪教版 (1)(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 31.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览

文档简介
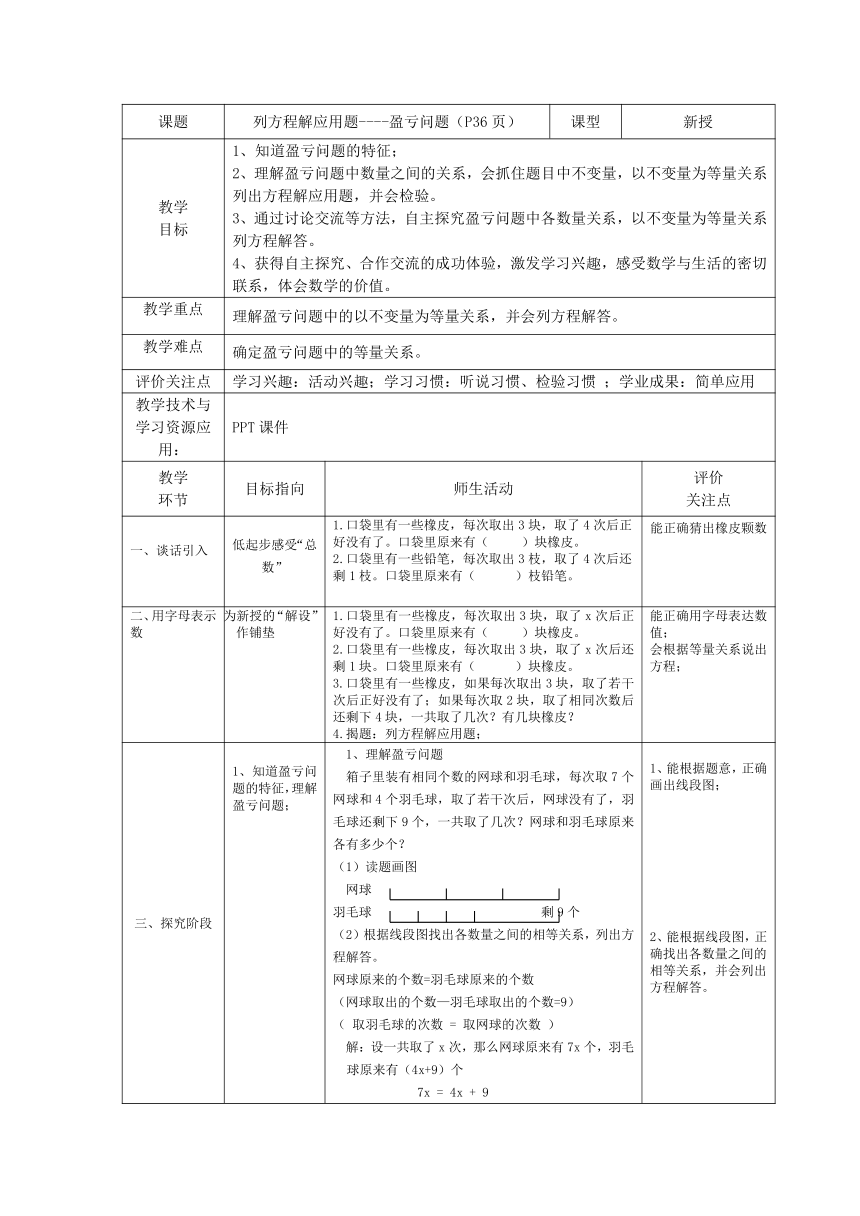
课题
列方程解应用题----盈亏问题(P36页)
课型
新授
教学
目标
1、知道盈亏问题的特征;
2、理解盈亏问题中数量之间的关系,会抓住题目中不变量,以不变量为等量关系列出方程解应用题,并会检验。
3、通过讨论交流等方法,自主探究盈亏问题中各数量关系,以不变量为等量关系列方程解答。
4、获得自主探究、合作交流的成功体验,激发学习兴趣,感受数学与生活的密切联系,体会数学的价值。
教学重点
理解盈亏问题中的以不变量为等量关系,并会列方程解答。
教学难点
确定盈亏问题中的等量关系。
评价关注点
学习兴趣:活动兴趣;学习习惯:听说习惯、检验习惯
;学业成果:简单应用
教学技术与学习资源应用:
PPT课件
教学
环节
目标指向
师生活动
评价
关注点
一、谈话引入
低起步感受“总数”
1.口袋里有一些橡皮,每次取出3块,取了4次后正好没有了。口袋里原来有(
)块橡皮。
2.口袋里有一些铅笔,每次取出3枝,取了4次后还剩1枝。口袋里原来有(
)枝铅笔。
能正确猜出橡皮颗数
二、用字母表示数
为新授的“解设”作铺垫
1.口袋里有一些橡皮,每次取出3块,取了x次后正好没有了。口袋里原来有(
)块橡皮。
2.口袋里有一些橡皮,每次取出3块,取了x次后还剩1块。口袋里原来有(
)块橡皮。
3.口袋里有一些橡皮,如果每次取出3块,取了若干次后正好没有了;如果每次取2块,取了相同次数后还剩下4块,一共取了几次?有几块橡皮?
4.揭题:列方程解应用题;
能正确用字母表达数值;
会根据等量关系说出方程;
三、探究阶段
1、知道盈亏问题的特征,理解盈亏问题;
2、找出数量关系,会抓住题目中不变量,以不变量为等量关系列出方程解应用题,并会检验。
1、理解盈亏问题
箱子里装有相同个数的网球和羽毛球,每次取7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩下9个,一共取了几次?网球和羽毛球原来各有多少个?
(1)读题画图
网球
羽毛球
剩9个
(2)根据线段图找出各数量之间的相等关系,列出方程解答。
网球原来的个数=羽毛球原来的个数
(网球取出的个数—羽毛球取出的个数=9)
(
取羽毛球的次数
=
取网球的次数
)
解:设一共取了x次,那么网球原来有7x个,羽毛球原来有(4x+9)个
7x
=
4x
+
9
7x—4x
=
9
解:设网球和羽毛球原来各有x个,那么网球一共取了
(x÷7)次,羽毛球一共取了【(x—9)÷4】次
x÷7=(x—9)÷4
(3)你是怎样找等量关系列方程的?
在小组里交流。
1、能根据题意,正确画出线段图;
2、能根据线段图,正确找出各数量之间的相等关系,并会列出方程解答。
四、运用阶段
1、巩固确定盈亏问题中的等量关系。
1、模仿练习
盒子里装有相同个数的水果糖和棒棒糖,每次取出5个水果糖和3个棒棒糖,取了若干次后,水果糖没有了,棒棒糖还剩下6个,一共取了几次?水果糖和棒棒糖原来各有多少个?
1、能根据题意,正确列方程解答;
2、能选出正确的方程。
五、综合练习
1、通过各类练习巩固所学知识;
2、运用盈亏问题中的以不变量为等量关系,列方程解答。
一、判断题:
(1)盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩下6个。一共取了几次?红球和白球原来各有多少个?
解:设一共取了X次。
5X=3X-6
2X=6
X=3
5X=5×3=15
答:一共取了3次,红球和白球各有15个。
(
×
)
二、选择题
(1)五(1)班男生和女生人数一样多,每组4名男生和5名女生,分了若干组后,男生还剩6人,女生还剩2人,一共分了几组?解:设一共分了x组,下列方程正确的是(
)
(1)4x+6=5x;
(2)4x+6=5x+2;(3)4x+6=5x-2
(2)故事书和科技书一样多,分给小朋友。故事书每人分3本,则余6本;科技书每人分4本,则缺12本,问小朋友有几人?
解:设小朋友有x人,正确的方程是(
)
(1)3x-6=5x-12
(2)3x+6=4x+12
(3)3x+6=4x-12
三、填空题
(1)小巧和小亚有一样多的零用钱,小巧买了3瓶可乐,钱正好用完;小亚想买5瓶同样的可乐,但缺8元,可乐多少元一瓶?小巧和小亚原来各有多少元?
(2)小巧和小亚有一样多的零用钱,小巧买了3元一瓶的冰红茶,钱正好用完;小亚买了5元一瓶的橙汁,比小巧少买了8瓶,小巧和小亚各买了多少瓶?
四、列方程、不解答
(1)甲厂用相同的巴士组织工人春游,如每车坐45人,则有20人不能乘车;如每车坐50人,正好坐满。问共有几辆巴士?共有多少工人?
(2)乙厂用相同的巴士组织工人春游,如每车坐45人,则有20人不能乘车;如每车坐50人,则有10个空位。问共有几辆巴士?共有多少工人?
(3)丙厂用相同的巴士组织工人春游,如每车坐45人,则缺少20个座位;
如每车坐50人,恰好多余一辆车。问共有几辆汽车?共有多少工人?
对“还剩下”能正确运用符号表示;
在复杂的情况下,能看清等量关系;
六、全课总结
这节课有什么收获?
做这类题的关键是什么?
(列方程解应用题的关键是找相等的量)
解题时应该注意点什么?
板
书
设
计
列方程解应用题
网球原来的个数
=
羽毛球原来的个数
解:
设一共取了x次,那么网球原来有7
x个,羽毛球原来有(4
x+9)个。
7
x
=
4
x+9
7
x-4
x
=
9
3
x
=
9
x
=
3
7
x=7×3=21(或4
x+9=4×3+9=21).
答:一共取了3次,网球和羽毛球原来各有21个。
非书面作业设计
教学反思
列方程解应用题----盈亏问题(P36页)
课型
新授
教学
目标
1、知道盈亏问题的特征;
2、理解盈亏问题中数量之间的关系,会抓住题目中不变量,以不变量为等量关系列出方程解应用题,并会检验。
3、通过讨论交流等方法,自主探究盈亏问题中各数量关系,以不变量为等量关系列方程解答。
4、获得自主探究、合作交流的成功体验,激发学习兴趣,感受数学与生活的密切联系,体会数学的价值。
教学重点
理解盈亏问题中的以不变量为等量关系,并会列方程解答。
教学难点
确定盈亏问题中的等量关系。
评价关注点
学习兴趣:活动兴趣;学习习惯:听说习惯、检验习惯
;学业成果:简单应用
教学技术与学习资源应用:
PPT课件
教学
环节
目标指向
师生活动
评价
关注点
一、谈话引入
低起步感受“总数”
1.口袋里有一些橡皮,每次取出3块,取了4次后正好没有了。口袋里原来有(
)块橡皮。
2.口袋里有一些铅笔,每次取出3枝,取了4次后还剩1枝。口袋里原来有(
)枝铅笔。
能正确猜出橡皮颗数
二、用字母表示数
为新授的“解设”作铺垫
1.口袋里有一些橡皮,每次取出3块,取了x次后正好没有了。口袋里原来有(
)块橡皮。
2.口袋里有一些橡皮,每次取出3块,取了x次后还剩1块。口袋里原来有(
)块橡皮。
3.口袋里有一些橡皮,如果每次取出3块,取了若干次后正好没有了;如果每次取2块,取了相同次数后还剩下4块,一共取了几次?有几块橡皮?
4.揭题:列方程解应用题;
能正确用字母表达数值;
会根据等量关系说出方程;
三、探究阶段
1、知道盈亏问题的特征,理解盈亏问题;
2、找出数量关系,会抓住题目中不变量,以不变量为等量关系列出方程解应用题,并会检验。
1、理解盈亏问题
箱子里装有相同个数的网球和羽毛球,每次取7个网球和4个羽毛球,取了若干次后,网球没有了,羽毛球还剩下9个,一共取了几次?网球和羽毛球原来各有多少个?
(1)读题画图
网球
羽毛球
剩9个
(2)根据线段图找出各数量之间的相等关系,列出方程解答。
网球原来的个数=羽毛球原来的个数
(网球取出的个数—羽毛球取出的个数=9)
(
取羽毛球的次数
=
取网球的次数
)
解:设一共取了x次,那么网球原来有7x个,羽毛球原来有(4x+9)个
7x
=
4x
+
9
7x—4x
=
9
解:设网球和羽毛球原来各有x个,那么网球一共取了
(x÷7)次,羽毛球一共取了【(x—9)÷4】次
x÷7=(x—9)÷4
(3)你是怎样找等量关系列方程的?
在小组里交流。
1、能根据题意,正确画出线段图;
2、能根据线段图,正确找出各数量之间的相等关系,并会列出方程解答。
四、运用阶段
1、巩固确定盈亏问题中的等量关系。
1、模仿练习
盒子里装有相同个数的水果糖和棒棒糖,每次取出5个水果糖和3个棒棒糖,取了若干次后,水果糖没有了,棒棒糖还剩下6个,一共取了几次?水果糖和棒棒糖原来各有多少个?
1、能根据题意,正确列方程解答;
2、能选出正确的方程。
五、综合练习
1、通过各类练习巩固所学知识;
2、运用盈亏问题中的以不变量为等量关系,列方程解答。
一、判断题:
(1)盒子里的红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩下6个。一共取了几次?红球和白球原来各有多少个?
解:设一共取了X次。
5X=3X-6
2X=6
X=3
5X=5×3=15
答:一共取了3次,红球和白球各有15个。
(
×
)
二、选择题
(1)五(1)班男生和女生人数一样多,每组4名男生和5名女生,分了若干组后,男生还剩6人,女生还剩2人,一共分了几组?解:设一共分了x组,下列方程正确的是(
)
(1)4x+6=5x;
(2)4x+6=5x+2;(3)4x+6=5x-2
(2)故事书和科技书一样多,分给小朋友。故事书每人分3本,则余6本;科技书每人分4本,则缺12本,问小朋友有几人?
解:设小朋友有x人,正确的方程是(
)
(1)3x-6=5x-12
(2)3x+6=4x+12
(3)3x+6=4x-12
三、填空题
(1)小巧和小亚有一样多的零用钱,小巧买了3瓶可乐,钱正好用完;小亚想买5瓶同样的可乐,但缺8元,可乐多少元一瓶?小巧和小亚原来各有多少元?
(2)小巧和小亚有一样多的零用钱,小巧买了3元一瓶的冰红茶,钱正好用完;小亚买了5元一瓶的橙汁,比小巧少买了8瓶,小巧和小亚各买了多少瓶?
四、列方程、不解答
(1)甲厂用相同的巴士组织工人春游,如每车坐45人,则有20人不能乘车;如每车坐50人,正好坐满。问共有几辆巴士?共有多少工人?
(2)乙厂用相同的巴士组织工人春游,如每车坐45人,则有20人不能乘车;如每车坐50人,则有10个空位。问共有几辆巴士?共有多少工人?
(3)丙厂用相同的巴士组织工人春游,如每车坐45人,则缺少20个座位;
如每车坐50人,恰好多余一辆车。问共有几辆汽车?共有多少工人?
对“还剩下”能正确运用符号表示;
在复杂的情况下,能看清等量关系;
六、全课总结
这节课有什么收获?
做这类题的关键是什么?
(列方程解应用题的关键是找相等的量)
解题时应该注意点什么?
板
书
设
计
列方程解应用题
网球原来的个数
=
羽毛球原来的个数
解:
设一共取了x次,那么网球原来有7
x个,羽毛球原来有(4
x+9)个。
7
x
=
4
x+9
7
x-4
x
=
9
3
x
=
9
x
=
3
7
x=7×3=21(或4
x+9=4×3+9=21).
答:一共取了3次,网球和羽毛球原来各有21个。
非书面作业设计
教学反思
