【同步必刷题】2.1 空间点、直线、平面之间的位置关系 基础练(含解析)
文档属性
| 名称 | 【同步必刷题】2.1 空间点、直线、平面之间的位置关系 基础练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:08:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题基础练
第二章《点、直线、平面之间的位置关系》
2.1
空间点、直线、平面之间的位置关系
一.选择题
1.(2021?二模拟)正方体ABCD﹣A1B1C1D1中,E,F分别为D1C1,BB1的中点,则异面直线AE,FC所成的角的余弦值为( )
A.
B.
C.
D.
2.(2021?五模拟)在正方体ABCD﹣A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则CM与D1N所成角的正切值为( )
A.
B.
C.4
D.﹣4
3.(2020秋?香坊区校级期末)已知三个不同的平面α,β,γ,三条不重合的直线m,n,l,有下列四个命题:
①若m⊥l,n⊥l,则m∥n;
②若α⊥γ,β⊥γ,则α∥β;
③若m⊥α,m∥n,n?β,则α⊥β;
④若m∥α,α∩β=n,则m∥n
其中真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
4.(2020秋?皇姑区校级期末)如图所示,设E、F分别是正方体ABCD﹣A1B1C1D1的棱CD上两点,且AB=2,EF=1,其中正确的命题为( )
A.异面直线B1D1与EF所成的角为45°
B.异面直线B1D1与EF所成的角为30°
C.直线B1D1与平面B1EF所成的角为45°
D.直线B1D1与平面B1EF所成的角为60°
5.(2020秋?香坊区校级期末)已知三个不同的平面α,β,γ,三条不重合的直线m,n,l,有下列四个命题中正确的是( )
A.若m⊥l,n⊥l,则m∥n
B.若a⊥γ,β⊥γ,则α∥β
C.若m⊥α,m∥n,n?β,则α⊥β
D.若m∥α,α∩β=n,则m∥n
6.(2020秋?朝阳区校级期末)在直棱柱ABC﹣A1B1C1中,AB⊥BC,其中AB=BC=BB1=2,点D是AC的中点,则异面直线AB1与BD所成角的大小为( )
A.
B.
C.
D.
7.(2020秋?城关区校级期末)已知l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,则下列命题中不正确的是( )
A.若α∥β,则m⊥α
B.若α∥β,则l⊥m
C.若l⊥m,则l∥β
D.若m∥α,则α⊥β
二.填空题
8.(2021?闵行区一模)如图,已知正四棱柱ABCD﹣A1B1C1D1的底面边长为2,高为3,则异面直线AA1与BD1所成角的大小是
.
9.(2020秋?宝应县月考)四棱锥P﹣ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=4,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是
.
10.(2020秋?秦都区校级月考)已知直线m∥平面α,直线n在α内,则m与n所有可能的位置关系是
.
11.(2020秋?海曙区校级期中)已知直三棱柱ABC﹣A1B1C1中,∠ABC=90°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的正弦值为
.
12.(2020秋?闵行区校级期末)设E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,若AC⊥BD,则四边形EFGH的形状是
.
13.(2020秋?闵行区校级期末)在所有经过正方体ABCD﹣A1B1C1D1的任意两个顶点的直线中任取k条,求这k条直线恰是两两异面,则k的最大值为
.
14.(2021?十三模拟)如图,在多面体ABCDEF中,四边形ABCD为正方形,ED⊥平面ABCD,FC∥ED,且AB=ED=2FC=2,则异面直线AC与EF所成角的余弦值为
,多面体ABCDEF的体积为
.
三.解答题
15.(2021?浦东新区一模)如图,直三棱柱A1B1C1﹣ABC中,AB=AC=1,,A1A=4,点M为线段A1A的中点.
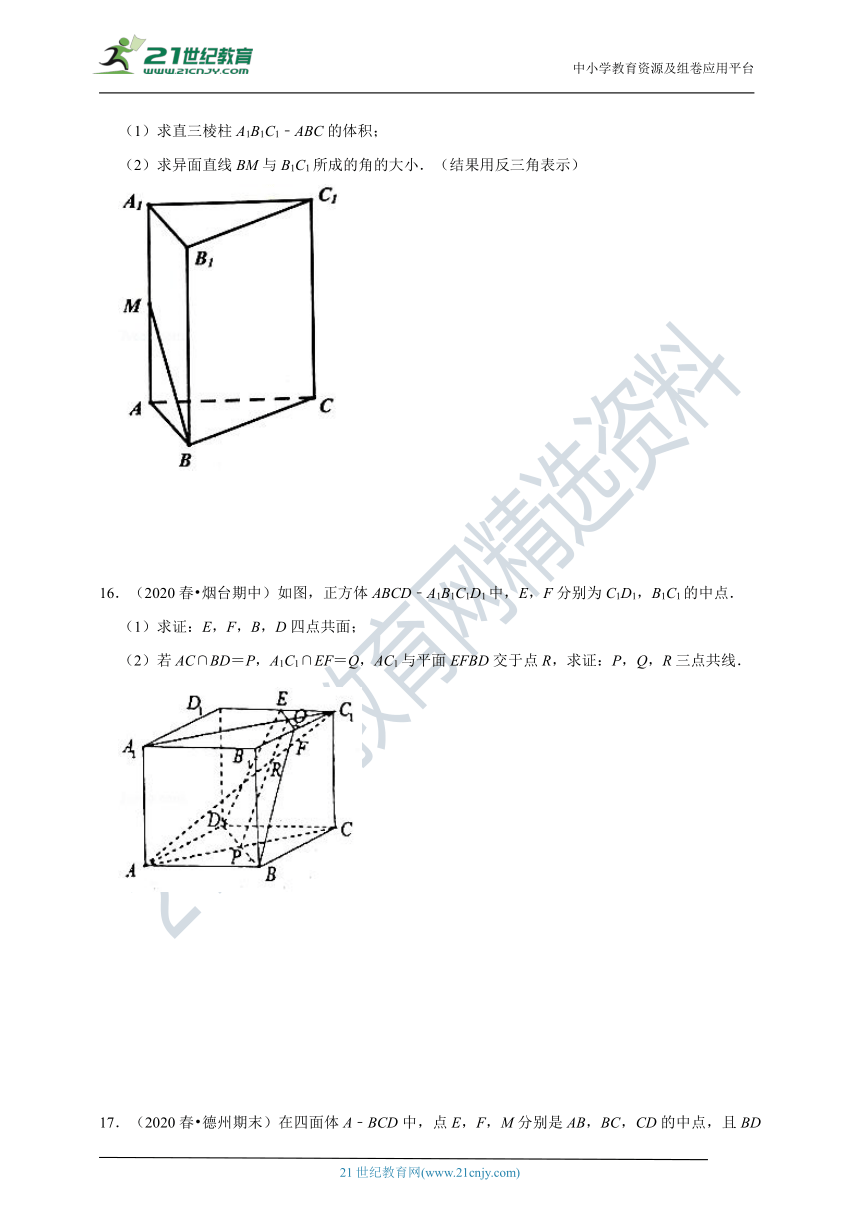
(1)求直三棱柱A1B1C1﹣ABC的体积;
(2)求异面直线BM与B1C1所成的角的大小.(结果用反三角表示)
16.(2020春?烟台期中)如图,正方体ABCD﹣A1B1C1D1中,E,F分别为C1D1,B1C1的中点.
(1)求证:E,F,B,D四点共面;
(2)若AC∩BD=P,A1C1∩EF=Q,AC1与平面EFBD交于点R,求证:P,Q,R三点共线.
17.(2020春?德州期末)在四面体A﹣BCD中,点E,F,M分别是AB,BC,CD的中点,且BD=AC=2,EM=1.
(1)求证:EF∥平面ACD;
(2)求异面直线AC与BD所成的角.
18.(2020?济南模拟)已知直角梯形ABCD中,AD∥BC,AB⊥BC,,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为的中点.
(1)求证:BM⊥DF;
(2)求异面直线BM与EF所成角的大小.
19.(2019秋?湖北期中)如图,四棱锥P﹣ABCD中,PA⊥CD,∠PAD=∠ABC=90°,AB∥CD,DC=CBAB=2,PA=2.
(1)求证:PA⊥平面ABCD;
(2)求异面直线AB与PD所成角的余弦值;
20.(2019秋?路南区校级期中)在直三棱柱ABC﹣A1B1C1中,AC=BC,∠ACB=90°,AA1=2,D为AB的中点.
(1)求异面直线AC1与B1C所成角的余弦值;
(2)在棱A1B1上是否存在一点M,使得平面C1AM∥平面B1CD.
21.(2020秋?河南月考)如图,在四棱锥P﹣ABCD中,AB∥CD,PD⊥CD,PD=2CD,过直线AB的平面与棱PC,PD分别交于点E,F.
(1)求异面直线PC与AB所成角的正切值;
(2)求证:EF∥CD.
参考答案与试题解析
一.选择题
1.【解答】解:以D为原点,DA、DC、DD1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
设正方体的棱长为2,则A(2,0,0),C(0,2,0),E(0,1,2),F(2,2,1),
∴(﹣2,1,2),(﹣2,0,﹣1),
∴cos,,
∴异面直线AE,FC所成的角的余弦值为.
故选:B.
2.【解答】解:设正方体的棱长为2,
以D为原点,DA,DC,DD1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则C(0,2,0),M(2,0,1),D1(0,0,2),N(2,2,1),
∴(2,﹣2,1),(2,2,﹣1),
∴cos,,
∵异面直线所成角的取值范围为(0,],
∴tan,,
∴CM与D1N所成角的正切值为.
故选:C.
3.【解答】解:由三个不同的平面α,β,γ,三条不重合的直线m,n,l,知:
在①中,若m⊥l,n⊥l,则m与n相交、平行或异面,故①错误;
在②中,若α⊥γ,β⊥γ,则α与β相交或平行,故②错误;
在③中,若m⊥α,m∥n,n?β,则由面面垂直的判断定理得α⊥β,故③正确;
在④中,若m∥α,α∩β=n,则m与n异面或平行,故④错误.
故选:A.
4.【解答】解:因为EF∥D1C1,
所以∠B1D1C1是异面直线B1D1与EF所成的角为45°,
故选项A正确,选项B错误;
在三棱锥D1﹣B1DC中,设点D1到平面DCB1的距离为h,
则有,
所以,
解得,
则直线B1D1与平面B1EF所成的角的正弦值为,
所以直线B1D1与平面B1EF所成的角为30°,
故选项C,D错误.
故选:A.
5.【解答】解:由三个不同的平面α,β,γ,三条不重合的直线m,n,l,知:
对于A,若m⊥l,n⊥l,则m与n相交、平行或异面,故A错误;
对于B,若a⊥γ,β⊥γ,则α与β平行或相交,故B错误;
对于C,若m⊥α,m∥n,n?β,则由面面垂直的判定定理得α⊥β,故C正确;
对于D,若m∥α,α∩β=n,则m与n平行或异面,故D错误.
故选:C.
6.【解答】解:∵在直棱柱ABC﹣A1B1C1中,AB⊥BC,
∴以B为原点,以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
∵AB=BC=BB1=2,点D是AC的中点,
∴A(0,2,0),B1(0,0,2),B(0,0,0),D(1,1,0),
(0,﹣2,2),(1,1,0),
设异面直线AB1与BD所成角的大小为θ,
则cosθ,
∴θ.
∴异面直线AB1与BD所成角的大小为.
故选:A.
7.【解答】解:因为l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,
若α∥β,则由线面垂直的判定定理得m⊥α,故选项A正确;
若α∥β,则由线面垂直的判定定理得m⊥α,
又l∥α,所以l⊥m,故选项B正确;
若l⊥m,则l与β平行或l?β,故选项C错误;
若m∥α,则由面面垂直的判定定理得α⊥β,故选项D正确.
故选:C.
二.填空题
8.【解答】解:由正四棱柱的性质知,AA1∥DD1,
∴∠DD1B即为异面直线AA1与BD1所成角,
在Rt△DD1B中,tan∠DD1B,
∴∠DD1B=arctan,
∴异面直线AA1与BD1所成角的大小是arctan.
故答案为:arctan.
9.【解答】解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
则A(0,0,0),B(4,0,0),C(4,4,0),E(0,0,2),
∴(﹣4,0,2),(4,4,0),
∴cos,,
∵异面直线夹角的取值范围为(0,],
∴异面直线BE与AC所成角的余弦值为.
故答案为:.
10.【解答】解:直线m∥平面α,直线n在α内,
所以直线m与n没有交点,
所以直线m与n所有可能的关系为平行或异面.
故答案为:平行或异面.
11.【解答】解:连接B1C,交BC1于点O,则O为BC1的中点,取AC的中点D,连接OD,
∴OD∥AB1,ODAB1,
∴∠BOD或其补角即为异面直线AB1与BC1所成角,
在△OBD中,BDAC,OBBC1,
由余弦定理知,cos∠BOD,
∴sin∠BOD,
∴异面直线AB1与BC1所成角的正弦值为.
故答案为:.
12.【解答】解:如图所示,
∵E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
∴EFAC,HGAC,
∴EFHG,
∴四边形EFGH是平行四边形.
又AC⊥BD,
∴EF⊥EH.
则四边形EFGH的形状是矩形.
故答案为:矩形.
13.【解答】解:正方体共有8个顶点,若选出的k条线两两异面,则不能共顶点,即至多可选出4条,
又可以选出4条两两异面的线(如图DB,B1C,A1C1,AD1),故所求k的最大值是4.
故答案为:4.
14.【解答】解:取DE的中点G,连接GA,GC,BD,则有CF∥EG,CFDE=EG,
∴四边形CGEF为平行四边形,∴EF∥CG,
∴∠ACG或其补角为异面直线AC与EF所成的角.
由勾股定理可知,CG=AG,AC,
在等腰△ACG中,cos∠ACG,
∴异面直线AC与EF所成角的余弦值为.
∵DE⊥平面ABCD,∴DE⊥BC,
∵BC⊥CD,DE∩CD=C,DE、CD?平面CDEF,
∴BC⊥平面CDEF,
∴VB﹣CDEFBC?S梯形CDEF22=2,
VE﹣ABDDE?S△ABD22×2,
∴多面体ABCDEF的体积V=VB﹣CDEF+VE﹣ABD=2.
故答案为:;.
三.解答题
15.【解答】解:(1)∵,
∴V=S△ABC?A1A4=2.
(2)∵BC∥B1C1,
∴∠MBC或其补角是异面直线BM与B1C1所成的角,
在△MBC中,BM=CM,BC,
由余弦定理得,cos∠MBC,
∴∠MBC=arccos,
故异面直线BM与B1C1所成的角为.
16.【解答】证明:(1)连接B1D1,
在正方体ABCD﹣A1B1C1D1中,∵E,F分别为C1D1,B1C1的中点,
∴EF是△B1C1D1的中位线,∴EF∥B1D1,
又因为B1D1∥BD,∴EF∥BD
∴四边形BDEF为梯形,即B,D,E,F四点共面.
(2)在正方体ABCD﹣A1B1C1D1中,AC∩BD=P,A1C1∩EF=Q,
∴PQ是平面AA1C1C与平面BDEF的交线,
又因为AC1交平面BDEF于点R,
∴R是平面AA1C1C与平面BDEF的一个公共点.
因为两平面相交的所有公共点都在这两个平面的交线上,
∴P,Q,R三点共线.
17.【解答】解:(1)证明:∵点E,F分别是AB,BC的中点,∴EF∥AC,
∵EF?平面ACD,AC?平面ACD,
∴EF∥平面ACD.
(2)解:∵点E,F,M分别是AB,BC,CD的中点,
∴EF∥AC,FM∥BD,
∴∠EFM是异面直线AC与BD所成的角(或所成角的补角),
在△EFM中,EF=FM=EM=1,
∴△EFM是等边三角形,∴∠EFM=60°,
∴异面直线AC与BD所成的角为60°.
18.【解答】(1)证明:∵AB⊥BC,AB⊥BE,BC∩BE=B,
∴AB⊥平面BCE,
以B为原点,以BE,BC,BA为坐标轴建立空间坐标系B﹣xyz,如图所示:
设AB=AD=1,则D(0,1,1),F(1,0,1),B(0,0,0),M(,,0),
∴(,,0),(1,﹣1,0),
∴0=0,
∴BM⊥DF.
(2)解:E(2,0,0),故(﹣1,0,1),
∴cos,,
∴设异面直线BM与EF所成角为θ,则cosθ=|cos,|,
故θ.
19.【解答】(1)证明:∵PA⊥CD,PA⊥AD,CD∩AD=D,
∴PA⊥平面ABCD,
(2)∵AB∥CD,
∴∠PDC为异面直线AB与PD所成的角或其补角,
∵PA⊥平面ABCD,
∴在Rt△PAD中,,,
∴,
∴,
∴异面直线AB与PD所成角的余弦值为:.
20.【解答】解:(1)以C为原点,CB、CA、CC1分别为x、z、y轴建立空间直角坐标系.
因为AC=BC,AA1=2.
所以C(0,0,0),A(),C1(0,2,0),.
所以,
那么;
(2)在A1B1上中点M,连接MA.
证明如下:
∵三棱柱ABC﹣A1B1C1是直三棱.
∴平面ABC∥平面A1B1C1,AB∥A1B1,AB=A1B1.
∵D、M分别是AB、A1B1的中点.
∴C1M∥CD.
∵CD?平面CDB1,C1M?平面CDB1,
∴C1M∥平面CDB1.
∴,.
∴MB1=AD,MB1∥AD.
∴四边形ADB1M是平行四边形.
∴AM∥DB1.
∵DB1?平面DCB1,AM?平面DBC1.
∴AM∥平面DCB1.
∵C1M∩AM=M.
∴平面C1AM∥平面B1CD.
21.【解答】(1)解:∵AB∥CD,∴∠PCD即为异面直线PC与AB所成的角或其补角.
∵PD⊥CD,PD=2CD,∴,
又∠PCD∈(0°,90°],∴异面直线PC与AB所成角的正切值为2.
(2)证明:∵AB∥CD,
又CD?平面PCD,AB?平面PCD,∴AB∥平面PCD.
又由题意,得平面ABEF∩平面PCD=EF,AB?平面ABEF,
∴AB∥EF,∴EF∥CD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题基础练
第二章《点、直线、平面之间的位置关系》
2.1
空间点、直线、平面之间的位置关系
一.选择题
1.(2021?二模拟)正方体ABCD﹣A1B1C1D1中,E,F分别为D1C1,BB1的中点,则异面直线AE,FC所成的角的余弦值为( )
A.
B.
C.
D.
2.(2021?五模拟)在正方体ABCD﹣A1B1C1D1中,M,N分别为棱AA1和BB1的中点,则CM与D1N所成角的正切值为( )
A.
B.
C.4
D.﹣4
3.(2020秋?香坊区校级期末)已知三个不同的平面α,β,γ,三条不重合的直线m,n,l,有下列四个命题:
①若m⊥l,n⊥l,则m∥n;
②若α⊥γ,β⊥γ,则α∥β;
③若m⊥α,m∥n,n?β,则α⊥β;
④若m∥α,α∩β=n,则m∥n
其中真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
4.(2020秋?皇姑区校级期末)如图所示,设E、F分别是正方体ABCD﹣A1B1C1D1的棱CD上两点,且AB=2,EF=1,其中正确的命题为( )
A.异面直线B1D1与EF所成的角为45°
B.异面直线B1D1与EF所成的角为30°
C.直线B1D1与平面B1EF所成的角为45°
D.直线B1D1与平面B1EF所成的角为60°
5.(2020秋?香坊区校级期末)已知三个不同的平面α,β,γ,三条不重合的直线m,n,l,有下列四个命题中正确的是( )
A.若m⊥l,n⊥l,则m∥n
B.若a⊥γ,β⊥γ,则α∥β
C.若m⊥α,m∥n,n?β,则α⊥β
D.若m∥α,α∩β=n,则m∥n
6.(2020秋?朝阳区校级期末)在直棱柱ABC﹣A1B1C1中,AB⊥BC,其中AB=BC=BB1=2,点D是AC的中点,则异面直线AB1与BD所成角的大小为( )
A.
B.
C.
D.
7.(2020秋?城关区校级期末)已知l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,则下列命题中不正确的是( )
A.若α∥β,则m⊥α
B.若α∥β,则l⊥m
C.若l⊥m,则l∥β
D.若m∥α,则α⊥β
二.填空题
8.(2021?闵行区一模)如图,已知正四棱柱ABCD﹣A1B1C1D1的底面边长为2,高为3,则异面直线AA1与BD1所成角的大小是
.
9.(2020秋?宝应县月考)四棱锥P﹣ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=4,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是
.
10.(2020秋?秦都区校级月考)已知直线m∥平面α,直线n在α内,则m与n所有可能的位置关系是
.
11.(2020秋?海曙区校级期中)已知直三棱柱ABC﹣A1B1C1中,∠ABC=90°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的正弦值为
.
12.(2020秋?闵行区校级期末)设E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,若AC⊥BD,则四边形EFGH的形状是
.
13.(2020秋?闵行区校级期末)在所有经过正方体ABCD﹣A1B1C1D1的任意两个顶点的直线中任取k条,求这k条直线恰是两两异面,则k的最大值为
.
14.(2021?十三模拟)如图,在多面体ABCDEF中,四边形ABCD为正方形,ED⊥平面ABCD,FC∥ED,且AB=ED=2FC=2,则异面直线AC与EF所成角的余弦值为
,多面体ABCDEF的体积为
.
三.解答题
15.(2021?浦东新区一模)如图,直三棱柱A1B1C1﹣ABC中,AB=AC=1,,A1A=4,点M为线段A1A的中点.
(1)求直三棱柱A1B1C1﹣ABC的体积;
(2)求异面直线BM与B1C1所成的角的大小.(结果用反三角表示)
16.(2020春?烟台期中)如图,正方体ABCD﹣A1B1C1D1中,E,F分别为C1D1,B1C1的中点.
(1)求证:E,F,B,D四点共面;
(2)若AC∩BD=P,A1C1∩EF=Q,AC1与平面EFBD交于点R,求证:P,Q,R三点共线.
17.(2020春?德州期末)在四面体A﹣BCD中,点E,F,M分别是AB,BC,CD的中点,且BD=AC=2,EM=1.
(1)求证:EF∥平面ACD;
(2)求异面直线AC与BD所成的角.
18.(2020?济南模拟)已知直角梯形ABCD中,AD∥BC,AB⊥BC,,将直角梯形ABCD(及其内部)以AB所在直线为轴顺时针旋转90°,形成如图所示的几何体,其中M为的中点.
(1)求证:BM⊥DF;
(2)求异面直线BM与EF所成角的大小.
19.(2019秋?湖北期中)如图,四棱锥P﹣ABCD中,PA⊥CD,∠PAD=∠ABC=90°,AB∥CD,DC=CBAB=2,PA=2.
(1)求证:PA⊥平面ABCD;
(2)求异面直线AB与PD所成角的余弦值;
20.(2019秋?路南区校级期中)在直三棱柱ABC﹣A1B1C1中,AC=BC,∠ACB=90°,AA1=2,D为AB的中点.
(1)求异面直线AC1与B1C所成角的余弦值;
(2)在棱A1B1上是否存在一点M,使得平面C1AM∥平面B1CD.
21.(2020秋?河南月考)如图,在四棱锥P﹣ABCD中,AB∥CD,PD⊥CD,PD=2CD,过直线AB的平面与棱PC,PD分别交于点E,F.
(1)求异面直线PC与AB所成角的正切值;
(2)求证:EF∥CD.
参考答案与试题解析
一.选择题
1.【解答】解:以D为原点,DA、DC、DD1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
设正方体的棱长为2,则A(2,0,0),C(0,2,0),E(0,1,2),F(2,2,1),
∴(﹣2,1,2),(﹣2,0,﹣1),
∴cos,,
∴异面直线AE,FC所成的角的余弦值为.
故选:B.
2.【解答】解:设正方体的棱长为2,
以D为原点,DA,DC,DD1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则C(0,2,0),M(2,0,1),D1(0,0,2),N(2,2,1),
∴(2,﹣2,1),(2,2,﹣1),
∴cos,,
∵异面直线所成角的取值范围为(0,],
∴tan,,
∴CM与D1N所成角的正切值为.
故选:C.
3.【解答】解:由三个不同的平面α,β,γ,三条不重合的直线m,n,l,知:
在①中,若m⊥l,n⊥l,则m与n相交、平行或异面,故①错误;
在②中,若α⊥γ,β⊥γ,则α与β相交或平行,故②错误;
在③中,若m⊥α,m∥n,n?β,则由面面垂直的判断定理得α⊥β,故③正确;
在④中,若m∥α,α∩β=n,则m与n异面或平行,故④错误.
故选:A.
4.【解答】解:因为EF∥D1C1,
所以∠B1D1C1是异面直线B1D1与EF所成的角为45°,
故选项A正确,选项B错误;
在三棱锥D1﹣B1DC中,设点D1到平面DCB1的距离为h,
则有,
所以,
解得,
则直线B1D1与平面B1EF所成的角的正弦值为,
所以直线B1D1与平面B1EF所成的角为30°,
故选项C,D错误.
故选:A.
5.【解答】解:由三个不同的平面α,β,γ,三条不重合的直线m,n,l,知:
对于A,若m⊥l,n⊥l,则m与n相交、平行或异面,故A错误;
对于B,若a⊥γ,β⊥γ,则α与β平行或相交,故B错误;
对于C,若m⊥α,m∥n,n?β,则由面面垂直的判定定理得α⊥β,故C正确;
对于D,若m∥α,α∩β=n,则m与n平行或异面,故D错误.
故选:C.
6.【解答】解:∵在直棱柱ABC﹣A1B1C1中,AB⊥BC,
∴以B为原点,以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
∵AB=BC=BB1=2,点D是AC的中点,
∴A(0,2,0),B1(0,0,2),B(0,0,0),D(1,1,0),
(0,﹣2,2),(1,1,0),
设异面直线AB1与BD所成角的大小为θ,
则cosθ,
∴θ.
∴异面直线AB1与BD所成角的大小为.
故选:A.
7.【解答】解:因为l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,
若α∥β,则由线面垂直的判定定理得m⊥α,故选项A正确;
若α∥β,则由线面垂直的判定定理得m⊥α,
又l∥α,所以l⊥m,故选项B正确;
若l⊥m,则l与β平行或l?β,故选项C错误;
若m∥α,则由面面垂直的判定定理得α⊥β,故选项D正确.
故选:C.
二.填空题
8.【解答】解:由正四棱柱的性质知,AA1∥DD1,
∴∠DD1B即为异面直线AA1与BD1所成角,
在Rt△DD1B中,tan∠DD1B,
∴∠DD1B=arctan,
∴异面直线AA1与BD1所成角的大小是arctan.
故答案为:arctan.
9.【解答】解:以A为原点,AB,AD,AP所在的直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
则A(0,0,0),B(4,0,0),C(4,4,0),E(0,0,2),
∴(﹣4,0,2),(4,4,0),
∴cos,,
∵异面直线夹角的取值范围为(0,],
∴异面直线BE与AC所成角的余弦值为.
故答案为:.
10.【解答】解:直线m∥平面α,直线n在α内,
所以直线m与n没有交点,
所以直线m与n所有可能的关系为平行或异面.
故答案为:平行或异面.
11.【解答】解:连接B1C,交BC1于点O,则O为BC1的中点,取AC的中点D,连接OD,
∴OD∥AB1,ODAB1,
∴∠BOD或其补角即为异面直线AB1与BC1所成角,
在△OBD中,BDAC,OBBC1,
由余弦定理知,cos∠BOD,
∴sin∠BOD,
∴异面直线AB1与BC1所成角的正弦值为.
故答案为:.
12.【解答】解:如图所示,
∵E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,
∴EFAC,HGAC,
∴EFHG,
∴四边形EFGH是平行四边形.
又AC⊥BD,
∴EF⊥EH.
则四边形EFGH的形状是矩形.
故答案为:矩形.
13.【解答】解:正方体共有8个顶点,若选出的k条线两两异面,则不能共顶点,即至多可选出4条,
又可以选出4条两两异面的线(如图DB,B1C,A1C1,AD1),故所求k的最大值是4.
故答案为:4.
14.【解答】解:取DE的中点G,连接GA,GC,BD,则有CF∥EG,CFDE=EG,
∴四边形CGEF为平行四边形,∴EF∥CG,
∴∠ACG或其补角为异面直线AC与EF所成的角.
由勾股定理可知,CG=AG,AC,
在等腰△ACG中,cos∠ACG,
∴异面直线AC与EF所成角的余弦值为.
∵DE⊥平面ABCD,∴DE⊥BC,
∵BC⊥CD,DE∩CD=C,DE、CD?平面CDEF,
∴BC⊥平面CDEF,
∴VB﹣CDEFBC?S梯形CDEF22=2,
VE﹣ABDDE?S△ABD22×2,
∴多面体ABCDEF的体积V=VB﹣CDEF+VE﹣ABD=2.
故答案为:;.
三.解答题
15.【解答】解:(1)∵,
∴V=S△ABC?A1A4=2.
(2)∵BC∥B1C1,
∴∠MBC或其补角是异面直线BM与B1C1所成的角,
在△MBC中,BM=CM,BC,
由余弦定理得,cos∠MBC,
∴∠MBC=arccos,
故异面直线BM与B1C1所成的角为.
16.【解答】证明:(1)连接B1D1,
在正方体ABCD﹣A1B1C1D1中,∵E,F分别为C1D1,B1C1的中点,
∴EF是△B1C1D1的中位线,∴EF∥B1D1,
又因为B1D1∥BD,∴EF∥BD
∴四边形BDEF为梯形,即B,D,E,F四点共面.
(2)在正方体ABCD﹣A1B1C1D1中,AC∩BD=P,A1C1∩EF=Q,
∴PQ是平面AA1C1C与平面BDEF的交线,
又因为AC1交平面BDEF于点R,
∴R是平面AA1C1C与平面BDEF的一个公共点.
因为两平面相交的所有公共点都在这两个平面的交线上,
∴P,Q,R三点共线.
17.【解答】解:(1)证明:∵点E,F分别是AB,BC的中点,∴EF∥AC,
∵EF?平面ACD,AC?平面ACD,
∴EF∥平面ACD.
(2)解:∵点E,F,M分别是AB,BC,CD的中点,
∴EF∥AC,FM∥BD,
∴∠EFM是异面直线AC与BD所成的角(或所成角的补角),
在△EFM中,EF=FM=EM=1,
∴△EFM是等边三角形,∴∠EFM=60°,
∴异面直线AC与BD所成的角为60°.
18.【解答】(1)证明:∵AB⊥BC,AB⊥BE,BC∩BE=B,
∴AB⊥平面BCE,
以B为原点,以BE,BC,BA为坐标轴建立空间坐标系B﹣xyz,如图所示:
设AB=AD=1,则D(0,1,1),F(1,0,1),B(0,0,0),M(,,0),
∴(,,0),(1,﹣1,0),
∴0=0,
∴BM⊥DF.
(2)解:E(2,0,0),故(﹣1,0,1),
∴cos,,
∴设异面直线BM与EF所成角为θ,则cosθ=|cos,|,
故θ.
19.【解答】(1)证明:∵PA⊥CD,PA⊥AD,CD∩AD=D,
∴PA⊥平面ABCD,
(2)∵AB∥CD,
∴∠PDC为异面直线AB与PD所成的角或其补角,
∵PA⊥平面ABCD,
∴在Rt△PAD中,,,
∴,
∴,
∴异面直线AB与PD所成角的余弦值为:.
20.【解答】解:(1)以C为原点,CB、CA、CC1分别为x、z、y轴建立空间直角坐标系.
因为AC=BC,AA1=2.
所以C(0,0,0),A(),C1(0,2,0),.
所以,
那么;
(2)在A1B1上中点M,连接MA.
证明如下:
∵三棱柱ABC﹣A1B1C1是直三棱.
∴平面ABC∥平面A1B1C1,AB∥A1B1,AB=A1B1.
∵D、M分别是AB、A1B1的中点.
∴C1M∥CD.
∵CD?平面CDB1,C1M?平面CDB1,
∴C1M∥平面CDB1.
∴,.
∴MB1=AD,MB1∥AD.
∴四边形ADB1M是平行四边形.
∴AM∥DB1.
∵DB1?平面DCB1,AM?平面DBC1.
∴AM∥平面DCB1.
∵C1M∩AM=M.
∴平面C1AM∥平面B1CD.
21.【解答】(1)解:∵AB∥CD,∴∠PCD即为异面直线PC与AB所成的角或其补角.
∵PD⊥CD,PD=2CD,∴,
又∠PCD∈(0°,90°],∴异面直线PC与AB所成角的正切值为2.
(2)证明:∵AB∥CD,
又CD?平面PCD,AB?平面PCD,∴AB∥平面PCD.
又由题意,得平面ABEF∩平面PCD=EF,AB?平面ABEF,
∴AB∥EF,∴EF∥CD.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
