【同步必刷题】2.1 空间点、直线、平面之间的位置关系 提高练(含解析)
文档属性
| 名称 | 【同步必刷题】2.1 空间点、直线、平面之间的位置关系 提高练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:13:09 | ||
图片预览


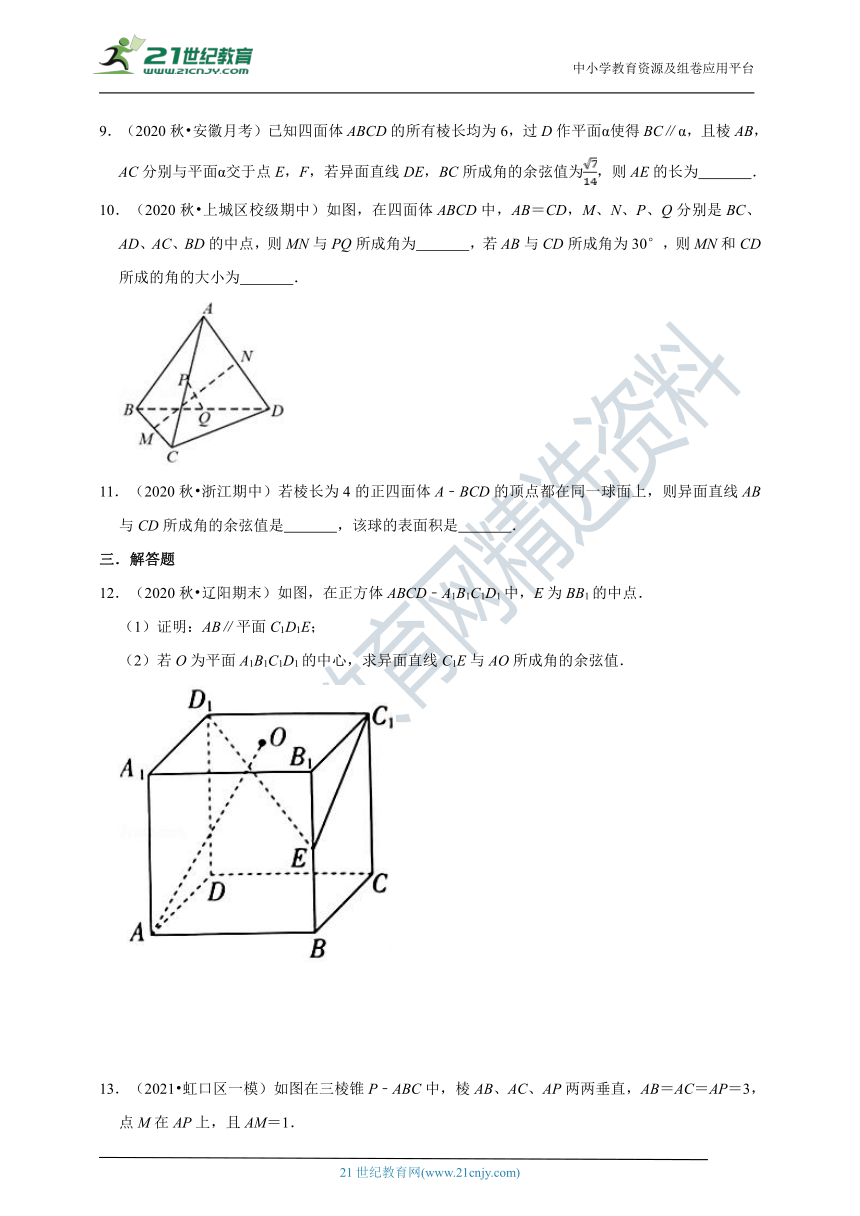

文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题提高练
第二章《点、直线、平面之间的位置关系》
2.1
空间点、直线、平面之间的位置关系
一.选择题
1.(2020秋?河南月考)设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
A.若α∥β,m?α,n?β,则m∥n
B.若α⊥β,m?α,n?β,则m⊥n
C.若点A,B到α平面的距离相等,则直线AB∥α
D.若m⊥α,m∥β,则α⊥β
2.(2020秋?朝阳区校级期末)在直棱柱ABC﹣A1B1C1中,AB⊥BC,其中AB=BC=BB1=2,点D是AC的中点,则异面直线AB1与BD所成角的大小为( )
A.
B.
C.
D.
3.(2020秋?城关区校级期末)已知l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,则下列命题中不正确的是( )
A.若α∥β,则m⊥α
B.若α∥β,则l⊥m
C.若l⊥m,则l∥β
D.若m∥α,则α⊥β
4.(2020秋?长安区校级期末)在三棱锥P﹣ABC中,PA,PB,PC两两垂直,且PA=PB=PC,M,N分别为AC,AB的中点,则异面直线PN和BM所成角的余弦值为( )
A.
B.
C.
D.
二.填空题
5.(2021?浙江模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为6,点F是棱AA1的中点,AC与BD的交点为O,点M在棱BC上,且BM=2MC,动点T(不同于点M)在四边形ABCD内部及其边界上运动,且TM⊥OF,则直线B1F与TM所成角的余弦值为
.
6.(2020秋?汾阳市期中)如图,在正方体中,A,B,C,D分别是顶点或所在棱的中点,则A,B,C,D四点共面的图形有
(填上所有正确答案的序号).
7.(2020秋?南海区校级月考)如图,在三棱锥A﹣BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则:
(1)当AC,BD满足条件
时,四边形EFGH为菱形;
(2)当AC,BD满足条件
时,四边形EFGH为正方形.
8.(2020秋?河南月考)若正三棱锥A﹣BCD的侧棱长为8,底面边长为4,E,F分别为AC,AD上的动点(如图),则截面△BEF的周长最小值为
.
9.(2020秋?安徽月考)已知四面体ABCD的所有棱长均为6,过D作平面α使得BC∥α,且棱AB,AC分别与平面α交于点E,F,若异面直线DE,BC所成角的余弦值为,则AE的长为
.
10.(2020秋?上城区校级期中)如图,在四面体ABCD中,AB=CD,M、N、P、Q分别是BC、AD、AC、BD的中点,则MN与PQ所成角为
,若AB与CD所成角为30°,则MN和CD所成的角的大小为
.
11.(2020秋?浙江期中)若棱长为4的正四面体A﹣BCD的顶点都在同一球面上,则异面直线AB与CD所成角的余弦值是
,该球的表面积是
.
三.解答题
12.(2020秋?辽阳期末)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(1)证明:AB∥平面C1D1E;
(2)若O为平面A1B1C1D1的中心,求异面直线C1E与AO所成角的余弦值.
13.(2021?虹口区一模)如图在三棱锥P﹣ABC中,棱AB、AC、AP两两垂直,AB=AC=AP=3,点M在AP上,且AM=1.
(1)求异面直线BM和PC所成的角的大小;
(2)求三棱锥P﹣BMC的体积.
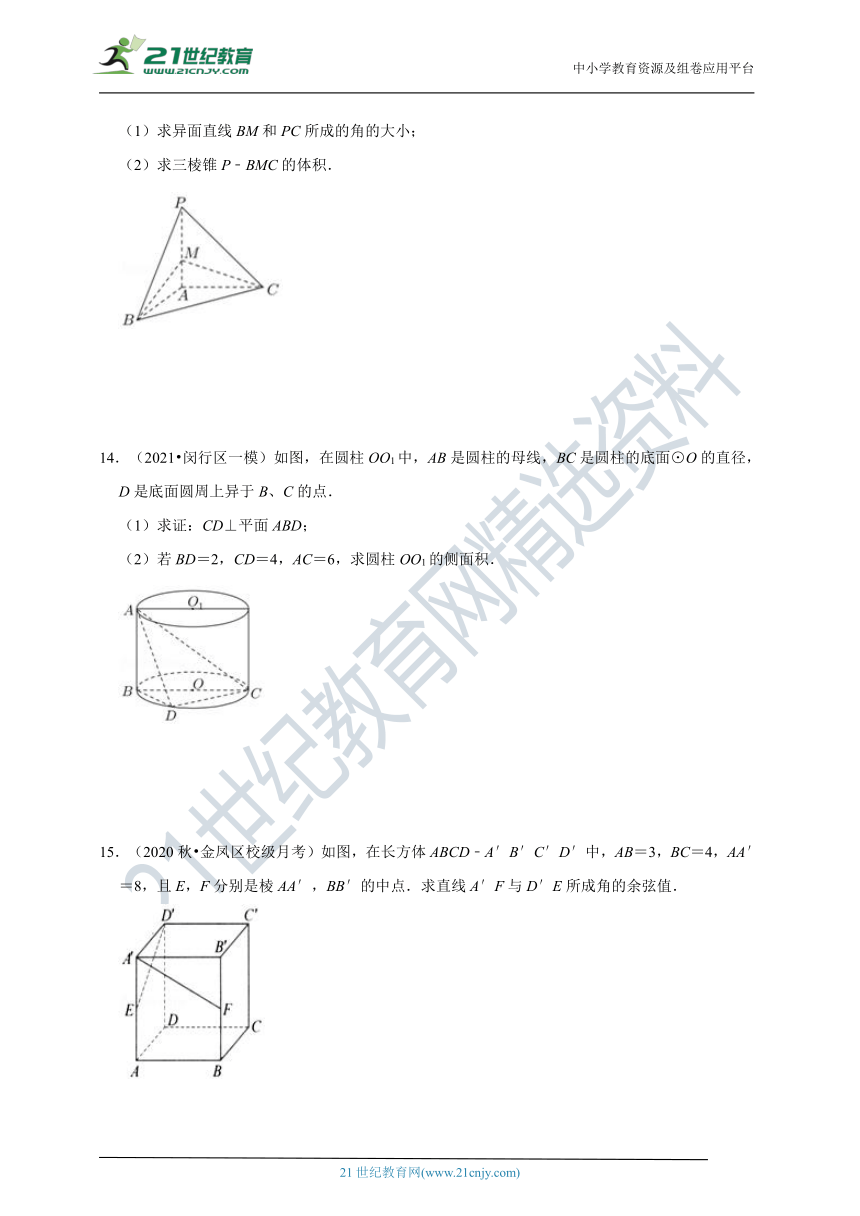
14.(2021?闵行区一模)如图,在圆柱OO1中,AB是圆柱的母线,BC是圆柱的底面⊙O的直径,D是底面圆周上异于B、C的点.
(1)求证:CD⊥平面ABD;
(2)若BD=2,CD=4,AC=6,求圆柱OO1的侧面积.
15.(2020秋?金凤区校级月考)如图,在长方体ABCD﹣A′B′C′D′中,AB=3,BC=4,AA′=8,且E,F分别是棱AA′,BB′的中点.求直线A′F与D′E所成角的余弦值.
16.(2020秋?南岗区校级期末)已知正四棱锥S﹣ABCD的侧棱长为,底面的边长为,E是SA的中点,求异面直线BE与SC所成的角.
17.(2020秋?重庆期末)已知圆台O1O2,轴截面ABCD,圆台的上底面圆半径与高相等,下底面圆半径为高的两倍,点E为下底圆弧的中点,点N为上底圆周上靠近点A的的四等分点,经过O1,O2,N三点的平面与弧交于点M,且E,M,N三点在平面ABCD的同侧.
(Ⅰ)判断平面O1O2MN与直线CE的位置关系,并证明你的结论;
(Ⅱ)P为上底圆周上的一个动点,当四棱锥P﹣ABCD的体积最大时,求异面直线CP与DB所成角的余弦值.
18.(2021?嘉定区一模)如图,正四棱柱ABCD﹣A1B1C1D1的底面边长为2,A1D=4.
(1)求该正四棱柱的表面积和体积;
(2)求异面直线A1D与AC所成的角的大小(结果用反三角函数值表示).
19.(2021?徐汇区一模)如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=2,CC1=4,∠ACB=90°,E、F分别为棱AA1、AB的中点.
(1)求异面直线A1C与EF所成的角的大小(结果用反三角函数值表示);
(2)求五棱锥C﹣EFBB1A1的体积.
20.(2020秋?黄浦区校级月考)空间四边形ABCD中,AB=CD,点M、N分别为对角线BD、AC的中点.
(1)若直线AB与MN所成角为60°,求直线AB与CD所成角的大小;
(2)若直线AB与CD所成角为θ,求直线AB与MN所成角的大小.
21.(2020秋?河南月考)如图所示,三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
(1)当点M在何位置时,BM∥平面AEF?
(2)若BM∥平面AEF,判断BM与EF的位置关系,说明理由;并求BM与EF所成的角的余弦值.
22.(2020秋?聊城期中)如图所示,已知空间四边形ABCD的每条边和对角线都等于1,点E,F分别是AB,AD的中点,设,,为空间向量的一组基底,,,,试用基底向量法求解以下各题.求:
(1);
(2)求异面直线CF与BD所成角的余弦值.
参考答案与试题解析
一.选择题
1.【解答】解:由α∥β,m?α,n?β,得m∥n或m与n异面,故A错误;
若α⊥β,m?α,n?β,则m∥n或m与n相交或m与n异面,相交或异面时也不一定垂直,故B错误;
若点A,B到α平面的距离相等,AB可能与α平行,也可能与平面a相交,故C错误;
若m∥β,过m作平面与β相交,交线为n,则m∥n,又m⊥α,所以n⊥α,得α⊥β,故D正确.
故选:D.
2.【解答】解:∵在直棱柱ABC﹣A1B1C1中,AB⊥BC,
∴以B为原点,以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
∵AB=BC=BB1=2,点D是AC的中点,
∴A(0,2,0),B1(0,0,2),B(0,0,0),D(1,1,0),
(0,﹣2,2),(1,1,0),
设异面直线AB1与BD所成角的大小为θ,
则cosθ,
∴θ.
∴异面直线AB1与BD所成角的大小为.
故选:A.
3.【解答】解:因为l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,
若α∥β,则由线面垂直的判定定理得m⊥α,故选项A正确;
若α∥β,则由线面垂直的判定定理得m⊥α,
又l∥α,所以l⊥m,故选项B正确;
若l⊥m,则l与β平行或l?β,故选项C错误;
若m∥α,则由面面垂直的判定定理得α⊥β,故选项D正确.
故选:C.
4.【解答】解:∵在三棱锥P﹣ABC中,PA,PB,PC两两垂直,且PA=PB=PC,M,N分别为AC,AB的中点,
∴以P为原点,PA为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,
设PA=PB=PC=2,则P(0,0,0),N(1,1,0),B(0,2,0),M(1,0,1),
(1,1,0),(1,﹣2,1),
设异面直线PN和BM所成角为θ,
则cosθ.
∴异面直线PN和BM所成角的余弦值为.
故选:D.
二.填空题
5.【解答】解:以A为原点,AD,AB,AA1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则B1(0,6,6),F(0,0,3),M(4,6,0),O(3,3,0),
设T(x,y,0),则(4﹣x,6﹣y,0),(0,﹣6,﹣3),(﹣3,﹣3,3),
∵TM⊥OF,
∴?0,即﹣3(4﹣x)﹣3(6﹣y)=0,
∴y=10﹣x,
∴(4﹣x,x﹣4,0),
∴|cos,|=||=||=||,
∵点T与点M不重合,∴x﹣4≠0,∴|cos,|,
∴直线B1F与TM所成角的余弦值为.
故答案为:.
6.【解答】解:如图所示:
对于①作中点F,
所以EF∥CD∥AB,则A、B、C、D四点共面.
对于②直线AB和CD
为异面直线,
对于③:如图所示:
连接EF,所以AC∥EF∥BD,
故A、B、C、D四点共面,
对于④:如图所示:
连接EF,GH,
所以AC∥BD∥EF∥GH,
故A、B、C、D四点共面,
对于⑤:直线AB和CD
为异面直线,
故答案为:①③④.
7.【解答】解:(1)因为四边形
EFGH
为菱形,所以
EF=EH,所以
AC=BD.
解:(2)因为四边形
EFGH
为正方形,
所以
EF=EH
且
EF⊥EH,
因为
EF∥AC,EH∥BD,且
,,
所以
AC=BD
且
AC⊥BD.
8.【解答】解:正三棱锥A﹣BCD的侧面展开图如图,
由平面几何知识可得BB'∥CD,
所以∠BEC=∠ECD=∠ACB,
于是△BCE∽△ABC,
所以.
即,
所以CE=2,
所以AE=6,
又,
可得EF=3.
截面△BEF的周长最小值为:4+3+4=11.
故答案为:11.
9.【解答】解:由题意可得EF∥BC,异面直线DE,BC所成的角为∠DEF,且cos∠DEF,
设AE=EF=x(0<x<6),则DE=DF,
于是cos∠DEF,
解得x=2,
即AE的长为2.
故答案为:2.
10.【解答】解:连接MP,NP,MQ,NQ,
∵M、N、P、Q分别为BC、AD、AC、BD的中点,
∴MQ∥CD,MQCD,NP∥CD,NPCD,
∴MQ∥NP,MQ=NP,
∴四边形MPNQ是平行四边形,
∵MPAB,AB=CD,∴MPCD,
∴MP=MQ,
∴平行四边形MPNQ是菱形,
∴MN⊥PQ,
∴MN与PQ所成角为90°.
∵MP∥AB,MQ∥CD,
∴∠PMQ或其补角即为AB与CD所成的角,
∴∠PMQ=30°或150°,
∵MQ∥CD,
∴∠NMQ为MN和CD所成角,
而∠NMQ∠PMQ=15°或75°,
∴MN和CD所成角为15°或75°.
故答案为:90°;15°或75°.
11.【解答】解:取CD中点E,连接BE、AE,
∵棱长为4的正四面体A﹣BCD中,BC=BD,AC=AD,
∴BE⊥CD,AE⊥CD,
∵BE∩AE=E,∴CD⊥平面ABE,
∵AB?平面ABE,∴AB⊥CD,
∴异面直线AB与CD所成角的余弦值是cos0.
过A作AF⊥平面BCD,交BE于F,
棱长为4的正四面体A﹣BCD的顶点都在同一球面上,则球心O在AF上,连结OB,
设球半径为R,
BE2,BF,AF,
∵OB=OA=R,∴OF,
∵OB2=BF2+OF2,∴R2=()2+()2,
解得R,
∴该球的表面积是S=4πR2=4π×6=24π.
故答案为:0,24π.
三.解答题
12.【解答】解:(1)证明:∵在正方体ABCD﹣A1B1C1D1中,AB∥CD∥C1D1,
∴AB∥C1D1,
∵AB?平面C1D1E,C1D1?平面C1D1E,
∴AB∥平面C1D1E.
(2)以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AB=2,则A(2,0,0),O(1,1,2),C1(0,2,2),E(2,2,1),
∵(2,0,﹣1),(﹣1,1,2),
∴cos,
∴异面直线C1E与AO所成角的余弦值为.
13.【解答】解:(1)在AC上取点N,使ANAC=1,连接MN,BN,
∵AP=3,AM=1,
∴MN∥PC,
∴∠BMN或其补角即为异面直线BM和PC所成的角,
在△BMN中,BM,MN,BN,
由余弦定理知,cos∠BMN,
∴∠BMN=arccos,
∴异面直线BM和PC所成的角的大小为arccos.
(2)V=VP﹣ABC﹣VM﹣ABCS△ABC?(AP﹣AM)3×3×2=3,
故三棱锥P﹣BMC的体积为3.
14.【解答】证明:(1)∵AB⊥底面BCD,∴AB⊥CD,
又CD⊥BD,且AB∩BD=B,
∴CD⊥平面ABD;
解:(2)在Rt△BCD中,由BD=2,CD=4,
得BC,
又在Rt△ABC中,AC=6,得AB.
∴圆柱的底面半径为,母线长为4,
∴圆柱OO1的侧面积为.
15.【解答】解:连接C′F,A′C′,因为E,F分别是棱AA′,BB′的中点.
所以D′E∥C′F,所以直线A′F与D′E所成的角为∠A′FC′或其补角,
在长方体ABCD﹣A′B′C′D′中,AB=3,BC=4,AA′=8,
所以B′F=4,则A′F=5,C′F=4,A′C′=5,
所以cos∠A′FC′,
即直线A′F与D′E所成角的余弦值为.
16.【解答】解:连接底面正方形ABCD对角线AC、BD,交于F,
则F是AC和BD的中点,
连接EF,BD,EF是三角形ASC的中位线,EF∥SC,
且EFSC,则∠BEF或补角即为BE与SC的所成角,
BF,AB,EF,
三角形SAB是等腰三角形,从S作SG⊥AB,
cos∠SAB,
根据余弦定理,BE2=AE2+AB2﹣2AE?AB?cos∠SAB3﹣22,
可得BE,
在△BFE中根据余弦定理,
BF2=EF2+BE2﹣2EF?BEcos∠BEF,
可得cos∠BEF,∴∠BEF=60°,
∴异面直线BE与SC所成角的大小60°.
17.【解答】解:(Ⅰ)CE∥平面O1O2MN.
证明:∵圆台的两个底面互相平行,
∴平面O1O2MN与圆台两个底面的交线平行,
又因为点N为上底圆周上靠近点A的的四等分点,
∴点M为下底圆周上靠近点D的的四等分点,
∴,
∵点E为下底圆弧CD的中点,∴,
∴O2M∥CE,
又O2M?平面O1O2MN,CE?平面O1O2MN,
∴CE∥平面O1O2MN.
(II)当四棱锥P﹣ABCD的体积最大时,也就是点P到平面ABCD的距离最大,
此时点P为上底圆周上的中点.
设圆台的上底面圆的半径为r,则高为r,O2C=2r.
以点O2为坐标原点,建立如图所示的空间直角坐标系,
则C(0,2r,0),P(r,0,r),D(0,﹣2r,0),B(0,r,r),
∴,
则cos,
∴异面直线CP与DB所成角的余弦值为.
当点P在的另一侧中点时,异面直线CP与DB所成角的余弦值也是,
∴异面直线CP与DB所成角的余弦值为.
18.【解答】解:(1)由题意,得,
则该正四棱柱的表面积为8+16,
该正四棱柱的体积为V8.
(2)连接A1C1,DC1,则AC∥A1C1,
∴直线A1D,A1C1所成角就是异面直线A1D,AC所成角,
在△A1DC1中,A1D=DC1=2,A1C1=2,
由余弦定理得cos∠DA1C1
.
∴异面直线A1D与AC所成的角的大小为arccos.
19.【解答】解:(1)如图建立里空间坐标系,A1(2,0,4),E(2,0,2),F(1,1,0),C(0,0,0),
∴(﹣2,0,﹣4),(﹣1,1,﹣2),
∴?2×(﹣1)+0×1+(﹣4)×(﹣2)=10,||2,||,
∴cosθ,
∴θ=arccos.
(2)VC﹣AEF2×2×42×2×42×22.
20.【解答】解:取AD的中点为P,连结PM,PN,
因为点M,N分别为对角线BD,AC的中点,
所以PM∥AB,PN∥CD,且,
则∠MPN为直线AB与CD所成的角或所成角的补角,∠PMN为直线AB与MN所成角或所成角的补角,
又AB=CD,
所以PM=PN,即△PMN为等腰三角形.
(1)若直线AB与MN所成角为60°,即∠PMN=60°,
则∠MPN=180°﹣2×60°=60°,
所以直线AB与CD所成的角为60°;
(2)若直线AB与CD所成的角为θ,则∠MPN=θ或∠MPN=π﹣θ,
若∠MPN=θ,则∠PMN,即直线AB与MN所成角为;
若∠MPN=π﹣θ,则∠PMN,即直线AB与MN所成角为;
综上所述,直线AB与MN所成角为或.
21.【解答】(1)方法一:证明:如图所示,取AE的中点O,连接OF,过点O作OM⊥AC于点M.
因为EC⊥AC,OM,EC?平面ACC1A1,所以OM∥EC.
又因为EC=2FB=2,EC∥FB,
所以OM∥FB且,
所以四边形OMBF为矩形,BM∥OF.
因为OF?平面AEF,BM?平面AEF,
故BM∥平面AEF,此时点M为AC的中点.
(2)解:由(1)知,BM与EF异面,∠OFE就是异面直线BM与EF所成的角或其补角.
可得,,OF⊥AE,
所以,
所以BM与EF所成的角的余弦值为.
方法二:(1)证明:如图所示,取EC的中点P,AC的中点Q,连接PQ,PB,BQ.
因为EC=2FB=2,所以PE∥BF且PE=BF,
所以四边形PEFB为平行四边形,
所以PB∥EF,PQ∥AE,
又AE,EF?平面AEF,PQ,PB?平面AEF,
所以PQ∥平面AFE,PB∥平面AEF,
因为PB∩PQ=P,PB,PQ?平面PBQ,
所以平面PBQ∥平面AEF.
又因为BQ?平面PBQ,所以BQ∥平面AEF.
故点Q即为所求的点M,此时点M为AC的中点.
(2)解:由(1)知,BM与EF异面,
∠MBP就是异面直线BM与EF所成的角或其补角.
可得,,BM⊥AC,
所以,
所以BM与EF所成的角的余弦值为.
22.【解答】解:(1)由题意,,,
则||=||=||=1,且的夹角为60°,
∵(),
∴,
(2),,
∵()?(),
,
∵||,||=1,
设异面直线CF与BD所成角θ,则cosθ=||,
因此异面直线CF与BD所成角的余弦值.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题提高练
第二章《点、直线、平面之间的位置关系》
2.1
空间点、直线、平面之间的位置关系
一.选择题
1.(2020秋?河南月考)设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
A.若α∥β,m?α,n?β,则m∥n
B.若α⊥β,m?α,n?β,则m⊥n
C.若点A,B到α平面的距离相等,则直线AB∥α
D.若m⊥α,m∥β,则α⊥β
2.(2020秋?朝阳区校级期末)在直棱柱ABC﹣A1B1C1中,AB⊥BC,其中AB=BC=BB1=2,点D是AC的中点,则异面直线AB1与BD所成角的大小为( )
A.
B.
C.
D.
3.(2020秋?城关区校级期末)已知l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,则下列命题中不正确的是( )
A.若α∥β,则m⊥α
B.若α∥β,则l⊥m
C.若l⊥m,则l∥β
D.若m∥α,则α⊥β
4.(2020秋?长安区校级期末)在三棱锥P﹣ABC中,PA,PB,PC两两垂直,且PA=PB=PC,M,N分别为AC,AB的中点,则异面直线PN和BM所成角的余弦值为( )
A.
B.
C.
D.
二.填空题
5.(2021?浙江模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为6,点F是棱AA1的中点,AC与BD的交点为O,点M在棱BC上,且BM=2MC,动点T(不同于点M)在四边形ABCD内部及其边界上运动,且TM⊥OF,则直线B1F与TM所成角的余弦值为
.
6.(2020秋?汾阳市期中)如图,在正方体中,A,B,C,D分别是顶点或所在棱的中点,则A,B,C,D四点共面的图形有
(填上所有正确答案的序号).
7.(2020秋?南海区校级月考)如图,在三棱锥A﹣BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则:
(1)当AC,BD满足条件
时,四边形EFGH为菱形;
(2)当AC,BD满足条件
时,四边形EFGH为正方形.
8.(2020秋?河南月考)若正三棱锥A﹣BCD的侧棱长为8,底面边长为4,E,F分别为AC,AD上的动点(如图),则截面△BEF的周长最小值为
.
9.(2020秋?安徽月考)已知四面体ABCD的所有棱长均为6,过D作平面α使得BC∥α,且棱AB,AC分别与平面α交于点E,F,若异面直线DE,BC所成角的余弦值为,则AE的长为
.
10.(2020秋?上城区校级期中)如图,在四面体ABCD中,AB=CD,M、N、P、Q分别是BC、AD、AC、BD的中点,则MN与PQ所成角为
,若AB与CD所成角为30°,则MN和CD所成的角的大小为
.
11.(2020秋?浙江期中)若棱长为4的正四面体A﹣BCD的顶点都在同一球面上,则异面直线AB与CD所成角的余弦值是
,该球的表面积是
.
三.解答题
12.(2020秋?辽阳期末)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(1)证明:AB∥平面C1D1E;
(2)若O为平面A1B1C1D1的中心,求异面直线C1E与AO所成角的余弦值.
13.(2021?虹口区一模)如图在三棱锥P﹣ABC中,棱AB、AC、AP两两垂直,AB=AC=AP=3,点M在AP上,且AM=1.
(1)求异面直线BM和PC所成的角的大小;
(2)求三棱锥P﹣BMC的体积.
14.(2021?闵行区一模)如图,在圆柱OO1中,AB是圆柱的母线,BC是圆柱的底面⊙O的直径,D是底面圆周上异于B、C的点.
(1)求证:CD⊥平面ABD;
(2)若BD=2,CD=4,AC=6,求圆柱OO1的侧面积.
15.(2020秋?金凤区校级月考)如图,在长方体ABCD﹣A′B′C′D′中,AB=3,BC=4,AA′=8,且E,F分别是棱AA′,BB′的中点.求直线A′F与D′E所成角的余弦值.
16.(2020秋?南岗区校级期末)已知正四棱锥S﹣ABCD的侧棱长为,底面的边长为,E是SA的中点,求异面直线BE与SC所成的角.
17.(2020秋?重庆期末)已知圆台O1O2,轴截面ABCD,圆台的上底面圆半径与高相等,下底面圆半径为高的两倍,点E为下底圆弧的中点,点N为上底圆周上靠近点A的的四等分点,经过O1,O2,N三点的平面与弧交于点M,且E,M,N三点在平面ABCD的同侧.
(Ⅰ)判断平面O1O2MN与直线CE的位置关系,并证明你的结论;
(Ⅱ)P为上底圆周上的一个动点,当四棱锥P﹣ABCD的体积最大时,求异面直线CP与DB所成角的余弦值.
18.(2021?嘉定区一模)如图,正四棱柱ABCD﹣A1B1C1D1的底面边长为2,A1D=4.
(1)求该正四棱柱的表面积和体积;
(2)求异面直线A1D与AC所成的角的大小(结果用反三角函数值表示).
19.(2021?徐汇区一模)如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=2,CC1=4,∠ACB=90°,E、F分别为棱AA1、AB的中点.
(1)求异面直线A1C与EF所成的角的大小(结果用反三角函数值表示);
(2)求五棱锥C﹣EFBB1A1的体积.
20.(2020秋?黄浦区校级月考)空间四边形ABCD中,AB=CD,点M、N分别为对角线BD、AC的中点.
(1)若直线AB与MN所成角为60°,求直线AB与CD所成角的大小;
(2)若直线AB与CD所成角为θ,求直线AB与MN所成角的大小.
21.(2020秋?河南月考)如图所示,三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
(1)当点M在何位置时,BM∥平面AEF?
(2)若BM∥平面AEF,判断BM与EF的位置关系,说明理由;并求BM与EF所成的角的余弦值.
22.(2020秋?聊城期中)如图所示,已知空间四边形ABCD的每条边和对角线都等于1,点E,F分别是AB,AD的中点,设,,为空间向量的一组基底,,,,试用基底向量法求解以下各题.求:
(1);
(2)求异面直线CF与BD所成角的余弦值.
参考答案与试题解析
一.选择题
1.【解答】解:由α∥β,m?α,n?β,得m∥n或m与n异面,故A错误;
若α⊥β,m?α,n?β,则m∥n或m与n相交或m与n异面,相交或异面时也不一定垂直,故B错误;
若点A,B到α平面的距离相等,AB可能与α平行,也可能与平面a相交,故C错误;
若m∥β,过m作平面与β相交,交线为n,则m∥n,又m⊥α,所以n⊥α,得α⊥β,故D正确.
故选:D.
2.【解答】解:∵在直棱柱ABC﹣A1B1C1中,AB⊥BC,
∴以B为原点,以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
∵AB=BC=BB1=2,点D是AC的中点,
∴A(0,2,0),B1(0,0,2),B(0,0,0),D(1,1,0),
(0,﹣2,2),(1,1,0),
设异面直线AB1与BD所成角的大小为θ,
则cosθ,
∴θ.
∴异面直线AB1与BD所成角的大小为.
故选:A.
3.【解答】解:因为l,m是两条不同的直线,α,β是两个不同的平面,且l∥α,m⊥β,
若α∥β,则由线面垂直的判定定理得m⊥α,故选项A正确;
若α∥β,则由线面垂直的判定定理得m⊥α,
又l∥α,所以l⊥m,故选项B正确;
若l⊥m,则l与β平行或l?β,故选项C错误;
若m∥α,则由面面垂直的判定定理得α⊥β,故选项D正确.
故选:C.
4.【解答】解:∵在三棱锥P﹣ABC中,PA,PB,PC两两垂直,且PA=PB=PC,M,N分别为AC,AB的中点,
∴以P为原点,PA为x轴,PB为y轴,PC为z轴,建立空间直角坐标系,
设PA=PB=PC=2,则P(0,0,0),N(1,1,0),B(0,2,0),M(1,0,1),
(1,1,0),(1,﹣2,1),
设异面直线PN和BM所成角为θ,
则cosθ.
∴异面直线PN和BM所成角的余弦值为.
故选:D.
二.填空题
5.【解答】解:以A为原点,AD,AB,AA1所在的直线分别为x、y、z轴建立如图所示的空间直角坐标系,
则B1(0,6,6),F(0,0,3),M(4,6,0),O(3,3,0),
设T(x,y,0),则(4﹣x,6﹣y,0),(0,﹣6,﹣3),(﹣3,﹣3,3),
∵TM⊥OF,
∴?0,即﹣3(4﹣x)﹣3(6﹣y)=0,
∴y=10﹣x,
∴(4﹣x,x﹣4,0),
∴|cos,|=||=||=||,
∵点T与点M不重合,∴x﹣4≠0,∴|cos,|,
∴直线B1F与TM所成角的余弦值为.
故答案为:.
6.【解答】解:如图所示:
对于①作中点F,
所以EF∥CD∥AB,则A、B、C、D四点共面.
对于②直线AB和CD
为异面直线,
对于③:如图所示:
连接EF,所以AC∥EF∥BD,
故A、B、C、D四点共面,
对于④:如图所示:
连接EF,GH,
所以AC∥BD∥EF∥GH,
故A、B、C、D四点共面,
对于⑤:直线AB和CD
为异面直线,
故答案为:①③④.
7.【解答】解:(1)因为四边形
EFGH
为菱形,所以
EF=EH,所以
AC=BD.
解:(2)因为四边形
EFGH
为正方形,
所以
EF=EH
且
EF⊥EH,
因为
EF∥AC,EH∥BD,且
,,
所以
AC=BD
且
AC⊥BD.
8.【解答】解:正三棱锥A﹣BCD的侧面展开图如图,
由平面几何知识可得BB'∥CD,
所以∠BEC=∠ECD=∠ACB,
于是△BCE∽△ABC,
所以.
即,
所以CE=2,
所以AE=6,
又,
可得EF=3.
截面△BEF的周长最小值为:4+3+4=11.
故答案为:11.
9.【解答】解:由题意可得EF∥BC,异面直线DE,BC所成的角为∠DEF,且cos∠DEF,
设AE=EF=x(0<x<6),则DE=DF,
于是cos∠DEF,
解得x=2,
即AE的长为2.
故答案为:2.
10.【解答】解:连接MP,NP,MQ,NQ,
∵M、N、P、Q分别为BC、AD、AC、BD的中点,
∴MQ∥CD,MQCD,NP∥CD,NPCD,
∴MQ∥NP,MQ=NP,
∴四边形MPNQ是平行四边形,
∵MPAB,AB=CD,∴MPCD,
∴MP=MQ,
∴平行四边形MPNQ是菱形,
∴MN⊥PQ,
∴MN与PQ所成角为90°.
∵MP∥AB,MQ∥CD,
∴∠PMQ或其补角即为AB与CD所成的角,
∴∠PMQ=30°或150°,
∵MQ∥CD,
∴∠NMQ为MN和CD所成角,
而∠NMQ∠PMQ=15°或75°,
∴MN和CD所成角为15°或75°.
故答案为:90°;15°或75°.
11.【解答】解:取CD中点E,连接BE、AE,
∵棱长为4的正四面体A﹣BCD中,BC=BD,AC=AD,
∴BE⊥CD,AE⊥CD,
∵BE∩AE=E,∴CD⊥平面ABE,
∵AB?平面ABE,∴AB⊥CD,
∴异面直线AB与CD所成角的余弦值是cos0.
过A作AF⊥平面BCD,交BE于F,
棱长为4的正四面体A﹣BCD的顶点都在同一球面上,则球心O在AF上,连结OB,
设球半径为R,
BE2,BF,AF,
∵OB=OA=R,∴OF,
∵OB2=BF2+OF2,∴R2=()2+()2,
解得R,
∴该球的表面积是S=4πR2=4π×6=24π.
故答案为:0,24π.
三.解答题
12.【解答】解:(1)证明:∵在正方体ABCD﹣A1B1C1D1中,AB∥CD∥C1D1,
∴AB∥C1D1,
∵AB?平面C1D1E,C1D1?平面C1D1E,
∴AB∥平面C1D1E.
(2)以D为坐标原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设AB=2,则A(2,0,0),O(1,1,2),C1(0,2,2),E(2,2,1),
∵(2,0,﹣1),(﹣1,1,2),
∴cos,
∴异面直线C1E与AO所成角的余弦值为.
13.【解答】解:(1)在AC上取点N,使ANAC=1,连接MN,BN,
∵AP=3,AM=1,
∴MN∥PC,
∴∠BMN或其补角即为异面直线BM和PC所成的角,
在△BMN中,BM,MN,BN,
由余弦定理知,cos∠BMN,
∴∠BMN=arccos,
∴异面直线BM和PC所成的角的大小为arccos.
(2)V=VP﹣ABC﹣VM﹣ABCS△ABC?(AP﹣AM)3×3×2=3,
故三棱锥P﹣BMC的体积为3.
14.【解答】证明:(1)∵AB⊥底面BCD,∴AB⊥CD,
又CD⊥BD,且AB∩BD=B,
∴CD⊥平面ABD;
解:(2)在Rt△BCD中,由BD=2,CD=4,
得BC,
又在Rt△ABC中,AC=6,得AB.
∴圆柱的底面半径为,母线长为4,
∴圆柱OO1的侧面积为.
15.【解答】解:连接C′F,A′C′,因为E,F分别是棱AA′,BB′的中点.
所以D′E∥C′F,所以直线A′F与D′E所成的角为∠A′FC′或其补角,
在长方体ABCD﹣A′B′C′D′中,AB=3,BC=4,AA′=8,
所以B′F=4,则A′F=5,C′F=4,A′C′=5,
所以cos∠A′FC′,
即直线A′F与D′E所成角的余弦值为.
16.【解答】解:连接底面正方形ABCD对角线AC、BD,交于F,
则F是AC和BD的中点,
连接EF,BD,EF是三角形ASC的中位线,EF∥SC,
且EFSC,则∠BEF或补角即为BE与SC的所成角,
BF,AB,EF,
三角形SAB是等腰三角形,从S作SG⊥AB,
cos∠SAB,
根据余弦定理,BE2=AE2+AB2﹣2AE?AB?cos∠SAB3﹣22,
可得BE,
在△BFE中根据余弦定理,
BF2=EF2+BE2﹣2EF?BEcos∠BEF,
可得cos∠BEF,∴∠BEF=60°,
∴异面直线BE与SC所成角的大小60°.
17.【解答】解:(Ⅰ)CE∥平面O1O2MN.
证明:∵圆台的两个底面互相平行,
∴平面O1O2MN与圆台两个底面的交线平行,
又因为点N为上底圆周上靠近点A的的四等分点,
∴点M为下底圆周上靠近点D的的四等分点,
∴,
∵点E为下底圆弧CD的中点,∴,
∴O2M∥CE,
又O2M?平面O1O2MN,CE?平面O1O2MN,
∴CE∥平面O1O2MN.
(II)当四棱锥P﹣ABCD的体积最大时,也就是点P到平面ABCD的距离最大,
此时点P为上底圆周上的中点.
设圆台的上底面圆的半径为r,则高为r,O2C=2r.
以点O2为坐标原点,建立如图所示的空间直角坐标系,
则C(0,2r,0),P(r,0,r),D(0,﹣2r,0),B(0,r,r),
∴,
则cos,
∴异面直线CP与DB所成角的余弦值为.
当点P在的另一侧中点时,异面直线CP与DB所成角的余弦值也是,
∴异面直线CP与DB所成角的余弦值为.
18.【解答】解:(1)由题意,得,
则该正四棱柱的表面积为8+16,
该正四棱柱的体积为V8.
(2)连接A1C1,DC1,则AC∥A1C1,
∴直线A1D,A1C1所成角就是异面直线A1D,AC所成角,
在△A1DC1中,A1D=DC1=2,A1C1=2,
由余弦定理得cos∠DA1C1
.
∴异面直线A1D与AC所成的角的大小为arccos.
19.【解答】解:(1)如图建立里空间坐标系,A1(2,0,4),E(2,0,2),F(1,1,0),C(0,0,0),
∴(﹣2,0,﹣4),(﹣1,1,﹣2),
∴?2×(﹣1)+0×1+(﹣4)×(﹣2)=10,||2,||,
∴cosθ,
∴θ=arccos.
(2)VC﹣AEF2×2×42×2×42×22.
20.【解答】解:取AD的中点为P,连结PM,PN,
因为点M,N分别为对角线BD,AC的中点,
所以PM∥AB,PN∥CD,且,
则∠MPN为直线AB与CD所成的角或所成角的补角,∠PMN为直线AB与MN所成角或所成角的补角,
又AB=CD,
所以PM=PN,即△PMN为等腰三角形.
(1)若直线AB与MN所成角为60°,即∠PMN=60°,
则∠MPN=180°﹣2×60°=60°,
所以直线AB与CD所成的角为60°;
(2)若直线AB与CD所成的角为θ,则∠MPN=θ或∠MPN=π﹣θ,
若∠MPN=θ,则∠PMN,即直线AB与MN所成角为;
若∠MPN=π﹣θ,则∠PMN,即直线AB与MN所成角为;
综上所述,直线AB与MN所成角为或.
21.【解答】(1)方法一:证明:如图所示,取AE的中点O,连接OF,过点O作OM⊥AC于点M.
因为EC⊥AC,OM,EC?平面ACC1A1,所以OM∥EC.
又因为EC=2FB=2,EC∥FB,
所以OM∥FB且,
所以四边形OMBF为矩形,BM∥OF.
因为OF?平面AEF,BM?平面AEF,
故BM∥平面AEF,此时点M为AC的中点.
(2)解:由(1)知,BM与EF异面,∠OFE就是异面直线BM与EF所成的角或其补角.
可得,,OF⊥AE,
所以,
所以BM与EF所成的角的余弦值为.
方法二:(1)证明:如图所示,取EC的中点P,AC的中点Q,连接PQ,PB,BQ.
因为EC=2FB=2,所以PE∥BF且PE=BF,
所以四边形PEFB为平行四边形,
所以PB∥EF,PQ∥AE,
又AE,EF?平面AEF,PQ,PB?平面AEF,
所以PQ∥平面AFE,PB∥平面AEF,
因为PB∩PQ=P,PB,PQ?平面PBQ,
所以平面PBQ∥平面AEF.
又因为BQ?平面PBQ,所以BQ∥平面AEF.
故点Q即为所求的点M,此时点M为AC的中点.
(2)解:由(1)知,BM与EF异面,
∠MBP就是异面直线BM与EF所成的角或其补角.
可得,,BM⊥AC,
所以,
所以BM与EF所成的角的余弦值为.
22.【解答】解:(1)由题意,,,
则||=||=||=1,且的夹角为60°,
∵(),
∴,
(2),,
∵()?(),
,
∵||,||=1,
设异面直线CF与BD所成角θ,则cosθ=||,
因此异面直线CF与BD所成角的余弦值.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
