【同步必刷题】2.2 直线、平面平行的判定及其性质 基础练(含解析)
文档属性
| 名称 | 【同步必刷题】2.2 直线、平面平行的判定及其性质 基础练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:14:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题基础练
第二章《点、直线、平面之间的位置关系》
2.2
直线、平面平行的判定及其性质
一.选择题
1.(2020秋?成都月考)若α、β、γ是空间中三个不同的平面,α∩β=l,α∩γ=m,γ∩β=n,则l∥m是n∥m的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.(2020秋?三明期中)如图,在正方体ABCD﹣A′B′C′D′中,E、F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有( )
A.4个
B.3个
C.2个
D.1个
3.(2020?浙江学业考试)已知平面α∥平面β,m?α,n?β,那么下列结论正确的是( )
A.m,n是平行直线
B.m,n是异面直线
C.m,n是共面直线
D.m,n是不相交直线
4.(2020秋?香坊区校级期末)已知正方体ABCD﹣A1B1C1D1中,E,F分别是它们所在线段的中点,则满足A1F∥平面BD1E的图形个数为( )
A.0
B.1
C.2
D.3
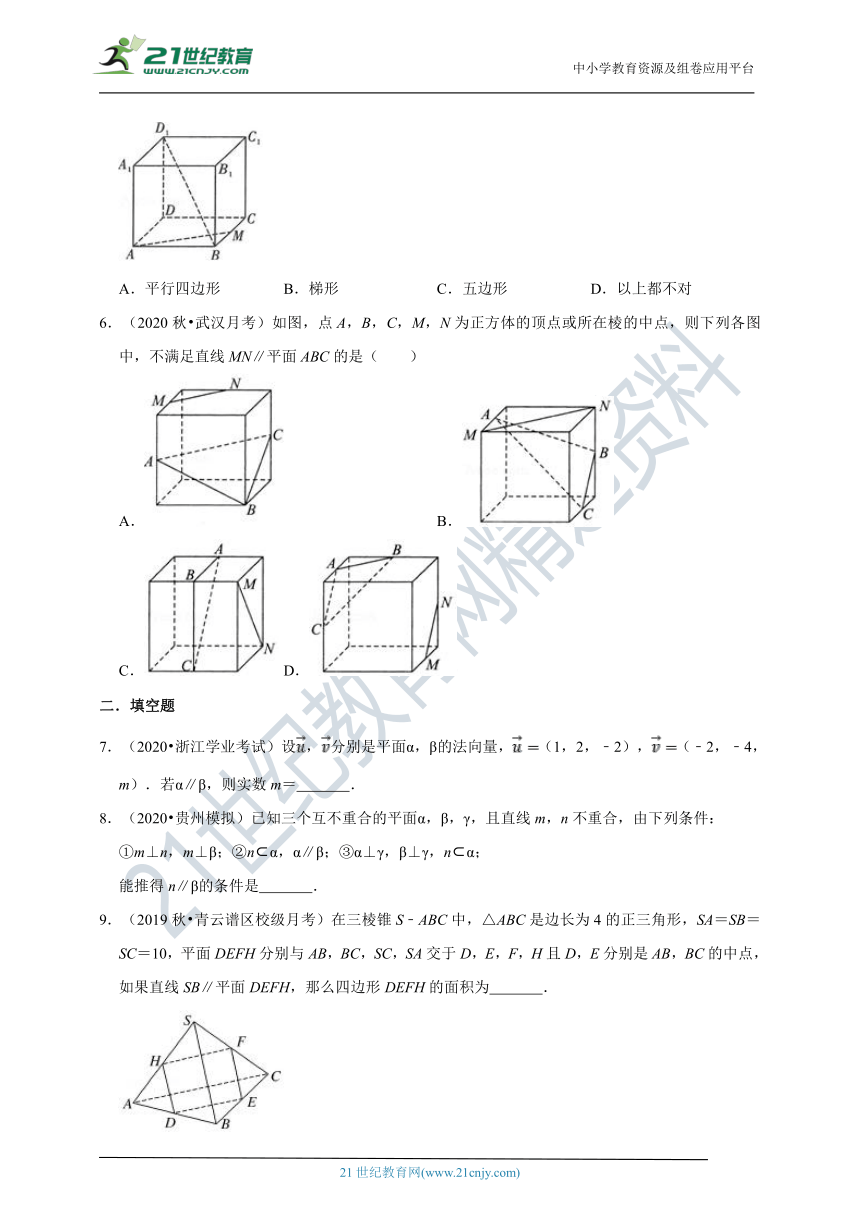
5.(2020秋?12月份月考)如图,在正方体ABCD﹣A1B1C1D1中,点M为棱BC的中点,用平行于体对角线BD1且过点A,M的平面去截正方体ABCD﹣A1B1C1D1,得到的截面的形状是( )
A.平行四边形
B.梯形
C.五边形
D.以上都不对
6.(2020秋?武汉月考)如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线MN∥平面ABC的是( )
A.
B.
C.
D.
二.填空题
7.(2020?浙江学业考试)设,分别是平面α,β的法向量,(1,2,﹣2),(﹣2,﹣4,m).若α∥β,则实数m=
.
8.(2020?贵州模拟)已知三个互不重合的平面α,β,γ,且直线m,n不重合,由下列条件:
①m⊥n,m⊥β;②n?α,α∥β;③α⊥γ,β⊥γ,n?α;
能推得n∥β的条件是
.
9.(2019秋?青云谱区校级月考)在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,SA=SB=SC=10,平面DEFH分别与AB,BC,SC,SA交于D,E,F,H且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为
.
10.(2018秋?庐阳区校级期中)已知平面α,β,直线l,若α∥β,l?α,则直线l与平面β的位置关系为
.
11.(2020秋?富顺县校级期中)已知平面α∥平面β,点S是α,β外一点过S的两条直线AB,CD分别交α于A,C,交β于B,D,若SA=2,SB=4,CD=6,则SC=
.
12.(2020秋?永州月考)已知四棱锥S﹣ABCD的底面是边长为4的正方形,SD⊥面ABCD,点M、N分别是AD、CD的中点,P为SD上一点,且SD=3PD=3,H为正方形ABCD内一点,若SH∥面PMN,则SH的最小值为
.
13.(2020秋?太和县校级月考)已知棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,则过点B1且与平面A1BE平行的正方体的截面面积为
.
三.解答题
14.(2020春?浙江月考)如图,四棱锥P﹣ABCD中,△PAB是等边三角形,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=BC=2,,F,G分别是PC,AD的中点.
(1)①求证:FG∥平面PAB;
②求线段FG的长度.
(2)若PC=3,求直线FG与平面PBC所成角的正弦值.
15.(2019秋?榆林期末)如图,在三棱柱ABC﹣A1B1C1中,△ABC是正三角形,AA1⊥平面ABC,AB=AA1=a,D是BC边上的一点,且AD为∠BAC的平分线.
(1)证明:A1B∥平面ADC1;
(2)若在三棱柱ABC﹣A1B1C1中去掉三棱锥C1﹣ACD后得到的几何体的表面积为318,求a值.
16.(2020?南通模拟)如图所示,已知在五棱锥P﹣ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF,平面PAE与底面ABCDE垂直.求证:
(1)BC∥平面PAE;
(2)PA⊥FC.
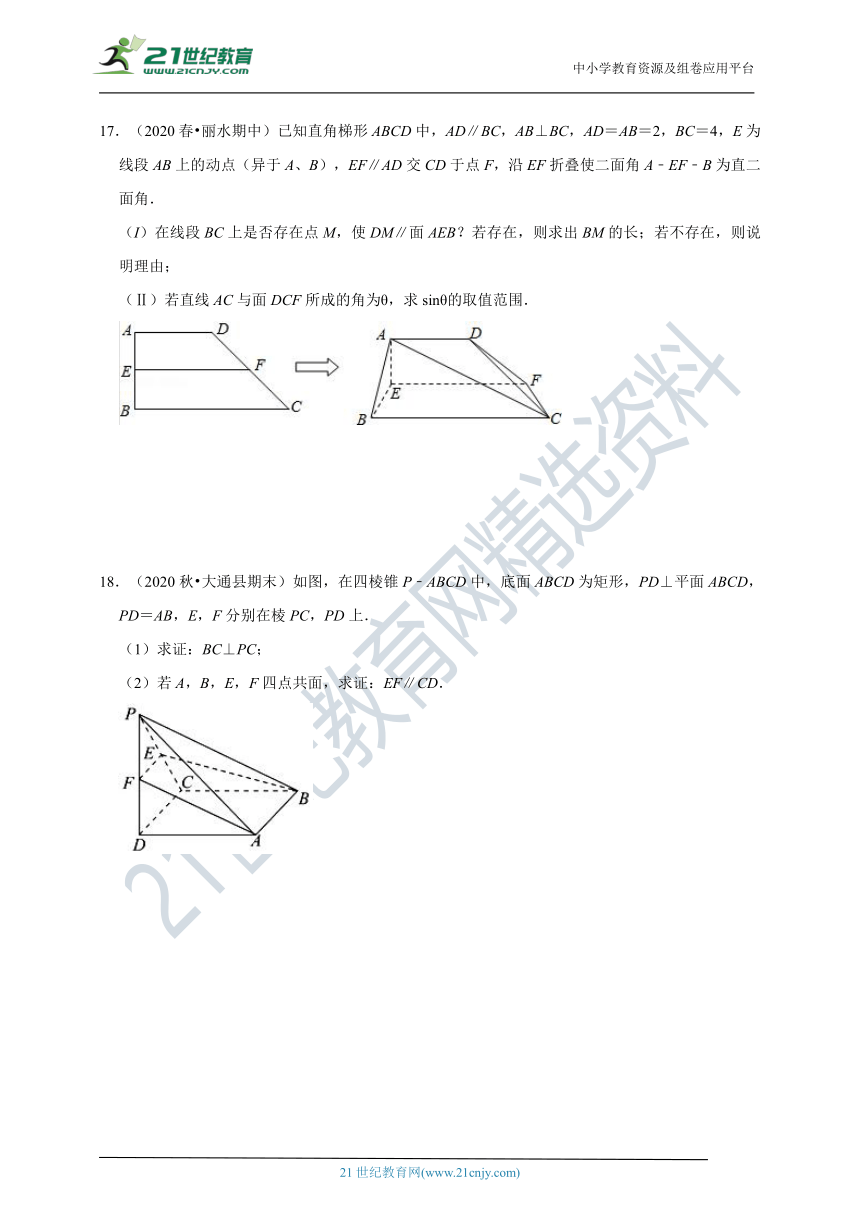
17.(2020春?丽水期中)已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=AB=2,BC=4,E为线段AB上的动点(异于A、B),EF∥AD交CD于点F,沿EF折叠使二面角A﹣EF﹣B为直二面角.
(I)在线段BC上是否存在点M,使DM∥面AEB?若存在,则求出BM的长;若不存在,则说明理由;
(Ⅱ)若直线AC与面DCF所成的角为θ,求sinθ的取值范围.
18.(2020秋?大通县期末)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥平面ABCD,PD=AB,E,F分别在棱PC,PD上.
(1)求证:BC⊥PC;
(2)若A,B,E,F四点共面,求证:EF∥CD.
19.(2021?二十模拟)在如图所示的几何体中,四边形ABCD是菱形,∠BAD=120°,AE⊥平面ABCD,AE∥CF.
(1)求证:DF∥平面ABE;
(2)若AD=AE=2CF=2,求该几何体的表面积.
20.(2020秋?金凤区校级月考)如图,在五面体ABCDEF中,四边形ABCD是矩形,求证:AB∥EF.
21.(2020春?如皋市月考)如图所示,在正方体ABCD﹣A1B1C1D1中,M、N分别为A1C、BC1的中点.求证:
(1)MN∥平面A1B1C1D1;
(2)A1C⊥平面BDC1.
22.(2020?南开区学业考试)如图,在正方体ABCD﹣EFGH中,
(Ⅰ)求证:平面BEG∥平面ACH;
(Ⅱ)求证:DF⊥平面BEG.
参考答案与试题解析
一.选择题
1.【解答】解:根据题意,如图,若l∥m,则m∥平面β,则有m∥n,则l∥m是n∥m的充分条件,
反之:若n∥m,则m∥平面β,则有l∥m,则l∥m是n∥m的必要条件,
故l∥m是n∥m的充要条件,
故选:C.
2.【解答】解:如图,连接AC,A′C′,BD,BD,EF,
则由题意可得EF∥AA′∥CC′,
又EF?平面AA′DD′,EF?平面CC′DD′,EF?平面BB′CC′,EF?平面AA′BB′,
所以EF∥平面AA′DD′,EF∥平面CC′DD′,EF∥平面BB′CC′,EF∥平面AA′BB′,
则正方体的六个面中与EF平行的平面有4个.
故选:A.
3.【解答】解:若平面α∥平面β,m?α,n?β,则m与n的位置关系可以是平行、异面,但一定不相交.
故选:D.
4.【解答】解:①中,平移A1F至D1F′,可知D1F′与面BD1E只有一个交点D1,则A1F与平面BD1E不平行;
②中,由于AF∥DE,而AF?平面BDE,DE?平面BDE,故A1F∥平面BD1E;
③中,平移A1F至D1F′,可知D1F′与面BD1E只有一个交点D1,则A1F与平面BD1E不平行;
故选:B.
5.【解答】解:如图,设截面为α,设BD∩AM=O,P为DD1的靠近于D1的三等分点,
N为CC1的靠近于C的三等分点,
由BD1∥α可得平面BDD1与α的交线平行于BD1,所以α∩平面DBD1=OP,
又平面α与两平行平面AA1D1D,BB1C1C的交线应互相平行,
∴α∩平面BB1C1C=MN,
由MN∥AP且MN≠AP可得截面AMNP为梯形,
故选:B.
6.【解答】解:对于A,作出完整的截面ABCD,由正方体的性质可得MN∥EF∥AC,可得直线MN∥平面ABC,能满足;
对于B,作出完整的截面ABDCEF,由正方体的性质可得MN∥BF,可得直线MN∥平面ABC,能满足;
对于C,作出完整的截面ABCD,由正方体的性质可得MN∥BD,可得直线MN∥平面ABC,能满足;
对于D,作出完整的截面,如下图ABNMHC,可得MN在平面ABC内,不能得出平行,不能满足.
故选:D.
二.填空题
7.【解答】解:,分别是平面α,β的法向量,(1,2,﹣2),(﹣2,﹣4,m),
当α∥β时,λ(1,2,﹣2)=(﹣2,﹣4,m),且λ∈R;
解得λ=﹣2,m=4.
故答案为:4.
8.【解答】解:①m⊥n,m⊥β;可能n?β;
②n?α,α∥β;面面平行的性质得出成立;
③α⊥γ,β⊥γ,n?α;若α与β相交,n可能与β相交,
故答案为:②
9.【解答】解:∵D、E、F、H分别是AB、BC、SA、SC的中点,
∴DE∥AC,FH∥AC,DH∥SB.EF∥SB,
则四边形DEFH是平行四边形,且HDSB5,DEAC2,
取AC的中点O,连结OB,
∵SA=SC=10,AB=BC=4,
∴AC⊥SO,AC⊥OB,
∵S0∩OB=O,
∴AO⊥平面SOB,
∴AO⊥SB,
则HD⊥DE,
即四边形DEFH是矩形,
∴四边形DEFH的面积S10.
故答案为:10.
10.【解答】解:因为平面α∥β,且l?α,
所以l∥β.
故答案为:l∥β.
11.【解答】解:当两个平面在点S的同侧时,如图1所示:
由面面平行的性质定理可得AC∥BD,
所以,由SA=2,AB=SB﹣SA=2,CD=6,解得SC=6;
当点P在两个面的中间时,如图2所示:
由AC∥BD,可得,
所以SCCD=2.
综上知,SC的值为6或2.
故答案为:2或6.
12.【解答】解:如图所示:
四棱锥S﹣ABCD中,SD⊥平面ABCD,BD?平面ABCD,所以SD⊥BD;
由点M、N分别是AD、CD的中点,所以MN∥AC;
又SD=3PD=3,取OB的中点H,连接SH,
则,
所以PQ∥SH;
又PQ?平面PMN,SH?平面PMN,
所以SH∥平面PMN.
所以SH的最小值为.
故答案为:3.
13.【解答】解:取ED的中点F,取G,使A1G,取H使BHBC,连接GH,FH,GB1,由平行性质可知:FH∥GB1且FH=GB1,即四边形FHB1G为平行四边形,
∵棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,AEAD,
∴BE∥FH,A1E∥GF,∴BE∥面FHB1G,A1E∥面FHB1G,
∵A1E∩EB=E,
∴面A1BE∥面FHB1G,
∵FH=EB,FG=A1E,
∴四边形FHB1G为菱形,,
∴2,.
截面面积S..
故答案为:,
三.解答题
14.【解答】解:(1)①证明:取BC的中点I,则GI∥AB,FI∥PB,
∵GI∩FI=I,AB∩BP=B,
∴平面GFI∥平面PAB,
∴FG∥平面PAB;
②由①可知,,
由余弦定理有,.
(2)∵,
∴∠POC=120°,
又EO⊥AB,OC⊥AB,
∴AB⊥平面POC,
∴平面POC⊥平面ABC,
延长CO到H,使得PH⊥OH,则PH⊥平面ABC,,
∵PB=BC=2,PC=3,
∴,
设G到平面PBC的距离设为h,则,
∴,
∴直线FG与平面PBC所成角的正弦值为.
15.【解答】(1)证明:如图,连接A1C交AC1于点E,连接DE,易知E是A1C的中点,
因为△ABC是正三角形,且AD为∠BAC的平分线,所以D是BC的中点,
所以DE是△A1BC的中位线,A1B∥DE.
因为A1B?平面ADC1,DE?平面ADC1,所以A1B∥平面ADC1.
(2)解:设剩余的几何体的表面积为S,
则,.
易证平面ABC⊥平面BCC1,
因为AD⊥BC,所以AD⊥平面BCC1,所以AD⊥DC1,
可得△ADC1的面积为,
所以.
因为,所以.
16.【解答】证明:(1)如图,凸五边形ABCDE,延长AE、CD交于点H.
∵∠AED=∠EDC=120°,
∴∠HED=∠HDE=60°,∴△HED为等边三角形,
∠H=60°.
∴∠H+∠BCD=60°+120°=180°,
∴BC∥AE.
又∵AE?平面PAE,BC?平面PAE,
∴BC∥平面PAE;
(2)如图,连结AC.
∵△HED是等边三角形,
∴HE=HD=ED=1,
∴HC=HA=3.
又∵∠H=60°,
∴△HAC为等边三角形.
又∵AFAH,
∴CF⊥AE.
∵平面PAE⊥平面ABCDE,平面PAE∩平面ABCDE=AE,CF?平面ABCDE,
∴CF⊥平面PAE.
又∵PA?平面PAE,
∴PA⊥FC.
17.【解答】解:(Ⅰ)假设在线段BC上存在点M,使DM∥面AEB,则DM∥AB即可,
∵DM∥AB,AB?平面ABE,DM?平面ABE,
∴DM∥面AEB,
∵AD∥BC,M∈BC,∴AD∥BM,又DM∥AB,
∴四边形ABMD是平行四边形,
∴BM=AD=2.
(Ⅱ)以E为原点,EA为x轴,EF为y轴,EA为z轴,建立空间直角坐标系,
设BE=a,则EA=2﹣a,
∴B(a,0,0),A(0,0,2﹣a),C(a,4,0),E(0,0,0),F(0,4﹣a,0),D(0,2,2﹣a),
(a,4,a﹣2),(a,2,a﹣2),(0,2﹣a,a﹣2),
∴,0<a<2,
∴(﹣1,1,1),
∴cos,
∵直线AC与面DCF所成的角为θ,
∴sinθ=cos.
∴.
18.【解答】证明:(1)∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC,
∵四边形ABCD为矩形,
∴CD⊥BC,
又PD∩CD=D,PD,CD?平面PCD.
∴BC⊥平面PCD,
又PC?平面PCD,
∴BC⊥PC.
(2)∵四边形ABCD为矩形,
∴AB∥CD.
又CD?平面PCD,AB?平面PCD,
∴AB∥平面PCD.
又由题意,得平面ABEF∩平面PCD=EF,AB?平面ABEF,
∴AB∥EF,
∴EF∥CD.
19.【解答】解:(1)证明:因为AE∥CF,CF?平面ABE,
所以CF∥平面ABE,
因为四边形ABCD是菱形,
所以CD∥AB,
由于CD?平面ABE,
所以CD∥平面ABE,
又CF∩CD=C,
所以平面CDF∥平面ABE,
又DF?平面CDF,
所以DF∥平面ABE.
(2)由AE∥CF,知A,C,F,E四点共面,
连接AC,于是该几何体是由两个相同的四棱锥B﹣ACFE,D﹣ACFE构成的,
由题意知,S△ABE2,S△ABC,S△BCF1,
在△BEF中,EF,BE=2,BF,S△BEF,
所以该几何体的表面积为2×(S△ABE+S△ABC+S△BCF+S△BEF)=6+22.
20.【解答】证明:在五面体ABCDEF中,因为四边形ABCD是矩形,
所以AB∥CD.
因为AB?平面CDEF,CD?平面CDEF,
所以AB∥平面CDEF.
因为AB?平面ABFE,平面ABFE∩平面CDEF=EF,
所以AB∥EF.
21.【解答】证明:(1)连接B1C,
由正方体的性质知,四边形B1BCC1为正方形,
∵N为BC1的中点,∴N也为B1C的中点,
又M为A1C的中点,∴MN∥A1B1,
∵A1B1?平面A1B1C1D1,MN?平面A1B1C1D1,
∴MN∥平面A1B1C1D1.
(2)连接AC,
由正方体的性质知,A1B1⊥平面B1BCC1,
∵BC1?平面B1BCC1,∴A1B1⊥BC1,
又B1C⊥BC1,A1B1∩B1C=B1,A1B1、B1C?平面A1B1C,
∴BC1⊥平面A1B1C,∴BC1⊥A1C.
由正方体的性质知,AA1⊥平面ABCD,
∵BD?平面ABCD,∴AA1⊥BD,
又BD⊥AC,AA1∩AC=A,AA1、AC?平面A1AC,
∴BD⊥平面A1AC,∴BD⊥A1C.
∵BC1∩BD=B,BC1、BD?平面BDC1,
∴A1C⊥平面BDC1.
22.【解答】证明:(Ⅰ)∵四边形BEHC和四边形ABGH为平行四边形,
∴BE∥CH,BG∥AH,
又BE,BG?平面BEG,且CH,AH?平面BEG,
∴CH∥平面BEG,AH∥平面BEG.
又CH,AH?平面ACH,且CH∩AH=H,
∴平面BEG∥平面ACH;
(Ⅱ)连结HF,∵DH⊥平面EFGH,且EG?平面EFGH,∴DH⊥EG.
∵EG⊥HF,又HF∩DH=H,∴EG⊥平面HDF.
∵DF?平面HDF,∴EG⊥DF.
同理可得EB⊥DF.
∵EG∩EB=E,
∴DF⊥平面BEG.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题基础练
第二章《点、直线、平面之间的位置关系》
2.2
直线、平面平行的判定及其性质
一.选择题
1.(2020秋?成都月考)若α、β、γ是空间中三个不同的平面,α∩β=l,α∩γ=m,γ∩β=n,则l∥m是n∥m的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.(2020秋?三明期中)如图,在正方体ABCD﹣A′B′C′D′中,E、F分别为平面ABCD和平面A′B′C′D′的中心,则正方体的六个面中与EF平行的平面有( )
A.4个
B.3个
C.2个
D.1个
3.(2020?浙江学业考试)已知平面α∥平面β,m?α,n?β,那么下列结论正确的是( )
A.m,n是平行直线
B.m,n是异面直线
C.m,n是共面直线
D.m,n是不相交直线
4.(2020秋?香坊区校级期末)已知正方体ABCD﹣A1B1C1D1中,E,F分别是它们所在线段的中点,则满足A1F∥平面BD1E的图形个数为( )
A.0
B.1
C.2
D.3
5.(2020秋?12月份月考)如图,在正方体ABCD﹣A1B1C1D1中,点M为棱BC的中点,用平行于体对角线BD1且过点A,M的平面去截正方体ABCD﹣A1B1C1D1,得到的截面的形状是( )
A.平行四边形
B.梯形
C.五边形
D.以上都不对
6.(2020秋?武汉月考)如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,不满足直线MN∥平面ABC的是( )
A.
B.
C.
D.
二.填空题
7.(2020?浙江学业考试)设,分别是平面α,β的法向量,(1,2,﹣2),(﹣2,﹣4,m).若α∥β,则实数m=
.
8.(2020?贵州模拟)已知三个互不重合的平面α,β,γ,且直线m,n不重合,由下列条件:
①m⊥n,m⊥β;②n?α,α∥β;③α⊥γ,β⊥γ,n?α;
能推得n∥β的条件是
.
9.(2019秋?青云谱区校级月考)在三棱锥S﹣ABC中,△ABC是边长为4的正三角形,SA=SB=SC=10,平面DEFH分别与AB,BC,SC,SA交于D,E,F,H且D,E分别是AB,BC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为
.
10.(2018秋?庐阳区校级期中)已知平面α,β,直线l,若α∥β,l?α,则直线l与平面β的位置关系为
.
11.(2020秋?富顺县校级期中)已知平面α∥平面β,点S是α,β外一点过S的两条直线AB,CD分别交α于A,C,交β于B,D,若SA=2,SB=4,CD=6,则SC=
.
12.(2020秋?永州月考)已知四棱锥S﹣ABCD的底面是边长为4的正方形,SD⊥面ABCD,点M、N分别是AD、CD的中点,P为SD上一点,且SD=3PD=3,H为正方形ABCD内一点,若SH∥面PMN,则SH的最小值为
.
13.(2020秋?太和县校级月考)已知棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,则过点B1且与平面A1BE平行的正方体的截面面积为
.
三.解答题
14.(2020春?浙江月考)如图,四棱锥P﹣ABCD中,△PAB是等边三角形,底面ABCD是直角梯形,AB∥CD,AB⊥AD,AB=BC=2,,F,G分别是PC,AD的中点.
(1)①求证:FG∥平面PAB;
②求线段FG的长度.
(2)若PC=3,求直线FG与平面PBC所成角的正弦值.
15.(2019秋?榆林期末)如图,在三棱柱ABC﹣A1B1C1中,△ABC是正三角形,AA1⊥平面ABC,AB=AA1=a,D是BC边上的一点,且AD为∠BAC的平分线.
(1)证明:A1B∥平面ADC1;
(2)若在三棱柱ABC﹣A1B1C1中去掉三棱锥C1﹣ACD后得到的几何体的表面积为318,求a值.
16.(2020?南通模拟)如图所示,已知在五棱锥P﹣ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF,平面PAE与底面ABCDE垂直.求证:
(1)BC∥平面PAE;
(2)PA⊥FC.
17.(2020春?丽水期中)已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD=AB=2,BC=4,E为线段AB上的动点(异于A、B),EF∥AD交CD于点F,沿EF折叠使二面角A﹣EF﹣B为直二面角.
(I)在线段BC上是否存在点M,使DM∥面AEB?若存在,则求出BM的长;若不存在,则说明理由;
(Ⅱ)若直线AC与面DCF所成的角为θ,求sinθ的取值范围.
18.(2020秋?大通县期末)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥平面ABCD,PD=AB,E,F分别在棱PC,PD上.
(1)求证:BC⊥PC;
(2)若A,B,E,F四点共面,求证:EF∥CD.
19.(2021?二十模拟)在如图所示的几何体中,四边形ABCD是菱形,∠BAD=120°,AE⊥平面ABCD,AE∥CF.
(1)求证:DF∥平面ABE;
(2)若AD=AE=2CF=2,求该几何体的表面积.
20.(2020秋?金凤区校级月考)如图,在五面体ABCDEF中,四边形ABCD是矩形,求证:AB∥EF.
21.(2020春?如皋市月考)如图所示,在正方体ABCD﹣A1B1C1D1中,M、N分别为A1C、BC1的中点.求证:
(1)MN∥平面A1B1C1D1;
(2)A1C⊥平面BDC1.
22.(2020?南开区学业考试)如图,在正方体ABCD﹣EFGH中,
(Ⅰ)求证:平面BEG∥平面ACH;
(Ⅱ)求证:DF⊥平面BEG.
参考答案与试题解析
一.选择题
1.【解答】解:根据题意,如图,若l∥m,则m∥平面β,则有m∥n,则l∥m是n∥m的充分条件,
反之:若n∥m,则m∥平面β,则有l∥m,则l∥m是n∥m的必要条件,
故l∥m是n∥m的充要条件,
故选:C.
2.【解答】解:如图,连接AC,A′C′,BD,BD,EF,
则由题意可得EF∥AA′∥CC′,
又EF?平面AA′DD′,EF?平面CC′DD′,EF?平面BB′CC′,EF?平面AA′BB′,
所以EF∥平面AA′DD′,EF∥平面CC′DD′,EF∥平面BB′CC′,EF∥平面AA′BB′,
则正方体的六个面中与EF平行的平面有4个.
故选:A.
3.【解答】解:若平面α∥平面β,m?α,n?β,则m与n的位置关系可以是平行、异面,但一定不相交.
故选:D.
4.【解答】解:①中,平移A1F至D1F′,可知D1F′与面BD1E只有一个交点D1,则A1F与平面BD1E不平行;
②中,由于AF∥DE,而AF?平面BDE,DE?平面BDE,故A1F∥平面BD1E;
③中,平移A1F至D1F′,可知D1F′与面BD1E只有一个交点D1,则A1F与平面BD1E不平行;
故选:B.
5.【解答】解:如图,设截面为α,设BD∩AM=O,P为DD1的靠近于D1的三等分点,
N为CC1的靠近于C的三等分点,
由BD1∥α可得平面BDD1与α的交线平行于BD1,所以α∩平面DBD1=OP,
又平面α与两平行平面AA1D1D,BB1C1C的交线应互相平行,
∴α∩平面BB1C1C=MN,
由MN∥AP且MN≠AP可得截面AMNP为梯形,
故选:B.
6.【解答】解:对于A,作出完整的截面ABCD,由正方体的性质可得MN∥EF∥AC,可得直线MN∥平面ABC,能满足;
对于B,作出完整的截面ABDCEF,由正方体的性质可得MN∥BF,可得直线MN∥平面ABC,能满足;
对于C,作出完整的截面ABCD,由正方体的性质可得MN∥BD,可得直线MN∥平面ABC,能满足;
对于D,作出完整的截面,如下图ABNMHC,可得MN在平面ABC内,不能得出平行,不能满足.
故选:D.
二.填空题
7.【解答】解:,分别是平面α,β的法向量,(1,2,﹣2),(﹣2,﹣4,m),
当α∥β时,λ(1,2,﹣2)=(﹣2,﹣4,m),且λ∈R;
解得λ=﹣2,m=4.
故答案为:4.
8.【解答】解:①m⊥n,m⊥β;可能n?β;
②n?α,α∥β;面面平行的性质得出成立;
③α⊥γ,β⊥γ,n?α;若α与β相交,n可能与β相交,
故答案为:②
9.【解答】解:∵D、E、F、H分别是AB、BC、SA、SC的中点,
∴DE∥AC,FH∥AC,DH∥SB.EF∥SB,
则四边形DEFH是平行四边形,且HDSB5,DEAC2,
取AC的中点O,连结OB,
∵SA=SC=10,AB=BC=4,
∴AC⊥SO,AC⊥OB,
∵S0∩OB=O,
∴AO⊥平面SOB,
∴AO⊥SB,
则HD⊥DE,
即四边形DEFH是矩形,
∴四边形DEFH的面积S10.
故答案为:10.
10.【解答】解:因为平面α∥β,且l?α,
所以l∥β.
故答案为:l∥β.
11.【解答】解:当两个平面在点S的同侧时,如图1所示:
由面面平行的性质定理可得AC∥BD,
所以,由SA=2,AB=SB﹣SA=2,CD=6,解得SC=6;
当点P在两个面的中间时,如图2所示:
由AC∥BD,可得,
所以SCCD=2.
综上知,SC的值为6或2.
故答案为:2或6.
12.【解答】解:如图所示:
四棱锥S﹣ABCD中,SD⊥平面ABCD,BD?平面ABCD,所以SD⊥BD;
由点M、N分别是AD、CD的中点,所以MN∥AC;
又SD=3PD=3,取OB的中点H,连接SH,
则,
所以PQ∥SH;
又PQ?平面PMN,SH?平面PMN,
所以SH∥平面PMN.
所以SH的最小值为.
故答案为:3.
13.【解答】解:取ED的中点F,取G,使A1G,取H使BHBC,连接GH,FH,GB1,由平行性质可知:FH∥GB1且FH=GB1,即四边形FHB1G为平行四边形,
∵棱长为2的正方体ABCD﹣A1B1C1D1中,E在棱AD上,且2AE=DE,AEAD,
∴BE∥FH,A1E∥GF,∴BE∥面FHB1G,A1E∥面FHB1G,
∵A1E∩EB=E,
∴面A1BE∥面FHB1G,
∵FH=EB,FG=A1E,
∴四边形FHB1G为菱形,,
∴2,.
截面面积S..
故答案为:,
三.解答题
14.【解答】解:(1)①证明:取BC的中点I,则GI∥AB,FI∥PB,
∵GI∩FI=I,AB∩BP=B,
∴平面GFI∥平面PAB,
∴FG∥平面PAB;
②由①可知,,
由余弦定理有,.
(2)∵,
∴∠POC=120°,
又EO⊥AB,OC⊥AB,
∴AB⊥平面POC,
∴平面POC⊥平面ABC,
延长CO到H,使得PH⊥OH,则PH⊥平面ABC,,
∵PB=BC=2,PC=3,
∴,
设G到平面PBC的距离设为h,则,
∴,
∴直线FG与平面PBC所成角的正弦值为.
15.【解答】(1)证明:如图,连接A1C交AC1于点E,连接DE,易知E是A1C的中点,
因为△ABC是正三角形,且AD为∠BAC的平分线,所以D是BC的中点,
所以DE是△A1BC的中位线,A1B∥DE.
因为A1B?平面ADC1,DE?平面ADC1,所以A1B∥平面ADC1.
(2)解:设剩余的几何体的表面积为S,
则,.
易证平面ABC⊥平面BCC1,
因为AD⊥BC,所以AD⊥平面BCC1,所以AD⊥DC1,
可得△ADC1的面积为,
所以.
因为,所以.
16.【解答】证明:(1)如图,凸五边形ABCDE,延长AE、CD交于点H.
∵∠AED=∠EDC=120°,
∴∠HED=∠HDE=60°,∴△HED为等边三角形,
∠H=60°.
∴∠H+∠BCD=60°+120°=180°,
∴BC∥AE.
又∵AE?平面PAE,BC?平面PAE,
∴BC∥平面PAE;
(2)如图,连结AC.
∵△HED是等边三角形,
∴HE=HD=ED=1,
∴HC=HA=3.
又∵∠H=60°,
∴△HAC为等边三角形.
又∵AFAH,
∴CF⊥AE.
∵平面PAE⊥平面ABCDE,平面PAE∩平面ABCDE=AE,CF?平面ABCDE,
∴CF⊥平面PAE.
又∵PA?平面PAE,
∴PA⊥FC.
17.【解答】解:(Ⅰ)假设在线段BC上存在点M,使DM∥面AEB,则DM∥AB即可,
∵DM∥AB,AB?平面ABE,DM?平面ABE,
∴DM∥面AEB,
∵AD∥BC,M∈BC,∴AD∥BM,又DM∥AB,
∴四边形ABMD是平行四边形,
∴BM=AD=2.
(Ⅱ)以E为原点,EA为x轴,EF为y轴,EA为z轴,建立空间直角坐标系,
设BE=a,则EA=2﹣a,
∴B(a,0,0),A(0,0,2﹣a),C(a,4,0),E(0,0,0),F(0,4﹣a,0),D(0,2,2﹣a),
(a,4,a﹣2),(a,2,a﹣2),(0,2﹣a,a﹣2),
∴,0<a<2,
∴(﹣1,1,1),
∴cos,
∵直线AC与面DCF所成的角为θ,
∴sinθ=cos.
∴.
18.【解答】证明:(1)∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC,
∵四边形ABCD为矩形,
∴CD⊥BC,
又PD∩CD=D,PD,CD?平面PCD.
∴BC⊥平面PCD,
又PC?平面PCD,
∴BC⊥PC.
(2)∵四边形ABCD为矩形,
∴AB∥CD.
又CD?平面PCD,AB?平面PCD,
∴AB∥平面PCD.
又由题意,得平面ABEF∩平面PCD=EF,AB?平面ABEF,
∴AB∥EF,
∴EF∥CD.
19.【解答】解:(1)证明:因为AE∥CF,CF?平面ABE,
所以CF∥平面ABE,
因为四边形ABCD是菱形,
所以CD∥AB,
由于CD?平面ABE,
所以CD∥平面ABE,
又CF∩CD=C,
所以平面CDF∥平面ABE,
又DF?平面CDF,
所以DF∥平面ABE.
(2)由AE∥CF,知A,C,F,E四点共面,
连接AC,于是该几何体是由两个相同的四棱锥B﹣ACFE,D﹣ACFE构成的,
由题意知,S△ABE2,S△ABC,S△BCF1,
在△BEF中,EF,BE=2,BF,S△BEF,
所以该几何体的表面积为2×(S△ABE+S△ABC+S△BCF+S△BEF)=6+22.
20.【解答】证明:在五面体ABCDEF中,因为四边形ABCD是矩形,
所以AB∥CD.
因为AB?平面CDEF,CD?平面CDEF,
所以AB∥平面CDEF.
因为AB?平面ABFE,平面ABFE∩平面CDEF=EF,
所以AB∥EF.
21.【解答】证明:(1)连接B1C,
由正方体的性质知,四边形B1BCC1为正方形,
∵N为BC1的中点,∴N也为B1C的中点,
又M为A1C的中点,∴MN∥A1B1,
∵A1B1?平面A1B1C1D1,MN?平面A1B1C1D1,
∴MN∥平面A1B1C1D1.
(2)连接AC,
由正方体的性质知,A1B1⊥平面B1BCC1,
∵BC1?平面B1BCC1,∴A1B1⊥BC1,
又B1C⊥BC1,A1B1∩B1C=B1,A1B1、B1C?平面A1B1C,
∴BC1⊥平面A1B1C,∴BC1⊥A1C.
由正方体的性质知,AA1⊥平面ABCD,
∵BD?平面ABCD,∴AA1⊥BD,
又BD⊥AC,AA1∩AC=A,AA1、AC?平面A1AC,
∴BD⊥平面A1AC,∴BD⊥A1C.
∵BC1∩BD=B,BC1、BD?平面BDC1,
∴A1C⊥平面BDC1.
22.【解答】证明:(Ⅰ)∵四边形BEHC和四边形ABGH为平行四边形,
∴BE∥CH,BG∥AH,
又BE,BG?平面BEG,且CH,AH?平面BEG,
∴CH∥平面BEG,AH∥平面BEG.
又CH,AH?平面ACH,且CH∩AH=H,
∴平面BEG∥平面ACH;
(Ⅱ)连结HF,∵DH⊥平面EFGH,且EG?平面EFGH,∴DH⊥EG.
∵EG⊥HF,又HF∩DH=H,∴EG⊥平面HDF.
∵DF?平面HDF,∴EG⊥DF.
同理可得EB⊥DF.
∵EG∩EB=E,
∴DF⊥平面BEG.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
