【同步必刷题】4.3 空间直角坐标系 基础练(含解析)
文档属性
| 名称 | 【同步必刷题】4.3 空间直角坐标系 基础练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:46:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题基础练
第四章《圆与方程》
4.3
空间直角坐标系
一.选择题
1.(2020秋?天津期末)在空间直角坐标系中,已知点A(2,﹣1,3),B(﹣4,1,﹣1),则线段AB的中点坐标是( )
A.(﹣1,0,2)
B.(﹣1,0,1)
C.(3,0,1)
D.(﹣1,1,1)
2.(2020秋?和平区校级月考)在空间直角坐标系中,已知点A(4,﹣3,5),B(﹣2,1,﹣7),则线段AB的中点坐标是( )
A.(2,﹣2,﹣2)
B.(1,﹣1,﹣1)
C.(1,1,1)
D.(2,2,2)
3.(2020秋?山东月考)点A(2,﹣1,3)关于xOy平面的对称点为( )
A.(2,﹣1,﹣3)
B.(2,1,3)
C.(﹣2,1,3)
D.(﹣2,﹣1,3)
4.(2020秋?汾阳市期中)在空间直角坐标系O﹣xyz中,点A(﹣1,0,3)关于坐标原点的对称点为B,则|AB|=( )
A.2
B.
C.
D.10
5.(2020春?荔湾区期中)在空间直角坐标系中,A(2,3,5),B(3,1,4)两点之间的距离为( )
A.
B.2
C.
D.
6.(2020秋?涪城区校级期中)空间直角坐标系中,点B(2,1,6)关于xOz平面的对称点为C,则A(﹣3,4,0)与C的距离为( )
A.2
B.2
C.
D.9
7.(2020秋?新泰市校级期中)已知A(1,﹣2,3)、B(2,1,﹣1)两点,则直线AB与空间直角坐标系中的yOz平面的交点坐标为( )
A.(0,0,0)
B.(0,﹣5,7)
C.()
D.()
二.填空题
8.(2020秋?辽阳期末)已知A(5,﹣7),B(3,﹣1),且C与A关于点B对称,则C的坐标为
.
9.(2020秋?庐阳区校级期中)在空间直角坐标系O﹣xyz中,若点A(1,2,3),B(1,﹣1,4),点C是点A关于平面yOz的对称点,则点B与C的距离为
.
10.(2020秋?黎川县校级期中)在空间直角坐标系中,点M(1,﹣2,3)关于平面yOz对称的点的坐标是
.
11.(2020秋?西城区校级期中)在空间直角坐标系中点A=(﹣1,1,﹣2)关于x轴的对称点的坐标是
.
12.(2020秋?浙江月考)在空间直角坐标系中,点P(4,﹣2,3)到原点的距离为
,关于z轴对称的点的坐标为
.
13.(2020春?越秀区期末)在空间直角坐标系中,已知点A(2,3,4),B(3,1,1),点M在平面xOy上,则|MA|+|MB|的最小值为
.
14.(2020秋?黎川县校级期中)在空间直角坐标系中,若A(3,﹣6,0),B(7,2,z),|AB|=12,则z=
.
15.(2019秋?淮南期末)若两点A(x,5﹣x,2x﹣1),B(1,x+2,2﹣x),当||取最小值时,x的值等于
.
三.解答题
16.已知点A(﹣4,2,3)关于坐标原点的对称点为A1,A1关于xOz平面的对称点为A2,A2关于z轴的对称点为A3,求线段AA3的中点M的坐标.
17.已知点A(2,4,0),B(1,3,3),在直线AB上有一点Q,使得2,求点Q的坐标.
18.已知A(2,5,﹣6),在y轴上求一点P,使PA=7.
19.分别根据下列条件,求空间两点P1,P2间的距离:
(1)P1(2,﹣2,0),P2(4,0,1);
(2)P1(1,﹣1,3),P2(1,2,﹣1).
20.(2017秋?大方县校级月考)若点P(﹣4,﹣2,3)关于坐标平面xOy及y轴的对称点的坐标分别是A和B.
求线段AB的长.
21.(2015秋?怀柔区期末)已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A﹣xyz.
(Ⅰ)求点A,B,C,D,P,E的坐标;
(Ⅱ)求.
22.(2013秋?船山区校级月考)已知△ABC的三个顶点A(1,﹣1,7),B(3,﹣2,5),C(2,﹣3,9).
(1)试求△ABC的各边之长;
(2)求三角形的三个内角的大小;
(3)写出△ABC的重心坐标.
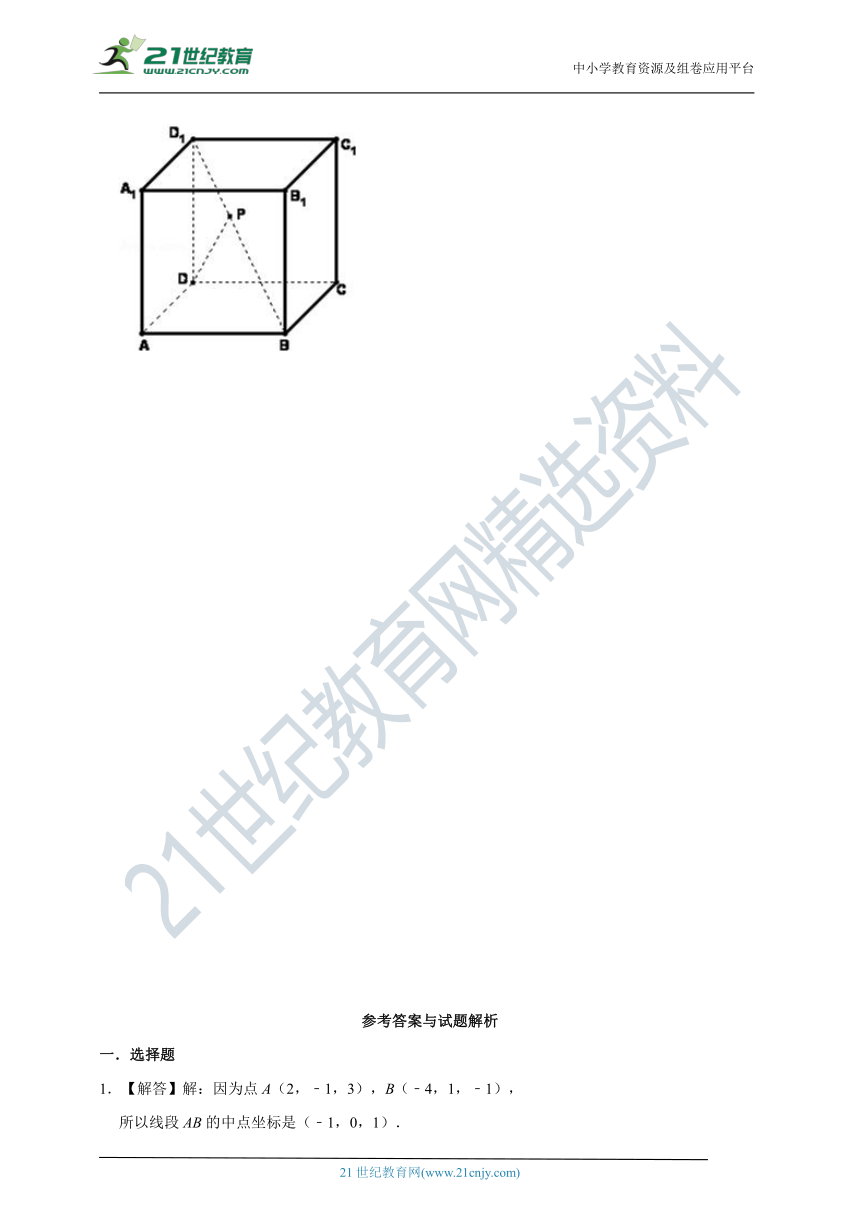
23.(2012秋?临汾校级期中)如图,已知正方体ABCD﹣A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:因为点A(2,﹣1,3),B(﹣4,1,﹣1),
所以线段AB的中点坐标是(﹣1,0,1).
故选:B.
2.【解答】解:在空间直角坐标系中,
点A(4,﹣3,5),B(﹣2,1,﹣7),
则线段AB的中点坐标是(1,﹣1,﹣1).
故选:B.
3.【解答】解:点A(2,﹣1,3)关于xOy平面的对称点为(2,﹣1,﹣3).
故选:A.
4.【解答】解:由题意得:
点A(﹣1,0,3)关于坐标原点的对称点B(1,0,﹣3),
则|AB|2,
故选:C.
5.【解答】解:在空间直角坐标系中,A(2,3,5),B(3,1,4),
两点之间的距离为:.
故选:D.
6.【解答】解:∵空间直角坐标系中,点B(2,1,6)关于xOz平面的对称点为C,
∴点C的坐标为C(2,﹣1,6).
A(﹣3,4,0)与C的距离为:
故选:C.
7.【解答】解:设C点为(0,a,b),则由题意得,
解得a=﹣5,b=7,
所以C点坐标为(0,﹣5,7).
故选:B.
二.填空题
8.【解答】解:设C(x,y),
∵A(5,﹣7),B(3,﹣1),且C与A关于点B对称,
∴,即(﹣2,6)=(x﹣3,y+1),
∴,解得x=1,y=5.
∴C的坐标为(1,5).
故答案为:(1,5).
9.【解答】解:空间直角坐标系O﹣xyz中,点A(1,2,3),B(1,﹣1,4),
则点A关于平面yOz的对称点为C(﹣1,2,3),
所以点B与C的距离为|BC|.
故答案为:.
10.【解答】解:空间直角坐标系中,点M(1,﹣2,3)关于平面yOz对称的点的坐标是(﹣1,﹣2,3).
故答案为:(﹣1,﹣2,3).
11.【解答】解:空间直角坐标系中,点M(x,y,z)关于x轴的对称点坐标是M′(x,﹣y,﹣z);
所以空间直角坐标系O﹣xyz中,点A=(﹣1,1,﹣2)关于x轴的对称点坐标是:(﹣1,﹣1,2);
故答案为:(﹣1,﹣1,2).
12.【解答】解:点P(4,﹣2,3)到原点的距离为,
在空间直角坐标系中,点P(4,﹣2,3)关于z轴对称的点的坐标为:(﹣4,2,﹣3).
故答案为:,(﹣4,2,﹣3).
13.【解答】解:已知点A(2,3,4),B(3,1,1),点M在平面xOy上,由于|MA|+|MB|,
可得|MA|+|MB|的最小值即为A到点B关于平面xOy的对称点B′的距离,点M为AB′与平面xOy的交点,
因为B关于平面xOy的对称点B′的坐标为(3,1,﹣1),
即|MA|+|MB|的最小值为AB′,
故答案为:.
14.【解答】解:∵空间直角坐标系中,A(3,﹣6,0),B(7,2,z),|AB|=12,
∴12,
∴z2=64.解得z=±8.
故答案为:±8.
15.【解答】解:∵A(x,5﹣x,2x﹣1),B(1,x+2,2﹣x),
∴||,
∴当||取最小值时,x的值等于.
故答案为.
三.解答题
16.【解答】解:点A(﹣4,2,3)关于坐标原点的对称点为A1,
则A1=(4,﹣2,﹣3),
则A1关于xOz平面的对称点为A2=(4,2,﹣3),
A2关于z轴的对称点为A3=(﹣4,﹣2,﹣3),
故线段AA3的中点M的坐标为(﹣4,0,0).
17.【解答】解:设Q(x,y,z),
∵,点A(2,4,0),B(1,3,3),
∴(x﹣2,y﹣4,z)=﹣2(1﹣x,3﹣y,3﹣z),
∴,解得x=0,y=2,z=6,
∴Q(0,2,6).
18.【解答】解:由题意设P(0,y,0),因为PA=7,
所以:7,
所以y=2或y=8,
所以点P的坐标为:(0,2,0)或(0,8,0).
故答案为:(0,2,0)或(0,8,0).
19.【解答】解:(1)P1(2,﹣2,0),P2(4,0,1);
∴|P1P2|3;
(2)P1(1,﹣1,3),P2(1,2,﹣1).
∴|P1P2|5.
20.【解答】解:点P(﹣4,﹣2,3)关于坐标平面xOy及y轴的对称点的坐标分别是A和B.
∵点P(﹣4,﹣2,3)关于坐标平面xoy的对称点为(﹣4,﹣2,﹣3),
点P(﹣4,﹣2,3)关于y轴的对称点的坐标(4,﹣2,﹣3),
∴A(﹣4,﹣2,﹣3),B(4,﹣2,﹣3),
∴线段AB的长|AB|8.
21.【解答】(本小题满分13分)
解:(Ⅰ)∵正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.
以A为原点,建立如图所示的空间直角坐标系A﹣xyz.
∴A(0,0,0),B(2,0,0),C(2,2,0),
D(0,2,0),P(0,0,2),E(0,1,1).
(Ⅱ)∵(﹣2,﹣1,1),
∴||.
22.【解答】解:(1)|AB|3,同理可得|BC|=3,|AC|=3.
(2)∵|BC|2,∴∠A=90°.∠B=∠C=45°.
(3)设△ABC的重心G(x,y,z),则2,2,7.
∴G(2,﹣2,7).
23.【解答】解:如图建立空间直角坐标系,
则A(a,0,0),B(a,a,0),C(0,a,o),D(0,0,0),A1(a,0,a),B1(a,a,a),
C1(0,a,a),D1(0,0,a),P(,,).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题基础练
第四章《圆与方程》
4.3
空间直角坐标系
一.选择题
1.(2020秋?天津期末)在空间直角坐标系中,已知点A(2,﹣1,3),B(﹣4,1,﹣1),则线段AB的中点坐标是( )
A.(﹣1,0,2)
B.(﹣1,0,1)
C.(3,0,1)
D.(﹣1,1,1)
2.(2020秋?和平区校级月考)在空间直角坐标系中,已知点A(4,﹣3,5),B(﹣2,1,﹣7),则线段AB的中点坐标是( )
A.(2,﹣2,﹣2)
B.(1,﹣1,﹣1)
C.(1,1,1)
D.(2,2,2)
3.(2020秋?山东月考)点A(2,﹣1,3)关于xOy平面的对称点为( )
A.(2,﹣1,﹣3)
B.(2,1,3)
C.(﹣2,1,3)
D.(﹣2,﹣1,3)
4.(2020秋?汾阳市期中)在空间直角坐标系O﹣xyz中,点A(﹣1,0,3)关于坐标原点的对称点为B,则|AB|=( )
A.2
B.
C.
D.10
5.(2020春?荔湾区期中)在空间直角坐标系中,A(2,3,5),B(3,1,4)两点之间的距离为( )
A.
B.2
C.
D.
6.(2020秋?涪城区校级期中)空间直角坐标系中,点B(2,1,6)关于xOz平面的对称点为C,则A(﹣3,4,0)与C的距离为( )
A.2
B.2
C.
D.9
7.(2020秋?新泰市校级期中)已知A(1,﹣2,3)、B(2,1,﹣1)两点,则直线AB与空间直角坐标系中的yOz平面的交点坐标为( )
A.(0,0,0)
B.(0,﹣5,7)
C.()
D.()
二.填空题
8.(2020秋?辽阳期末)已知A(5,﹣7),B(3,﹣1),且C与A关于点B对称,则C的坐标为
.
9.(2020秋?庐阳区校级期中)在空间直角坐标系O﹣xyz中,若点A(1,2,3),B(1,﹣1,4),点C是点A关于平面yOz的对称点,则点B与C的距离为
.
10.(2020秋?黎川县校级期中)在空间直角坐标系中,点M(1,﹣2,3)关于平面yOz对称的点的坐标是
.
11.(2020秋?西城区校级期中)在空间直角坐标系中点A=(﹣1,1,﹣2)关于x轴的对称点的坐标是
.
12.(2020秋?浙江月考)在空间直角坐标系中,点P(4,﹣2,3)到原点的距离为
,关于z轴对称的点的坐标为
.
13.(2020春?越秀区期末)在空间直角坐标系中,已知点A(2,3,4),B(3,1,1),点M在平面xOy上,则|MA|+|MB|的最小值为
.
14.(2020秋?黎川县校级期中)在空间直角坐标系中,若A(3,﹣6,0),B(7,2,z),|AB|=12,则z=
.
15.(2019秋?淮南期末)若两点A(x,5﹣x,2x﹣1),B(1,x+2,2﹣x),当||取最小值时,x的值等于
.
三.解答题
16.已知点A(﹣4,2,3)关于坐标原点的对称点为A1,A1关于xOz平面的对称点为A2,A2关于z轴的对称点为A3,求线段AA3的中点M的坐标.
17.已知点A(2,4,0),B(1,3,3),在直线AB上有一点Q,使得2,求点Q的坐标.
18.已知A(2,5,﹣6),在y轴上求一点P,使PA=7.
19.分别根据下列条件,求空间两点P1,P2间的距离:
(1)P1(2,﹣2,0),P2(4,0,1);
(2)P1(1,﹣1,3),P2(1,2,﹣1).
20.(2017秋?大方县校级月考)若点P(﹣4,﹣2,3)关于坐标平面xOy及y轴的对称点的坐标分别是A和B.
求线段AB的长.
21.(2015秋?怀柔区期末)已知正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.以A为原点,建立如图所示的空间直角坐标系A﹣xyz.
(Ⅰ)求点A,B,C,D,P,E的坐标;
(Ⅱ)求.
22.(2013秋?船山区校级月考)已知△ABC的三个顶点A(1,﹣1,7),B(3,﹣2,5),C(2,﹣3,9).
(1)试求△ABC的各边之长;
(2)求三角形的三个内角的大小;
(3)写出△ABC的重心坐标.
23.(2012秋?临汾校级期中)如图,已知正方体ABCD﹣A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
参考答案与试题解析
一.选择题
1.【解答】解:因为点A(2,﹣1,3),B(﹣4,1,﹣1),
所以线段AB的中点坐标是(﹣1,0,1).
故选:B.
2.【解答】解:在空间直角坐标系中,
点A(4,﹣3,5),B(﹣2,1,﹣7),
则线段AB的中点坐标是(1,﹣1,﹣1).
故选:B.
3.【解答】解:点A(2,﹣1,3)关于xOy平面的对称点为(2,﹣1,﹣3).
故选:A.
4.【解答】解:由题意得:
点A(﹣1,0,3)关于坐标原点的对称点B(1,0,﹣3),
则|AB|2,
故选:C.
5.【解答】解:在空间直角坐标系中,A(2,3,5),B(3,1,4),
两点之间的距离为:.
故选:D.
6.【解答】解:∵空间直角坐标系中,点B(2,1,6)关于xOz平面的对称点为C,
∴点C的坐标为C(2,﹣1,6).
A(﹣3,4,0)与C的距离为:
故选:C.
7.【解答】解:设C点为(0,a,b),则由题意得,
解得a=﹣5,b=7,
所以C点坐标为(0,﹣5,7).
故选:B.
二.填空题
8.【解答】解:设C(x,y),
∵A(5,﹣7),B(3,﹣1),且C与A关于点B对称,
∴,即(﹣2,6)=(x﹣3,y+1),
∴,解得x=1,y=5.
∴C的坐标为(1,5).
故答案为:(1,5).
9.【解答】解:空间直角坐标系O﹣xyz中,点A(1,2,3),B(1,﹣1,4),
则点A关于平面yOz的对称点为C(﹣1,2,3),
所以点B与C的距离为|BC|.
故答案为:.
10.【解答】解:空间直角坐标系中,点M(1,﹣2,3)关于平面yOz对称的点的坐标是(﹣1,﹣2,3).
故答案为:(﹣1,﹣2,3).
11.【解答】解:空间直角坐标系中,点M(x,y,z)关于x轴的对称点坐标是M′(x,﹣y,﹣z);
所以空间直角坐标系O﹣xyz中,点A=(﹣1,1,﹣2)关于x轴的对称点坐标是:(﹣1,﹣1,2);
故答案为:(﹣1,﹣1,2).
12.【解答】解:点P(4,﹣2,3)到原点的距离为,
在空间直角坐标系中,点P(4,﹣2,3)关于z轴对称的点的坐标为:(﹣4,2,﹣3).
故答案为:,(﹣4,2,﹣3).
13.【解答】解:已知点A(2,3,4),B(3,1,1),点M在平面xOy上,由于|MA|+|MB|,
可得|MA|+|MB|的最小值即为A到点B关于平面xOy的对称点B′的距离,点M为AB′与平面xOy的交点,
因为B关于平面xOy的对称点B′的坐标为(3,1,﹣1),
即|MA|+|MB|的最小值为AB′,
故答案为:.
14.【解答】解:∵空间直角坐标系中,A(3,﹣6,0),B(7,2,z),|AB|=12,
∴12,
∴z2=64.解得z=±8.
故答案为:±8.
15.【解答】解:∵A(x,5﹣x,2x﹣1),B(1,x+2,2﹣x),
∴||,
∴当||取最小值时,x的值等于.
故答案为.
三.解答题
16.【解答】解:点A(﹣4,2,3)关于坐标原点的对称点为A1,
则A1=(4,﹣2,﹣3),
则A1关于xOz平面的对称点为A2=(4,2,﹣3),
A2关于z轴的对称点为A3=(﹣4,﹣2,﹣3),
故线段AA3的中点M的坐标为(﹣4,0,0).
17.【解答】解:设Q(x,y,z),
∵,点A(2,4,0),B(1,3,3),
∴(x﹣2,y﹣4,z)=﹣2(1﹣x,3﹣y,3﹣z),
∴,解得x=0,y=2,z=6,
∴Q(0,2,6).
18.【解答】解:由题意设P(0,y,0),因为PA=7,
所以:7,
所以y=2或y=8,
所以点P的坐标为:(0,2,0)或(0,8,0).
故答案为:(0,2,0)或(0,8,0).
19.【解答】解:(1)P1(2,﹣2,0),P2(4,0,1);
∴|P1P2|3;
(2)P1(1,﹣1,3),P2(1,2,﹣1).
∴|P1P2|5.
20.【解答】解:点P(﹣4,﹣2,3)关于坐标平面xOy及y轴的对称点的坐标分别是A和B.
∵点P(﹣4,﹣2,3)关于坐标平面xoy的对称点为(﹣4,﹣2,﹣3),
点P(﹣4,﹣2,3)关于y轴的对称点的坐标(4,﹣2,﹣3),
∴A(﹣4,﹣2,﹣3),B(4,﹣2,﹣3),
∴线段AB的长|AB|8.
21.【解答】(本小题满分13分)
解:(Ⅰ)∵正方形ABCD的边长为2,PA⊥平面ABCD,且PA=2,E是PD中点.
以A为原点,建立如图所示的空间直角坐标系A﹣xyz.
∴A(0,0,0),B(2,0,0),C(2,2,0),
D(0,2,0),P(0,0,2),E(0,1,1).
(Ⅱ)∵(﹣2,﹣1,1),
∴||.
22.【解答】解:(1)|AB|3,同理可得|BC|=3,|AC|=3.
(2)∵|BC|2,∴∠A=90°.∠B=∠C=45°.
(3)设△ABC的重心G(x,y,z),则2,2,7.
∴G(2,﹣2,7).
23.【解答】解:如图建立空间直角坐标系,
则A(a,0,0),B(a,a,0),C(0,a,o),D(0,0,0),A1(a,0,a),B1(a,a,a),
C1(0,a,a),D1(0,0,a),P(,,).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
