【同步必刷题】1.1 空间几何体的结构 提高练(含解析)
文档属性
| 名称 | 【同步必刷题】1.1 空间几何体的结构 提高练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:09:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题提高练
第一章《空间几何体》
1.1
空间几何体的结构
一.选择题
1.(2020秋?浙江期中)若三棱锥P﹣ABC满足,PA=BC,PB=AC,PC=AB,则该三棱锥可能是( )
A.AB=2,BC=3,CA=4
B.AB=3,BC=4,CA=5
C.AB=4,BC=5,CA=6
D.以上选项都不可能
2.(2020春?越秀区校级期中)在长方体A1B1C1D1﹣ABCD中,直线A1C与平面BC1D交于点M,则M为△BC1D的( )
A.垂心
B.内心
C.外心
D.重心
3.(2020秋?大连期中)如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,P是侧棱CC1上的一点,且CP=m(0<m<2),设λ(0≤λ≤1),D1Q在平面APD1上的正投影垂直于AP,则有( )
A.λ
B.λ
C.λ
D.λ随着m的变化而变化
4.(2020秋?湖州期中)如图,已知三棱柱ABC﹣A'B'C'的底面是正三角形,侧棱AA′⊥底面ABC,AB=9,AA'=3,点P在四边形ABB'A'内,且P到AA',A'B'的距离都等于1,若D为BC上靠近C的四等分点,过点P且与A'D平行的直线交三棱柱ABC﹣A'B'C'于点P,Q两点,则点Q所在平面是( )
A.ACC'A'
B.BCC'B'
C.ABC
D.ABB'A'
5.(2020秋?湖北期中)设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,)
B.[0,)
C.(,1)
D.(,1)
6.(2020?眉山模拟)已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面α,满足CP⊥平面α,则平面α与正方体ABCD﹣A1B1C1D1的截面周长为( )
A.4
B.12
C.8
D.8
7.(2020?大观区校级模拟)已知在三棱锥P﹣ABC中,O为AB中点,PO⊥平面ABC,∠APB=90°,PA=PB=2,下列说法中错误的是( )
A.若O为△ABC的外心,则PC=2
B.若△ABC为等边三角形,则AP⊥BC
C.当∠ACB=90°时,PC与平面PAB所成角的范围为
D.当PC=4时,M为平面PBC内动点,若OM∥平面PAC,则M在三角形PBC内的轨迹长度为2
8.(2020秋?潞州区校级期中)如图,在正四棱台ABCD﹣A1B1C1D1中,上底面边长为4,下底面边长为8,高为5,点M,N分别在A1B1,D1C1上,且A1M=D1N=1.过点M,N的平面α与此四棱台的下底面会相交,则平面α与四棱台的面的交线所围成图形的面积的最大值为( )
A.18
B.30
C.6
D.36
9.(2020?昌平区模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为3,点E在棱BC上,且满足BE=2EC,动点M在正方体表面上运动,且ME⊥BD1,则动点M的轨迹的周长为( )
A.
B.
C.
D.
二.填空题
10.(2020秋?余姚市校级月考)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,,AD=2,则四边形ABCD绕直线AD旋转一周所形成的几何体的表面积是
,体积是
.
11.(2020秋?全国月考)把圆心角为90°的扇形铁片围成一个侧面积为16πm2的圆锥(接缝处忽略不计),该圆锥竖直倒置后放入一个球,该球恰好与圆锥的侧面上边缘相切,则球心到圆锥顶点的距离为
m.
12.(2020秋?四川月考)古人为避雷和便于雨水下泄,常将屋顶设计成圆锥形状,多见于我国东南沿海地带,经测算某圆锥屋顶的轴截面为一个斜边长约为20米的等腰直角三角形,则圆锥的侧面积约为
平方米.
13.(2020?石家庄模拟)在四面体ABCD中,AC=BC=CD=8,AB=AD=BD=6,AB?平面α,E,F分别为线段AD,BC的中点,现将四面体以AB为轴旋转,则线段EF在平面内投影长度的取值范围是
.
14.(2019秋?湛江期末)已知平行六面体ABCD﹣A1B1C1D1,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,则AC1=
.
15.(2019春?福州期末)如图,在直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB=AA1=2,AD=CD=BC=1,M,N分别为CC1,DD1的中点,平面ABM∩平面A1B1C1D1=l.给出以下几个说法:
①A1B1∥l;
②直线AN与l的夹角为45°;
③l与平面BB1C1C所成的角为60°
④平面ADD1A1内存在直线与l平行.
其中正确命题的序号是
.
三.解答题
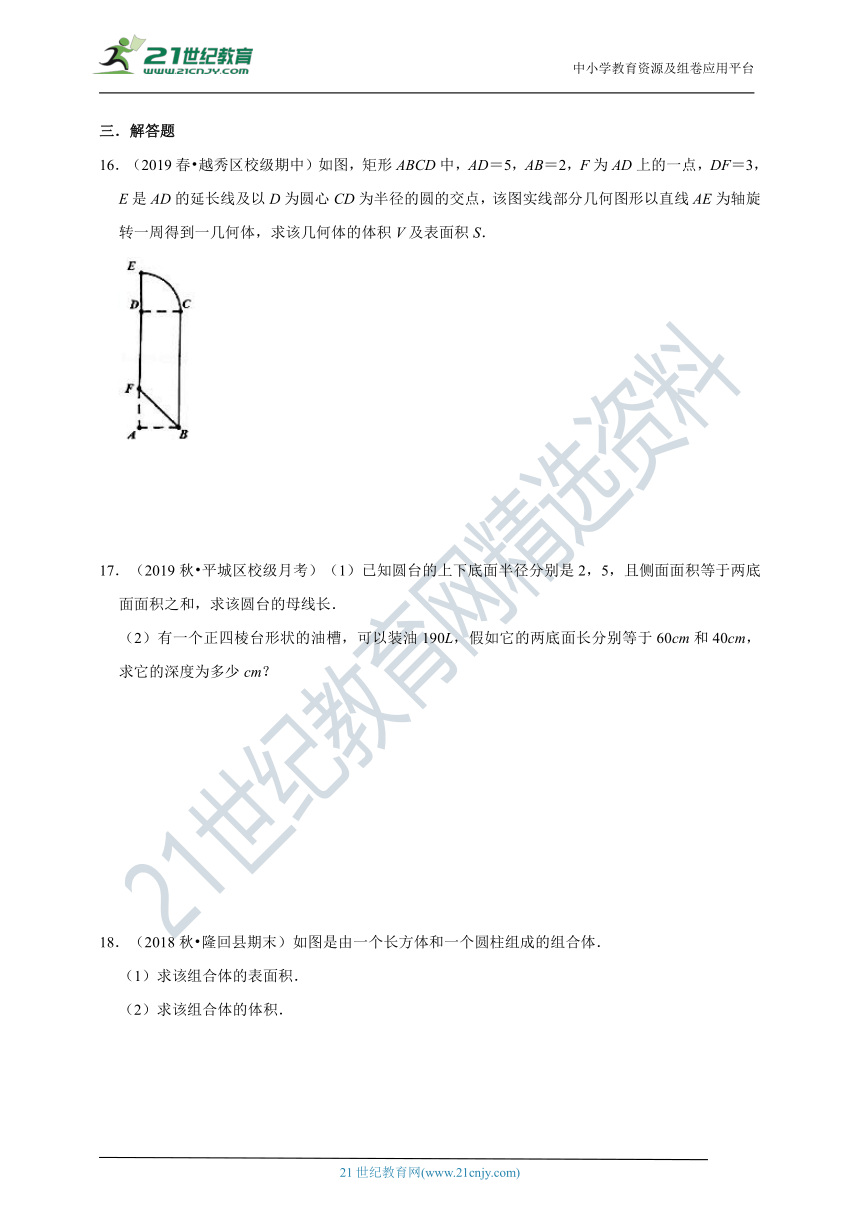
16.(2019春?越秀区校级期中)如图,矩形ABCD中,AD=5,AB=2,F为AD上的一点,DF=3,E是AD的延长线及以D为圆心CD为半径的圆的交点,该图实线部分几何图形以直线AE为轴旋转一周得到一几何体,求该几何体的体积V及表面积S.
17.(2019秋?平城区校级月考)(1)已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(2)有一个正四棱台形状的油槽,可以装油190L,假如它的两底面长分别等于60cm和40cm,求它的深度为多少cm?
18.(2018秋?隆回县期末)如图是由一个长方体和一个圆柱组成的组合体.
(1)求该组合体的表面积.
(2)求该组合体的体积.
19.(2019秋?江苏月考)某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成,它的轴截面如图所示,已知半球的直径是12cm,圆柱筒高6cm,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆AC,BD,O1C,O1D,O2A,O2B及O1O2焊接而成,其中O1,O2分别是圆柱上下底面的圆心,A,B,C,D均在“浮球”的内壁上,AC,BD通过“浮球”中心O,且AD、BC均与圆柱的底面垂直.
(1)设O1C与圆柱底面所成的角为θ,试用θ表示出防压卡中四边形O1O2BC的面积f(θ),并写出θ的取值范围;
(2)研究表明,四边形O1O2BC的面积越大,“浮球”防压性越强,求四边形O1O2BC面积取最大值时,点C到圆柱上底面的距离d.
20.(2019春?武侯区校级月考)如图,在四棱锥P﹣ABCD中,AB⊥PC,AD∥BC,AD⊥CD,且PC=BC=2AD=2CD=2,PA=2.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)在线段PD上,是否存在一点M,使得BM∥平面AMC,求的值.
21.(2018秋?湖北期末)在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,平面PAC⊥底面ABCD,PA=PC=2.
(1)求证:PB=PD;
(2)若点M,N分别是棱PA,PC的中点,平面DMN与棱PB的交点Q,
则在线段BC上是否存在一点H,使得DQ⊥PH,若存在,求BH的长,
若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:将三棱锥P﹣ABC放置入长方体中,设长方体的长、宽、高分别为a,b,c,
则AB2=b2+c2,BC2=a2+b2,AC2=a2+c2,
在△ABC中,由余弦定理知,cos∠BAC0,
∴∠BAC为锐角,
同理可得,∠ABC和∠ACB均为锐角,即△ABC为锐角三角形.
选项A,∵AB2+BC2=4+9<CA2=16,∴△ABC为钝角三角形,不符合题意;
选项B,∵AB2+BC2=9+16=CA2=25,∴△ABC为直角三角形,不符合题意;
选项C,∵AB2+BC2=16+25>CA2=36,∴△ABC为锐角三角形,符合题意.
故选:C.
2.【解答】解:连接AC,BD,设交点为O,
由平面ACC1A1∩平面BDC1=C1O,
而M∈A1C,A1C?平面AA1C1C,
又M∈平面BDC1,所以M∈C1O,
故C1,M,O三点共线,
由OC∥A1C1,
可得△OMC∽△C1MA1,
所以,
又因为OC1为△BDC1的中线,
所以M为△BDC1的重心.
故选:D.
3.【解答】解:以D为原点,DA,DC,DD1分别为x、y、z轴建立如图所示的空间直角坐标系,
则A(1,0,0),P(0,1,m),D1(0,0,2),Q(1﹣λ,λ,2),
∴(﹣1,1,m),(1﹣λ,λ,0),
∵D1Q在平面APD1上的正投影垂直于AP,
∴?(1﹣λ)+λ=0,
∴λ.
故选:B.
4.【解答】解:如图所示:
连接A′P并延长交直线AB于点M,
由于点P在四边形AA′B′B内,且点P到AA′,A′B′的距离都等于1,
可知∠AA′M=45°,则△AA′M为等腰直角三角形,且AM=AA′=3<AB,
所以,点M在线段AB上,
连接DM,由于点P在线段A′M上,过点P作PQ∥A′D交DM于点Q,
则点Q即为所求,且点Q在线段DM上,
因此点Q在平面ABC内,
故选:C.
5.【解答】解:建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,1),
由λ,可得P(λ,λ,1﹣λ),
则(1﹣λ,﹣λ,λ﹣1),(﹣λ,1﹣λ,λ﹣1),
因为∠APC为锐角,
所以(1﹣λ,﹣λ,λ﹣1)?(﹣λ,1﹣λ,λ﹣1)=(λ﹣1)(3λ﹣1)>0,解得λ,或λ>1,
又因为动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,
所以0,故λ的取值范围是[0,).
故选:A.
6.【解答】解:取
AD
中点
E,AB
中点
F,连接PD,D1E,EF,B1F,B1D1,AC,
如下图所示:
E
为
AD
中点,F
为
AB
中点,则
EF∥BD,BD∥B1D1
所以
EF∥B1D1
所以
E,F,B1,D1
四点共面.
根据正方形性质可知
CD⊥平面
ADD1A1,
而
D1E?平面ADD1A1,所以
CD⊥D1E,
A△D1DE≌△DAP,可知∠ED1D=∠PDA,
而∠PDA+∠PDD1=90°,所以∠ED1D+∠PDD1=90°,
即
PD⊥D1E
为为
CD∩PD=D,所以
D1E⊥平面
PDC,
而CP?平面
PDC,所以
D1E⊥CP;
E
为
AD
中点,F
为
AB
中点,由正方形和正方体性质可知
EF⊥AC,PA⊥EF,且
PA∩AC=A,
所以
EF⊥平面
PAC,而
CP?平面
PDC,
所以
EF⊥CP,又因为
D1E⊥CP,D1E∩EF=E
所以
CP⊥平面
EFB1D1
即平面
EFB1D1
为平面
与正方体
ABCD﹣A1B1C1D1
的截面,
正方体
ABCD﹣A1B1C1D1
棱长为
4
所以
EFB1D1
的周长为
B1D1+D1E+EF+B1F
,
故选:A.
7.【解答】解:O为△ABC的外心,可得OA=OB=OC,
PO⊥平面ABC,可得PO⊥OC,即有PC2,A正确;
若△ABC为等边三角形,若AP⊥BC,又AP⊥PB,可得AP⊥平面PBC,
即AP⊥PC,由PO⊥OC可得PC2AC,矛盾,
故B错误;
若∠ACB=90°时,设PC与平面PAB所成角为θ,
可得OC=OA=OB,PC=2,设C到平面PAB的距离为d,
由VC﹣PAB=VP﹣ABC,可得d??2?2??AC?BC,
即有AC?BC=2d4,当且仅当AC=BC=2取得等号,
可得d的最大值为,sinθ,即有θ的范围为(0,],C正确;
取BC的中点N,PB的中点K,连接OK,ON,KN,
由中位线定理可得ON∥AC,OK∥PA,可得平面OKN∥平面PAC,
可得M在线段KN上,而KNPC=2,可得D正确.
故选:B.
8.【解答】解:依题意,平面α与四棱台的面的交线所围成图形为以MN为上底,以在底面ABCD内且与MN平行的线段为下底的梯形,
即该梯形的上底长为4,下底长为8,所以当梯形的高最大时,平面α与四棱台的面的交线所围成图形的面积的最大值,即当该梯形为MNCB时面积最大.
过M做ME⊥平面ABCD,过点E做EG垂直于BC于G,交AD于F,
则因为BC?平面ABCD,所以BC⊥ME,又因为BC⊥EG,EG∩ME=E,
所以BC⊥平面MEG,
因为MG?平面MEG,
所以MG⊥BC.
所以,在平面A1B1GF中,做A1H⊥FG=H,B1I⊥FG=I,
则FH=IG2,HE=A1M=1,
所以EG=AB﹣FE=8﹣3=5,又因为HE=5,所以在直角三角形MEG中,MG5.
所以平面α与四棱台的面的交线所围成图形的面积的最大值为SMNCB30.
故选:B.
9.【解答】解:由正方体的特点可知BD1⊥平面ACB1,
在AB,BB1上分别取点P,Q,使得BP=2PA,BQ=2QB1,
连接PE,PQ,EQ,则PE∥AC,EQ∥B1C,
∴平面AB1C∥平面PEQ,
∴BD1⊥平面PEQ,
∴M的轨迹为△PEQ.
∵正方体棱长为3,∴AC=3,
∴PE2,
∴△PEQ的周长为3PE=6.
故选:A.
二.填空题
10.【解答】解:如图所示:
过点C作CE⊥AD,交AD的延长线于E,
由已知∠ADC=135°,所以∠CDE=45°,
所以CE=DE,
所以AE=AD+DE=4,BC,
所以四边形ABCD旋转所得的旋转体是一个组合体:
以CE=2,AB=5分别为上,下底的圆台,高AE=4,在上底挖去底面半径和高都是2的圆锥,
所以S表=S台下底+S台侧+S锥侧4(π,
体积为V,
故答案为:4()π;.
11.【解答】解:设圆锥底面半径为r
m,母线长为l
m,其轴截面如图所示:
根据题意以及弧长公式可知,,解得l=4r,
所以该圆锥的侧面积为S=πrl=4πr2=16π,解得r=2,l=8,
设母线与高的夹角为θ,则,解得cosθ,
所以球心到圆锥顶点的距离为(m).
故答案为:.
12.【解答】解:依题意,圆锥的底面半径为10米,母线长为米,
于是其侧面积为(平方米).
故答案为:.
13.【解答】解:如图,取AB的中点O,连接CO,DO,
由AC=BC,可得CO⊥AB,由AD=BD,可得DO⊥AB,
又CO∩DO=O,∴AB⊥平面CDO,得AB⊥CD.
取AC中点为G,连接EG、FG,
∵E,F分别是线段AD和BC的中点,∴GF∥AB,GE∥CD,
∴GE⊥GF,
∴EF2=GE2+GF2=()2+()2=16+9=25,
当四面体绕AB旋转时,
∵GF∥平面α,GE与GF的垂直性保持不变,
当CD与平面α垂直时,EF在平面上的射影长最短为GF=3;
当CD与平面α平行时,平面EFG∥平面α,此时EF在平面α上的射影最长为EF,
∴线段EF在平面α上的射影长的取值范围是[3,5].
故答案为:[3,5].
14.【解答】解:∵AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,
∴,
∵,
∴2226,
∴||.
故答案为:.
15.【解答】解:在直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB=AA1=2,AD=CD=BC=1,
M,N分别为CC1,DD1的中点,平面ABM∩平面A1B1C1D1=l.
在①中,∵在直四棱柱ABCD﹣A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
平面ABM∩平面A1B1C1D1=l,平面ABM∩平面ABCD=AB,A1B1∥AB,
∴A1B1∥l,故①正确;
在②中,取AB中点E,连结DE、NE,则AD=AE=DE=DN=1,
NE=AN,
cos∠EAN,
∵l∥A1B1,A1B1∥AB,∴l∥AB,
∴直线AN与l所成角为∠NAE=arccos,故②错误;
在③中,l与平面BB1C1C所成的角即为AB与平面BB1C1C所成的角,
取AD中点O,则EO⊥AD,AA1⊥EO,
∵AD∩AA1=A,∴EO⊥平面ADD1A1,
∴∠EAO=60°就是l与平面BB1C1C所成的角,故③正确;
在④中,∵l∥AB,AB∩平面ADD1A1=A,
∴平面ADD1A1内不存在直线与l平行,故④错误.
故选:①③.
三.解答题
16.【解答】解:直线AE为轴旋转一周得到一几何体,其上部是一个半球体,球的半径CD=2,
下部为一个以CD=2为半径,高AD=5的圆柱体,然后挖掉一个底面半径为AB=2,高为AF=AD﹣DF=3的圆锥体,
则体积为V23+π×22×5π×22×3,
S4π×22+2π×2×5+π×2×3=34π.
17.【解答】解:设圆台的母线长为l,
则圆台的上底面面积为S上=π?22=4π,
圆台的下底面面积为S下=π?52=25π,
所以圆台的底面面积为S=S上+S下=29π,
又圆台的侧面积S侧=π(2+5)l=7πl,
于是7πl=29π,即l;
(2)由于V(SS′)h,
则h75cm.
故它的深度为75cm.
18.【解答】解:(1)该组合体的表面积为
S组合体=S长方体+S圆柱侧=2×(8×8+4×8+4×8)+2π×2×8=256+32π;
(2)该组合体的体积为
V组合体=V长方体+V圆柱=4×8×8+π×22×8=256+32π.
19.【解答】解:(1)因为O1、O2分别是圆柱上、下底面的圆心,所以O1O2与圆柱的底面垂直;
因为BC与圆柱的底面垂直,所以O1O2∥BC;
在梯形O1O2BC中,O1O2=6,BC=12sinθ+6,O1H=6cosθ;
所以梯形O1O2BC的面积为
f(θ)(O1O2+BC)×O1H[6+(12sinθ+6)]×6cosθ=36sinθcosθ+36cosθ,
其中θ的取值范围是(0,);
(2)由(1)得,f′(θ)=﹣36(2sin2θ+sinθ﹣1)=﹣36(2sinθ﹣1)(sinθ+1),
令f′(θ)=0,解得sinθ或sinθ=﹣1(不合题意,舍去);
又θ∈(0,),所以θ;
列表如下;
θ
(0,)
(,)
f'(θ)
+
0
﹣
f(θ)
单调增
极大值
单调减
所以当θ时,f(θ)取得极大值,即是最大值,此时d=6sinθ=63;
所以四边形O1O2BC面积取最大值时,点C到圆柱上底面的距离为d=3cm.
20.【解答】证明:(Ⅰ)∵在底面ABCD中,AD∥BC,AD⊥CD,
且BC=2AD=2CD=2,
∴AB=AC=2,BC=2,
∴AB⊥AC,
又∵AB⊥PC,AC∩PC=C,AC?平面PAC,PC?平面PAC,
∴AB⊥平面PAC,
∴AB⊥PA,
∵PA=AC=2,PC=2,
∴PA⊥AC,
又∵PA⊥AB,AB∩AC=A,AB?平面ABCD,AC?平面ABCD,
∴PA⊥平面ABCD.
解:(2)以A为原点,AB,AC,AP所成角分别为x,y,z轴,建立空间直角坐标系,
A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣1,1,0),
设M(a,b,c),,λ∈[0,1],
则(a,b,c﹣2)=(﹣λ,λ,﹣2λ),∴M(﹣λ,λ,2﹣2λ),
(﹣λ﹣2,λ,2﹣2λ),(﹣λ,λ,2﹣2λ),(0,2,0),
设平面AMC的法向量(x,y,z),
则,取x=1,得(1,0,),
∵BM∥平面AMC,∴λ﹣2+(2﹣2λ)?0,方程无解,
∴在线段PD上,不存在一点M,使得BM∥平面AMC.
21.【解答】(1)证明:记AC∩BD=O,连结PO,
∵底面ABCD为正方形,∴OA=OC=OB=OD=2.
∵PA=PC,∴PO⊥AC,
∵平面PAC∩底面ABCD=AC,PO?平面PAC,
∴PO⊥底面ABCD.
∵BD?底面ABCD,∴PO⊥BD.
∴PB=PD;
(2)解:以O为坐标原点,射线OB,OC,OP的方向分别为x,y,z轴的正方向建立空间直角坐标系如图所示,
由(1)可知OP=2.
可得P(0,0,2),A(0,﹣2,0),B(2,0,0),C(0,2,0),D(﹣2,0,0),
可得,M(0,﹣1,1),N(0,1,1).
,.
设平面DMN的法向量,
由,令x=1,可得.
记,可得Q(2λ,0,2﹣2λ),
,
由,可得,2λ+2﹣4+4λ=0,解得.
可得,.
记,可得H(2﹣2t,2t,0),
,若DQ⊥PH,则,
∴,解得t.
故BH.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题提高练
第一章《空间几何体》
1.1
空间几何体的结构
一.选择题
1.(2020秋?浙江期中)若三棱锥P﹣ABC满足,PA=BC,PB=AC,PC=AB,则该三棱锥可能是( )
A.AB=2,BC=3,CA=4
B.AB=3,BC=4,CA=5
C.AB=4,BC=5,CA=6
D.以上选项都不可能
2.(2020春?越秀区校级期中)在长方体A1B1C1D1﹣ABCD中,直线A1C与平面BC1D交于点M,则M为△BC1D的( )
A.垂心
B.内心
C.外心
D.重心
3.(2020秋?大连期中)如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=2,P是侧棱CC1上的一点,且CP=m(0<m<2),设λ(0≤λ≤1),D1Q在平面APD1上的正投影垂直于AP,则有( )
A.λ
B.λ
C.λ
D.λ随着m的变化而变化
4.(2020秋?湖州期中)如图,已知三棱柱ABC﹣A'B'C'的底面是正三角形,侧棱AA′⊥底面ABC,AB=9,AA'=3,点P在四边形ABB'A'内,且P到AA',A'B'的距离都等于1,若D为BC上靠近C的四等分点,过点P且与A'D平行的直线交三棱柱ABC﹣A'B'C'于点P,Q两点,则点Q所在平面是( )
A.ACC'A'
B.BCC'B'
C.ABC
D.ABB'A'
5.(2020秋?湖北期中)设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,)
B.[0,)
C.(,1)
D.(,1)
6.(2020?眉山模拟)已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面α,满足CP⊥平面α,则平面α与正方体ABCD﹣A1B1C1D1的截面周长为( )
A.4
B.12
C.8
D.8
7.(2020?大观区校级模拟)已知在三棱锥P﹣ABC中,O为AB中点,PO⊥平面ABC,∠APB=90°,PA=PB=2,下列说法中错误的是( )
A.若O为△ABC的外心,则PC=2
B.若△ABC为等边三角形,则AP⊥BC
C.当∠ACB=90°时,PC与平面PAB所成角的范围为
D.当PC=4时,M为平面PBC内动点,若OM∥平面PAC,则M在三角形PBC内的轨迹长度为2
8.(2020秋?潞州区校级期中)如图,在正四棱台ABCD﹣A1B1C1D1中,上底面边长为4,下底面边长为8,高为5,点M,N分别在A1B1,D1C1上,且A1M=D1N=1.过点M,N的平面α与此四棱台的下底面会相交,则平面α与四棱台的面的交线所围成图形的面积的最大值为( )
A.18
B.30
C.6
D.36
9.(2020?昌平区模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为3,点E在棱BC上,且满足BE=2EC,动点M在正方体表面上运动,且ME⊥BD1,则动点M的轨迹的周长为( )
A.
B.
C.
D.
二.填空题
10.(2020秋?余姚市校级月考)如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,,AD=2,则四边形ABCD绕直线AD旋转一周所形成的几何体的表面积是
,体积是
.
11.(2020秋?全国月考)把圆心角为90°的扇形铁片围成一个侧面积为16πm2的圆锥(接缝处忽略不计),该圆锥竖直倒置后放入一个球,该球恰好与圆锥的侧面上边缘相切,则球心到圆锥顶点的距离为
m.
12.(2020秋?四川月考)古人为避雷和便于雨水下泄,常将屋顶设计成圆锥形状,多见于我国东南沿海地带,经测算某圆锥屋顶的轴截面为一个斜边长约为20米的等腰直角三角形,则圆锥的侧面积约为
平方米.
13.(2020?石家庄模拟)在四面体ABCD中,AC=BC=CD=8,AB=AD=BD=6,AB?平面α,E,F分别为线段AD,BC的中点,现将四面体以AB为轴旋转,则线段EF在平面内投影长度的取值范围是
.
14.(2019秋?湛江期末)已知平行六面体ABCD﹣A1B1C1D1,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,则AC1=
.
15.(2019春?福州期末)如图,在直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB=AA1=2,AD=CD=BC=1,M,N分别为CC1,DD1的中点,平面ABM∩平面A1B1C1D1=l.给出以下几个说法:
①A1B1∥l;
②直线AN与l的夹角为45°;
③l与平面BB1C1C所成的角为60°
④平面ADD1A1内存在直线与l平行.
其中正确命题的序号是
.
三.解答题
16.(2019春?越秀区校级期中)如图,矩形ABCD中,AD=5,AB=2,F为AD上的一点,DF=3,E是AD的延长线及以D为圆心CD为半径的圆的交点,该图实线部分几何图形以直线AE为轴旋转一周得到一几何体,求该几何体的体积V及表面积S.
17.(2019秋?平城区校级月考)(1)已知圆台的上下底面半径分别是2,5,且侧面面积等于两底面面积之和,求该圆台的母线长.
(2)有一个正四棱台形状的油槽,可以装油190L,假如它的两底面长分别等于60cm和40cm,求它的深度为多少cm?
18.(2018秋?隆回县期末)如图是由一个长方体和一个圆柱组成的组合体.
(1)求该组合体的表面积.
(2)求该组合体的体积.
19.(2019秋?江苏月考)某种水箱用的“浮球”是由两个相同半球和一个圆柱筒组成,它的轴截面如图所示,已知半球的直径是12cm,圆柱筒高6cm,为增强该“浮球”的牢固性,给“浮球”内置一“双蝶形”防压卡,防压卡由金属材料杆AC,BD,O1C,O1D,O2A,O2B及O1O2焊接而成,其中O1,O2分别是圆柱上下底面的圆心,A,B,C,D均在“浮球”的内壁上,AC,BD通过“浮球”中心O,且AD、BC均与圆柱的底面垂直.
(1)设O1C与圆柱底面所成的角为θ,试用θ表示出防压卡中四边形O1O2BC的面积f(θ),并写出θ的取值范围;
(2)研究表明,四边形O1O2BC的面积越大,“浮球”防压性越强,求四边形O1O2BC面积取最大值时,点C到圆柱上底面的距离d.
20.(2019春?武侯区校级月考)如图,在四棱锥P﹣ABCD中,AB⊥PC,AD∥BC,AD⊥CD,且PC=BC=2AD=2CD=2,PA=2.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)在线段PD上,是否存在一点M,使得BM∥平面AMC,求的值.
21.(2018秋?湖北期末)在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,平面PAC⊥底面ABCD,PA=PC=2.
(1)求证:PB=PD;
(2)若点M,N分别是棱PA,PC的中点,平面DMN与棱PB的交点Q,
则在线段BC上是否存在一点H,使得DQ⊥PH,若存在,求BH的长,
若不存在,请说明理由.
参考答案与试题解析
一.选择题
1.【解答】解:将三棱锥P﹣ABC放置入长方体中,设长方体的长、宽、高分别为a,b,c,
则AB2=b2+c2,BC2=a2+b2,AC2=a2+c2,
在△ABC中,由余弦定理知,cos∠BAC0,
∴∠BAC为锐角,
同理可得,∠ABC和∠ACB均为锐角,即△ABC为锐角三角形.
选项A,∵AB2+BC2=4+9<CA2=16,∴△ABC为钝角三角形,不符合题意;
选项B,∵AB2+BC2=9+16=CA2=25,∴△ABC为直角三角形,不符合题意;
选项C,∵AB2+BC2=16+25>CA2=36,∴△ABC为锐角三角形,符合题意.
故选:C.
2.【解答】解:连接AC,BD,设交点为O,
由平面ACC1A1∩平面BDC1=C1O,
而M∈A1C,A1C?平面AA1C1C,
又M∈平面BDC1,所以M∈C1O,
故C1,M,O三点共线,
由OC∥A1C1,
可得△OMC∽△C1MA1,
所以,
又因为OC1为△BDC1的中线,
所以M为△BDC1的重心.
故选:D.
3.【解答】解:以D为原点,DA,DC,DD1分别为x、y、z轴建立如图所示的空间直角坐标系,
则A(1,0,0),P(0,1,m),D1(0,0,2),Q(1﹣λ,λ,2),
∴(﹣1,1,m),(1﹣λ,λ,0),
∵D1Q在平面APD1上的正投影垂直于AP,
∴?(1﹣λ)+λ=0,
∴λ.
故选:B.
4.【解答】解:如图所示:
连接A′P并延长交直线AB于点M,
由于点P在四边形AA′B′B内,且点P到AA′,A′B′的距离都等于1,
可知∠AA′M=45°,则△AA′M为等腰直角三角形,且AM=AA′=3<AB,
所以,点M在线段AB上,
连接DM,由于点P在线段A′M上,过点P作PQ∥A′D交DM于点Q,
则点Q即为所求,且点Q在线段DM上,
因此点Q在平面ABC内,
故选:C.
5.【解答】解:建立如图所示的空间直角坐标系,
则A(1,0,0),C(0,1,0),B(1,1,0),D1(0,0,1),
由λ,可得P(λ,λ,1﹣λ),
则(1﹣λ,﹣λ,λ﹣1),(﹣λ,1﹣λ,λ﹣1),
因为∠APC为锐角,
所以(1﹣λ,﹣λ,λ﹣1)?(﹣λ,1﹣λ,λ﹣1)=(λ﹣1)(3λ﹣1)>0,解得λ,或λ>1,
又因为动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,
所以0,故λ的取值范围是[0,).
故选:A.
6.【解答】解:取
AD
中点
E,AB
中点
F,连接PD,D1E,EF,B1F,B1D1,AC,
如下图所示:
E
为
AD
中点,F
为
AB
中点,则
EF∥BD,BD∥B1D1
所以
EF∥B1D1
所以
E,F,B1,D1
四点共面.
根据正方形性质可知
CD⊥平面
ADD1A1,
而
D1E?平面ADD1A1,所以
CD⊥D1E,
A△D1DE≌△DAP,可知∠ED1D=∠PDA,
而∠PDA+∠PDD1=90°,所以∠ED1D+∠PDD1=90°,
即
PD⊥D1E
为为
CD∩PD=D,所以
D1E⊥平面
PDC,
而CP?平面
PDC,所以
D1E⊥CP;
E
为
AD
中点,F
为
AB
中点,由正方形和正方体性质可知
EF⊥AC,PA⊥EF,且
PA∩AC=A,
所以
EF⊥平面
PAC,而
CP?平面
PDC,
所以
EF⊥CP,又因为
D1E⊥CP,D1E∩EF=E
所以
CP⊥平面
EFB1D1
即平面
EFB1D1
为平面
与正方体
ABCD﹣A1B1C1D1
的截面,
正方体
ABCD﹣A1B1C1D1
棱长为
4
所以
EFB1D1
的周长为
B1D1+D1E+EF+B1F
,
故选:A.
7.【解答】解:O为△ABC的外心,可得OA=OB=OC,
PO⊥平面ABC,可得PO⊥OC,即有PC2,A正确;
若△ABC为等边三角形,若AP⊥BC,又AP⊥PB,可得AP⊥平面PBC,
即AP⊥PC,由PO⊥OC可得PC2AC,矛盾,
故B错误;
若∠ACB=90°时,设PC与平面PAB所成角为θ,
可得OC=OA=OB,PC=2,设C到平面PAB的距离为d,
由VC﹣PAB=VP﹣ABC,可得d??2?2??AC?BC,
即有AC?BC=2d4,当且仅当AC=BC=2取得等号,
可得d的最大值为,sinθ,即有θ的范围为(0,],C正确;
取BC的中点N,PB的中点K,连接OK,ON,KN,
由中位线定理可得ON∥AC,OK∥PA,可得平面OKN∥平面PAC,
可得M在线段KN上,而KNPC=2,可得D正确.
故选:B.
8.【解答】解:依题意,平面α与四棱台的面的交线所围成图形为以MN为上底,以在底面ABCD内且与MN平行的线段为下底的梯形,
即该梯形的上底长为4,下底长为8,所以当梯形的高最大时,平面α与四棱台的面的交线所围成图形的面积的最大值,即当该梯形为MNCB时面积最大.
过M做ME⊥平面ABCD,过点E做EG垂直于BC于G,交AD于F,
则因为BC?平面ABCD,所以BC⊥ME,又因为BC⊥EG,EG∩ME=E,
所以BC⊥平面MEG,
因为MG?平面MEG,
所以MG⊥BC.
所以,在平面A1B1GF中,做A1H⊥FG=H,B1I⊥FG=I,
则FH=IG2,HE=A1M=1,
所以EG=AB﹣FE=8﹣3=5,又因为HE=5,所以在直角三角形MEG中,MG5.
所以平面α与四棱台的面的交线所围成图形的面积的最大值为SMNCB30.
故选:B.
9.【解答】解:由正方体的特点可知BD1⊥平面ACB1,
在AB,BB1上分别取点P,Q,使得BP=2PA,BQ=2QB1,
连接PE,PQ,EQ,则PE∥AC,EQ∥B1C,
∴平面AB1C∥平面PEQ,
∴BD1⊥平面PEQ,
∴M的轨迹为△PEQ.
∵正方体棱长为3,∴AC=3,
∴PE2,
∴△PEQ的周长为3PE=6.
故选:A.
二.填空题
10.【解答】解:如图所示:
过点C作CE⊥AD,交AD的延长线于E,
由已知∠ADC=135°,所以∠CDE=45°,
所以CE=DE,
所以AE=AD+DE=4,BC,
所以四边形ABCD旋转所得的旋转体是一个组合体:
以CE=2,AB=5分别为上,下底的圆台,高AE=4,在上底挖去底面半径和高都是2的圆锥,
所以S表=S台下底+S台侧+S锥侧4(π,
体积为V,
故答案为:4()π;.
11.【解答】解:设圆锥底面半径为r
m,母线长为l
m,其轴截面如图所示:
根据题意以及弧长公式可知,,解得l=4r,
所以该圆锥的侧面积为S=πrl=4πr2=16π,解得r=2,l=8,
设母线与高的夹角为θ,则,解得cosθ,
所以球心到圆锥顶点的距离为(m).
故答案为:.
12.【解答】解:依题意,圆锥的底面半径为10米,母线长为米,
于是其侧面积为(平方米).
故答案为:.
13.【解答】解:如图,取AB的中点O,连接CO,DO,
由AC=BC,可得CO⊥AB,由AD=BD,可得DO⊥AB,
又CO∩DO=O,∴AB⊥平面CDO,得AB⊥CD.
取AC中点为G,连接EG、FG,
∵E,F分别是线段AD和BC的中点,∴GF∥AB,GE∥CD,
∴GE⊥GF,
∴EF2=GE2+GF2=()2+()2=16+9=25,
当四面体绕AB旋转时,
∵GF∥平面α,GE与GF的垂直性保持不变,
当CD与平面α垂直时,EF在平面上的射影长最短为GF=3;
当CD与平面α平行时,平面EFG∥平面α,此时EF在平面α上的射影最长为EF,
∴线段EF在平面α上的射影长的取值范围是[3,5].
故答案为:[3,5].
14.【解答】解:∵AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°,
∴,
∵,
∴2226,
∴||.
故答案为:.
15.【解答】解:在直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB=AA1=2,AD=CD=BC=1,
M,N分别为CC1,DD1的中点,平面ABM∩平面A1B1C1D1=l.
在①中,∵在直四棱柱ABCD﹣A1B1C1D1中,平面ABCD∥平面A1B1C1D1,
平面ABM∩平面A1B1C1D1=l,平面ABM∩平面ABCD=AB,A1B1∥AB,
∴A1B1∥l,故①正确;
在②中,取AB中点E,连结DE、NE,则AD=AE=DE=DN=1,
NE=AN,
cos∠EAN,
∵l∥A1B1,A1B1∥AB,∴l∥AB,
∴直线AN与l所成角为∠NAE=arccos,故②错误;
在③中,l与平面BB1C1C所成的角即为AB与平面BB1C1C所成的角,
取AD中点O,则EO⊥AD,AA1⊥EO,
∵AD∩AA1=A,∴EO⊥平面ADD1A1,
∴∠EAO=60°就是l与平面BB1C1C所成的角,故③正确;
在④中,∵l∥AB,AB∩平面ADD1A1=A,
∴平面ADD1A1内不存在直线与l平行,故④错误.
故选:①③.
三.解答题
16.【解答】解:直线AE为轴旋转一周得到一几何体,其上部是一个半球体,球的半径CD=2,
下部为一个以CD=2为半径,高AD=5的圆柱体,然后挖掉一个底面半径为AB=2,高为AF=AD﹣DF=3的圆锥体,
则体积为V23+π×22×5π×22×3,
S4π×22+2π×2×5+π×2×3=34π.
17.【解答】解:设圆台的母线长为l,
则圆台的上底面面积为S上=π?22=4π,
圆台的下底面面积为S下=π?52=25π,
所以圆台的底面面积为S=S上+S下=29π,
又圆台的侧面积S侧=π(2+5)l=7πl,
于是7πl=29π,即l;
(2)由于V(SS′)h,
则h75cm.
故它的深度为75cm.
18.【解答】解:(1)该组合体的表面积为
S组合体=S长方体+S圆柱侧=2×(8×8+4×8+4×8)+2π×2×8=256+32π;
(2)该组合体的体积为
V组合体=V长方体+V圆柱=4×8×8+π×22×8=256+32π.
19.【解答】解:(1)因为O1、O2分别是圆柱上、下底面的圆心,所以O1O2与圆柱的底面垂直;
因为BC与圆柱的底面垂直,所以O1O2∥BC;
在梯形O1O2BC中,O1O2=6,BC=12sinθ+6,O1H=6cosθ;
所以梯形O1O2BC的面积为
f(θ)(O1O2+BC)×O1H[6+(12sinθ+6)]×6cosθ=36sinθcosθ+36cosθ,
其中θ的取值范围是(0,);
(2)由(1)得,f′(θ)=﹣36(2sin2θ+sinθ﹣1)=﹣36(2sinθ﹣1)(sinθ+1),
令f′(θ)=0,解得sinθ或sinθ=﹣1(不合题意,舍去);
又θ∈(0,),所以θ;
列表如下;
θ
(0,)
(,)
f'(θ)
+
0
﹣
f(θ)
单调增
极大值
单调减
所以当θ时,f(θ)取得极大值,即是最大值,此时d=6sinθ=63;
所以四边形O1O2BC面积取最大值时,点C到圆柱上底面的距离为d=3cm.
20.【解答】证明:(Ⅰ)∵在底面ABCD中,AD∥BC,AD⊥CD,
且BC=2AD=2CD=2,
∴AB=AC=2,BC=2,
∴AB⊥AC,
又∵AB⊥PC,AC∩PC=C,AC?平面PAC,PC?平面PAC,
∴AB⊥平面PAC,
∴AB⊥PA,
∵PA=AC=2,PC=2,
∴PA⊥AC,
又∵PA⊥AB,AB∩AC=A,AB?平面ABCD,AC?平面ABCD,
∴PA⊥平面ABCD.
解:(2)以A为原点,AB,AC,AP所成角分别为x,y,z轴,建立空间直角坐标系,
A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣1,1,0),
设M(a,b,c),,λ∈[0,1],
则(a,b,c﹣2)=(﹣λ,λ,﹣2λ),∴M(﹣λ,λ,2﹣2λ),
(﹣λ﹣2,λ,2﹣2λ),(﹣λ,λ,2﹣2λ),(0,2,0),
设平面AMC的法向量(x,y,z),
则,取x=1,得(1,0,),
∵BM∥平面AMC,∴λ﹣2+(2﹣2λ)?0,方程无解,
∴在线段PD上,不存在一点M,使得BM∥平面AMC.
21.【解答】(1)证明:记AC∩BD=O,连结PO,
∵底面ABCD为正方形,∴OA=OC=OB=OD=2.
∵PA=PC,∴PO⊥AC,
∵平面PAC∩底面ABCD=AC,PO?平面PAC,
∴PO⊥底面ABCD.
∵BD?底面ABCD,∴PO⊥BD.
∴PB=PD;
(2)解:以O为坐标原点,射线OB,OC,OP的方向分别为x,y,z轴的正方向建立空间直角坐标系如图所示,
由(1)可知OP=2.
可得P(0,0,2),A(0,﹣2,0),B(2,0,0),C(0,2,0),D(﹣2,0,0),
可得,M(0,﹣1,1),N(0,1,1).
,.
设平面DMN的法向量,
由,令x=1,可得.
记,可得Q(2λ,0,2﹣2λ),
,
由,可得,2λ+2﹣4+4λ=0,解得.
可得,.
记,可得H(2﹣2t,2t,0),
,若DQ⊥PH,则,
∴,解得t.
故BH.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
