【同步必刷题】1.2 空间几何体的三视图和直观图 基础练(含解析)
文档属性
| 名称 | 【同步必刷题】1.2 空间几何体的三视图和直观图 基础练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:39:32 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题基础练
第一章《空间几何体》
1.2
空间几何体的三视图和直观图
一.选择题
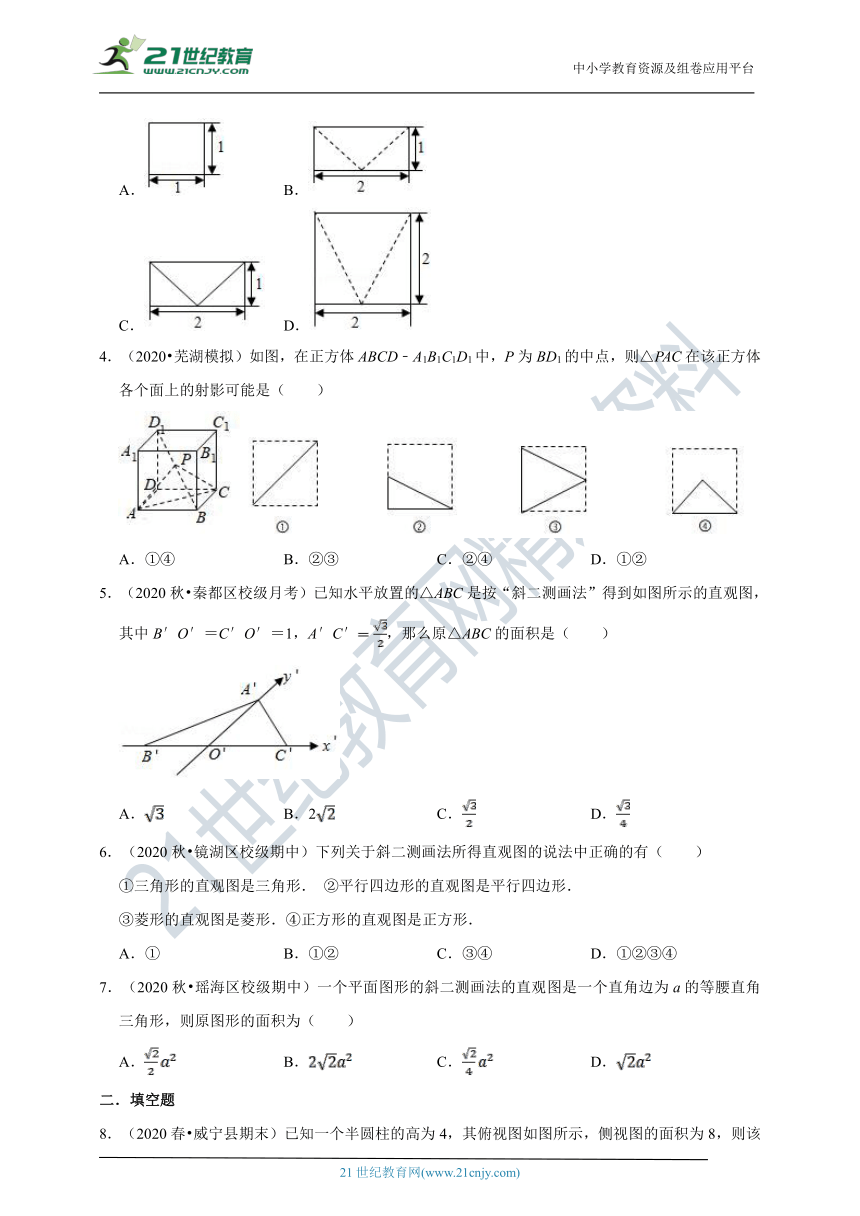
1.(2020春?雨花区校级月考)一个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为( )
A.
B.
C.
D.
2.(2020秋?龙凤区校级期末)《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(网格纸上小正方形的边长为1),则该“阳马”最长的棱长为( )
A.5
B.
C.
D.
3.(2020秋?榆林期末)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A.
B.
C.
D.
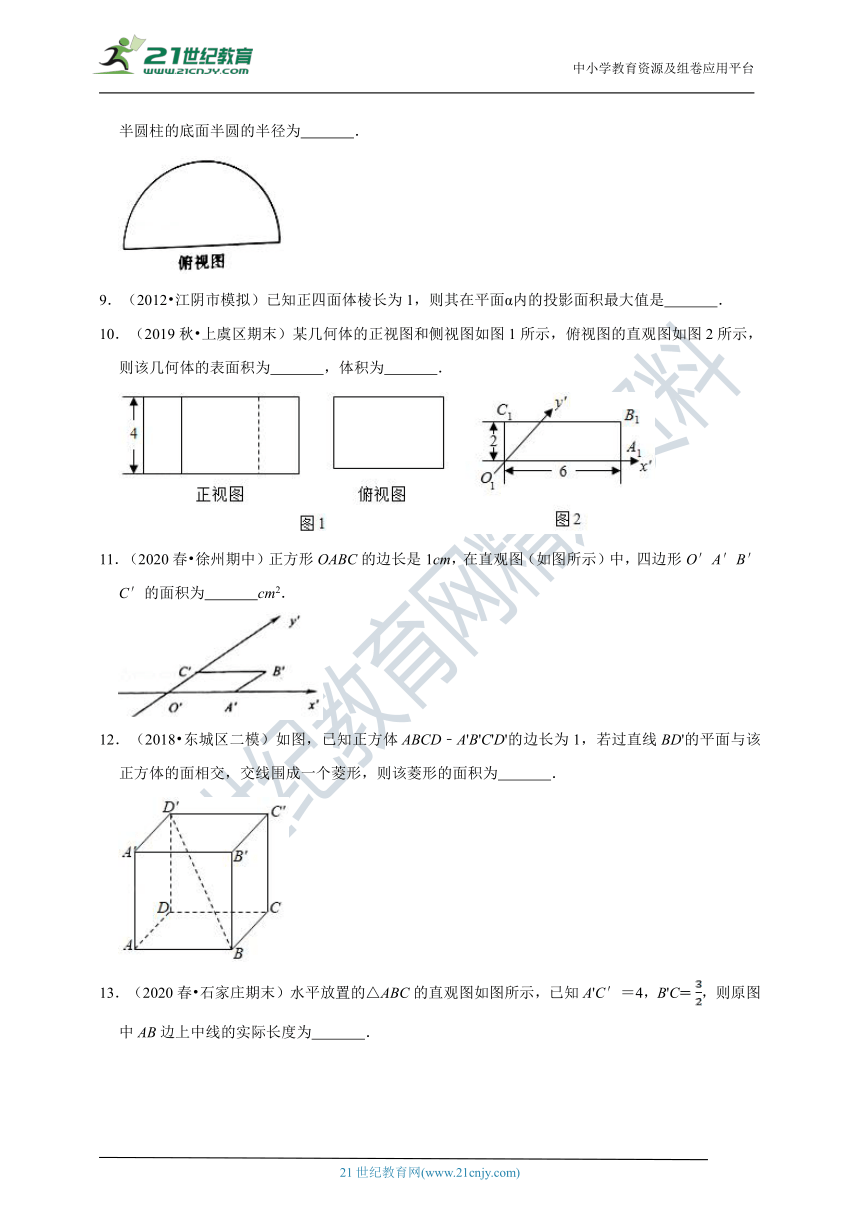
4.(2020?芜湖模拟)如图,在正方体ABCD﹣A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是( )
A.①④
B.②③
C.②④
D.①②
5.(2020秋?秦都区校级月考)已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′C′,那么原△ABC的面积是( )
A.
B.2
C.
D.
6.(2020秋?镜湖区校级期中)下列关于斜二测画法所得直观图的说法中正确的有( )
①三角形的直观图是三角形.
②平行四边形的直观图是平行四边形.
③菱形的直观图是菱形.④正方形的直观图是正方形.
A.①
B.①②
C.③④
D.①②③④
7.(2020秋?瑶海区校级期中)一个平面图形的斜二测画法的直观图是一个直角边为a的等腰直角三角形,则原图形的面积为( )
A.
B.
C.
D.
二.填空题
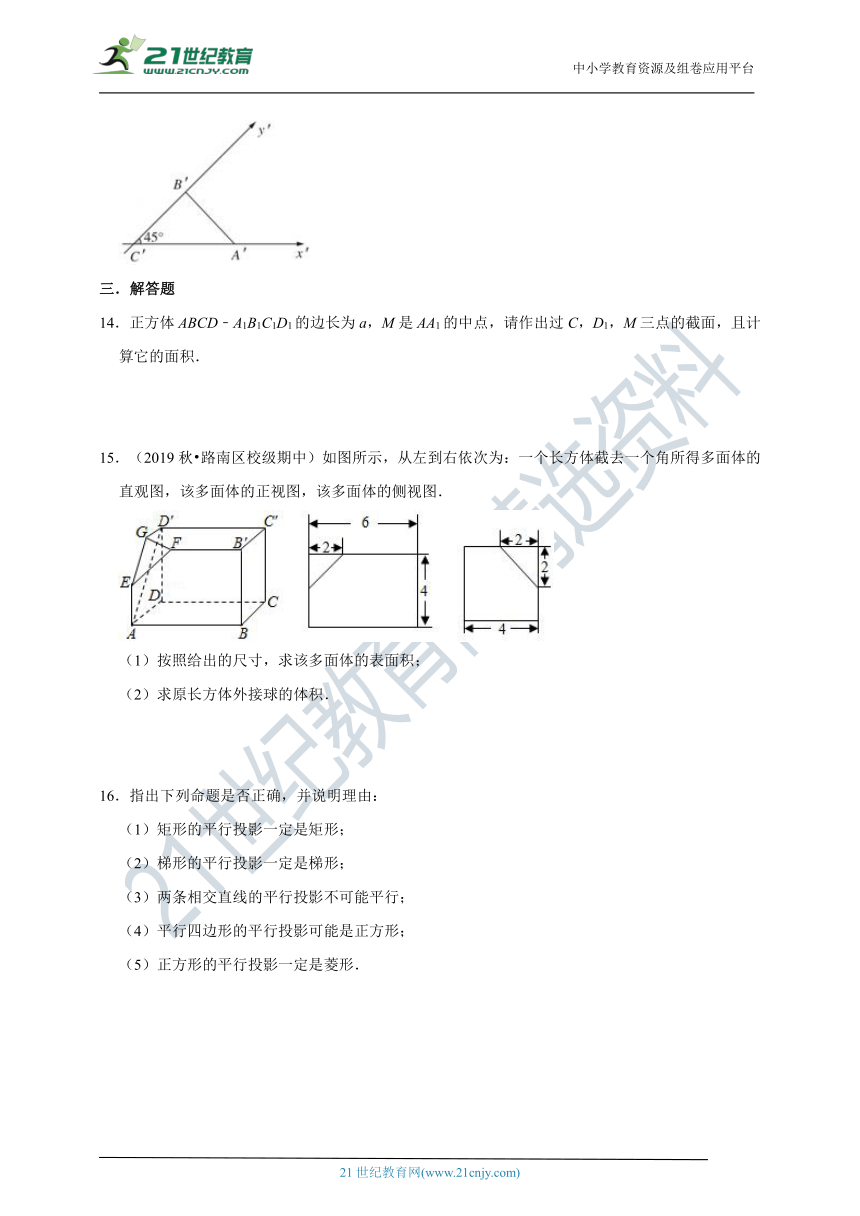
8.(2020春?威宁县期末)已知一个半圆柱的高为4,其俯视图如图所示,侧视图的面积为8,则该半圆柱的底面半圆的半径为
.
9.(2012?江阴市模拟)已知正四面体棱长为1,则其在平面α内的投影面积最大值是
.
10.(2019秋?上虞区期末)某几何体的正视图和侧视图如图1所示,俯视图的直观图如图2所示,则该几何体的表面积为
,体积为
.
11.(2020春?徐州期中)正方形OABC的边长是1cm,在直观图(如图所示)中,四边形O′A′B′C′的面积为
cm2.
12.(2018?东城区二模)如图,已知正方体ABCD﹣A'B'C'D'的边长为1,若过直线BD'的平面与该正方体的面相交,交线围成一个菱形,则该菱形的面积为
.
13.(2020春?石家庄期末)水平放置的△ABC的直观图如图所示,已知A'C′=4,B'C,则原图中AB边上中线的实际长度为
.
三.解答题
14.正方体ABCD﹣A1B1C1D1的边长为a,M是AA1的中点,请作出过C,D1,M三点的截面,且计算它的面积.
15.(2019秋?路南区校级期中)如图所示,从左到右依次为:一个长方体截去一个角所得多面体的直观图,该多面体的正视图,该多面体的侧视图.
(1)按照给出的尺寸,求该多面体的表面积;
(2)求原长方体外接球的体积.
16.指出下列命题是否正确,并说明理由:
(1)矩形的平行投影一定是矩形;
(2)梯形的平行投影一定是梯形;
(3)两条相交直线的平行投影不可能平行;
(4)平行四边形的平行投影可能是正方形;
(5)正方形的平行投影一定是菱形.
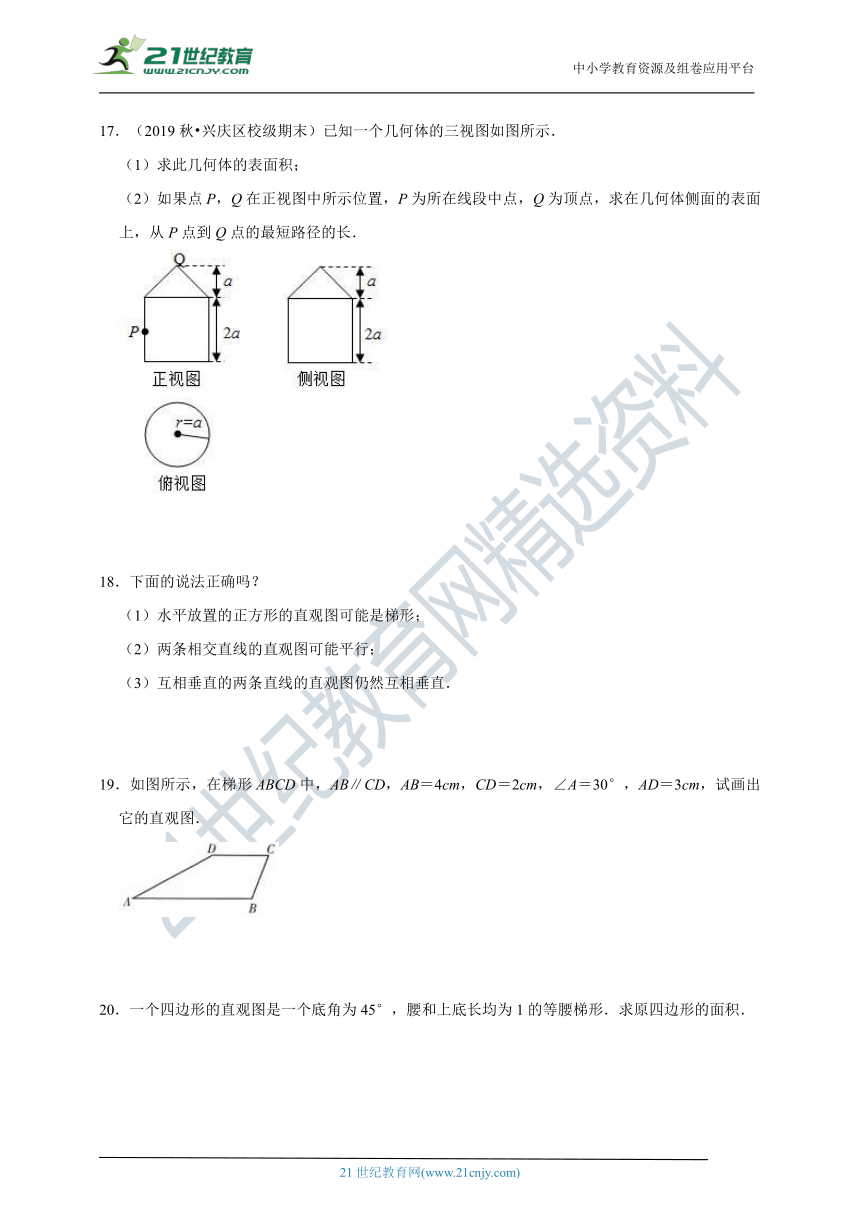
17.(2019秋?兴庆区校级期末)已知一个几何体的三视图如图所示.
(1)求此几何体的表面积;
(2)如果点P,Q在正视图中所示位置,P为所在线段中点,Q为顶点,求在几何体侧面的表面上,从P点到Q点的最短路径的长.
18.下面的说法正确吗?
(1)水平放置的正方形的直观图可能是梯形;
(2)两条相交直线的直观图可能平行;
(3)互相垂直的两条直线的直观图仍然互相垂直.
19.如图所示,在梯形ABCD中,AB∥CD,AB=4cm,CD=2cm,∠A=30°,AD=3cm,试画出它的直观图.
20.一个四边形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形.求原四边形的面积.
21.用斜二测画法画出下列正方形和等边三角形水平放置的直观图.
参考答案与试题解析
一.选择题
1.【解答】解:当截面平行于正方体的一个侧面时得C,
当截面过正方体的体对角面时得B,
当截面不平行于任何侧面和对角面时得A,
但无论如何都不能截出D,
故选:D.
2.【解答】解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
其中PA⊥平面ABCD,∴PA=3,AB=CD=4,AD=BC=5,
∴PB5,
PC5,
PD.
该几何体最长棱的棱长为:5.
故选:D.
3.【解答】解:由已知中的空间几何体的正视图和俯视图可得:
该几何体是一个底面半径为1,高为1的圆柱挖去一个同底等高的圆锥所得的组合体,
故其侧视图为:
故选:B.
4.【解答】解:从上下方向上看,△PAC的投影为①图所示的情况;
从左右方向上看,△PAC的投影为④图所示的情况;
从前后方向上看,△PAC的投影为④图所示的情况;
故选:A.
5.【解答】解:因为,
且若△A′B′C′的面积为2,
那么△ABC的面积为
.
故选:A.
6.【解答】解:由斜二测画法规则知:三角形的直观图仍然是三角形,所以①正确;
根据平行性不变知,平行四边形的直观图还是平行四边形,所以②正确;
根据x′O′y′两轴的夹角为45°或135°知,菱形的直观图不再是菱形,所以③错误;
根据平行于x轴的长度不变,平行于y轴的长度减半知,正方形的直观图不再是正方形,所以④错误.
故选:B.
7.【解答】解:由题意,直观图的三角形面积为a2,
因为直观图和原图面积之间的关系为2,
所以原三角形的面积是2a2a2.
故选:D.
二.填空题
8.【解答】解:半圆柱的立体图如图所示,其侧视图是矩形ABCD,
所以AB?AD=8,即4×AD=8,所以AD=2,
所以半圆柱的底面半圆的半径为2.
故答案为:2.
9.【解答】解:由题意当线段AB相对的侧棱与投影面平行时投影最大,此时投影是关于线段AB对称的两个等腰三角形,
由于正四面体的棱长都是1,故投影面积为1×1
故答案为:
10.【解答】解:由图2可得底面为的平行四边形,且底为6,高为4,则可得另一条边长为3,图1可知高为4的直四棱柱,
所以S表=2底+S侧=22(6+3)?4=48+72,
V=Sh=696,
故答案分别为:48+72,96.
11.【解答】解:因为正方形OABC的边长是1cm,
所以原图形的面积为:1×1=1;
故四边形O′A′B′C′的面积为:S原图;
故答案为:.
12.【解答】解:取AA′的中点E,CC′的中点为F,连接BED′F,可得四边形是菱形,两条对角线的长为:,;则菱形的面积为:S.
故答案为:.
13.【解答】解:由直观图得出原平面图形△ABC,如图所示;
则直观图中A′C′=4,B′C′,
所以△ABC是直角三角形,且AC=4,BC=3,所以AB=5,
所以AB边上的中线长度为.
故答案为:.
三.解答题
14.【解答】解:如图,由面面平行的性质知截面与平面AB1的交线MN是△AA1B的中位线,所以截面是梯形CD1MN,
由题意,MNa,D1Ca,MD1a
∴梯形的高为a,
∴梯形CD1MN的面积为.
15.【解答】解:(1)由题意可知几何体的表面积为:6×(4+4+4+4)+2×4×4﹣3122+2.
(2)原长方体外接球的半径为:,
原长方体外接球的体积:.
16.【解答】解:(1)不正确,因为矩形的平行投影可能是一条线段;
(2)不正确,因为梯形的平行投影可能是一条线段;
(3)正确,若两条直线的平行投影平行,则此两条直线必为平行直线或异面直线,
两条相交直线的平行投影必有公共点,因此不可能平行;
(4)正确,平行四边形的平行投影可能是正方形;
(5)不正确,正方形的平行投影可能是平行四边形,或为一条线段.
17.【解答】解:(1)根据几何体的三视图,转换为几何体,是由一个圆锥和一个圆柱组成.
该几何体的表面积是由圆锥的侧面积和圆柱的侧面积及圆柱的底面积组成.
所以.
.
.
.
(2)沿点P与点Q所在的母线剪开圆柱的侧面,
如图所示:
所以PQ,即最短路径.
18.【解答】解:根据直观图的做法,在做直观图时,原来与横轴平行的与X′平行,且长度不变,
原来与y轴平行的与y′平行,长度变为原来的一半,
且新的坐标轴之间的夹角是45度,
∴原来垂直的画出直观图不一定垂直,
原来是对边平行的仍然平行,
故(1)(2)(3)均是错的.
19.【解答】解:①在已知梯形ABCD中,过点D作DO⊥AB于点O,
∵AD=3cm,∠A=30°,∴ODcm,OAcm,OB=4cm,
以O为原点,AB、OD所在的直线分别为x、y轴,画对应的x'、y'轴,使∠x'O'y'=45°;
②在x'轴上取O'A'cm,O'B'=4cm,在y'轴上取O'D'ODcm,过点D'作D'C'∥x'轴,且D'C'=CD=2cm;
③连结A'D'、B'C',所得四边形A'B'C'D'即为梯形ABCD的直观图.
20.【解答】解:∵四边形的斜二侧直观图是一个底角为45°,腰和上底的长均为1的等腰梯形,
∴可设原四边形为直角梯形ABCD,
且CD=C'D'=1,AB=O'B11,高AD=20'D'=2,
∴直角梯形ABCD的面积为:(11)=2,
即原四边形的面积为:2.
21.【解答】解:在已知图形中取互相垂直的x轴和y轴,两轴相交于O点,画直观图时,把它画成对应的x′轴、y′轴,使∠x′Oy′=45°(或135°),它确定的平面表示水平平面.
已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′或y′轴的线段,如图AB
的线段,DC线段的长度不变,
已知图形中平行于x轴的线段,在直观图中保持原长度不变;
平行于y轴的线段,长度为原来的一半.在第一个图形中的AD,BC,
平面图形的直观图如图:.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题基础练
第一章《空间几何体》
1.2
空间几何体的三视图和直观图
一.选择题
1.(2020春?雨花区校级月考)一个正方体内接于一个球,过球心作一个截面,则截面不可能的图形为( )
A.
B.
C.
D.
2.(2020秋?龙凤区校级期末)《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(网格纸上小正方形的边长为1),则该“阳马”最长的棱长为( )
A.5
B.
C.
D.
3.(2020秋?榆林期末)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A.
B.
C.
D.
4.(2020?芜湖模拟)如图,在正方体ABCD﹣A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是( )
A.①④
B.②③
C.②④
D.①②
5.(2020秋?秦都区校级月考)已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′C′,那么原△ABC的面积是( )
A.
B.2
C.
D.
6.(2020秋?镜湖区校级期中)下列关于斜二测画法所得直观图的说法中正确的有( )
①三角形的直观图是三角形.
②平行四边形的直观图是平行四边形.
③菱形的直观图是菱形.④正方形的直观图是正方形.
A.①
B.①②
C.③④
D.①②③④
7.(2020秋?瑶海区校级期中)一个平面图形的斜二测画法的直观图是一个直角边为a的等腰直角三角形,则原图形的面积为( )
A.
B.
C.
D.
二.填空题
8.(2020春?威宁县期末)已知一个半圆柱的高为4,其俯视图如图所示,侧视图的面积为8,则该半圆柱的底面半圆的半径为
.
9.(2012?江阴市模拟)已知正四面体棱长为1,则其在平面α内的投影面积最大值是
.
10.(2019秋?上虞区期末)某几何体的正视图和侧视图如图1所示,俯视图的直观图如图2所示,则该几何体的表面积为
,体积为
.
11.(2020春?徐州期中)正方形OABC的边长是1cm,在直观图(如图所示)中,四边形O′A′B′C′的面积为
cm2.
12.(2018?东城区二模)如图,已知正方体ABCD﹣A'B'C'D'的边长为1,若过直线BD'的平面与该正方体的面相交,交线围成一个菱形,则该菱形的面积为
.
13.(2020春?石家庄期末)水平放置的△ABC的直观图如图所示,已知A'C′=4,B'C,则原图中AB边上中线的实际长度为
.
三.解答题
14.正方体ABCD﹣A1B1C1D1的边长为a,M是AA1的中点,请作出过C,D1,M三点的截面,且计算它的面积.
15.(2019秋?路南区校级期中)如图所示,从左到右依次为:一个长方体截去一个角所得多面体的直观图,该多面体的正视图,该多面体的侧视图.
(1)按照给出的尺寸,求该多面体的表面积;
(2)求原长方体外接球的体积.
16.指出下列命题是否正确,并说明理由:
(1)矩形的平行投影一定是矩形;
(2)梯形的平行投影一定是梯形;
(3)两条相交直线的平行投影不可能平行;
(4)平行四边形的平行投影可能是正方形;
(5)正方形的平行投影一定是菱形.
17.(2019秋?兴庆区校级期末)已知一个几何体的三视图如图所示.
(1)求此几何体的表面积;
(2)如果点P,Q在正视图中所示位置,P为所在线段中点,Q为顶点,求在几何体侧面的表面上,从P点到Q点的最短路径的长.
18.下面的说法正确吗?
(1)水平放置的正方形的直观图可能是梯形;
(2)两条相交直线的直观图可能平行;
(3)互相垂直的两条直线的直观图仍然互相垂直.
19.如图所示,在梯形ABCD中,AB∥CD,AB=4cm,CD=2cm,∠A=30°,AD=3cm,试画出它的直观图.
20.一个四边形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形.求原四边形的面积.
21.用斜二测画法画出下列正方形和等边三角形水平放置的直观图.
参考答案与试题解析
一.选择题
1.【解答】解:当截面平行于正方体的一个侧面时得C,
当截面过正方体的体对角面时得B,
当截面不平行于任何侧面和对角面时得A,
但无论如何都不能截出D,
故选:D.
2.【解答】解:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
其中PA⊥平面ABCD,∴PA=3,AB=CD=4,AD=BC=5,
∴PB5,
PC5,
PD.
该几何体最长棱的棱长为:5.
故选:D.
3.【解答】解:由已知中的空间几何体的正视图和俯视图可得:
该几何体是一个底面半径为1,高为1的圆柱挖去一个同底等高的圆锥所得的组合体,
故其侧视图为:
故选:B.
4.【解答】解:从上下方向上看,△PAC的投影为①图所示的情况;
从左右方向上看,△PAC的投影为④图所示的情况;
从前后方向上看,△PAC的投影为④图所示的情况;
故选:A.
5.【解答】解:因为,
且若△A′B′C′的面积为2,
那么△ABC的面积为
.
故选:A.
6.【解答】解:由斜二测画法规则知:三角形的直观图仍然是三角形,所以①正确;
根据平行性不变知,平行四边形的直观图还是平行四边形,所以②正确;
根据x′O′y′两轴的夹角为45°或135°知,菱形的直观图不再是菱形,所以③错误;
根据平行于x轴的长度不变,平行于y轴的长度减半知,正方形的直观图不再是正方形,所以④错误.
故选:B.
7.【解答】解:由题意,直观图的三角形面积为a2,
因为直观图和原图面积之间的关系为2,
所以原三角形的面积是2a2a2.
故选:D.
二.填空题
8.【解答】解:半圆柱的立体图如图所示,其侧视图是矩形ABCD,
所以AB?AD=8,即4×AD=8,所以AD=2,
所以半圆柱的底面半圆的半径为2.
故答案为:2.
9.【解答】解:由题意当线段AB相对的侧棱与投影面平行时投影最大,此时投影是关于线段AB对称的两个等腰三角形,
由于正四面体的棱长都是1,故投影面积为1×1
故答案为:
10.【解答】解:由图2可得底面为的平行四边形,且底为6,高为4,则可得另一条边长为3,图1可知高为4的直四棱柱,
所以S表=2底+S侧=22(6+3)?4=48+72,
V=Sh=696,
故答案分别为:48+72,96.
11.【解答】解:因为正方形OABC的边长是1cm,
所以原图形的面积为:1×1=1;
故四边形O′A′B′C′的面积为:S原图;
故答案为:.
12.【解答】解:取AA′的中点E,CC′的中点为F,连接BED′F,可得四边形是菱形,两条对角线的长为:,;则菱形的面积为:S.
故答案为:.
13.【解答】解:由直观图得出原平面图形△ABC,如图所示;
则直观图中A′C′=4,B′C′,
所以△ABC是直角三角形,且AC=4,BC=3,所以AB=5,
所以AB边上的中线长度为.
故答案为:.
三.解答题
14.【解答】解:如图,由面面平行的性质知截面与平面AB1的交线MN是△AA1B的中位线,所以截面是梯形CD1MN,
由题意,MNa,D1Ca,MD1a
∴梯形的高为a,
∴梯形CD1MN的面积为.
15.【解答】解:(1)由题意可知几何体的表面积为:6×(4+4+4+4)+2×4×4﹣3122+2.
(2)原长方体外接球的半径为:,
原长方体外接球的体积:.
16.【解答】解:(1)不正确,因为矩形的平行投影可能是一条线段;
(2)不正确,因为梯形的平行投影可能是一条线段;
(3)正确,若两条直线的平行投影平行,则此两条直线必为平行直线或异面直线,
两条相交直线的平行投影必有公共点,因此不可能平行;
(4)正确,平行四边形的平行投影可能是正方形;
(5)不正确,正方形的平行投影可能是平行四边形,或为一条线段.
17.【解答】解:(1)根据几何体的三视图,转换为几何体,是由一个圆锥和一个圆柱组成.
该几何体的表面积是由圆锥的侧面积和圆柱的侧面积及圆柱的底面积组成.
所以.
.
.
.
(2)沿点P与点Q所在的母线剪开圆柱的侧面,
如图所示:
所以PQ,即最短路径.
18.【解答】解:根据直观图的做法,在做直观图时,原来与横轴平行的与X′平行,且长度不变,
原来与y轴平行的与y′平行,长度变为原来的一半,
且新的坐标轴之间的夹角是45度,
∴原来垂直的画出直观图不一定垂直,
原来是对边平行的仍然平行,
故(1)(2)(3)均是错的.
19.【解答】解:①在已知梯形ABCD中,过点D作DO⊥AB于点O,
∵AD=3cm,∠A=30°,∴ODcm,OAcm,OB=4cm,
以O为原点,AB、OD所在的直线分别为x、y轴,画对应的x'、y'轴,使∠x'O'y'=45°;
②在x'轴上取O'A'cm,O'B'=4cm,在y'轴上取O'D'ODcm,过点D'作D'C'∥x'轴,且D'C'=CD=2cm;
③连结A'D'、B'C',所得四边形A'B'C'D'即为梯形ABCD的直观图.
20.【解答】解:∵四边形的斜二侧直观图是一个底角为45°,腰和上底的长均为1的等腰梯形,
∴可设原四边形为直角梯形ABCD,
且CD=C'D'=1,AB=O'B11,高AD=20'D'=2,
∴直角梯形ABCD的面积为:(11)=2,
即原四边形的面积为:2.
21.【解答】解:在已知图形中取互相垂直的x轴和y轴,两轴相交于O点,画直观图时,把它画成对应的x′轴、y′轴,使∠x′Oy′=45°(或135°),它确定的平面表示水平平面.
已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x′或y′轴的线段,如图AB
的线段,DC线段的长度不变,
已知图形中平行于x轴的线段,在直观图中保持原长度不变;
平行于y轴的线段,长度为原来的一半.在第一个图形中的AD,BC,
平面图形的直观图如图:.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
