【同步必刷题】1.2 空间几何体的三视图和直观图 提高练(含解析)
文档属性
| 名称 | 【同步必刷题】1.2 空间几何体的三视图和直观图 提高练(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-25 14:41:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2020-2021学年人教A版必修二同步必刷题提高练
第一章《空间几何体》
1.2
空间几何体的三视图和直观图
一.选择题
1.(2021?五模拟)在边长为1的正方形网格中,某几何体的三视图如图所示,则该几何体的表面积为( )
A.2(1)
B.2(2)
C.2(1+2)
D.2(1+22)
2.(2021?十模拟)如图是某四棱锥的三视图,则该四棱锥的体积为( )
A.12
B.14
C.16
D.18
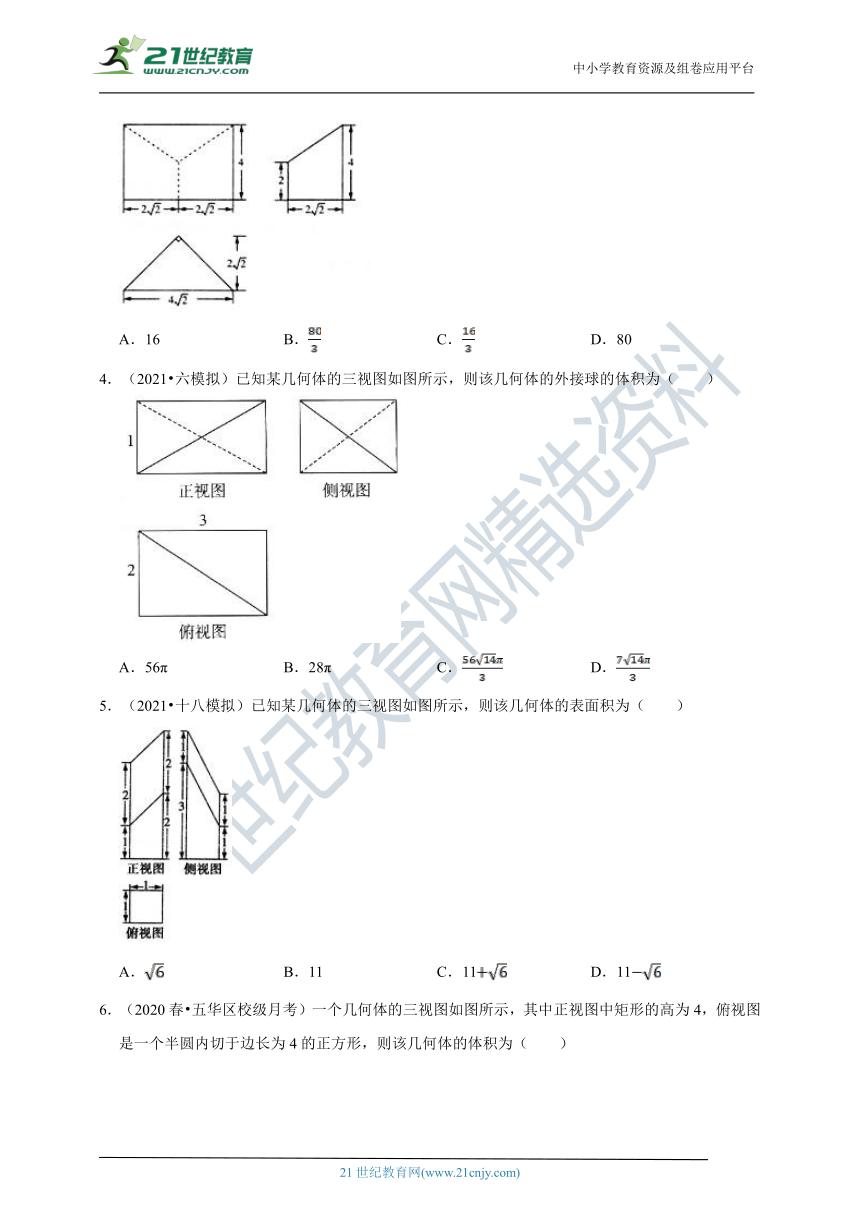
3.(2021?十三模拟)已知某空间几何体的三视图如图所示,则该几何体的体积是( )
A.16
B.
C.
D.80
4.(2021?六模拟)已知某几何体的三视图如图所示,则该几何体的外接球的体积为( )
A.56π
B.28π
C.
D.
5.(2021?十八模拟)已知某几何体的三视图如图所示,则该几何体的表面积为( )
A.
B.11
C.11
D.11
6.(2020春?五华区校级月考)一个几何体的三视图如图所示,其中正视图中矩形的高为4,俯视图是一个半圆内切于边长为4的正方形,则该几何体的体积为( )
A.
B.
C.
D.
7.(2020?运城模拟)如图是某几何体的三视图,则该几何体的表面积为( )
A.
B.
C.
D.
8.(2020?衡阳三模)如图,直三棱柱ABC﹣A1B1C1的正视图和俯视图分别为矩形和正三角形,该三棱柱各顶点都在球O的球面上,过AB中点E作球O的截面,则截面面积的最小值为( )
A.3π
B.6π
C.9π
D.12π
二.填空题
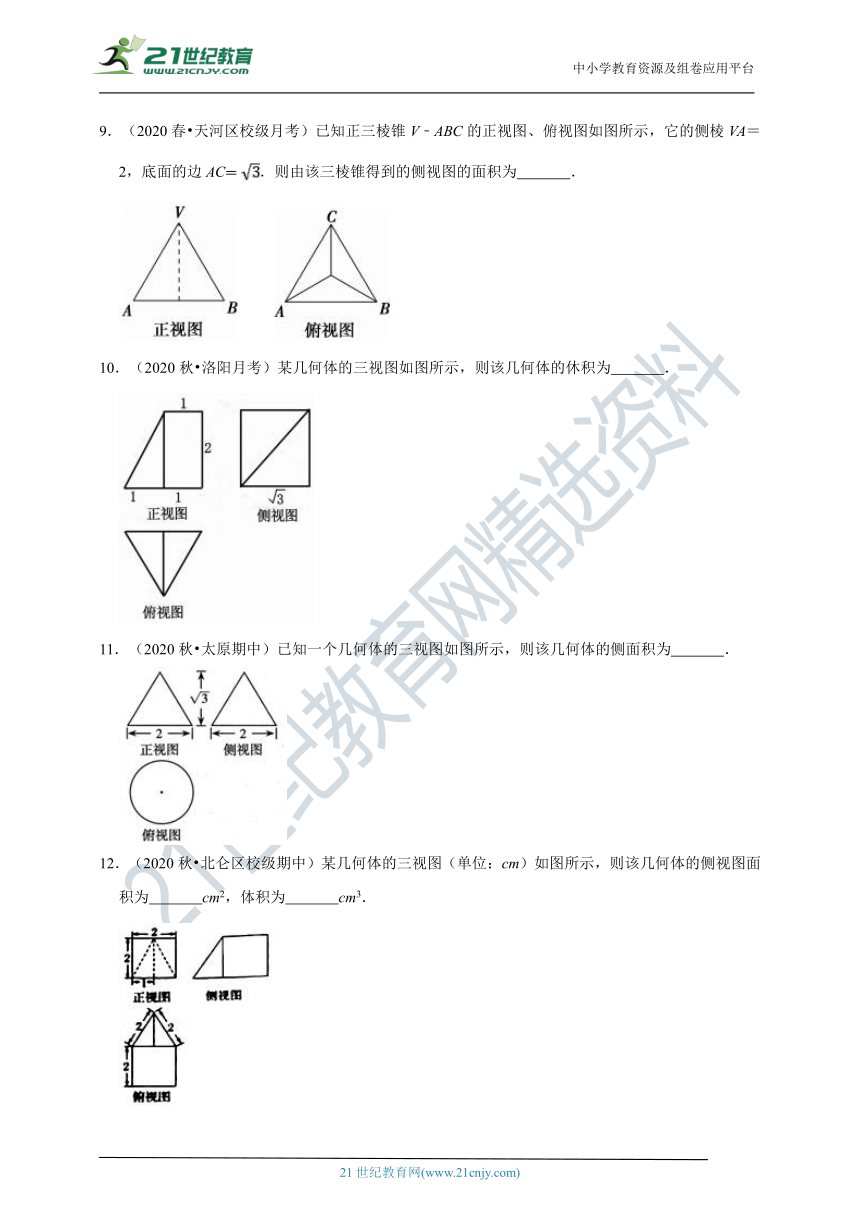
9.(2020春?天河区校级月考)已知正三棱锥V﹣ABC的正视图、俯视图如图所示,它的侧棱VA=2,底面的边AC.则由该三棱锥得到的侧视图的面积为
.
10.(2020秋?洛阳月考)某几何体的三视图如图所示,则该几何体的休积为
.
11.(2020秋?太原期中)已知一个几何体的三视图如图所示,则该几何体的侧面积为
.
12.(2020秋?北仑区校级期中)某几何体的三视图(单位:cm)如图所示,则该几何体的侧视图面积为
cm2,体积为
cm3.
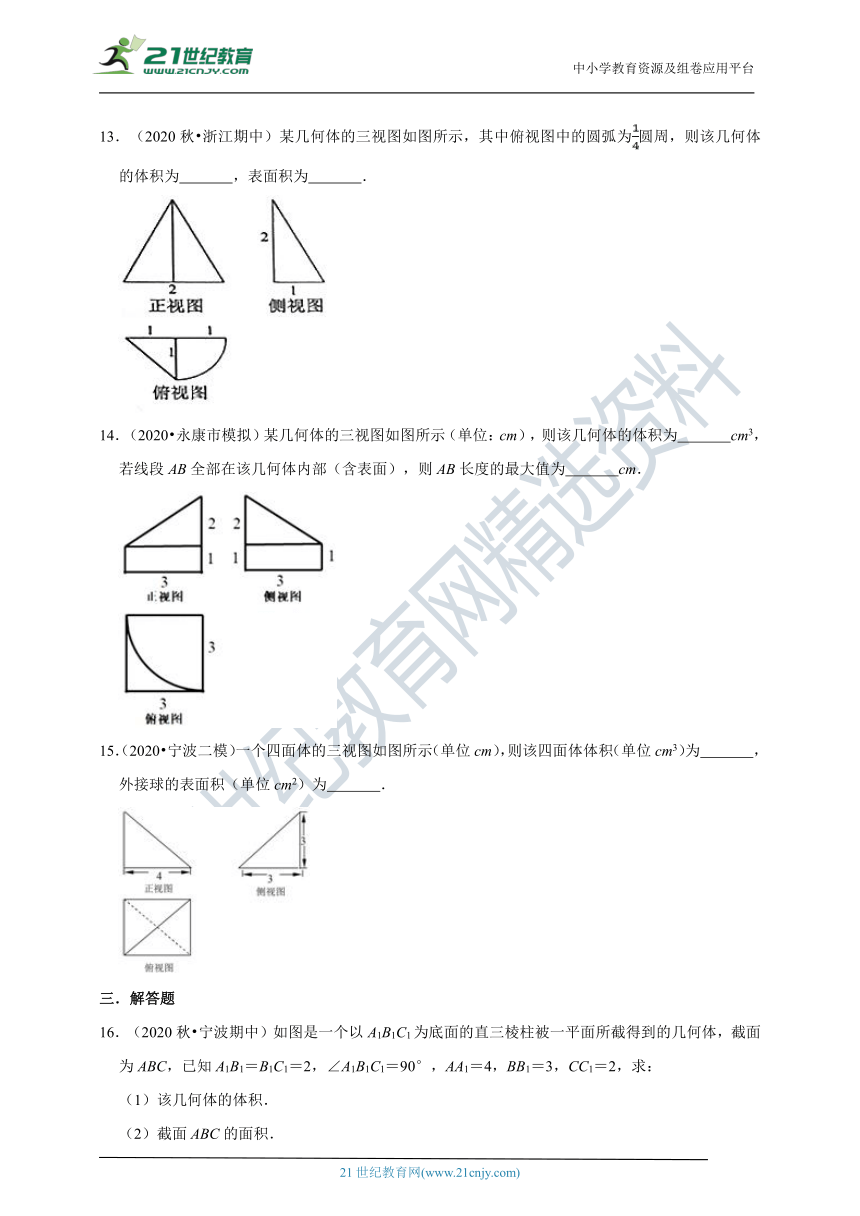
13.(2020秋?浙江期中)某几何体的三视图如图所示,其中俯视图中的圆弧为圆周,则该几何体的体积为
,表面积为
.
14.(2020?永康市模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积为
cm3,若线段AB全部在该几何体内部(含表面),则AB长度的最大值为
cm.
15.(2020?宁波二模)一个四面体的三视图如图所示(单位cm),则该四面体体积(单位cm3)为
,外接球的表面积(单位cm2)为
.
三.解答题
16.(2020秋?宁波期中)如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
(1)该几何体的体积.
(2)截面ABC的面积.
17.(2019秋?芜湖期末)某个几何体的三视图如图所示(单位:m):
(1)求该几何体的表面积;
(2)求该几何体的体积.
18.(2019春?临夏市校级期中)某几何体的三视图如图所示,求该几何体的体积.
19.(2020秋?瑶海区校级月考)如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
(1)说明该几何体是由哪些简单的几何体组成;
(2)求该几何体的表面积与体积.
20.(2020秋?包河区校级月考)一个几何体的三视图如图所示,求该几何体的表面积和体积.
21.(2020春?昌吉市期末)如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
22.(2020春?梅河口市校级月考)如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.
参考答案与试题解析
一.选择题
1.【解答】解:根据几何体的三视图,转换为直观图为:
该几何体为三棱锥体,
如图所示:
所以
S△OBC+S△OBA+S△ABC+S△AOC.
故选:C.
2.【解答】解:根据几何体的三视图转换为几何体的直观图为:该几何体为四棱锥体;
如图所示:
故直线PA⊥平面ABCD,
所以PA=AB=BC=2AD=4,
则,
故选:C.
3.【解答】解:几何体的直观图如图:是一个三棱柱截去一个三棱锥的几何体,
三棱柱的底面是腰长为4的等腰直角三角形,棱柱的高为4,截去棱锥的高为2,
所求几何体的体积为:.
故选:B.
4.【解答】解:由题意,几何体的直观图如图,是多面体ABCDC′A′,
构造长方体ABCD﹣A′B′C′D′,其中BC=3,AB=2,AA′=1,
长方体的外接球就是多面体的外接球,
设球的半径为R,所以2R,
所以球的体积为:
V.
故选:D.
5.【解答】解答:解:由三视图知:几何体的直观图如图:
其中HEFG是平行四边形,连接HF,可得HG,GF,HF,所以HF2+HG2=GF2,FH⊥HG,所以几何体的表面积为:1×
111.
故选:C.
6.【解答】解:由三视图还原原几何体如图,
可知该几何体是组合体,上半部分是半径为2的球的四分之一,下半部分是棱长为4的正方体,
则该几何体的体积为,
故选:A.
7.【解答】解:由三视图还原原几何体如图,
该几何体为三棱锥P﹣ABCD挖去半个圆锥,
四棱锥的底面是边长为2的正方形,圆锥的底面半径为1,高为2.
则该几何体的表面积为
.
故选:D.
8.【解答】解:由正视图及俯视图可知ABC﹣A1B1C1为正三棱柱,底面ABC边长为6,如图,O2,O1分别为三棱柱上下底面的中心,
则ABC﹣A1B1C1的外接球球心O为O1O2的中点,其半径,
要使AB中点E作球O的截面最小,只须使球心O到截面的距离d最大即可.
此时过E的截面垂直于OE,
截面半径,
所以截面面积,
故选:C.
二.填空题
9.【解答】解:正三棱锥V﹣ABC中,侧棱长VA=2,底面三角形的边长AC,
可得底面三角形的高为:,
V到底面的距离:;
该三棱锥的侧视图的面积:.
故答案为:.
10.【解答】解:根据几何体的三视图转换为直观图为:
该几何体为由一个三棱柱和一个四棱锥构成的组合体.
如图所示:
故.
故答案为:.
11.【解答】解:由题意可知几何体是圆锥,底面半径为1,高为,母线为:2.
所以几何体的侧面积为:2π,
故答案为:2π.
12.【解答】解:由题意可知几何体是一个棱长为2正方体与一个底面是正三角形,一个侧面与在正方体的侧面的三棱锥组成,几何体的直观图如图:
所以侧视图的面积为:2×24.
几何体的体积为:2×2×28.
故答案为:4;8.
13.【解答】解:根据几何体的三视图转换为直观图为:由一个三棱锥体和一个圆锥组成的几何体.
如图所示:V.
所以表面积为:S底+S侧.
故答案为:;.
14.【解答】解:由三视图还原原几何体如图,
该几何体为组合体,下半部分为长方体,底面是边长为2的正方体,高为1,
上半部分为四分之一圆锥,圆锥的底面半径为3,高为2.
则该几何体的体积Vcm3,
由已知求得圆锥的母线长为.
连接图中PM,求得PM,设PM交长方体上底面于N,
由相似三角形对应边成比例可得PN,
则A,B分别与P,M重合时,满足AB全部在该几何体内部,且AB长度最大为cm.
故答案为:9;.
15.【解答】解:由三视图还原原几何体如图,
该几何体为三棱锥P﹣ABC,底面三角形ABC为直角三角形,
AB⊥BC,AB=3,BC=4,三棱锥的高为PD=3.
则其体积V;
把该三棱锥补形为长方体,则其外接球的半径R.
∴其外接球的表面积S.
故答案为:6;34π.
三.解答题
16.【解答】解:(1)以同样大的几何体,进行补形,可得一直三棱柱,
其底面为△A1B1C1,高为3×2=6,
∴所求几何体的体积为
Vh2×2×6=6;
(2)△ABC中,AB,
BC,
AC2,
∴△ABC为等腰三角形,底边AC的高为:
h;
∴截面ABC的面积为
S△ABC2.
17.【解答】解:由三视图可知,该几何体是由半球和正四棱柱组成,棱柱是正方体棱长为:2,球的半径为1,
(1)该几何体的表面积=正方体的表面积+半球面面积﹣球的底面积.
∴S=6×2×2+2π×12﹣π×12=24+π(m2).
(2)该几何体的体积为正方体的体积+半球的体积,
V=2×2×2π×13=8π(m3)
18.【解答】解:根据几何体的三视图转换为几何体为:该几何体为四棱柱.
如图所示:
所以:V,
所以该几何体的体积为3.
19.【解答】解:(1)由三视图知,该三视图对应的几何体为一个底面直径为2,母线长为2的圆锥与一个长宽都为2高为1的长方体组成的组合体.(2分)
(2)此几何体的表面积:S=2π+2×4﹣π+4×2=π+16(6分)
此几何体的体积:Vπ+4(10分)
20.【解答】解:由已知中的三视图,可得:该几何体是一个长方体挖去一个圆柱所得的组合体,
长方体的长宽高分别为4,3,1,
故长方体的体积为:12,
圆柱的底面半径为1,高为1,
故圆柱的体积为:π,
故组合体的体积为:12﹣π,
长方体的表面积为:2(1×3+1×4+3×4)=38,
圆柱的底面积为π,
侧面积为:2π,
故几何体的表面积为:38﹣2π+2π=38.
21.【解答】解:由三视图可知该几何体是由上下两部分组成:上面是直径为2的球;下面是一个长方体,其长宽高分别为2,2,3,且球切于长方体上底面的圆心.
∴S表面积=4π×12+2×(2×2+2×3+2×3)=4π+32.
V体积π×13+2×2×312.
22.【解答】解:由三视图知几何体是一个组合体,下半部是长方体,上半部是半圆柱,
其轴截面的大小与长方体的上底面大小一致.
长方体的棱长分别是4,6,8
圆柱的高是8,底面圆的半径是2
∴表面积为S=32+96+48+4π+16π=176+20π,
体积为V=192+16π,
即几何体的表面积为176+20πcm2,体积为192+16πcm3
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年人教A版必修二同步必刷题提高练
第一章《空间几何体》
1.2
空间几何体的三视图和直观图
一.选择题
1.(2021?五模拟)在边长为1的正方形网格中,某几何体的三视图如图所示,则该几何体的表面积为( )
A.2(1)
B.2(2)
C.2(1+2)
D.2(1+22)
2.(2021?十模拟)如图是某四棱锥的三视图,则该四棱锥的体积为( )
A.12
B.14
C.16
D.18
3.(2021?十三模拟)已知某空间几何体的三视图如图所示,则该几何体的体积是( )
A.16
B.
C.
D.80
4.(2021?六模拟)已知某几何体的三视图如图所示,则该几何体的外接球的体积为( )
A.56π
B.28π
C.
D.
5.(2021?十八模拟)已知某几何体的三视图如图所示,则该几何体的表面积为( )
A.
B.11
C.11
D.11
6.(2020春?五华区校级月考)一个几何体的三视图如图所示,其中正视图中矩形的高为4,俯视图是一个半圆内切于边长为4的正方形,则该几何体的体积为( )
A.
B.
C.
D.
7.(2020?运城模拟)如图是某几何体的三视图,则该几何体的表面积为( )
A.
B.
C.
D.
8.(2020?衡阳三模)如图,直三棱柱ABC﹣A1B1C1的正视图和俯视图分别为矩形和正三角形,该三棱柱各顶点都在球O的球面上,过AB中点E作球O的截面,则截面面积的最小值为( )
A.3π
B.6π
C.9π
D.12π
二.填空题
9.(2020春?天河区校级月考)已知正三棱锥V﹣ABC的正视图、俯视图如图所示,它的侧棱VA=2,底面的边AC.则由该三棱锥得到的侧视图的面积为
.
10.(2020秋?洛阳月考)某几何体的三视图如图所示,则该几何体的休积为
.
11.(2020秋?太原期中)已知一个几何体的三视图如图所示,则该几何体的侧面积为
.
12.(2020秋?北仑区校级期中)某几何体的三视图(单位:cm)如图所示,则该几何体的侧视图面积为
cm2,体积为
cm3.
13.(2020秋?浙江期中)某几何体的三视图如图所示,其中俯视图中的圆弧为圆周,则该几何体的体积为
,表面积为
.
14.(2020?永康市模拟)某几何体的三视图如图所示(单位:cm),则该几何体的体积为
cm3,若线段AB全部在该几何体内部(含表面),则AB长度的最大值为
cm.
15.(2020?宁波二模)一个四面体的三视图如图所示(单位cm),则该四面体体积(单位cm3)为
,外接球的表面积(单位cm2)为
.
三.解答题
16.(2020秋?宁波期中)如图是一个以A1B1C1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
(1)该几何体的体积.
(2)截面ABC的面积.
17.(2019秋?芜湖期末)某个几何体的三视图如图所示(单位:m):
(1)求该几何体的表面积;
(2)求该几何体的体积.
18.(2019春?临夏市校级期中)某几何体的三视图如图所示,求该几何体的体积.
19.(2020秋?瑶海区校级月考)如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
(1)说明该几何体是由哪些简单的几何体组成;
(2)求该几何体的表面积与体积.
20.(2020秋?包河区校级月考)一个几何体的三视图如图所示,求该几何体的表面积和体积.
21.(2020春?昌吉市期末)如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
22.(2020春?梅河口市校级月考)如图是某几何体的三视图,请你指出这个几何体的结构特征,并求出它的表面积与体积.
参考答案与试题解析
一.选择题
1.【解答】解:根据几何体的三视图,转换为直观图为:
该几何体为三棱锥体,
如图所示:
所以
S△OBC+S△OBA+S△ABC+S△AOC.
故选:C.
2.【解答】解:根据几何体的三视图转换为几何体的直观图为:该几何体为四棱锥体;
如图所示:
故直线PA⊥平面ABCD,
所以PA=AB=BC=2AD=4,
则,
故选:C.
3.【解答】解:几何体的直观图如图:是一个三棱柱截去一个三棱锥的几何体,
三棱柱的底面是腰长为4的等腰直角三角形,棱柱的高为4,截去棱锥的高为2,
所求几何体的体积为:.
故选:B.
4.【解答】解:由题意,几何体的直观图如图,是多面体ABCDC′A′,
构造长方体ABCD﹣A′B′C′D′,其中BC=3,AB=2,AA′=1,
长方体的外接球就是多面体的外接球,
设球的半径为R,所以2R,
所以球的体积为:
V.
故选:D.
5.【解答】解答:解:由三视图知:几何体的直观图如图:
其中HEFG是平行四边形,连接HF,可得HG,GF,HF,所以HF2+HG2=GF2,FH⊥HG,所以几何体的表面积为:1×
111.
故选:C.
6.【解答】解:由三视图还原原几何体如图,
可知该几何体是组合体,上半部分是半径为2的球的四分之一,下半部分是棱长为4的正方体,
则该几何体的体积为,
故选:A.
7.【解答】解:由三视图还原原几何体如图,
该几何体为三棱锥P﹣ABCD挖去半个圆锥,
四棱锥的底面是边长为2的正方形,圆锥的底面半径为1,高为2.
则该几何体的表面积为
.
故选:D.
8.【解答】解:由正视图及俯视图可知ABC﹣A1B1C1为正三棱柱,底面ABC边长为6,如图,O2,O1分别为三棱柱上下底面的中心,
则ABC﹣A1B1C1的外接球球心O为O1O2的中点,其半径,
要使AB中点E作球O的截面最小,只须使球心O到截面的距离d最大即可.
此时过E的截面垂直于OE,
截面半径,
所以截面面积,
故选:C.
二.填空题
9.【解答】解:正三棱锥V﹣ABC中,侧棱长VA=2,底面三角形的边长AC,
可得底面三角形的高为:,
V到底面的距离:;
该三棱锥的侧视图的面积:.
故答案为:.
10.【解答】解:根据几何体的三视图转换为直观图为:
该几何体为由一个三棱柱和一个四棱锥构成的组合体.
如图所示:
故.
故答案为:.
11.【解答】解:由题意可知几何体是圆锥,底面半径为1,高为,母线为:2.
所以几何体的侧面积为:2π,
故答案为:2π.
12.【解答】解:由题意可知几何体是一个棱长为2正方体与一个底面是正三角形,一个侧面与在正方体的侧面的三棱锥组成,几何体的直观图如图:
所以侧视图的面积为:2×24.
几何体的体积为:2×2×28.
故答案为:4;8.
13.【解答】解:根据几何体的三视图转换为直观图为:由一个三棱锥体和一个圆锥组成的几何体.
如图所示:V.
所以表面积为:S底+S侧.
故答案为:;.
14.【解答】解:由三视图还原原几何体如图,
该几何体为组合体,下半部分为长方体,底面是边长为2的正方体,高为1,
上半部分为四分之一圆锥,圆锥的底面半径为3,高为2.
则该几何体的体积Vcm3,
由已知求得圆锥的母线长为.
连接图中PM,求得PM,设PM交长方体上底面于N,
由相似三角形对应边成比例可得PN,
则A,B分别与P,M重合时,满足AB全部在该几何体内部,且AB长度最大为cm.
故答案为:9;.
15.【解答】解:由三视图还原原几何体如图,
该几何体为三棱锥P﹣ABC,底面三角形ABC为直角三角形,
AB⊥BC,AB=3,BC=4,三棱锥的高为PD=3.
则其体积V;
把该三棱锥补形为长方体,则其外接球的半径R.
∴其外接球的表面积S.
故答案为:6;34π.
三.解答题
16.【解答】解:(1)以同样大的几何体,进行补形,可得一直三棱柱,
其底面为△A1B1C1,高为3×2=6,
∴所求几何体的体积为
Vh2×2×6=6;
(2)△ABC中,AB,
BC,
AC2,
∴△ABC为等腰三角形,底边AC的高为:
h;
∴截面ABC的面积为
S△ABC2.
17.【解答】解:由三视图可知,该几何体是由半球和正四棱柱组成,棱柱是正方体棱长为:2,球的半径为1,
(1)该几何体的表面积=正方体的表面积+半球面面积﹣球的底面积.
∴S=6×2×2+2π×12﹣π×12=24+π(m2).
(2)该几何体的体积为正方体的体积+半球的体积,
V=2×2×2π×13=8π(m3)
18.【解答】解:根据几何体的三视图转换为几何体为:该几何体为四棱柱.
如图所示:
所以:V,
所以该几何体的体积为3.
19.【解答】解:(1)由三视图知,该三视图对应的几何体为一个底面直径为2,母线长为2的圆锥与一个长宽都为2高为1的长方体组成的组合体.(2分)
(2)此几何体的表面积:S=2π+2×4﹣π+4×2=π+16(6分)
此几何体的体积:Vπ+4(10分)
20.【解答】解:由已知中的三视图,可得:该几何体是一个长方体挖去一个圆柱所得的组合体,
长方体的长宽高分别为4,3,1,
故长方体的体积为:12,
圆柱的底面半径为1,高为1,
故圆柱的体积为:π,
故组合体的体积为:12﹣π,
长方体的表面积为:2(1×3+1×4+3×4)=38,
圆柱的底面积为π,
侧面积为:2π,
故几何体的表面积为:38﹣2π+2π=38.
21.【解答】解:由三视图可知该几何体是由上下两部分组成:上面是直径为2的球;下面是一个长方体,其长宽高分别为2,2,3,且球切于长方体上底面的圆心.
∴S表面积=4π×12+2×(2×2+2×3+2×3)=4π+32.
V体积π×13+2×2×312.
22.【解答】解:由三视图知几何体是一个组合体,下半部是长方体,上半部是半圆柱,
其轴截面的大小与长方体的上底面大小一致.
长方体的棱长分别是4,6,8
圆柱的高是8,底面圆的半径是2
∴表面积为S=32+96+48+4π+16π=176+20π,
体积为V=192+16π,
即几何体的表面积为176+20πcm2,体积为192+16πcm3
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
