山东省烟台招远市五四制2021届九年级上期末考试数学试题(word版含答案)
文档属性
| 名称 | 山东省烟台招远市五四制2021届九年级上期末考试数学试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 315.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 13:27:58 | ||
图片预览




文档简介
2020-2021学年度第一学期期末考试初四数学试卷
说明:1.
考试时间120分钟,满分120分。
2.
考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.已知∠α为锐角,且sinα=,则∠α=( )
A.30°
B.45°
C.60°
D.90°
2.平面内,⊙O的半径为1,点P到O的距离为3,过点P可作⊙O的切线条数为( )
A.0条
B.1条
C.2条
D.无数条
3.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A.
B.
C.
D.
4.一人乘雪橇沿坡比1:的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为5s,则此人下降的高度为( )
A.90m
B.45m
C.45m
D.90m
5.如图,AB是⊙O直径,若∠AOC=150°,则∠D的度数是( )
A.15°
B.25°
C.30°
D.75°
6.二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=2
C.顶点坐标为(-2,4)
D.当x<﹣2时,y随x的增大而增大
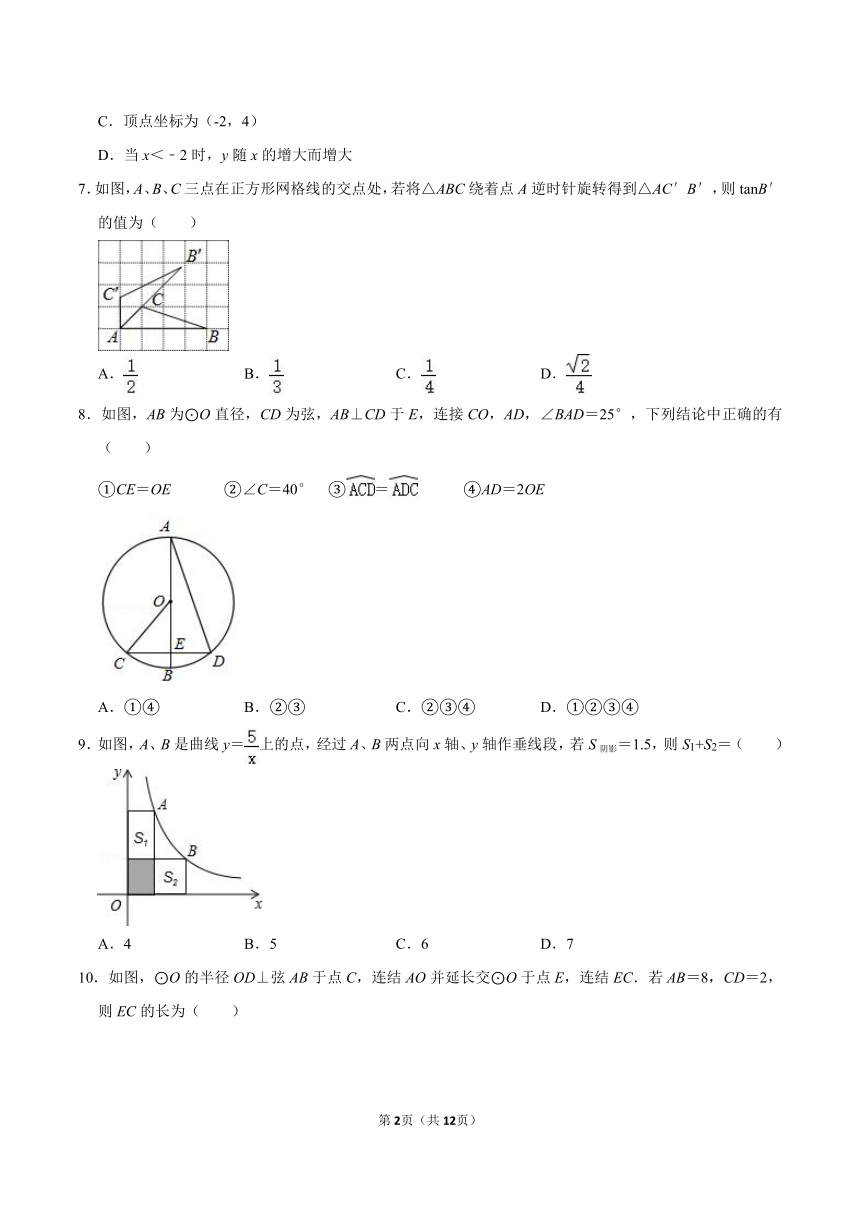
7.如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
8.如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=25°,下列结论中正确的有( )
①CE=OE
②∠C=40°
③=
④AD=2OE
A.①④
B.②③
C.②③④
D.①②③④
9.如图,A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1.5,则S1+S2=( )
A.4
B.5
C.6
D.7
10.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2
B.2
C.2
D.8
11.如图,抛物线y=﹣x2+2x+2交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.下列说法:其中正确判断的序号是( )
①抛物线与直线y=3有且只有一个交点;
②若点M(﹣2,y1),N(1,y2),P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线先向左,再向下均平移2个单位,所得抛物线解析式为y=﹣(x+1)2+1;
④在x轴上找一点D,使AD+BD的和最小,则最小值为.
A.①②④
B.①②③
C.①③④
D.②③④
12.如图,抛物线y=x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是( )
A.3
B.
C.
D.4
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.函数y=中的自变量x的取值范围________
14.正六边形的半径长与边心距的比值等于
.
15.若二次函数y=x2-(m-1)x的图像经过点(3,0),则关于x的一元二次方程x2-(m-1)x=0的根为_________
16.半径为5的圆内有长为5的弦,则此弦所对的圆周角为_______
17.如图,⊙O是△ABC的内切圆,与边BC,CA,AB的切点分别为D,E,F,若∠A=70°,则∠EDF=
度.
18.如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为
.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.计算:
(1)2sin30°+3cos60°+tan45°;
(2)﹣|﹣3|+()﹣2﹣4cos30°.
20.文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了
名学生;
(2)最喜爱《朗读者》的学生有
名;
(3)扇形统计图中“B”所在扇形圆心角的度数为
;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请求出:刚好选到一名男生和一名女生的概率.
21.如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.
22.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元,市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
23.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上(A、H、F近似的看成在一条直线上),篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
24.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2019/11/30
23:17:53;用户:15330278117;邮箱:15330278117;学号27.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的表达式;
(2)如图1,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(3)如图2,在x轴上是否存在一点D,使得△ACD为等腰三角形?若存在,请直接写出所有符合条件的点D的坐标;若不存在,请说明理由.
参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.A
2.C
3.A
4.B
5.A
6.D
7.B
8.B
9.D
10.B
11.C
12.
C
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.x且x
14.
15.
x1=0
16.
60°或120°
17.55°
18.1
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
三.解答题(共8小题)
19.
解:(1)原式=2×+3×+1
=1++1
=;
.................................................................................................4分
(2)﹣|﹣3|+()﹣2﹣4cos30°
=2﹣3+4﹣4×
=2﹣3+4﹣2
=1.
..............................................................................8分
解:(1)150;
...........................................................................1分
(2)75
..........................................................................2分
(3)36°;
..........................................................................4分
(4)记选择“E”的同学中的2名女生分别为N1,N2,4名男生分别为M1,M2,M3,M4,
列表如下:
N1
N2
M1
M2
M3
M4
N1
(N1,N2)
(N1,M1)
(N1,M2)
(N1,M3)
(N1,M4)
N2
(N2,N1)
(N2,M1)
(N2,M2)
(N2,M3)
(N2,M4)
M1
(M1,N1)
(M1,N2)
(M1,M2)
(M1,M3)
(M1,M4)
M2
(M2,N1)
(M2,N2)
(M2,M1)
(M2,M3)
(M2,M4)
M3
(M3,N1)
(M3,N2)
(M3,M1)
(M3,M2)
(M3,M4)
M4
(M4,N1)
(M4,N2)
(M4,M1)
(M4,M2)
(M4,M3)
∵共有30种等可能的结果,其中,刚好选到一名男生和一名女生的有16种情况,
∴P(一名男生和一名女生)==;..........................................................................8分
21.解:(1)直线BC与⊙O相切;
理由:连结OD
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵直线BC过半径OD的外端,
∴直线BC与⊙O相切.
.............................................4分
(2)连接OD,
在Rt△ODB中,∠B=30°,
∴∠BOD=60°.
∴.
∵∠B=30°,OD⊥BC,
∴tan∠B=,
∴BD=
=
=,
S△BOD=×OD?BD=18,
∴所求图形面积为18-6π
.............................................8分
22.解:(1)w=(x﹣30)?y
=(﹣x+60)(x﹣30)
=﹣x2+30x+60x﹣1800
=﹣x2+90x﹣1800,
w与x之间的函数解析式:w=﹣x2+90x﹣1800;.............................................4分
(2)根据题意得:w=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
当x=45时,w有最大值,最大值是225元..............................................6分
(3)当w=200时,﹣x2+90x﹣1800=200,
解得x1=40,x2=50,
∵50>42,x2=50不符合题意,舍去,.............................................9分
答:该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元..
............................................10分
23.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;............4分
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴sin45°=
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米..............................................10分
解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A=90?,
∠DGB=∠HDG+∠C=90?,
∴∠A=∠C.
.............................................5分
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴∠A+∠C+θ=180°.
.............................................10分
25.解:(1)将点A(1,0),B(﹣3,0)代入y=ax2+bx+3,
得,,
解得,,
∴抛物线表达式为y=﹣x2﹣2x+3;.............................................3分
(2)如图1,过点E作EF⊥x轴于点F,
设E(a,﹣a2﹣2a+3)
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴
=
=
=,
∴当时,S四边形BOCE最大,且最大值为;
当时,,
此时,点E坐标为;.............................................8分
(3)存在符合条件的点D,其坐标为D1(﹣1,0)或或或D4(﹣4,0).
.............................................12分
第12页(共12页)
说明:1.
考试时间120分钟,满分120分。
2.
考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.已知∠α为锐角,且sinα=,则∠α=( )
A.30°
B.45°
C.60°
D.90°
2.平面内,⊙O的半径为1,点P到O的距离为3,过点P可作⊙O的切线条数为( )
A.0条
B.1条
C.2条
D.无数条
3.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )
A.
B.
C.
D.
4.一人乘雪橇沿坡比1:的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为5s,则此人下降的高度为( )
A.90m
B.45m
C.45m
D.90m
5.如图,AB是⊙O直径,若∠AOC=150°,则∠D的度数是( )
A.15°
B.25°
C.30°
D.75°
6.二次函数y=﹣2(x+2)2﹣4,下列说法正确的是( )
A.开口向上
B.对称轴为直线x=2
C.顶点坐标为(-2,4)
D.当x<﹣2时,y随x的增大而增大
7.如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为( )
A.
B.
C.
D.
8.如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=25°,下列结论中正确的有( )
①CE=OE
②∠C=40°
③=
④AD=2OE
A.①④
B.②③
C.②③④
D.①②③④
9.如图,A、B是曲线y=上的点,经过A、B两点向x轴、y轴作垂线段,若S阴影=1.5,则S1+S2=( )
A.4
B.5
C.6
D.7
10.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2
B.2
C.2
D.8
11.如图,抛物线y=﹣x2+2x+2交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.下列说法:其中正确判断的序号是( )
①抛物线与直线y=3有且只有一个交点;
②若点M(﹣2,y1),N(1,y2),P(2,y3)在该函数图象上,则y1<y2<y3;
③将该抛物线先向左,再向下均平移2个单位,所得抛物线解析式为y=﹣(x+1)2+1;
④在x轴上找一点D,使AD+BD的和最小,则最小值为.
A.①②④
B.①②③
C.①③④
D.②③④
12.如图,抛物线y=x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是( )
A.3
B.
C.
D.4
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.函数y=中的自变量x的取值范围________
14.正六边形的半径长与边心距的比值等于
.
15.若二次函数y=x2-(m-1)x的图像经过点(3,0),则关于x的一元二次方程x2-(m-1)x=0的根为_________
16.半径为5的圆内有长为5的弦,则此弦所对的圆周角为_______
17.如图,⊙O是△ABC的内切圆,与边BC,CA,AB的切点分别为D,E,F,若∠A=70°,则∠EDF=
度.
18.如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为
.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.计算:
(1)2sin30°+3cos60°+tan45°;
(2)﹣|﹣3|+()﹣2﹣4cos30°.
20.文化是一个国家、一个民族的灵魂,近年来,央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况,某学校组织学生会成员随机抽取了部分学生进行调查,被调查的学生必须从《经曲咏流传》(记为A)、《中国诗词大会》(记为B)、《中国成语大会》(记为C)、《朗读者》(记为D)中选择自己最喜爱的一个栏目,也可以不选以上四类而写出一个自己最喜爱的其他文化栏目(这时记为E).根据调查结果绘制成如图所示的两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)在这项调查中,共调查了
名学生;
(2)最喜爱《朗读者》的学生有
名;
(3)扇形统计图中“B”所在扇形圆心角的度数为
;
(4)选择“E”的学生中有2名女生,其余为男生,现从选择“E”的学生中随机选出两名学生参加座谈,请求出:刚好选到一名男生和一名女生的概率.
21.如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.
22.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个30元,市场调查发现,这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于42元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
23.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上(A、H、F近似的看成在一条直线上),篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
24.已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且=.
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
(2)如图②,若的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2019/11/30
23:17:53;用户:15330278117;邮箱:15330278117;学号27.如图1,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的表达式;
(2)如图1,若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(3)如图2,在x轴上是否存在一点D,使得△ACD为等腰三角形?若存在,请直接写出所有符合条件的点D的坐标;若不存在,请说明理由.
参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.A
2.C
3.A
4.B
5.A
6.D
7.B
8.B
9.D
10.B
11.C
12.
C
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.x且x
14.
15.
x1=0
16.
60°或120°
17.55°
18.1
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
三.解答题(共8小题)
19.
解:(1)原式=2×+3×+1
=1++1
=;
.................................................................................................4分
(2)﹣|﹣3|+()﹣2﹣4cos30°
=2﹣3+4﹣4×
=2﹣3+4﹣2
=1.
..............................................................................8分
解:(1)150;
...........................................................................1分
(2)75
..........................................................................2分
(3)36°;
..........................................................................4分
(4)记选择“E”的同学中的2名女生分别为N1,N2,4名男生分别为M1,M2,M3,M4,
列表如下:
N1
N2
M1
M2
M3
M4
N1
(N1,N2)
(N1,M1)
(N1,M2)
(N1,M3)
(N1,M4)
N2
(N2,N1)
(N2,M1)
(N2,M2)
(N2,M3)
(N2,M4)
M1
(M1,N1)
(M1,N2)
(M1,M2)
(M1,M3)
(M1,M4)
M2
(M2,N1)
(M2,N2)
(M2,M1)
(M2,M3)
(M2,M4)
M3
(M3,N1)
(M3,N2)
(M3,M1)
(M3,M2)
(M3,M4)
M4
(M4,N1)
(M4,N2)
(M4,M1)
(M4,M2)
(M4,M3)
∵共有30种等可能的结果,其中,刚好选到一名男生和一名女生的有16种情况,
∴P(一名男生和一名女生)==;..........................................................................8分
21.解:(1)直线BC与⊙O相切;
理由:连结OD
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵直线BC过半径OD的外端,
∴直线BC与⊙O相切.
.............................................4分
(2)连接OD,
在Rt△ODB中,∠B=30°,
∴∠BOD=60°.
∴.
∵∠B=30°,OD⊥BC,
∴tan∠B=,
∴BD=
=
=,
S△BOD=×OD?BD=18,
∴所求图形面积为18-6π
.............................................8分
22.解:(1)w=(x﹣30)?y
=(﹣x+60)(x﹣30)
=﹣x2+30x+60x﹣1800
=﹣x2+90x﹣1800,
w与x之间的函数解析式:w=﹣x2+90x﹣1800;.............................................4分
(2)根据题意得:w=﹣x2+90x﹣1800=﹣(x﹣45)2+225,
∵﹣1<0,
当x=45时,w有最大值,最大值是225元..............................................6分
(3)当w=200时,﹣x2+90x﹣1800=200,
解得x1=40,x2=50,
∵50>42,x2=50不符合题意,舍去,.............................................9分
答:该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为40元..
............................................10分
23.解:(1)在Rt△EFH中,cos∠FHE==,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;............4分
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴sin45°=
∴HN=AHsin45°=×=,
∴EM=EG+GM=+,
答:篮板底部点E到地面的距离是(+)米..............................................10分
解:(1)连接DF、DG.
∵BD是⊙O的直径,
∴∠DFB=∠DGB=90°,
∵=,
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A=90?,
∠DGB=∠HDG+∠C=90?,
∴∠A=∠C.
.............................................5分
(2)结论:α+β+θ=180°.
理由:如图②中,连接DF,BH.
∵=,
∴∠ADF=∠HBG=θ,
∵∠A+∠ADF+∠AFD=180°,∠AFD=∠DHB=∠C+∠HBG,
∴∠A+θ+∠C+θ=180°,
∴∠A+∠C+θ=180°.
.............................................10分
25.解:(1)将点A(1,0),B(﹣3,0)代入y=ax2+bx+3,
得,,
解得,,
∴抛物线表达式为y=﹣x2﹣2x+3;.............................................3分
(2)如图1,过点E作EF⊥x轴于点F,
设E(a,﹣a2﹣2a+3)
∴EF=﹣a2﹣2a+3,BF=a+3,OF=﹣a,
∴
=
=
=,
∴当时,S四边形BOCE最大,且最大值为;
当时,,
此时,点E坐标为;.............................................8分
(3)存在符合条件的点D,其坐标为D1(﹣1,0)或或或D4(﹣4,0).
.............................................12分
第12页(共12页)
同课章节目录
