山东省烟台招远市五四制2020-2021学年七年级上期末考试数学试题(word版含答案)
文档属性
| 名称 | 山东省烟台招远市五四制2020-2021学年七年级上期末考试数学试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 13:34:21 | ||
图片预览



文档简介
2020-2021学年度第一学期期末考试初二数学试卷
说明:1.
考试时间120分钟,满分120分。
2.
考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.在实数:π,,,2π,,0.36,0.3737737773…(相邻两个3之间7的个数逐次加1),﹣,,无理数的个数为( )
A.4
B.5
C.7
D.9
2.下列曲线中不能表示y是x的函数的是( )
A.
B.
C.
D.
3.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A.
B.
C.
D.
4.下列判断:
①一个数的平方根等于它本身,这个数是0和1;
②实数包括无理数和有理数;
③2的算术平方根是;
④无理数是带根号的数.
正确的有( )
A.1个
B.2个
C.3个
D.4个
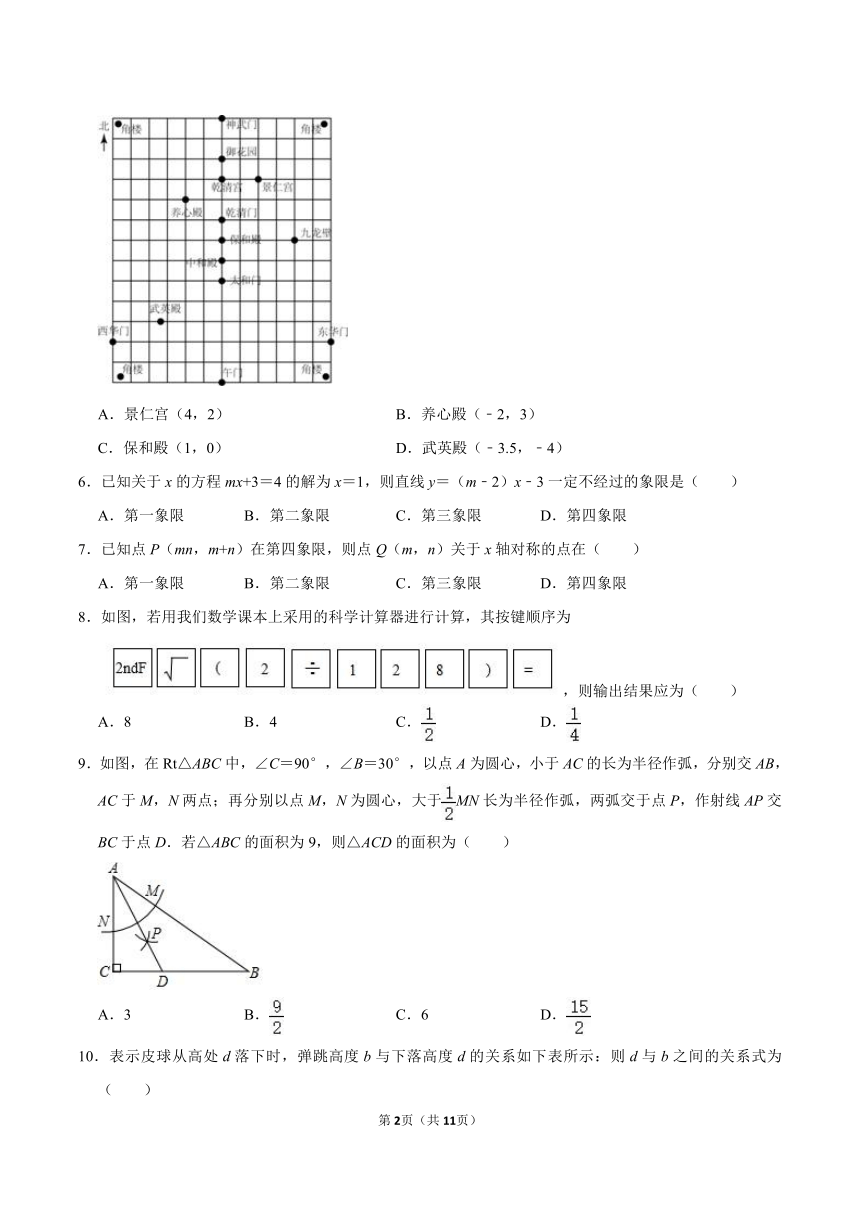
5.如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2)?
B.养心殿(﹣2,3)
C.保和殿(1,0)
D.武英殿(﹣3.5,﹣4)
6.已知关于x的方程mx+3=4的解为x=1,则直线y=(m﹣2)x﹣3一定不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知点P(mn,m+n)在第四象限,则点Q(m,n)关于x轴对称的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.如图,若用我们数学课本上采用的科学计算器进行计算,其按键顺序为
,则输出结果应为( )
A.8
B.4
C.
D.
9.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径作弧,分别交AB,AC于M,N两点;再分别以点M,N为圆心,大于MN长为半径作弧,两弧交于点P,作射线AP交BC于点D.若△ABC的面积为9,则△ACD的面积为( )
A.3
B.
C.6
D.
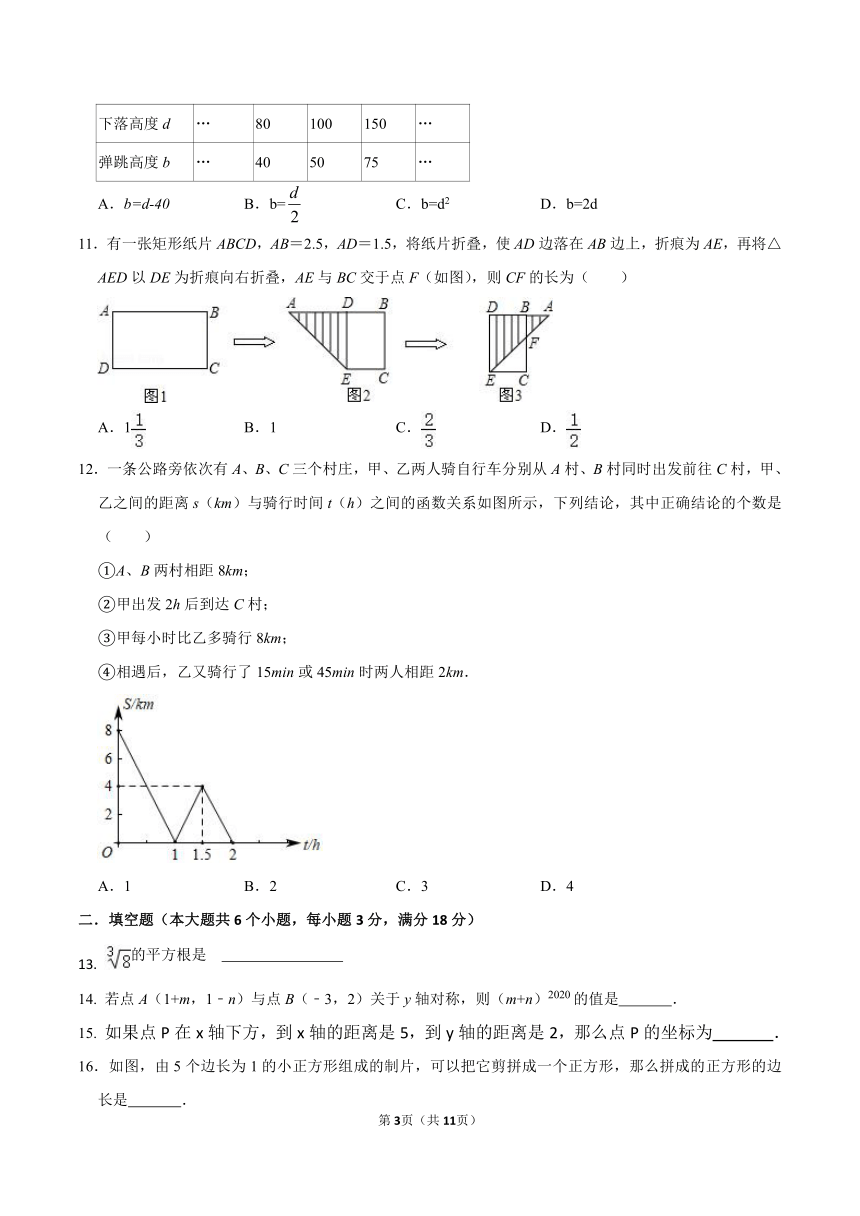
10.表示皮球从高处d落下时,弹跳高度b与下落高度d的关系如下表所示:则d与b之间的关系式为( )
下落高度d
…
80
100
150
…
弹跳高度b
…
40
50
75
…
A.b=d-40
B.b=
C.b=d2
D.b=2d
11.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为( )
A.1
B.1
C.
D.
12.一条公路旁依次有A、B、C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论,其中正确结论的个数是( )
①A、B两村相距8km;
②甲出发2h后到达C村;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或45min时两人相距2km.
A.1
B.2
C.3
D.4
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.
的平方根是
14.
若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则(m+n)2020的值是
.
15.
如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为
.
16.如图,由5个边长为1的小正方形组成的制片,可以把它剪拼成一个正方形,那么拼成的正方形的边长是
.
17.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:
t(小时)
0
1
2
3
y(升)
120
112
104
96
由表格中y与t的关系可知,当汽车行驶
小时,油箱的余油量为0.
18.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是
.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.计算:
(1)﹣12+﹣(﹣2)×
(2)(+1)+|﹣2|
20.如图,在12×10的正方形网格中,△ABC是格点三角形,点B的坐标为(﹣5,1),点C的坐标为(﹣4,5).
(1)请在方格纸中画出x轴、y轴,并标出原点O;
(2)画出△ABC关于直线l对称的△A1B1C1;C1的坐标为
(3)若点P(a,b)在△ABC内,其关于直线l的对称点是P1,则P1的坐标是
.
21.科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系.经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)已知某山的海拔高度为1200米,请你求出该山山顶处的空气含氧量约为多少?
22.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
23.如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,3),且与正比例函数y=x的图象交于点C(m,6).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
24.已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°
(1)若D为△ACB内部一点,如图,AE=BD吗?说明理由
(2)若D为AB边上一点,AD=5,BD=12,求DE的长
25.(11分)如图,l1表示振华商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系.观察图象,解决以下问题:
(1)当销售量x=2时,
销售额=
万元,销售成本=
万元;
(2)一天销售
台时,销售额等于销售成本;当销售量
时,该商场实现赢利(收入大于成本);
(3)分别求出l1和l2对应的函数表达式;
(4)直接写出利润w与销售量x之间的函数表达式,并求出当销售量x是多少时,每天的利润达到5万元?
初二数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.A
2.D
3.C
4.B
5.B
6.A
7.B
8.D
9.A
10.B
11.B
12.
C
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.
14.1
15.(2,-5)或(-2,-5)
16.
17.15
18.45?
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解:(1)原式=﹣1+(﹣3)+2×3
=﹣1﹣3+6
=2;
……………………………………………4分
(2)原式=3++2﹣
=5.
……………………………………………4分
20.解:(1)如图,就是所求作的坐标轴与原点………………………………………2分
(2)如图,△A1B1C1为所作的三角形;(0,5)……………………………………………6
(3)P1的坐标是(﹣a﹣4,b).
……………………………………………8
21.解:(1)设要求的表达式为y=kx+b(k≠0),……………………………………………1
由题可知:当x=0时,y=299
∴299=b
∴
y=kx+299
当x=2000时,y=235,
235=2000k+299
K=-=-
∴y=﹣x+299;
……………………………………………5
(2)当x=1200时,y=﹣×1200+299=260.6(克/立方米).
答:该山山顶处的空气含氧量约为260.6克/立方米.……………8
22.
解:(1)兔子,1500;……………………………………………2
(2)结合图象得出:兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
……………………………………………4
(3)700÷30=(分钟),
答:乌龟用了分钟追上了正在睡觉的兔子.………………………7
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴50+0.5﹣2﹣2=46.5(分钟).
答:兔子中间停下睡觉用了46.5分钟.……………………10
23.
解:(1)AE=BD,AE⊥BD
……………………………………………1
理由如下:∵△ACB和△ECD都是等腰直角三角形,
∴CD=CE,AC=BC,∠ECD=∠ACB=90°,
∴∠ACE=∠BCD
在△ACE和△BCD中
EC=CD
∠ACE=∠BCD
AC=BC
∴△ACE≌△BCD(SAS)
∴AE=BD;
∠ECA=∠D
BC
延长BD交AE于M,交AC于N
∠ANM=∠BNC
∴∠AMN=∠BCN=90°
∴BD⊥AE
∴AE=BD,AE⊥BD
……………………………………………6分
(2)如图,
由(1)可知:△ACE≌△BCD,
∴BD=AE=12,∠CAE=∠CBD=45°,
∴∠EAD=90°,在Rt△ADE中,AE2+AD2=ED2,
,即52+122=ED2
∴DE===13.……………………………………………10
24.
解:(1)∵点C(m,6)在正比例函数y=x图象上,
∴3=m,得m=4,
∴点C的坐标为(4,6)……………………………………………2
把点B(0,3)代入y=kx+b中,得:b=3
∴一次函数的解析式为:y=kx+3;
把点C(4,6)代入y=kx+3中,得:6=4k+3
k=
y=x+3
……………………………………………4
(2)过点C作CM
x轴
在一次函数y=x+2中,令y=0,则x+2=0,解得x=﹣4,
∴点A的坐标为(﹣4,0)
即OA=4,
∵点C的坐标为(4,6)
∴
CM=6
∴S△AOC=×OA×CM=×4×6=12;………………………………7
(3)M的坐标为(﹣3,7)或(﹣7,4).……………………………..3
25.
(1)2
3,…………………………………………..……2
(2)4,
大于4台;………………………………4
(3)设l1的表达式为.将(4,4)代入得:,得,,
所以l1的表达式为
…………………………………………………………………6
设l2的表达式为.
将(0,2),(4,4)分别代入上式,得,
所以
l2的表达式为
……………………………………………….………………8
(4)利润w与销售量x之间的函数表达式为
………………………………10
令w=5时,,
解得x=14
答:当销售量x是14台时,每天的利润达到5万元……………………………………12
第11页(共11页)
说明:1.
考试时间120分钟,满分120分。
2.
考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.在实数:π,,,2π,,0.36,0.3737737773…(相邻两个3之间7的个数逐次加1),﹣,,无理数的个数为( )
A.4
B.5
C.7
D.9
2.下列曲线中不能表示y是x的函数的是( )
A.
B.
C.
D.
3.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A.
B.
C.
D.
4.下列判断:
①一个数的平方根等于它本身,这个数是0和1;
②实数包括无理数和有理数;
③2的算术平方根是;
④无理数是带根号的数.
正确的有( )
A.1个
B.2个
C.3个
D.4个
5.如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,﹣1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
A.景仁宫(4,2)?
B.养心殿(﹣2,3)
C.保和殿(1,0)
D.武英殿(﹣3.5,﹣4)
6.已知关于x的方程mx+3=4的解为x=1,则直线y=(m﹣2)x﹣3一定不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知点P(mn,m+n)在第四象限,则点Q(m,n)关于x轴对称的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.如图,若用我们数学课本上采用的科学计算器进行计算,其按键顺序为
,则输出结果应为( )
A.8
B.4
C.
D.
9.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径作弧,分别交AB,AC于M,N两点;再分别以点M,N为圆心,大于MN长为半径作弧,两弧交于点P,作射线AP交BC于点D.若△ABC的面积为9,则△ACD的面积为( )
A.3
B.
C.6
D.
10.表示皮球从高处d落下时,弹跳高度b与下落高度d的关系如下表所示:则d与b之间的关系式为( )
下落高度d
…
80
100
150
…
弹跳高度b
…
40
50
75
…
A.b=d-40
B.b=
C.b=d2
D.b=2d
11.有一张矩形纸片ABCD,AB=2.5,AD=1.5,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F(如图),则CF的长为( )
A.1
B.1
C.
D.
12.一条公路旁依次有A、B、C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论,其中正确结论的个数是( )
①A、B两村相距8km;
②甲出发2h后到达C村;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或45min时两人相距2km.
A.1
B.2
C.3
D.4
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.
的平方根是
14.
若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则(m+n)2020的值是
.
15.
如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为
.
16.如图,由5个边长为1的小正方形组成的制片,可以把它剪拼成一个正方形,那么拼成的正方形的边长是
.
17.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:
t(小时)
0
1
2
3
y(升)
120
112
104
96
由表格中y与t的关系可知,当汽车行驶
小时,油箱的余油量为0.
18.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是
.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.计算:
(1)﹣12+﹣(﹣2)×
(2)(+1)+|﹣2|
20.如图,在12×10的正方形网格中,△ABC是格点三角形,点B的坐标为(﹣5,1),点C的坐标为(﹣4,5).
(1)请在方格纸中画出x轴、y轴,并标出原点O;
(2)画出△ABC关于直线l对称的△A1B1C1;C1的坐标为
(3)若点P(a,b)在△ABC内,其关于直线l的对称点是P1,则P1的坐标是
.
21.科学研究发现,空气含氧量y(克/立方米)与海拔高度x(米)之间近似地满足一次函数关系.经测量,在海拔高度为0米的地方,空气含氧量约为299克/立方米;在海拔高度为2000米的地方,空气含氧量约为235克/立方米.
(1)求出y与x的函数表达式;
(2)已知某山的海拔高度为1200米,请你求出该山山顶处的空气含氧量约为多少?
22.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
23.如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,3),且与正比例函数y=x的图象交于点C(m,6).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
24.已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°
(1)若D为△ACB内部一点,如图,AE=BD吗?说明理由
(2)若D为AB边上一点,AD=5,BD=12,求DE的长
25.(11分)如图,l1表示振华商场一天的某型电脑销售额与销售量的关系,l2表示该商场一天的销售成本与电脑销售量的关系.观察图象,解决以下问题:
(1)当销售量x=2时,
销售额=
万元,销售成本=
万元;
(2)一天销售
台时,销售额等于销售成本;当销售量
时,该商场实现赢利(收入大于成本);
(3)分别求出l1和l2对应的函数表达式;
(4)直接写出利润w与销售量x之间的函数表达式,并求出当销售量x是多少时,每天的利润达到5万元?
初二数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.A
2.D
3.C
4.B
5.B
6.A
7.B
8.D
9.A
10.B
11.B
12.
C
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.
14.1
15.(2,-5)或(-2,-5)
16.
17.15
18.45?
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解:(1)原式=﹣1+(﹣3)+2×3
=﹣1﹣3+6
=2;
……………………………………………4分
(2)原式=3++2﹣
=5.
……………………………………………4分
20.解:(1)如图,就是所求作的坐标轴与原点………………………………………2分
(2)如图,△A1B1C1为所作的三角形;(0,5)……………………………………………6
(3)P1的坐标是(﹣a﹣4,b).
……………………………………………8
21.解:(1)设要求的表达式为y=kx+b(k≠0),……………………………………………1
由题可知:当x=0时,y=299
∴299=b
∴
y=kx+299
当x=2000时,y=235,
235=2000k+299
K=-=-
∴y=﹣x+299;
……………………………………………5
(2)当x=1200时,y=﹣×1200+299=260.6(克/立方米).
答:该山山顶处的空气含氧量约为260.6克/立方米.……………8
22.
解:(1)兔子,1500;……………………………………………2
(2)结合图象得出:兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
……………………………………………4
(3)700÷30=(分钟),
答:乌龟用了分钟追上了正在睡觉的兔子.………………………7
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴50+0.5﹣2﹣2=46.5(分钟).
答:兔子中间停下睡觉用了46.5分钟.……………………10
23.
解:(1)AE=BD,AE⊥BD
……………………………………………1
理由如下:∵△ACB和△ECD都是等腰直角三角形,
∴CD=CE,AC=BC,∠ECD=∠ACB=90°,
∴∠ACE=∠BCD
在△ACE和△BCD中
EC=CD
∠ACE=∠BCD
AC=BC
∴△ACE≌△BCD(SAS)
∴AE=BD;
∠ECA=∠D
BC
延长BD交AE于M,交AC于N
∠ANM=∠BNC
∴∠AMN=∠BCN=90°
∴BD⊥AE
∴AE=BD,AE⊥BD
……………………………………………6分
(2)如图,
由(1)可知:△ACE≌△BCD,
∴BD=AE=12,∠CAE=∠CBD=45°,
∴∠EAD=90°,在Rt△ADE中,AE2+AD2=ED2,
,即52+122=ED2
∴DE===13.……………………………………………10
24.
解:(1)∵点C(m,6)在正比例函数y=x图象上,
∴3=m,得m=4,
∴点C的坐标为(4,6)……………………………………………2
把点B(0,3)代入y=kx+b中,得:b=3
∴一次函数的解析式为:y=kx+3;
把点C(4,6)代入y=kx+3中,得:6=4k+3
k=
y=x+3
……………………………………………4
(2)过点C作CM
x轴
在一次函数y=x+2中,令y=0,则x+2=0,解得x=﹣4,
∴点A的坐标为(﹣4,0)
即OA=4,
∵点C的坐标为(4,6)
∴
CM=6
∴S△AOC=×OA×CM=×4×6=12;………………………………7
(3)M的坐标为(﹣3,7)或(﹣7,4).……………………………..3
25.
(1)2
3,…………………………………………..……2
(2)4,
大于4台;………………………………4
(3)设l1的表达式为.将(4,4)代入得:,得,,
所以l1的表达式为
…………………………………………………………………6
设l2的表达式为.
将(0,2),(4,4)分别代入上式,得,
所以
l2的表达式为
……………………………………………….………………8
(4)利润w与销售量x之间的函数表达式为
………………………………10
令w=5时,,
解得x=14
答:当销售量x是14台时,每天的利润达到5万元……………………………………12
第11页(共11页)
同课章节目录
