北师大版八年级数学下册1.4 角平分线课件(21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册1.4 角平分线课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 253.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 14:15:19 | ||
图片预览



文档简介
1.4
角平分线
北师大版八年级数学(下)
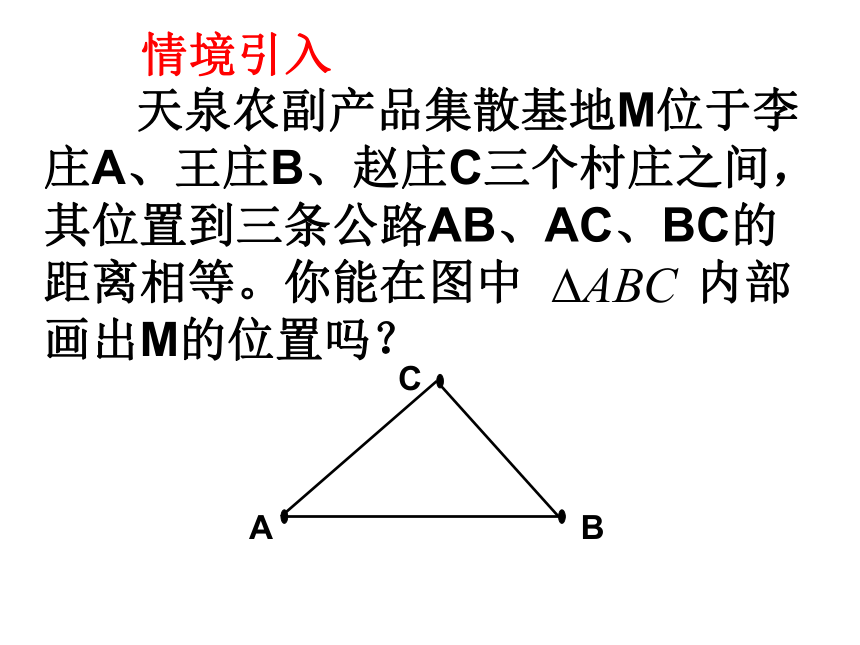
情境引入
天泉农副产品集散基地M位于李庄A、王庄B、赵庄C三个村庄之间,其位置到三条公路AB、AC、BC的距离相等。你能在图中
内部画出M的位置吗?
A
C
B
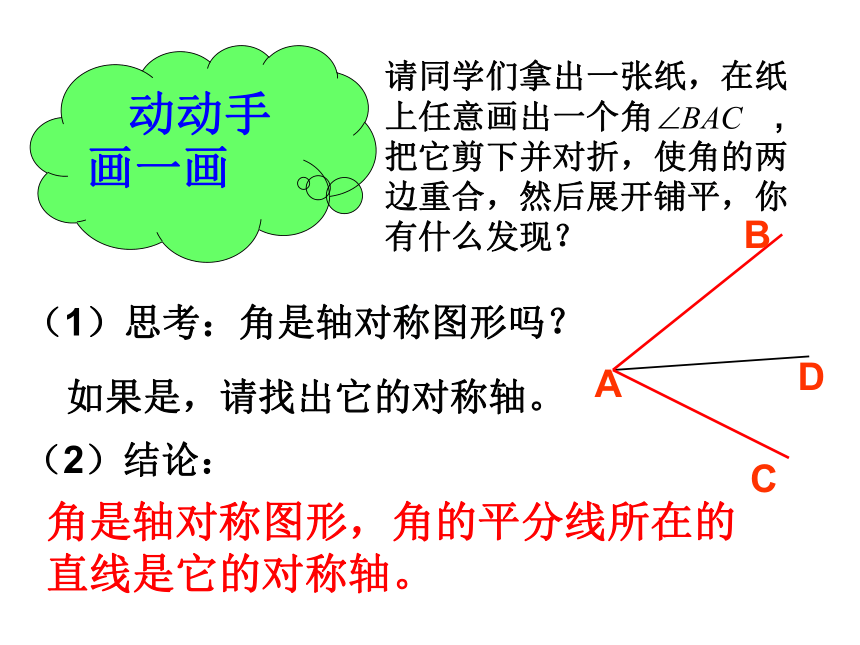
动动手画一画
请同学们拿出一张纸,在纸上任意画出一个角
,把它剪下并对折,使角的两边重合,然后展开铺平,你有什么发现?
(1)思考:角是轴对称图形吗?
如果是,请找出它的对称轴。
(2)结论:
角是轴对称图形,角的平分线所在的直线是它的对称轴。
C
D
A
B
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
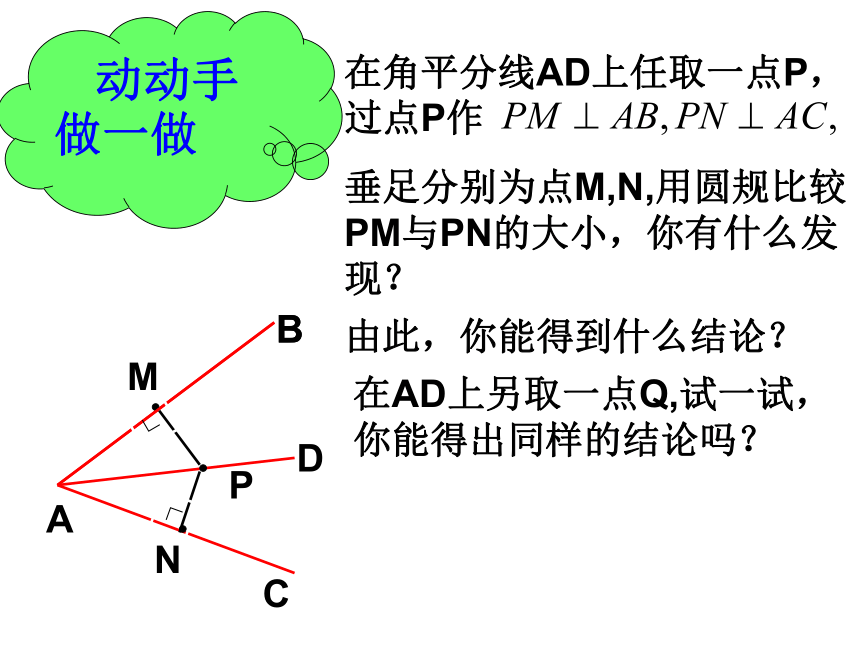
动动手做一做
在角平分线AD上任取一点P,过点P作
垂足分别为点M,N,用圆规比较PM与PN的大小,你有什么发现?
A
C
D
B
P
B
M
N
∟
∟
由此,你能得到什么结论?
在AD上另取一点Q,试一试,你能得出同样的结论吗?
角平分线的性质
角平分线上的点,到这个角的两边的距离相等。
A
C
D
B
P
B
M
N
∟
∟
已知:AD为
角平分线,P为AD上任意一点,
试说明:PM=PN
性质主要用于证明两线段相等,使用的前提是有角的平分线,关键是图中是否有“垂直”。
A
B
C
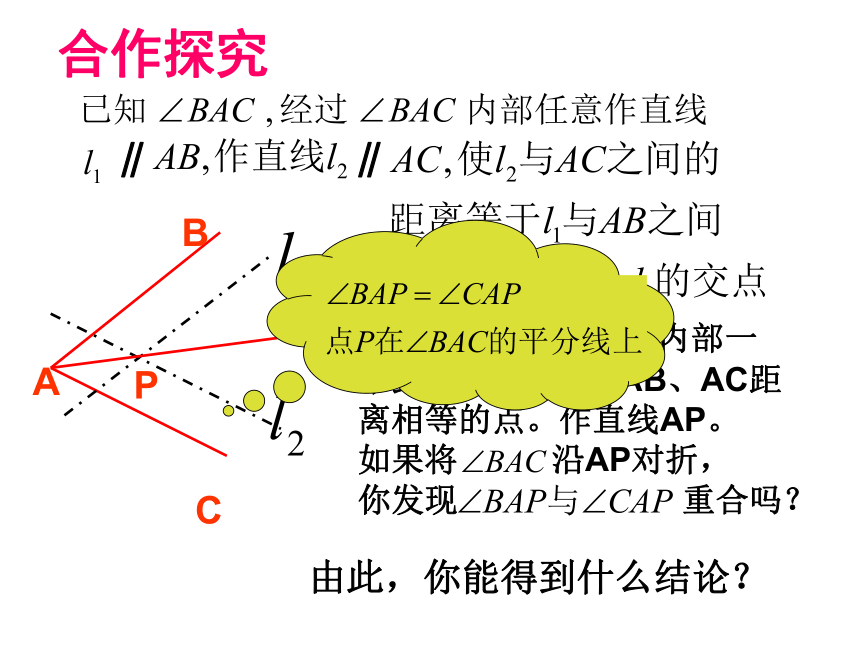
合作探究
∥
∥
则P是
内部一
个到
的两边AB、AC距
离相等的点。作直线AP。
如果将
沿AP对折,
你发现
重合吗?
由此,你能得到什么结论?
P
角平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上。
性质和判定的区别和联系:
温馨提醒
性质说明只要是角平分线上的点,它到角两边的距离一定相等,无一例外;判定反映了只要是到角两边距离相等的点,都一定在角的平分线上,而绝不会漏掉一个。
前者用来证明线段相等,后者用来证明角相等(角平分线)
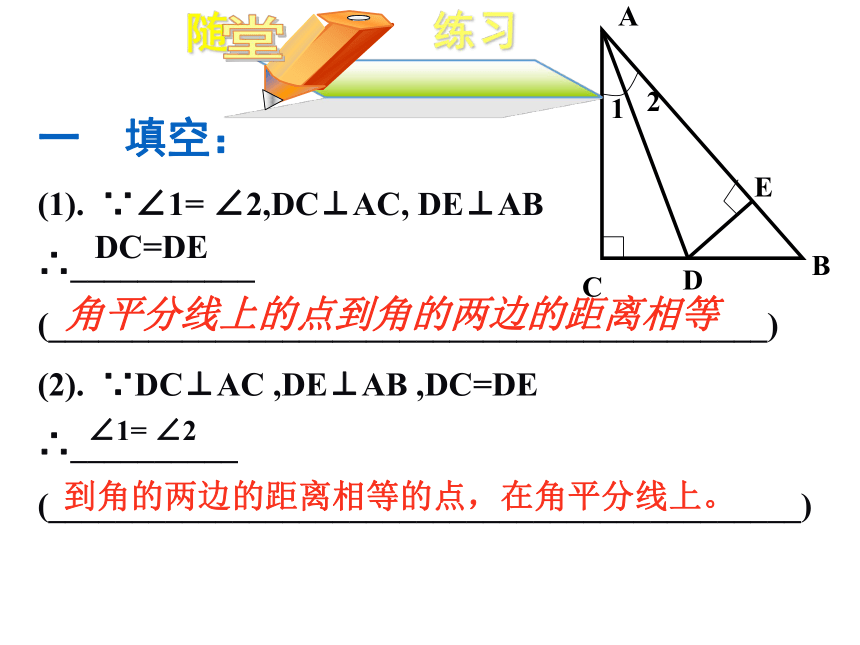
一
填空:
(1).
∵∠1=
∠2,DC⊥AC,
DE⊥AB
∴___________
(___________________________________________)
(2).
∵DC⊥AC
,DE⊥AB
,DC=DE
∴__________
(_____________________________________________)
A
C
D
E
B
1
2
∠1=
∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
堂
图1
图2
B
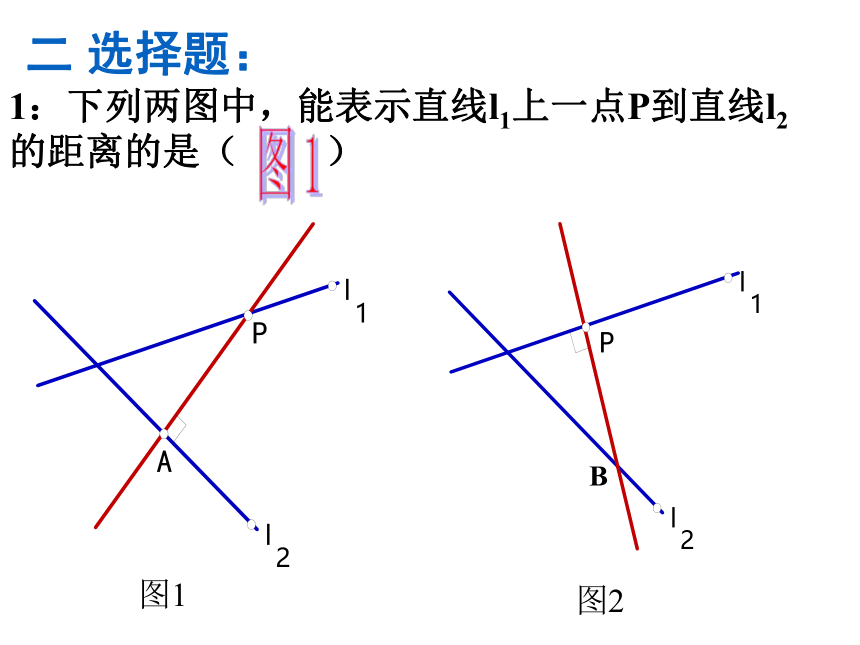
1:下列两图中,能表示直线l1上一点P到直线l2的距离的是(
)
图1
二
选择题:
2:下列两图中,能表示角的平分线上的一点P到角的边上的距离的是(
)
图1
图1
图2
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
角的平分线上的点到角的两边的距离相等。
BD
CD
三
判断:
(×)
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
角的平分线上的点到角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
角的平分线上的点到角的两边的距离相等。
√
情境引入
天泉农副产品集散基地M位于李庄A、王庄B、赵庄C三个村庄之间,其位置到三条公路AB、AC、BC的距离相等。你能在图中
内部画出M的位置吗?
A
C
B
怎样作一个角的平分线?(不用量角器)
A
B
C
P
探究新知
E
A
F
P
E
F
观察领悟作法,探索思考证明方法
已知:
∠BAC(如图)
求作:
∠BAC的角平分线OP
在△AEP和△AFP中
AE=AF
PE=PF
AP=AP
∵△AEP≌△AFP(SSS)
∴∠EAP=∠FAP
即:AP
是∠BAC的角平分线.
1、以A为圆心,适当长为半径作弧,交AB于E,交AC于F。
2、分别以E、F为圆心,大于
的长为半径作弧,两弧在∠BAC内部交于点P。
3、作射线AP,射线OP即为所求。
作法:
B
C
A
P
F
E
证明:连结PE,PC由作法知:
问题1.在上面作法的第二步中,去掉“大于
EF的长”这个条件行吗?
【答案】不行.因为去掉“大于
EF的长”这个条件,所作的两弧可能没有交点,所以就找不到角的平分线.
【答案】若分别以E、F为圆心,大于
EF的长为半径画两弧,两弧的交点可能在∠BAC的内部,也可能在∠BAC的外部,而我们要找的是∠BAC内部的交点,否则两弧交点与顶点连线得到的射线就不是∠BAC的平分线了.
问题2.第二步中所作的两弧交点一定在∠AOB的内部吗?
思考:
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺
1:20
000)
s
O
公路
铁路
解:
作夹角的角平分线OC,截取
OD=2.5cm
,D即为所求。
D
C
s
O
公路
铁路
3,在Rt三角形ACB中,AD平分
∠BAC
交BC于D,若BC=9,BD=6,求点D到AB边的距离
A
B
D
C
4、ΔABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等。
A
C
B
M
N
P
角平分线
北师大版八年级数学(下)
情境引入
天泉农副产品集散基地M位于李庄A、王庄B、赵庄C三个村庄之间,其位置到三条公路AB、AC、BC的距离相等。你能在图中
内部画出M的位置吗?
A
C
B
动动手画一画
请同学们拿出一张纸,在纸上任意画出一个角
,把它剪下并对折,使角的两边重合,然后展开铺平,你有什么发现?
(1)思考:角是轴对称图形吗?
如果是,请找出它的对称轴。
(2)结论:
角是轴对称图形,角的平分线所在的直线是它的对称轴。
C
D
A
B
PPT模板:www./moban/
PPT素材:www./sucai/
PPT背景:www./beijing/
PPT图表:www./tubiao/
PPT下载:www./xiazai/
PPT教程:
www./powerpoint/
资料下载:www./ziliao/
范文下载:www./fanwen/
试卷下载:www./shiti/
教案下载:www./jiaoan/
PPT论坛:www.
PPT课件:www./kejian/
语文课件:www./kejian/yuwen/
数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/
美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/
物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/
生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/
历史课件:www./kejian/lishi/
动动手做一做
在角平分线AD上任取一点P,过点P作
垂足分别为点M,N,用圆规比较PM与PN的大小,你有什么发现?
A
C
D
B
P
B
M
N
∟
∟
由此,你能得到什么结论?
在AD上另取一点Q,试一试,你能得出同样的结论吗?
角平分线的性质
角平分线上的点,到这个角的两边的距离相等。
A
C
D
B
P
B
M
N
∟
∟
已知:AD为
角平分线,P为AD上任意一点,
试说明:PM=PN
性质主要用于证明两线段相等,使用的前提是有角的平分线,关键是图中是否有“垂直”。
A
B
C
合作探究
∥
∥
则P是
内部一
个到
的两边AB、AC距
离相等的点。作直线AP。
如果将
沿AP对折,
你发现
重合吗?
由此,你能得到什么结论?
P
角平分线的判定:
角的内部到角的两边距离相等的点在角的平分线上。
性质和判定的区别和联系:
温馨提醒
性质说明只要是角平分线上的点,它到角两边的距离一定相等,无一例外;判定反映了只要是到角两边距离相等的点,都一定在角的平分线上,而绝不会漏掉一个。
前者用来证明线段相等,后者用来证明角相等(角平分线)
一
填空:
(1).
∵∠1=
∠2,DC⊥AC,
DE⊥AB
∴___________
(___________________________________________)
(2).
∵DC⊥AC
,DE⊥AB
,DC=DE
∴__________
(_____________________________________________)
A
C
D
E
B
1
2
∠1=
∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等
随
练习
堂
图1
图2
B
1:下列两图中,能表示直线l1上一点P到直线l2的距离的是(
)
图1
二
选择题:
2:下列两图中,能表示角的平分线上的一点P到角的边上的距离的是(
)
图1
图1
图2
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
角的平分线上的点到角的两边的距离相等。
BD
CD
三
判断:
(×)
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
角的平分线上的点到角的两边的距离相等。
BD
CD
(×)
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
角的平分线上的点到角的两边的距离相等。
√
情境引入
天泉农副产品集散基地M位于李庄A、王庄B、赵庄C三个村庄之间,其位置到三条公路AB、AC、BC的距离相等。你能在图中
内部画出M的位置吗?
A
C
B
怎样作一个角的平分线?(不用量角器)
A
B
C
P
探究新知
E
A
F
P
E
F
观察领悟作法,探索思考证明方法
已知:
∠BAC(如图)
求作:
∠BAC的角平分线OP
在△AEP和△AFP中
AE=AF
PE=PF
AP=AP
∵△AEP≌△AFP(SSS)
∴∠EAP=∠FAP
即:AP
是∠BAC的角平分线.
1、以A为圆心,适当长为半径作弧,交AB于E,交AC于F。
2、分别以E、F为圆心,大于
的长为半径作弧,两弧在∠BAC内部交于点P。
3、作射线AP,射线OP即为所求。
作法:
B
C
A
P
F
E
证明:连结PE,PC由作法知:
问题1.在上面作法的第二步中,去掉“大于
EF的长”这个条件行吗?
【答案】不行.因为去掉“大于
EF的长”这个条件,所作的两弧可能没有交点,所以就找不到角的平分线.
【答案】若分别以E、F为圆心,大于
EF的长为半径画两弧,两弧的交点可能在∠BAC的内部,也可能在∠BAC的外部,而我们要找的是∠BAC内部的交点,否则两弧交点与顶点连线得到的射线就不是∠BAC的平分线了.
问题2.第二步中所作的两弧交点一定在∠AOB的内部吗?
思考:
要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺
1:20
000)
s
O
公路
铁路
解:
作夹角的角平分线OC,截取
OD=2.5cm
,D即为所求。
D
C
s
O
公路
铁路
3,在Rt三角形ACB中,AD平分
∠BAC
交BC于D,若BC=9,BD=6,求点D到AB边的距离
A
B
D
C
4、ΔABC的角平分线BM,CN相交于点P.
求证:点P到三边AB,BC,CA的距离相等。
A
C
B
M
N
P
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
