北师大版八年级下册数学 1.1 等腰三角形课件 (共20张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 1.1 等腰三角形课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 15:06:33 | ||
图片预览







文档简介
等
腰
三
角
形
学
数
二
初
课件
知识点
典型例题
堂上练习
知识点回顾
出门测
05
04
03
02
01
录
目
知识点
1
等腰三角形
作一条直线L,在L上取点A?,在L外取点B.作出点B关于直线L的对称点C,连结AB、BC.?CA,则可得到一个等腰三角形。
等腰三角形的定义
有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.同学们在自己作出的等腰三角形中,?注明它的腰、底边、顶角和底角。
1
4
2
3
等腰三角形的两底角有什么关系?
顶角的平分线所在的直线是等腰三角形的对称轴吗?
底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在的直线呢?
思考
等腰三角形
等腰三角形是轴对称图形吗?请找出它的对称轴
1
4
2
3
等腰三角形的两底角有什么关系?
顶角的平分线所在的直线是等腰三角形的对称轴吗?
底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在的直线呢?
思考
等腰三角形
等腰三角形是轴对称图形吗?请找出它的对称轴
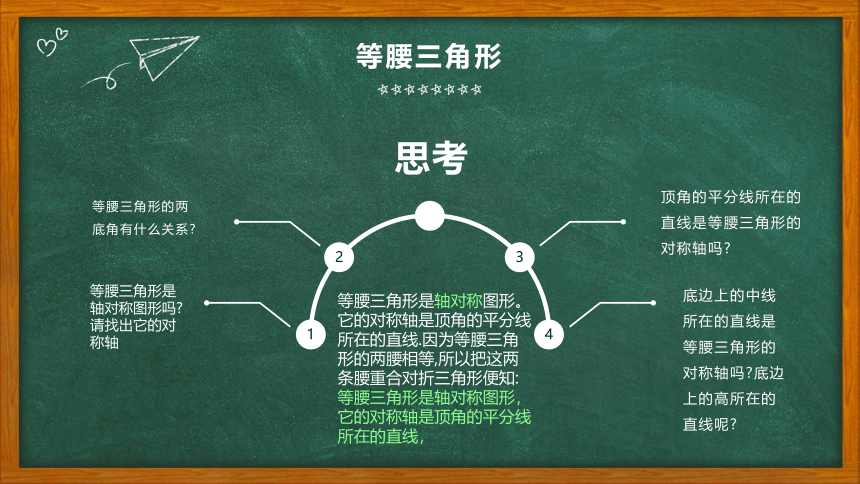
等腰三角形是轴对称图形。它的对称轴是顶角的平分线所在的直线.因为等腰三角形的两腰相等,所以把这两条腰重合对折三角形便知:等腰三角形是轴对称图形,它的对称轴是顶角的平分线所在的直线,
1.等腰三角形的两个底角相等(简写成“等边对等角”)?.
2.等腰三角形的顶角平分线,底边上的中线、?底边上的高互相重合(通常称作“三线合-一”).
等腰三角形
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
等腰三角形
1.等腰三角形的一个角是80°,则它顶角
的度数是( )
A. 80° B. 80°或20°
C
. 80°或50° D. 20°
B
等腰三角形
2.如图,在△ABC中,AB=AC,∠A=40°,
BD为∠ABC的平分线,则∠BDC的度数是( )
A. 60° B. 70°
C. 75° D. 80°
C
等腰三角形
3.已知等腰三角形的两边长分别是3和5,则该三角形的周长是( )
A. 8 B. 9
C. 10或12 D. 11或13
D
典型例题
2
等腰三角形
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
F
E
D
C
B
A
定理 两角及其中一角的对边对应相等的两个三角形全等.(AAS)
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),
∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知)
∴∠C=∠F(等量代换)
∵BC=EF(已知)
∴△ABC≌△DEF(ASA)
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:取BC的中点D, 连接AD.
在△ABD和△ACD中
∵ AB=AC, BD=CD, AD=AD
∴ △ABD≌△ACD (SSS)
∴ ∠B=∠C (全等三角形的对应角相等)
D
证法一:
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:作△ABC顶角∠A的角平分线AD.
在△ABD和△ACD中
∵ AB=AC, ∠BAD=∠CAD, AD=AD
∴ △ABD≌△ACD (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)
D
证法二:
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:在△ABC和△ACB中
∵ AB=AC, ∠A=∠A, AC=AB,
∴ △ABC≌△ACB (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)
证法三:
回顾
4
1.等腰三角形的两个底角相等(简写成“等边对等角”)?.
2.等腰三角形的顶角平分线,底边上的中线、?底边上的高互相重合(通常称作“三线合-一”).
等腰三角形
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
等
腰
三
角
形
谢
谢
课件
1.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A. 40° B. 36° C. 30° D. 25°
走进中考
2.如图,已知△ABC 中,AB=AC,BD、CE是高,BD与CE相交于点O(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)求∠BAD的度数.
达标检测
腰
三
角
形
学
数
二
初
课件
知识点
典型例题
堂上练习
知识点回顾
出门测
05
04
03
02
01
录
目
知识点
1
等腰三角形
作一条直线L,在L上取点A?,在L外取点B.作出点B关于直线L的对称点C,连结AB、BC.?CA,则可得到一个等腰三角形。
等腰三角形的定义
有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.同学们在自己作出的等腰三角形中,?注明它的腰、底边、顶角和底角。
1
4
2
3
等腰三角形的两底角有什么关系?
顶角的平分线所在的直线是等腰三角形的对称轴吗?
底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在的直线呢?
思考
等腰三角形
等腰三角形是轴对称图形吗?请找出它的对称轴
1
4
2
3
等腰三角形的两底角有什么关系?
顶角的平分线所在的直线是等腰三角形的对称轴吗?
底边上的中线所在的直线是等腰三角形的对称轴吗?底边上的高所在的直线呢?
思考
等腰三角形
等腰三角形是轴对称图形吗?请找出它的对称轴
等腰三角形是轴对称图形。它的对称轴是顶角的平分线所在的直线.因为等腰三角形的两腰相等,所以把这两条腰重合对折三角形便知:等腰三角形是轴对称图形,它的对称轴是顶角的平分线所在的直线,
1.等腰三角形的两个底角相等(简写成“等边对等角”)?.
2.等腰三角形的顶角平分线,底边上的中线、?底边上的高互相重合(通常称作“三线合-一”).
等腰三角形
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
等腰三角形
1.等腰三角形的一个角是80°,则它顶角
的度数是( )
A. 80° B. 80°或20°
C
. 80°或50° D. 20°
B
等腰三角形
2.如图,在△ABC中,AB=AC,∠A=40°,
BD为∠ABC的平分线,则∠BDC的度数是( )
A. 60° B. 70°
C. 75° D. 80°
C
等腰三角形
3.已知等腰三角形的两边长分别是3和5,则该三角形的周长是( )
A. 8 B. 9
C. 10或12 D. 11或13
D
典型例题
2
等腰三角形
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
F
E
D
C
B
A
定理 两角及其中一角的对边对应相等的两个三角形全等.(AAS)
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),
∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知)
∴∠C=∠F(等量代换)
∵BC=EF(已知)
∴△ABC≌△DEF(ASA)
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:取BC的中点D, 连接AD.
在△ABD和△ACD中
∵ AB=AC, BD=CD, AD=AD
∴ △ABD≌△ACD (SSS)
∴ ∠B=∠C (全等三角形的对应角相等)
D
证法一:
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:作△ABC顶角∠A的角平分线AD.
在△ABD和△ACD中
∵ AB=AC, ∠BAD=∠CAD, AD=AD
∴ △ABD≌△ACD (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)
D
证法二:
等腰三角形性质 一题多解
定理: 等腰三角形的两个底角相等. (等边对等角)
已知:如图, 在△ABC中, AB=AC.
求证:∠B=∠C.
C
B
A
证明:在△ABC和△ACB中
∵ AB=AC, ∠A=∠A, AC=AB,
∴ △ABC≌△ACB (SAS)
∴ ∠B=∠C (全等三角形的对应角相等)
证法三:
回顾
4
1.等腰三角形的两个底角相等(简写成“等边对等角”)?.
2.等腰三角形的顶角平分线,底边上的中线、?底边上的高互相重合(通常称作“三线合-一”).
等腰三角形
→
→
D
C
B
A
D
C
B
A
D
(C)
B
A
等
腰
三
角
形
谢
谢
课件
1.如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
A. 40° B. 36° C. 30° D. 25°
走进中考
2.如图,已知△ABC 中,AB=AC,BD、CE是高,BD与CE相交于点O(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)求∠BAD的度数.
达标检测
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
