北师大版九年级数学下 册2.1.1: 二次函数 教学课件(共20张PPT)
文档属性
| 名称 | 北师大版九年级数学下 册2.1.1: 二次函数 教学课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 15:04:24 | ||
图片预览








文档简介
第二章 二次函数
第 二章 二次函数
1 二次函数
学 习 目 标
3
1
2
理解二次函数的概念,掌握其一般形式.(重点)
从实际问题出发列二次函数解析式,体验用函数思想去描述、研究变量之间变化规律的意义.(重、难点)
会解决跟二次函数的概念有关的问题.
2.一元二次方程的一般形式是什么?
3.它的解由什么决定的?
1.什么是一元二次方程?定义中注意点是什么?
ax2+bx+c=0(a,b,c为常数,a≠0)
只含有一个未知数
方程是整式方程
未知数的最高次数为2(化简后)
4. 条件a≠0
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a、b、c为常数,a≠0)的形式,这样的方程叫做一元二次方程。
温故知新
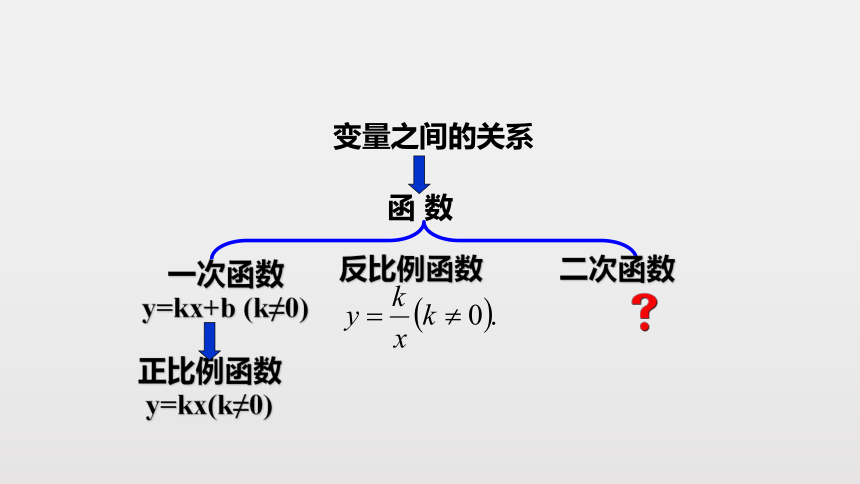
函 数
变量之间的关系
一次函数y=kx+b (k≠0)
反比例函数
二次函数
正比例函数y=kx(k≠0)
4. 函数的定义
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
6.一元二次方程的一般形式
一般地,形如????=????????+????(????,????是常数,????≠????)的函数叫做一次函数.当????=?????时,一次函数????=????????就叫做正比例函数.
?
5. 一次函数与正比例函数
????????????+????????+????=????(????≠????).
?
篮球入框,公园里的喷泉,雨后的彩虹都会形成一条曲线.这些曲线能否用函数关系式表示?
新课导入
你观察过公园的拱桥吗?
源于生活的数学
某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
知识讲解
1.二次函数的定义
问题背景:某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
2)假设果园增种x棵橙子树,那么果园共有_______ 棵橙子树,这时平均每棵树结___________个橙子
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式:
变量:橙子树的数量,橙子树之间的距离,橙子树接受阳光的多少,每棵橙子树的结果量,果园橙子的总产量,每个橙子的质量等等。
y与x的关系式为:
化简为:
(100+x)
(600-5 x)
银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.
?
设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).
y=100x?+200x+100
解:依题意得,
一年后的本息和为:
两年后本息和为 :
所以,y 与x的关系式为:
化简为:
二次函数
y=-5x?+100x+60000
y=100x?+200x+100
思索归纳
有何特点
y是x的函数吗?y是x的一次函数吗?
y是x的反比例函数吗?
二次函数解析式特征
一般地,形如
的函数,叫做二次函数.其中,x是自量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
(1)等号左边是函数y,右边是关于自变量x的
(3)等式右边的最高次数为 ,可以没有一次项和常数项,但 .
注意:
(2) a,b,c为常数,且
(4) 自变量x的取值范围是
整式
a≠0.
2
任意实数
y=ax2+bx+c(a、b、c为常数,a≠0)
不能没有二次项
提醒:当自变量表示实际意义时,自变量的取值范围 就不一定是全体实数。
下列函数中,是二次函数的有哪些?
① y=ax2+bx+c ② ????=????????(x-3)????? ③y=x2
④ ????=???????????? ⑤y=x?+x?+25 ⑥ y=(2x+3)??4x?
?
不一定是,缺少a≠0的条件
不是,等号右边是分式
不是,x的最高次数是3
y=12x+9
2.二次函数的应用
例1
不是,化简后为一次函数
判断一个函数是不是二次函数,要抓住二次函数的结构特征:(1)解析式是关于自变量的整式;(2)自变量的最高次数是2;(3)化简后二次项系数不为0.
除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式,如 ????=????????????,????=????????????+????????,?????=????????????+????等.
?
解题小结
(1)m取什么值时,此函数是一次函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由一次函数的定义可知,
解得????=±22.
?
解得m=3.
注意:第(2)问中不要忽略二次项系数a≠0这一限制条件,从而得出????=????或?????的错误答案.
?
(2)由二次函数的定义可知,
例2
本题考查一次函数和二次函数的概念,这类题要紧扣概念进行解题.此外在求解有关二次函数定义的问题时要确保二次项系数不为0,此题即????+3≠0.
?
解题小结
想一想
二次函数的一般式????=????????????+????????+????(????≠????)与前面我们学过的一元二次方程????????????+????????+????=????(????≠????)有什么联系和区别?
?
联系:(1)等式一边都是????????????+????????+????且????≠????;
(2)方程????????????+????????+????=????可以看成是函数????=?????????????+????????+????中????=????时得到的.
?
区别:前者是函数,后者是方程;等式另一边前者是????,后者是0.
?
随堂训练
2.函数 ????=(?????????)????????+?????????+?????是二次函数的条件是( )
A . ????,????是常数,且????≠???? B . ????,????是常数,且????≠????
C. ????,????是常数,且????≠???? D .?????,????为任何实数
?
C
3.二次函数????=????(????+????)?????3的二次项是____,一次项系数是_____,
常数项是 .
?
1.下列函数中,????是????的二次函数的是 ( )
A.y=2x+1 B.????????+?????????=????
C.????????=3x+1 D.????=????????+????????
?
B
????????????
?
????
?
????
?
4.矩形的周长为16 cm,它的一边长为x(cm),面积为y(cm2).
(1)求y与x之间的函数解析式及自变量x的取值范围;
(2)求当x=3时矩形的面积.
解:(1)????=(????-????)????=-????????+??????????(????<????<????).
(2)当????=????时,????=-????????+????×????=????????(??????????????).
?
课堂小结
二次函数
定 义
????=????????????+????????+????(?????≠????,????,????,????是常数)
?
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
????=????????????;
????=????????????+????????;
????=????????????+????(?????≠????,????,????,????是常数).
?
再见
第 二章 二次函数
1 二次函数
学 习 目 标
3
1
2
理解二次函数的概念,掌握其一般形式.(重点)
从实际问题出发列二次函数解析式,体验用函数思想去描述、研究变量之间变化规律的意义.(重、难点)
会解决跟二次函数的概念有关的问题.
2.一元二次方程的一般形式是什么?
3.它的解由什么决定的?
1.什么是一元二次方程?定义中注意点是什么?
ax2+bx+c=0(a,b,c为常数,a≠0)
只含有一个未知数
方程是整式方程
未知数的最高次数为2(化简后)
4. 条件a≠0
只含有一个未知数x的整式方程,并且都可以化为ax2+bx+c=0(a、b、c为常数,a≠0)的形式,这样的方程叫做一元二次方程。
温故知新
函 数
变量之间的关系
一次函数y=kx+b (k≠0)
反比例函数
二次函数
正比例函数y=kx(k≠0)
4. 函数的定义
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
6.一元二次方程的一般形式
一般地,形如????=????????+????(????,????是常数,????≠????)的函数叫做一次函数.当????=?????时,一次函数????=????????就叫做正比例函数.
?
5. 一次函数与正比例函数
????????????+????????+????=????(????≠????).
?
篮球入框,公园里的喷泉,雨后的彩虹都会形成一条曲线.这些曲线能否用函数关系式表示?
新课导入
你观察过公园的拱桥吗?
源于生活的数学
某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有哪些变量?其中哪些是自变量?哪些是因变量?
(2)假设果园增种x棵橙子树,那么果园共有多少棵橙子树?这时平均每棵树结多少个橙子?
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式.
知识讲解
1.二次函数的定义
问题背景:某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)问题中有那些变量?其中哪些是自变量?哪些是因变量?
2)假设果园增种x棵橙子树,那么果园共有_______ 棵橙子树,这时平均每棵树结___________个橙子
(3)如果果园橙子的总产量为y个,那么请你写出y与x之间的关系式:
变量:橙子树的数量,橙子树之间的距离,橙子树接受阳光的多少,每棵橙子树的结果量,果园橙子的总产量,每个橙子的质量等等。
y与x的关系式为:
化简为:
(100+x)
(600-5 x)
银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是由中国人民银行根据国民经济发展的情况而决定的.
?
设人民币一年定期储蓄的年利率是x,一年到期后,银行将本金和利息自动按一年定期储蓄转存.如果存款是100元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).
y=100x?+200x+100
解:依题意得,
一年后的本息和为:
两年后本息和为 :
所以,y 与x的关系式为:
化简为:
二次函数
y=-5x?+100x+60000
y=100x?+200x+100
思索归纳
有何特点
y是x的函数吗?y是x的一次函数吗?
y是x的反比例函数吗?
二次函数解析式特征
一般地,形如
的函数,叫做二次函数.其中,x是自量,a,b,c分别是函数表达式的二次项系数、一次项系数和常数项.
(1)等号左边是函数y,右边是关于自变量x的
(3)等式右边的最高次数为 ,可以没有一次项和常数项,但 .
注意:
(2) a,b,c为常数,且
(4) 自变量x的取值范围是
整式
a≠0.
2
任意实数
y=ax2+bx+c(a、b、c为常数,a≠0)
不能没有二次项
提醒:当自变量表示实际意义时,自变量的取值范围 就不一定是全体实数。
下列函数中,是二次函数的有哪些?
① y=ax2+bx+c ② ????=????????(x-3)????? ③y=x2
④ ????=???????????? ⑤y=x?+x?+25 ⑥ y=(2x+3)??4x?
?
不一定是,缺少a≠0的条件
不是,等号右边是分式
不是,x的最高次数是3
y=12x+9
2.二次函数的应用
例1
不是,化简后为一次函数
判断一个函数是不是二次函数,要抓住二次函数的结构特征:(1)解析式是关于自变量的整式;(2)自变量的最高次数是2;(3)化简后二次项系数不为0.
除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式,如 ????=????????????,????=????????????+????????,?????=????????????+????等.
?
解题小结
(1)m取什么值时,此函数是一次函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由一次函数的定义可知,
解得????=±22.
?
解得m=3.
注意:第(2)问中不要忽略二次项系数a≠0这一限制条件,从而得出????=????或?????的错误答案.
?
(2)由二次函数的定义可知,
例2
本题考查一次函数和二次函数的概念,这类题要紧扣概念进行解题.此外在求解有关二次函数定义的问题时要确保二次项系数不为0,此题即????+3≠0.
?
解题小结
想一想
二次函数的一般式????=????????????+????????+????(????≠????)与前面我们学过的一元二次方程????????????+????????+????=????(????≠????)有什么联系和区别?
?
联系:(1)等式一边都是????????????+????????+????且????≠????;
(2)方程????????????+????????+????=????可以看成是函数????=?????????????+????????+????中????=????时得到的.
?
区别:前者是函数,后者是方程;等式另一边前者是????,后者是0.
?
随堂训练
2.函数 ????=(?????????)????????+?????????+?????是二次函数的条件是( )
A . ????,????是常数,且????≠???? B . ????,????是常数,且????≠????
C. ????,????是常数,且????≠???? D .?????,????为任何实数
?
C
3.二次函数????=????(????+????)?????3的二次项是____,一次项系数是_____,
常数项是 .
?
1.下列函数中,????是????的二次函数的是 ( )
A.y=2x+1 B.????????+?????????=????
C.????????=3x+1 D.????=????????+????????
?
B
????????????
?
????
?
????
?
4.矩形的周长为16 cm,它的一边长为x(cm),面积为y(cm2).
(1)求y与x之间的函数解析式及自变量x的取值范围;
(2)求当x=3时矩形的面积.
解:(1)????=(????-????)????=-????????+??????????(????<????<????).
(2)当????=????时,????=-????????+????×????=????????(??????????????).
?
课堂小结
二次函数
定 义
????=????????????+????????+????(?????≠????,????,????,????是常数)
?
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
????=????????????;
????=????????????+????????;
????=????????????+????(?????≠????,????,????,????是常数).
?
再见
