北师大版七年级数学上册课件:第三章《整式及其加减》回顾与思考(共22张PPT)
文档属性
| 名称 | 北师大版七年级数学上册课件:第三章《整式及其加减》回顾与思考(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 17:15:55 | ||
图片预览







文档简介
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
北师大数学七年级上册
§3.6 整式及其加减
——回顾与思考
第三章 整式及其运算
梳理所学知识,形成一定的体系, 并逐步掌握用代数式表达数量关系或变化规律的方法;能解释一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系;经历探索事物之间的数量关系,并用字母与代数式表示,建立初步符号感, 发展抽象思维.
复习目标
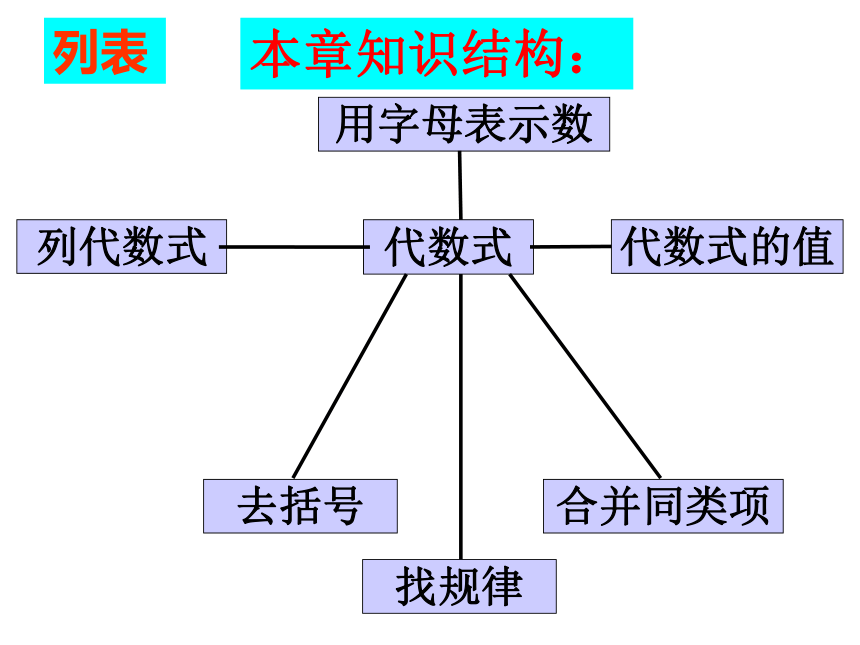
用字母表示数
代数式
列代数式
去括号
合并同类项
找规律
代数式的值
本章知识结构:
列表
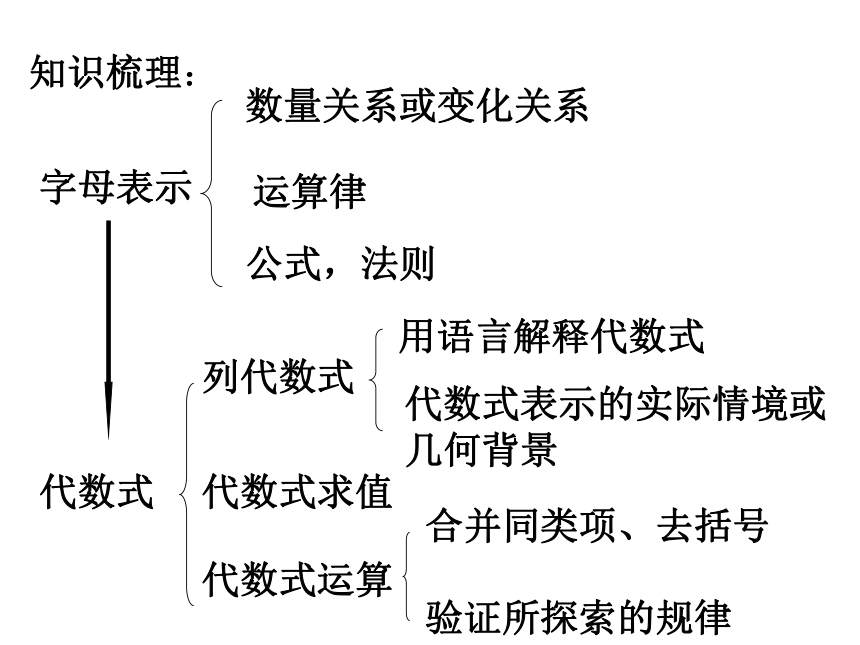
知识梳理:
字母表示
数量关系或变化关系
运算律
公式,法则
代数式
列代数式
代数式求值
代数式运算
合并同类项、去括号
验证所探索的规律
用语言解释代数式
代数式表示的实际情境或几何背景
代数式是用基本运算符号把数字、表示数的字母连接起的式子。
注意:
1.单独一个数或一个字母也是代数式.
2.式子不含“=”、“>”、“<”、“≤”、“≥”
(运算符号包括加、减、乘、除、乘方)
像4+3(x-1), x+x+(x+1), a+b, ab, 2(m+n), a3等式子都是代数式。
(3) 数字通常写在字母前面;
(1) a×b通常写作a·b或ab;
(2) 1÷a 通常写作 ;
如: a×3通常写作3a
(4)带分数一般写成假分数.
如: ×a 通常写作 a
代数式的规范写法:
分清哪些是同类项是合并同类项的关键.
合并同类项时注意:
1、同类项合并过程中,把同类项的系数相加,字母和字母的指数不变。不是同类项不可以合并。
2、在求代数式的值时,可先合并同类项将代数式化简,然后再代入数值计算,这样往往会简化运算过程。
(1)所含字母相同,
(2)相同字母的指数也相同。
括号前是“+”号,把括号和它前面的“+”号去掉后,原来括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原来括号里各项的符号都要改变.
去括号法则:
1、某产品的成本由x元下降10%后是 __________元.
2、 十位上的数字是m,个位上的数字比十位上的数字大4的两位数是__________.
变式:a是一个两位数,b是一个一位数(不为0),若把b放在a的左边组成一个三位数,这个三位数是___________.
(1-10%) x
10m+m+4
100b+a
习题讲解
3、求代数式b2 -4ac的值,其中a=-1, b=-3, c=2。
4、若3xmy3与- xyn是同类项,则m= , n= .
5、计算:
① 2a+(x+y) -2(a-b )
② a-[b-(c-b)]
17
1
3
2b+x+y
a-2b+c
6、如图所示的计算程序,若开始输入的x的值为5,则最后输出的结果是_________
输入x
-3
÷4
输出
输入x
输出
4x+7
0.5
×4
+7
7、先化简,再求值:
6xy –[3x2-2(x2-2xy)+1], 其中
x=-1, y=2.
-x2+2xy-1 , -6
9、4
8、
8、设a-b=2,a-c= , 求
(a-b)2+3(b-c)+ 的值.
9、如果a2-a-1=2,求a-a2+1的值.
1.举例说明下列各代数式的意义.
(1) a2-b2_____. (2) (1-20%)x_____.
解: (1) a2-b2表示为a、b两数的平方差;或表示为正方形边长为a与边长为b的面积之差.
(2) (1-20%)x表示为: 一台洗衣机原价为x元, 降价20%后的售价, 也可表示: 比x少20%的数.
典型习题
2.化简下列各式
(1) 2(2a2+9b)+3(-5a2-4b)
(2) -3(2x2-xy)+4(x2+xy-6)
解:(1) 2(2a2+9b)+3(-5a2-4b)
=4a2+18b-15a2-12b= -11a2+6b
(2) -3(2x2-xy)+4(x2+xy-6)
= -6x2+3xy+4x2+4xy-24
= -2x2+7xy-24
3. 先化简,再求值.
2(a2b+ab2)-2(a2b-1)-2ab2-2, 其中a=-2,b=2.
解:2(a2b+ab2)-2(a2b-1)-2ab2-2
=2a2b+2ab2-2a2b+2-2ab2-2=0
当a=-2,b=2时,原式=0.
1.把x本书分给若干学生,若每人分12本书,尚余5本,用代数式表示学生总数_________.
2.将1000元钱按定期储蓄存入银行,月利率0. 98%,一年后的利息是____________.
3.代数式-ab2c3的系数是_____.
117.6元
-1
达标检测
4. 观察下列各数,按规律在横线上填上适当的数.
(1)1,1,2,3,5,_____,13,21,34,_____,_____.
(2)1,-2,4,-8,16,_____,_____.
5. 已知a=11,b= ,则代数式:a+2a+3a+…+9a+10a+10b+9b+…+3b+2b+b的值是_____.
8
55
89
-32
64
610
6. 合并同类项:
(1)5xy2-8xy2+2xy2
(2)6(a+b) +4(a+b) -5(a+b)
(1) -xy2 (2) 5(a+b)
归纳总结
1. 先化简,再求值
5abc-{2a2b-[3abc-(4ab2-a2b)]},其中a=-2, b=-1, c=3.
8abc-a2b-4ab2 60
强化训练
(7) 若 ,则 _______
(1)若x+1=4, 则 ___________
(2) 若x+1=5,则 _______
(3) 若x+5y=4,则2x+10y=_______
(4) 若x+5y=4,则2x+7+10y=_____
(5) 若 ,则 _______
(6) 若 ,则x=__________
2.你来试一试!
16
24
8
15
8
强化训练
单击此处编辑母版副标题样式
*
*
*
北师大数学七年级上册
§3.6 整式及其加减
——回顾与思考
第三章 整式及其运算
梳理所学知识,形成一定的体系, 并逐步掌握用代数式表达数量关系或变化规律的方法;能解释一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系;经历探索事物之间的数量关系,并用字母与代数式表示,建立初步符号感, 发展抽象思维.
复习目标
用字母表示数
代数式
列代数式
去括号
合并同类项
找规律
代数式的值
本章知识结构:
列表
知识梳理:
字母表示
数量关系或变化关系
运算律
公式,法则
代数式
列代数式
代数式求值
代数式运算
合并同类项、去括号
验证所探索的规律
用语言解释代数式
代数式表示的实际情境或几何背景
代数式是用基本运算符号把数字、表示数的字母连接起的式子。
注意:
1.单独一个数或一个字母也是代数式.
2.式子不含“=”、“>”、“<”、“≤”、“≥”
(运算符号包括加、减、乘、除、乘方)
像4+3(x-1), x+x+(x+1), a+b, ab, 2(m+n), a3等式子都是代数式。
(3) 数字通常写在字母前面;
(1) a×b通常写作a·b或ab;
(2) 1÷a 通常写作 ;
如: a×3通常写作3a
(4)带分数一般写成假分数.
如: ×a 通常写作 a
代数式的规范写法:
分清哪些是同类项是合并同类项的关键.
合并同类项时注意:
1、同类项合并过程中,把同类项的系数相加,字母和字母的指数不变。不是同类项不可以合并。
2、在求代数式的值时,可先合并同类项将代数式化简,然后再代入数值计算,这样往往会简化运算过程。
(1)所含字母相同,
(2)相同字母的指数也相同。
括号前是“+”号,把括号和它前面的“+”号去掉后,原来括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原来括号里各项的符号都要改变.
去括号法则:
1、某产品的成本由x元下降10%后是 __________元.
2、 十位上的数字是m,个位上的数字比十位上的数字大4的两位数是__________.
变式:a是一个两位数,b是一个一位数(不为0),若把b放在a的左边组成一个三位数,这个三位数是___________.
(1-10%) x
10m+m+4
100b+a
习题讲解
3、求代数式b2 -4ac的值,其中a=-1, b=-3, c=2。
4、若3xmy3与- xyn是同类项,则m= , n= .
5、计算:
① 2a+(x+y) -2(a-b )
② a-[b-(c-b)]
17
1
3
2b+x+y
a-2b+c
6、如图所示的计算程序,若开始输入的x的值为5,则最后输出的结果是_________
输入x
-3
÷4
输出
输入x
输出
4x+7
0.5
×4
+7
7、先化简,再求值:
6xy –[3x2-2(x2-2xy)+1], 其中
x=-1, y=2.
-x2+2xy-1 , -6
9、4
8、
8、设a-b=2,a-c= , 求
(a-b)2+3(b-c)+ 的值.
9、如果a2-a-1=2,求a-a2+1的值.
1.举例说明下列各代数式的意义.
(1) a2-b2_____. (2) (1-20%)x_____.
解: (1) a2-b2表示为a、b两数的平方差;或表示为正方形边长为a与边长为b的面积之差.
(2) (1-20%)x表示为: 一台洗衣机原价为x元, 降价20%后的售价, 也可表示: 比x少20%的数.
典型习题
2.化简下列各式
(1) 2(2a2+9b)+3(-5a2-4b)
(2) -3(2x2-xy)+4(x2+xy-6)
解:(1) 2(2a2+9b)+3(-5a2-4b)
=4a2+18b-15a2-12b= -11a2+6b
(2) -3(2x2-xy)+4(x2+xy-6)
= -6x2+3xy+4x2+4xy-24
= -2x2+7xy-24
3. 先化简,再求值.
2(a2b+ab2)-2(a2b-1)-2ab2-2, 其中a=-2,b=2.
解:2(a2b+ab2)-2(a2b-1)-2ab2-2
=2a2b+2ab2-2a2b+2-2ab2-2=0
当a=-2,b=2时,原式=0.
1.把x本书分给若干学生,若每人分12本书,尚余5本,用代数式表示学生总数_________.
2.将1000元钱按定期储蓄存入银行,月利率0. 98%,一年后的利息是____________.
3.代数式-ab2c3的系数是_____.
117.6元
-1
达标检测
4. 观察下列各数,按规律在横线上填上适当的数.
(1)1,1,2,3,5,_____,13,21,34,_____,_____.
(2)1,-2,4,-8,16,_____,_____.
5. 已知a=11,b= ,则代数式:a+2a+3a+…+9a+10a+10b+9b+…+3b+2b+b的值是_____.
8
55
89
-32
64
610
6. 合并同类项:
(1)5xy2-8xy2+2xy2
(2)6(a+b) +4(a+b) -5(a+b)
(1) -xy2 (2) 5(a+b)
归纳总结
1. 先化简,再求值
5abc-{2a2b-[3abc-(4ab2-a2b)]},其中a=-2, b=-1, c=3.
8abc-a2b-4ab2 60
强化训练
(7) 若 ,则 _______
(1)若x+1=4, 则 ___________
(2) 若x+1=5,则 _______
(3) 若x+5y=4,则2x+10y=_______
(4) 若x+5y=4,则2x+7+10y=_____
(5) 若 ,则 _______
(6) 若 ,则x=__________
2.你来试一试!
16
24
8
15
8
强化训练
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
