北师大版数学九年级下册:3.9弧长及扇形的面积 课件(17张PPT)
文档属性
| 名称 | 北师大版数学九年级下册:3.9弧长及扇形的面积 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览






文档简介
第 三章 圆
3.9 弧长及扇形的面积
第三章 圆
学习目标
1.理解弧长和扇形面积公式的探求过程.(难点)
2.会利用弧长和扇形面积的计算公式进行计算.(重点)
1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?
2.什么叫圆心角?
C=2πR,S=πR2.
角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角.
新课导入
一、弧长公式
知识讲解
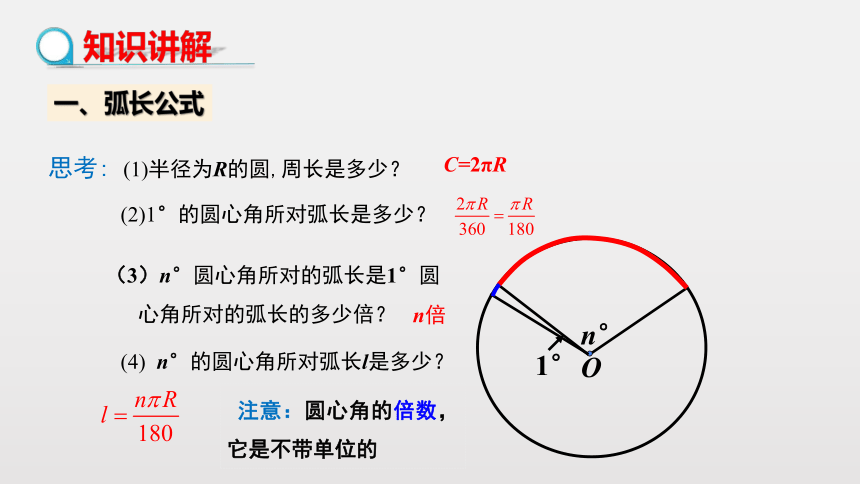
思考: (1)半径为R的圆,周长是多少?
(2)1°的圆心角所对弧长是多少?
n°
O
(4) n°的圆心角所对弧长l是多少?
1°
C=2πR
(3)n°圆心角所对的弧长是1°圆
心角所对的弧长的多少倍?
n倍
注意:圆心角的倍数,它是不带单位的
例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).
解:R=40mm, n=110,
∴ AB的长=
︵
≈76.8(mm)
因此,管道的展直长度约为76.8mm.
例题讲解
1.若圆的半径为R,60°的圆心角所对的弧长为l,则( )
A. l=R B. l2.在半径为12cm的圆中,150°的圆心角所对的弧长等
于( )
A.24πcm B.12πcm
C.10πcm D.5πcm
C
C
跟踪训练
3.如图,⊙O及两个半径为1的⊙O1和⊙O2两两外切,切点
分别为 A,B,C,且∠O=90°,则 的长为
( )
A. B. C. D.2π
O
C
B
A
O2
O1
B
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
探究
二、扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为S扇形= .
比较扇形面积公式与弧长公式,你能用弧长来表示扇形的面积吗?
S扇形= l ,
例2.扇形AOB的半径为12cm,∠AOB= 120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2).
解:
AB的长=
︵
≈25.1(cm).
S扇形=
≈150.8(cm2).
因此,AB的长约为25.1cm,扇形AOB的面积约为150.8cm2.
︵
例题讲解
1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长
是( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
跟踪训练
4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿
路线爬行,乙虫沿 路线爬行,则下列结
论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
A
C
G
F
E
B
A3
A2
A1
D
答案:C
当堂检测
1.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( )
A. 233???? B. 13???? C. 23???? D. 33?????
?
2.如图,分别以n边形的顶点为圆心,以1cm为半径画圆,当n=2019时,则图中阴影部分的面积之和为( )
A.2πcm2 B.πcm2
C.2018πcm2 D.2019πcm2
C
B
3.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 BC 的长为 .
4.如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
(
????????????
?
6π
5.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4m长的绳子一端拴在墙角O处(OA>4m,OB>4m),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π).
解:(1)小狗可活动的最大区域图形的周长为: 150????×4180 = 103???? (m);
(2)小狗可活动的最大区域图形的面积为: 150×42????360 = 203???? (m2).
?
0
0
课堂小结
弧长
计算公式:????=????????????180
?
扇形
定义
公式
阴影部分面积
求法:整体思想
再见
3.9 弧长及扇形的面积
第三章 圆
学习目标
1.理解弧长和扇形面积公式的探求过程.(难点)
2.会利用弧长和扇形面积的计算公式进行计算.(重点)
1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?
2.什么叫圆心角?
C=2πR,S=πR2.
角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角.
新课导入
一、弧长公式
知识讲解
思考: (1)半径为R的圆,周长是多少?
(2)1°的圆心角所对弧长是多少?
n°
O
(4) n°的圆心角所对弧长l是多少?
1°
C=2πR
(3)n°圆心角所对的弧长是1°圆
心角所对的弧长的多少倍?
n倍
注意:圆心角的倍数,它是不带单位的
例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).
解:R=40mm, n=110,
∴ AB的长=
︵
≈76.8(mm)
因此,管道的展直长度约为76.8mm.
例题讲解
1.若圆的半径为R,60°的圆心角所对的弧长为l,则( )
A. l=R B. l
于( )
A.24πcm B.12πcm
C.10πcm D.5πcm
C
C
跟踪训练
3.如图,⊙O及两个半径为1的⊙O1和⊙O2两两外切,切点
分别为 A,B,C,且∠O=90°,则 的长为
( )
A. B. C. D.2π
O
C
B
A
O2
O1
B
在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?
探究
二、扇形面积公式
如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为S扇形= .
比较扇形面积公式与弧长公式,你能用弧长来表示扇形的面积吗?
S扇形= l ,
例2.扇形AOB的半径为12cm,∠AOB= 120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2).
解:
AB的长=
︵
≈25.1(cm).
S扇形=
≈150.8(cm2).
因此,AB的长约为25.1cm,扇形AOB的面积约为150.8cm2.
︵
例题讲解
1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长
是( )
A. 3π B.4π C.5π D.6π
π
π
150o
B
跟踪训练
4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿
路线爬行,乙虫沿 路线爬行,则下列结
论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定
A
C
G
F
E
B
A3
A2
A1
D
答案:C
当堂检测
1.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( )
A. 233???? B. 13???? C. 23???? D. 33?????
?
2.如图,分别以n边形的顶点为圆心,以1cm为半径画圆,当n=2019时,则图中阴影部分的面积之和为( )
A.2πcm2 B.πcm2
C.2018πcm2 D.2019πcm2
C
B
3.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则 BC 的长为 .
4.如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .
(
????????????
?
6π
5.如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4m长的绳子一端拴在墙角O处(OA>4m,OB>4m),另一端栓一只小狗,小狗在地面上活动,求
(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π).
解:(1)小狗可活动的最大区域图形的周长为: 150????×4180 = 103???? (m);
(2)小狗可活动的最大区域图形的面积为: 150×42????360 = 203???? (m2).
?
0
0
课堂小结
弧长
计算公式:????=????????????180
?
扇形
定义
公式
阴影部分面积
求法:整体思想
再见
