北师大版九年级下册数学 3.8 圆内接正多边形 同步习题(word版含答案)
文档属性
| 名称 | 北师大版九年级下册数学 3.8 圆内接正多边形 同步习题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 20:11:00 | ||
图片预览




文档简介
3.8
圆内接正多边形
同步习题
一.选择题
1.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A.
B.
C.
D.
2.如图,已知正五边形ABCDE内接于⊙O,连结BD,CE相交于点F,则∠BFC的度数是( )
A.60°
B.70°
C.72°
D.90°
3.如图是半径为2的⊙O的内接正六边形ABCDEF,则圆心O到边AB的距离是( )
A.2
B.1
C.
D.
4.如图,AB,AC分别为⊙O的内接正三角形和内接正四边形的一边,若BC恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8
B.10
C.12
D.15
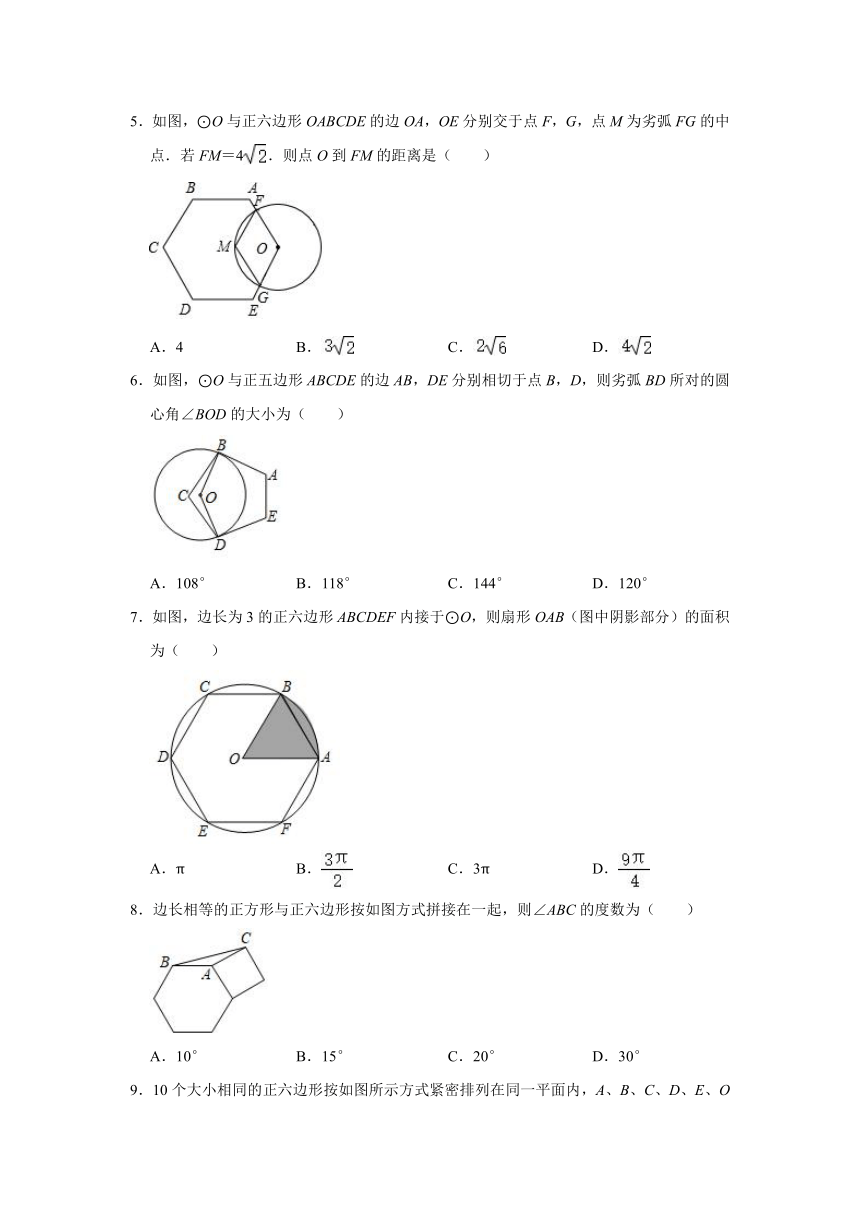
5.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4.则点O到FM的距离是( )
A.4
B.
C.
D.
6.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为( )
A.108°
B.118°
C.144°
D.120°
7.如图,边长为3的正六边形ABCDEF内接于⊙O,则扇形OAB(图中阴影部分)的面积为( )
A.π
B.
C.3π
D.
8.边长相等的正方形与正六边形按如图方式拼接在一起,则∠ABC的度数为( )
A.10°
B.15°
C.20°
D.30°
9.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点.则点O是下列哪个三角形的外心( )
A.△AED
B.△ABD
C.△BCD
D.△ACD
10.如图,以正六边形ABCDEF的对角线CF为边,再作一个正六边形CFGHMN,若AB=,则EG的长为( )
A.2
B.2
C.3
D.2
二.填空题
11.用正五边形钢板制作一个边框总长为40cm的五角星(如图),则正五边形的边长为
cm(保留根号).
12.用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为
cm.
13.同圆的内接正三边形、正四边形、正六边形的边长之比为
.
14.如图,在正九边形ABCDEFGHI中,若AB+AC=3,则对角线AE=
.
15.如图,有一个圆O和两个正六边形T1,T2,T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).若设T1,T2的边长分别为a,b,圆O的半径为r,则r:a=
;r:b=
.
三.解答题
16.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
17.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OA、OD、OE、AE、DE.
(1)求∠AED的度数;
(2)当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
18.如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为
.
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
参考答案
一.选择题
1.解:如图,连接OA、OB,作OG⊥AB于点G,
∵⊙O的周长等于4πcm,
∴⊙O的半径为:=2,
∵ABCDEF是⊙O的内接正六边形,
∴OA=OB=AB=2,
∵OG⊥AB,
∴AG=BG=AB=1,
∴OG=,
∴S△AOB=AB?OG
=2×
=.
∴它的内接正六边形ABCDEF的面积是6S△AOB=6(cm2).
故选:C.
2.解:如图所示:
∵五边形ABCDE为正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,
∴∠CBD=∠CDB=∠CED=∠DCE==36°,
∴∠BFC=∠BDC+∠DCE=72°.
故选:C.
3.解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB==60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选:C.
4.解:连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC==90°,∠AOB==120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n==12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:C.
5.解:连接ON,过O作OH⊥FM于H,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,
∵OH⊥FM,OF=OM,
∴∠OFH=60°,∠OHF=90°,FH=FM=2,
∴OH=FH=2,
故选:C.
6.解:∵五边形ABCDE是正五边形,
∴∠E=∠A=180°﹣=108°.
∵AB、DE与⊙O相切,
∴∠OBA=∠ODE=90°,
∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,
故选:C.
7.解:∵正六边形ABCDEF内接于⊙O,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴扇形AOB的面积==,
故选:B.
8.解:由题意得:正六边形的每个内角都等于120°,正方形的每个内角都等于90°,
故∠BAC=360°﹣120°﹣90°=150°,
∵AB=AC,
∴∠ABC=∠ACB==15°.
故选:B.
9.解:从O点出发,确定点O分别到A,B,C,D,E的距离,只有OA=OC=OD,
∵三角形的外心到三角形的三个顶点的距离相等,
∴点O是△ACD的外心,
故选:D.
10.解:延长DE交AG于T.
由题意FG=2EF,∠EFC=∠EFT=60°,
∵∠DEF=120°,
∴∠EFT=60°,
∴∠EFT=∠FET=∠ETF=60°,
∴EF=FT=ET,
∴TG=TF=ET,
∴∠FEG=90°,
∵AB=AF=EF=,
∴EG=EF?tan60°=3,
故选:C.
二.填空题
11.解:∵五边形ABCDE是正五边形,
∴五边形ABCDE为圆内接正五边形,
∴====,
∴∠BAE==108°,∠HAN=∠AEH=∠BAC=∠DAE=∠ABE=∠BAE=×108°=36°,
∴∠EAH=∠BAN=36°+36°=72°,
∴∠AHE=180°﹣72°﹣36°=72°,∠ANB=180°﹣72°﹣36°=72°,
∴∠EAH=∠EHA=72°,∠ANH=∠AHN=72°,
∴AE=HE,∠EAH=∠EHA=∠ANH=∠AHN,
∴△AEH∽△AHN,
∴=,
∵五角星的边框总长为40cm,
∴AH=AN=EN==4,HN=HE﹣NE=AE﹣4,
∴=,
整理得:(AE﹣2)2=20,
∴AE=2+2(cm),
故答案为:2+2.
12.解:如图所示:
作AM⊥CB于M,则AM=2,
∵六边形ABCDEF是正六边形,
∴∠ABC=120°,
∴∠ABM=180°﹣120°=60°,
∵sin∠ABM=,
∴AB===;
故答案为:.
13.解:设圆的半径为r,
如图①,∠AOB=×360°=120°,
∵OA=OB,
∴∠OAB=30°,
过点O作OC⊥AB于点C,
则AB=2AC,
∵AC=OA?cos30°=r,
∴AB=r;
如图②,∠AOB=×360°=90°,
∵OA=OB,
∴AB=OA=r;
如图③,∠AOB=×360°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴AB=OA=r;
∴同圆的内接正三边形、正四边形、正六边形的边长之比为:::1.
故答案为:::1.
14.解:∵正九边形内角和为(9﹣2)×180°=1260°,
∴每个内角为140°,
又∵AB=BC,∠B=140°,
∴∠CAB=(180°﹣140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°﹣2×20°﹣40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=30°,
∴AC=AH=2AM=2x,
∴AB+AC=y+2x,
∵AE=AM+MN+EN=2x+y,
∴AE=AB+AC=3.
故答案为:3.
15.解:连接OE、OG,OF,
∵EF=a,且正六边形T1,
∴△OEF为等边三角形,OE为圆的半径r,
∴a:r=1:1;
由题意可知OG为∠FOE的平分线,即∠EOG=∠EOF=30°,
在Rt△OEG中,OE=r,OG=b,
∵==cos∠EOG=cos30°,即=,
∵r:a=1:1;r:b=:2;
故答案为:r:a=1:1;r:b=:2;
三.解答题
16.(1)解:∵六边形ABCDEF是正六边形,
∴∠FAB==120°;
(2)证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FAB=∠CBA,
∴∠OAG=∠OBH,
在△AOG和△BOH中,
,
∴△AOG≌△BOH(SAS)
∴OG=OH.
17.解:(1)连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
18.解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
△ABC就是所求的三角形;
(2)在直角△ABD中,AD==,
则BC=AD=,CD=AB=x.
则矩形的周长是:2x+2,
故答案是:2x+2;
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG?AD,
∴DG==,
∴BC=EF=AD﹣2DG=2r﹣.
则L=4x+4r﹣.
当x=﹣=r时,L取得最大值.最大值是:6r.
圆内接正多边形
同步习题
一.选择题
1.如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A.
B.
C.
D.
2.如图,已知正五边形ABCDE内接于⊙O,连结BD,CE相交于点F,则∠BFC的度数是( )
A.60°
B.70°
C.72°
D.90°
3.如图是半径为2的⊙O的内接正六边形ABCDEF,则圆心O到边AB的距离是( )
A.2
B.1
C.
D.
4.如图,AB,AC分别为⊙O的内接正三角形和内接正四边形的一边,若BC恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8
B.10
C.12
D.15
5.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=4.则点O到FM的距离是( )
A.4
B.
C.
D.
6.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为( )
A.108°
B.118°
C.144°
D.120°
7.如图,边长为3的正六边形ABCDEF内接于⊙O,则扇形OAB(图中阴影部分)的面积为( )
A.π
B.
C.3π
D.
8.边长相等的正方形与正六边形按如图方式拼接在一起,则∠ABC的度数为( )
A.10°
B.15°
C.20°
D.30°
9.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A、B、C、D、E、O均是正六边形的顶点.则点O是下列哪个三角形的外心( )
A.△AED
B.△ABD
C.△BCD
D.△ACD
10.如图,以正六边形ABCDEF的对角线CF为边,再作一个正六边形CFGHMN,若AB=,则EG的长为( )
A.2
B.2
C.3
D.2
二.填空题
11.用正五边形钢板制作一个边框总长为40cm的五角星(如图),则正五边形的边长为
cm(保留根号).
12.用两条宽均为2cm的纸条(假设纸条的长度足够长),折叠穿插,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正六边形ABCDEF,则折出的正六边形的边长为
cm.
13.同圆的内接正三边形、正四边形、正六边形的边长之比为
.
14.如图,在正九边形ABCDEFGHI中,若AB+AC=3,则对角线AE=
.
15.如图,有一个圆O和两个正六边形T1,T2,T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).若设T1,T2的边长分别为a,b,圆O的半径为r,则r:a=
;r:b=
.
三.解答题
16.如图,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且AG=BH.
(1)求∠FAB的度数;
(2)求证:OG=OH.
17.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OA、OD、OE、AE、DE.
(1)求∠AED的度数;
(2)当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
18.如图,圆O的半径为r.
(1)在图①中,画出圆O的内接正△ABC,简要写出画法;求出这个正三角形的周长.
(2)在图②中,画出圆O的内接矩形ABCD,简要写出画法;若设AB=x,则矩形的周长为
.
(3)如图③,六边形ABCDEF内接于半径为r(常数)的⊙O,其中AD为直径,且AB=CD=DE=FA.设AB=x,求六边形ABCDEF的周长L关于x的函数关系式,并探究L是否有最大值,若有,请指出x为何值时,L取得最大值;若没有,请说明理由.
参考答案
一.选择题
1.解:如图,连接OA、OB,作OG⊥AB于点G,
∵⊙O的周长等于4πcm,
∴⊙O的半径为:=2,
∵ABCDEF是⊙O的内接正六边形,
∴OA=OB=AB=2,
∵OG⊥AB,
∴AG=BG=AB=1,
∴OG=,
∴S△AOB=AB?OG
=2×
=.
∴它的内接正六边形ABCDEF的面积是6S△AOB=6(cm2).
故选:C.
2.解:如图所示:
∵五边形ABCDE为正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,
∴∠CBD=∠CDB=∠CED=∠DCE==36°,
∴∠BFC=∠BDC+∠DCE=72°.
故选:C.
3.解:过O作OH⊥AB于H,
在正六边形ABCDEF中,∠AOB==60°,
∵OA=OB,
∴∠AOH=30°,AH=AB=1,
∴OH=AH=,
故选:C.
4.解:连接OA、OB、OC,如图,
∵AB,AC分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOC==90°,∠AOB==120°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∴n==12,
即BC恰好是同圆内接一个正十二边形的一边.
故选:C.
5.解:连接ON,过O作OH⊥FM于H,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,
∵OH⊥FM,OF=OM,
∴∠OFH=60°,∠OHF=90°,FH=FM=2,
∴OH=FH=2,
故选:C.
6.解:∵五边形ABCDE是正五边形,
∴∠E=∠A=180°﹣=108°.
∵AB、DE与⊙O相切,
∴∠OBA=∠ODE=90°,
∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,
故选:C.
7.解:∵正六边形ABCDEF内接于⊙O,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=3,
∴扇形AOB的面积==,
故选:B.
8.解:由题意得:正六边形的每个内角都等于120°,正方形的每个内角都等于90°,
故∠BAC=360°﹣120°﹣90°=150°,
∵AB=AC,
∴∠ABC=∠ACB==15°.
故选:B.
9.解:从O点出发,确定点O分别到A,B,C,D,E的距离,只有OA=OC=OD,
∵三角形的外心到三角形的三个顶点的距离相等,
∴点O是△ACD的外心,
故选:D.
10.解:延长DE交AG于T.
由题意FG=2EF,∠EFC=∠EFT=60°,
∵∠DEF=120°,
∴∠EFT=60°,
∴∠EFT=∠FET=∠ETF=60°,
∴EF=FT=ET,
∴TG=TF=ET,
∴∠FEG=90°,
∵AB=AF=EF=,
∴EG=EF?tan60°=3,
故选:C.
二.填空题
11.解:∵五边形ABCDE是正五边形,
∴五边形ABCDE为圆内接正五边形,
∴====,
∴∠BAE==108°,∠HAN=∠AEH=∠BAC=∠DAE=∠ABE=∠BAE=×108°=36°,
∴∠EAH=∠BAN=36°+36°=72°,
∴∠AHE=180°﹣72°﹣36°=72°,∠ANB=180°﹣72°﹣36°=72°,
∴∠EAH=∠EHA=72°,∠ANH=∠AHN=72°,
∴AE=HE,∠EAH=∠EHA=∠ANH=∠AHN,
∴△AEH∽△AHN,
∴=,
∵五角星的边框总长为40cm,
∴AH=AN=EN==4,HN=HE﹣NE=AE﹣4,
∴=,
整理得:(AE﹣2)2=20,
∴AE=2+2(cm),
故答案为:2+2.
12.解:如图所示:
作AM⊥CB于M,则AM=2,
∵六边形ABCDEF是正六边形,
∴∠ABC=120°,
∴∠ABM=180°﹣120°=60°,
∵sin∠ABM=,
∴AB===;
故答案为:.
13.解:设圆的半径为r,
如图①,∠AOB=×360°=120°,
∵OA=OB,
∴∠OAB=30°,
过点O作OC⊥AB于点C,
则AB=2AC,
∵AC=OA?cos30°=r,
∴AB=r;
如图②,∠AOB=×360°=90°,
∵OA=OB,
∴AB=OA=r;
如图③,∠AOB=×360°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴AB=OA=r;
∴同圆的内接正三边形、正四边形、正六边形的边长之比为:::1.
故答案为:::1.
14.解:∵正九边形内角和为(9﹣2)×180°=1260°,
∴每个内角为140°,
又∵AB=BC,∠B=140°,
∴∠CAB=(180°﹣140°)÷2=20°,
连接AH,作HM,GN分别垂直AE于M,N.
∵∠CAE=2∠CAB=2×20°=40°.
∴∠HAM=140°﹣2×20°﹣40°=60°,
∴∠AHM=30°,
设AM=EN=x,MN=y,
四边形HGNM是矩形,所以HG=y,即正九边形边长为y,
在Rt△AHM中,∠AHM=30°,
∴AC=AH=2AM=2x,
∴AB+AC=y+2x,
∵AE=AM+MN+EN=2x+y,
∴AE=AB+AC=3.
故答案为:3.
15.解:连接OE、OG,OF,
∵EF=a,且正六边形T1,
∴△OEF为等边三角形,OE为圆的半径r,
∴a:r=1:1;
由题意可知OG为∠FOE的平分线,即∠EOG=∠EOF=30°,
在Rt△OEG中,OE=r,OG=b,
∵==cos∠EOG=cos30°,即=,
∵r:a=1:1;r:b=:2;
故答案为:r:a=1:1;r:b=:2;
三.解答题
16.(1)解:∵六边形ABCDEF是正六边形,
∴∠FAB==120°;
(2)证明:连接OA、OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠FAB=∠CBA,
∴∠OAG=∠OBH,
在△AOG和△BOH中,
,
∴△AOG≌△BOH(SAS)
∴OG=OH.
17.解:(1)连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴n==12.
18.解:(1)首先把圆六等份,然后连接三个不相邻的顶点即可作出.
△ABC就是所求的三角形;
(2)在直角△ABD中,AD==,
则BC=AD=,CD=AB=x.
则矩形的周长是:2x+2,
故答案是:2x+2;
(3)连接AC,
∵AD是直径,
∴∠ACD=90°,
又∵CG⊥AD于点G.
∴CD2=DG?AD,
∴DG==,
∴BC=EF=AD﹣2DG=2r﹣.
则L=4x+4r﹣.
当x=﹣=r时,L取得最大值.最大值是:6r.
