人教版数学七年级下册 第5章 5.3平行线的性质同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第5章 5.3平行线的性质同步测试试题(一)(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 157.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-23 00:00:00 | ||
图片预览


文档简介
平行线的性质同步测试试题(一)
一.选择题
1.下列命题是假命题的是( )
A.矩形既是轴对称图形,又是中心对称图形
B.菱形的每一条对角线平分一组对角
C.对角线垂直且相等的四边形是正方形
D.50个学生中,很可能有两个学生的生日相同
2.下列命题正确的是( )
A.用科学记数法表示0.000000032,记为3.2×10﹣9
B.两边及一角对应相等的两个三角形全等
C.16的平方根是4
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.下列命题中,错误的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相平分且相等
C.正方形的两条对角线垂直平分且相等
D.等腰三角形底边上的中点到两腰的距离相等
4.下列命题中(1)三角形的角平分线、中线和高都是线段;(2)各边都相等的多边形是正多边形;(3)三角形的一个外角等于与任意两个内角的和;(4)若∠A+∠B=∠C,则△ABC是直角三角形.其中正确的个数是( )
A.1个
B.2
个
C.3个
D.4个
5.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA交于点N,那么=( )
A.
B.
C.
D.
6.下列命题中,其真命题个数有( )
①矩形的对角线互相垂直平分
②平行四边形的对角线互相平分
③正方形的对角线互相垂直平分且相等
④菱形的对角线相互平分且相等
A.4个
B.3个
C.2个
D.1个
7.下列说法中,不正确的个数是( )
①若a+b=0,则有a,b互为相反数,且=﹣1;②若|a|>|b|,则有(a+b)(a﹣b)是正数;③三个五次多项式的和也是五次多项式;④a+b+c<0,abc>0,则﹣+﹣的结果有三个;⑤方程ax+b=0(a,b为常数)是关于x的一元一次方程.
A.1个
B.2个
C.3个
D.4个
8.如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个
B.6个
C.7个
D.8个
9.如图,已知直线l交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=∠BAE,∠DBF=∠ABF,则∠ADB的度数是( )
A.45°
B.50°
C.60°
D.无法确定
10.下列各命题中,假命题是( )
A.有两边及其中一边上的中线对应相等的两个三角形全等
B.有两边及第三边上高对应相等的两个三角形全等
C.有两角及其中一角的平分线对应相等的两三角形全等
D.有两边及第三边上的中线对应相等的两三角形全等
二.填空题
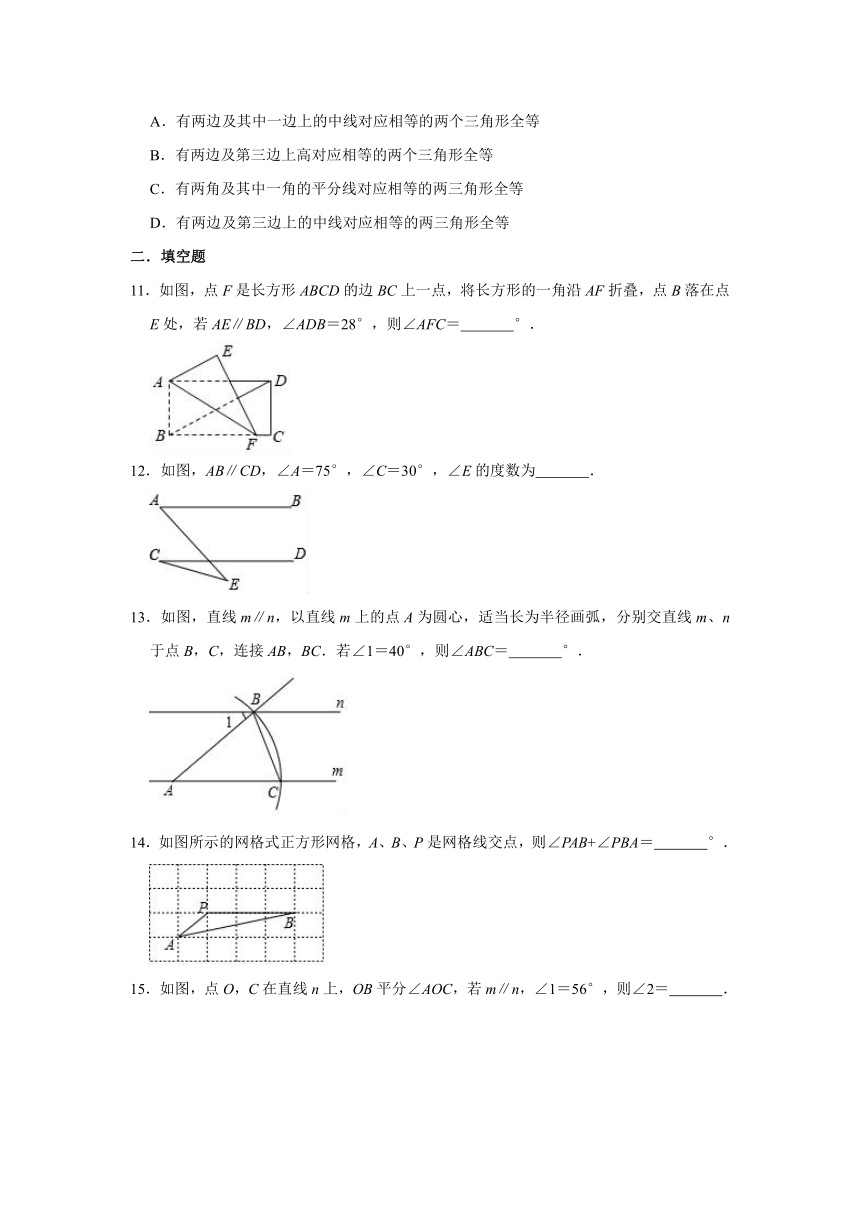
11.如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC=
°.
12.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为
.
13.如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m、n于点B,C,连接AB,BC.若∠1=40°,则∠ABC=
°.
14.如图所示的网格式正方形网格,A、B、P是网格线交点,则∠PAB+∠PBA=
°.
15.如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2=
.
三.解答题
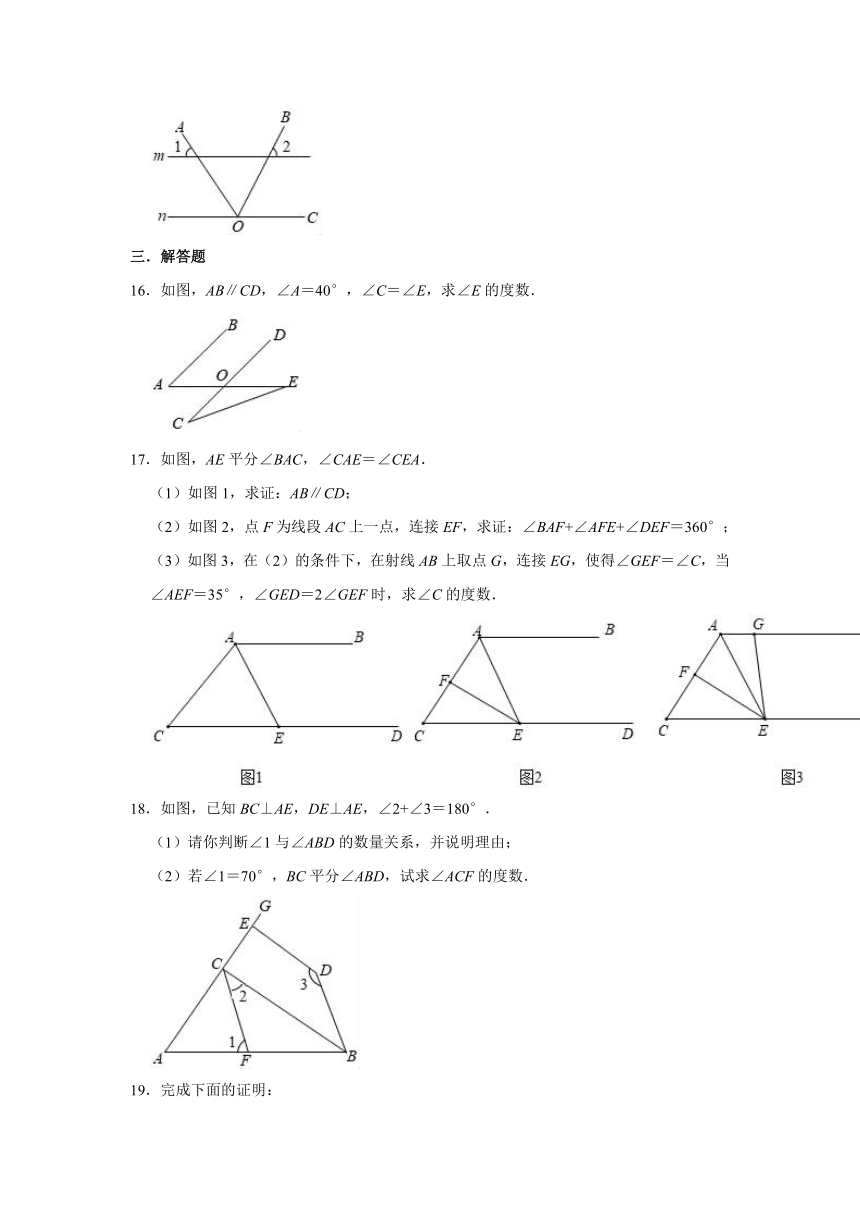
16.如图,AB∥CD,∠A=40°,∠C=∠E,求∠E的度数.
17.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
18.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.
(1)请你判断∠1与∠ABD的数量关系,并说明理由;
(2)若∠1=70°,BC平分∠ABD,试求∠ACF的度数.
19.完成下面的证明:
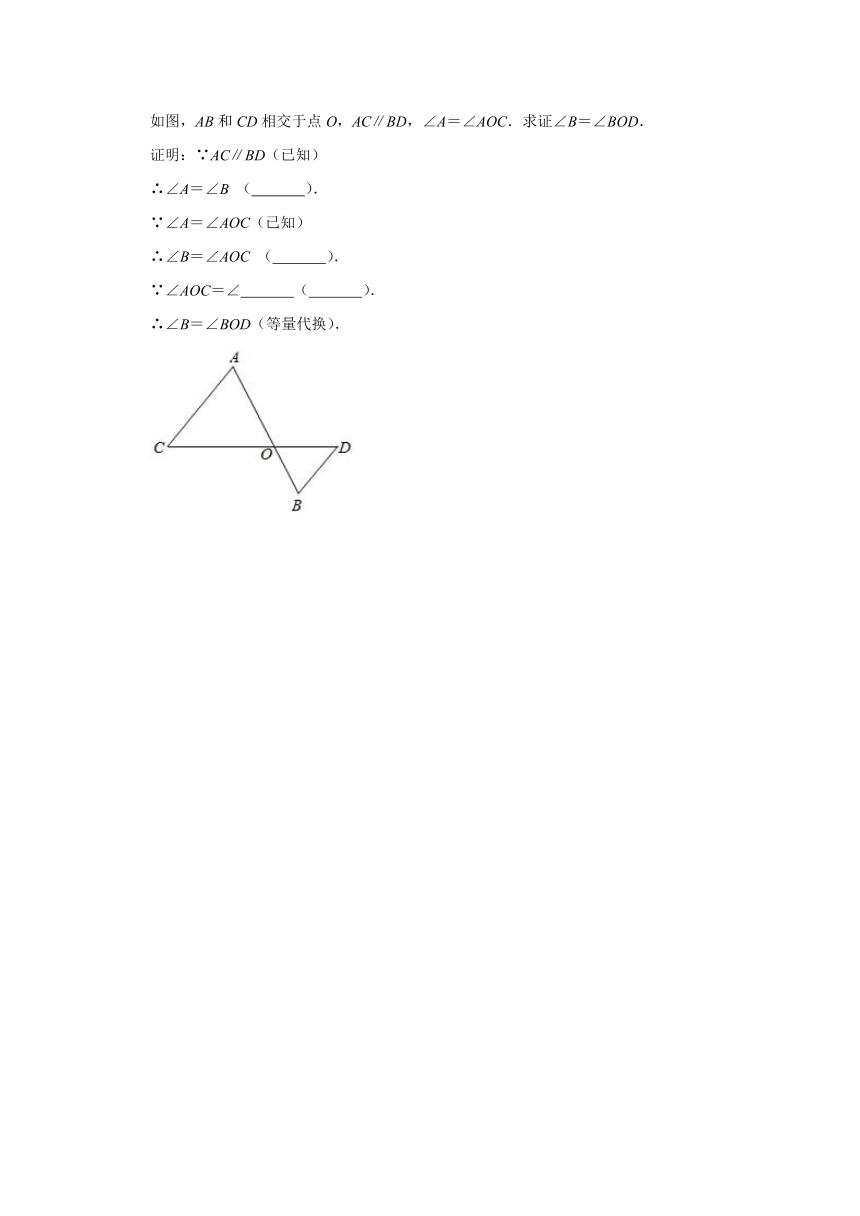
如图,AB和CD相交于点O,AC∥BD,∠A=∠AOC.求证∠B=∠BOD.
证明:∵AC∥BD(已知)
∴∠A=∠B
(
).
∵∠A=∠AOC(已知)
∴∠B=∠AOC
(
).
∵∠AOC=∠
(
).
∴∠B=∠BOD(等量代换).
参考答案与试题解析
一.选择题
1.【解答】解:A、矩形既是轴对称图形,又是中心对称图形,正确,是真命题,不符合题意;
B、菱形的每一条对角线平分一组对角,正确,是真命题,不符合题意;
C、对角线垂直且相等的平行四边形是正方形,故原命题错误,是假命题,符合题意;
D、50个学生中,很可能有两个学生的生日相同,正确,是真命题,不符合题意,
故选:C.
2.【解答】解:A、用科学记数法表示0.000000032,记为3.2×10﹣9,本选项说法正确;
B、两边及夹角对应相等的两个三角形全等,本选项说法错误;
C、16的平方根是±4,本选项说法错误;
D、一组对边平行,另一组对边相等的四边形是平行四边形或梯形,本选项说法错误;
故选:A.
3.【解答】解:A、对角线互相垂直的平行四边形是菱形,本选项说法错误,符合题意;
B、矩形的对角线互相平分且相等,本选项说法正确,不符合题意;
C、正方形的两条对角线垂直平分且相等,本选项说法正确,不符合题意;
D、等腰三角形底边上的中点到两腰的距离相等,本选项说法正确,不符合题意;
故选:A.
4.【解答】解:(1)三角形的角平分线、中线和高都是线段,是真命题;
(2)各边都相等且各个内角都相等的多边形是正多边形,原命题是假命题;
(3)三角形的一个外角等于与它不相邻的两个内角的和,原命题是假命题;
(4)若∠A+∠B=∠C,则△ABC是直角三角形,是真命题.
故选:B.
5.【解答】解:如图,过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PM,
∵PN∥OB,
∴∠POM=∠OPN,
∴∠PNE=∠PON+∠OPN=∠PON+∠POM=∠AOB=45°,
∴=.
故选:A.
6.【解答】解:①矩形的对角线互相平分,但不一定垂直,本小题说法是假命题;
②平行四边形的对角线互相平分,本小题说法是真命题;
③正方形的对角线互相垂直平分且相等,本小题说法是真命题;
④菱形的对角线相互平分,但不一定相等,本小题说法是假命题;
故选:C.
7.【解答】解:①若a+b=0,则有a,b互为相反数,当a=b=0时,无意义,本小题说法不正确;
②∵|a|>|b|,
∴a2>b2,
∴(a+b)(a﹣b)=a2﹣b2>0,是正数,本小题说法正确;
③(2a5+a﹣3)+(﹣a5+2a﹣3)+(﹣a5+a2﹣30)=a2+3a﹣36,
则三个五次多项式的和不一定是五次多项式,本小题说法不正确;
④当a+b+c<0,abc>0时,a、b、c两个正数、一个负数或一个正数、两个负数,
则﹣+﹣的结果有两个,本小题说法不正确;
⑤方程ax+b=0(a,b为常数),当a=0时,不是关于x的一元一次方程,本小题说法不正确;
故选:D.
8.【解答】解:∵AC∥DE,AB∥DF,
∴∠C=∠BDE,∠B=∠CDF,
又∵∠B=∠C,
∴∠C=∠BDE=∠B=∠CDF,
∵EF∥BC,
∴∠DEF=∠BDE,∠DFE=∠CDF,∠AEF=∠B,∠AFE=∠C,
∴与∠B相等的角为:∠BDE,∠CDF,∠C,∠DEF,∠DFE,∠AEF,∠AFE,
∴图中与∠B相等的角(∠B除外)有7个,
故选:C.
9.【解答】解:∵a∥b,
∴∠EAB+∠ABF=180°,
∵∠DAE=∠BAE,∠DBF=∠ABF,
∴∠DAB+∠ABD=×180°=135°,
∴∠ADB=180°﹣(∠DAB+∠ABD)=180°﹣135°=45°,
故选:A.
10.【解答】解:A、有两边及其中一边上的中线对应相等的两个三角形全等,可利用证两步全等的方法求得,是真命题;
B、高有可能在内部,也有可能在外部,是不确定的,不符合全等的条件,原命题是假命题;
C、有两角及其中一角的平分线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;
D、有两边及第三边上的中线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;
故选:B.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
∵AE∥BD,
∴∠DAE=∠ADB=28°,
∴∠BAE=∠BAD+∠DAE=90°+28°=118°,
∵矩形ABCD沿AF折叠,点B落在点E处,
∴∠BAF=∠EAF=∠BAE=×118°=59°,
∴∠AFC=∠BAF+∠ABF=59°+90°=149°.
故答案为149.
12.【解答】解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴∠AEF=∠A=75°,∠CEF=∠C=30°,
∴∠AEC=∠AEF﹣∠CEF=75°﹣30°=45°.
故答案为:45°.
13.【解答】解:∵m∥n,
∴(∠1+∠2)+∠3=180°,
∵AB=AC,
∴∠2=∠3,
∵∠1=40°,
∴40°+2∠2=180°,
解得∠2=70°,
即∠ABC=70°,
故答案为:70.
14.【解答】解:∵PB∥AC,
∴∠B=∠BAC,
∴∠PAB+∠PBA=∠PAB+∠BAC=∠PAC=45°,
故答案为:45.
15.【解答】解:如图,∵m∥n,∠1=56°,
∴∠1=∠3=56°,
∴∠AOC=180°﹣∠3=180°﹣56°=124°,
∵OB平分∠AOC,
∴∠4=∠5==,
∵m∥n,
∴∠2=∠5=62°,
故答案为:62°.
三.解答题(共4小题)
16.【解答】解:∵AB∥CD,∠A=40°,
∴∠A=∠DOE=40°,
∵∠DOE=∠C+∠E,
又∵∠E=∠C,
∴∠C=∠A=20°.
17.【解答】(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
18.【解答】解:(1)∠1=∠ABD,理由:
∵BC⊥AE,DE⊥AE,
∴BC∥DE,
∴∠3+∠CBD=180°,
又∵∠2+∠3=180°,
∴∠2=∠CBD,
∴CF∥DB,
∴∠1=∠ABD.
(2)∵∠1=70°,CF∥DB,
∴∠ABD=70°,
又∵BC平分∠ABD,
∴∠DBC=∠ABD=35°,
∴∠2=∠DBC=35°,
又∵BC⊥AG,
∴∠ACF=90°﹣∠2=90°﹣35°=55°.
19.【解答】证明:∵AC∥BD(已知)
∴∠A=∠B
(两直线平行,内错角相等).
∵∠A=∠AOC(已知)
∴∠B=∠AOC
(等量代换).
∵∠AOC=∠BOD(对顶角相等).
∴∠B=∠BOD(等量代换).
故答案为:两直线平行,内错角相等;等量代换;∠BOD,对顶角相等.
一.选择题
1.下列命题是假命题的是( )
A.矩形既是轴对称图形,又是中心对称图形
B.菱形的每一条对角线平分一组对角
C.对角线垂直且相等的四边形是正方形
D.50个学生中,很可能有两个学生的生日相同
2.下列命题正确的是( )
A.用科学记数法表示0.000000032,记为3.2×10﹣9
B.两边及一角对应相等的两个三角形全等
C.16的平方根是4
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.下列命题中,错误的是( )
A.对角线互相垂直的四边形是菱形
B.矩形的对角线互相平分且相等
C.正方形的两条对角线垂直平分且相等
D.等腰三角形底边上的中点到两腰的距离相等
4.下列命题中(1)三角形的角平分线、中线和高都是线段;(2)各边都相等的多边形是正多边形;(3)三角形的一个外角等于与任意两个内角的和;(4)若∠A+∠B=∠C,则△ABC是直角三角形.其中正确的个数是( )
A.1个
B.2
个
C.3个
D.4个
5.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA交于点N,那么=( )
A.
B.
C.
D.
6.下列命题中,其真命题个数有( )
①矩形的对角线互相垂直平分
②平行四边形的对角线互相平分
③正方形的对角线互相垂直平分且相等
④菱形的对角线相互平分且相等
A.4个
B.3个
C.2个
D.1个
7.下列说法中,不正确的个数是( )
①若a+b=0,则有a,b互为相反数,且=﹣1;②若|a|>|b|,则有(a+b)(a﹣b)是正数;③三个五次多项式的和也是五次多项式;④a+b+c<0,abc>0,则﹣+﹣的结果有三个;⑤方程ax+b=0(a,b为常数)是关于x的一元一次方程.
A.1个
B.2个
C.3个
D.4个
8.如图,AC∥DE,AB∥DF,EF∥BC,∠B=∠C,则图中与∠B相等的角(∠B除外)有( )
A.5个
B.6个
C.7个
D.8个
9.如图,已知直线l交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=∠BAE,∠DBF=∠ABF,则∠ADB的度数是( )
A.45°
B.50°
C.60°
D.无法确定
10.下列各命题中,假命题是( )
A.有两边及其中一边上的中线对应相等的两个三角形全等
B.有两边及第三边上高对应相等的两个三角形全等
C.有两角及其中一角的平分线对应相等的两三角形全等
D.有两边及第三边上的中线对应相等的两三角形全等
二.填空题
11.如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC=
°.
12.如图,AB∥CD,∠A=75°,∠C=30°,∠E的度数为
.
13.如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m、n于点B,C,连接AB,BC.若∠1=40°,则∠ABC=
°.
14.如图所示的网格式正方形网格,A、B、P是网格线交点,则∠PAB+∠PBA=
°.
15.如图,点O,C在直线n上,OB平分∠AOC,若m∥n,∠1=56°,则∠2=
.
三.解答题
16.如图,AB∥CD,∠A=40°,∠C=∠E,求∠E的度数.
17.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
18.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.
(1)请你判断∠1与∠ABD的数量关系,并说明理由;
(2)若∠1=70°,BC平分∠ABD,试求∠ACF的度数.
19.完成下面的证明:
如图,AB和CD相交于点O,AC∥BD,∠A=∠AOC.求证∠B=∠BOD.
证明:∵AC∥BD(已知)
∴∠A=∠B
(
).
∵∠A=∠AOC(已知)
∴∠B=∠AOC
(
).
∵∠AOC=∠
(
).
∴∠B=∠BOD(等量代换).
参考答案与试题解析
一.选择题
1.【解答】解:A、矩形既是轴对称图形,又是中心对称图形,正确,是真命题,不符合题意;
B、菱形的每一条对角线平分一组对角,正确,是真命题,不符合题意;
C、对角线垂直且相等的平行四边形是正方形,故原命题错误,是假命题,符合题意;
D、50个学生中,很可能有两个学生的生日相同,正确,是真命题,不符合题意,
故选:C.
2.【解答】解:A、用科学记数法表示0.000000032,记为3.2×10﹣9,本选项说法正确;
B、两边及夹角对应相等的两个三角形全等,本选项说法错误;
C、16的平方根是±4,本选项说法错误;
D、一组对边平行,另一组对边相等的四边形是平行四边形或梯形,本选项说法错误;
故选:A.
3.【解答】解:A、对角线互相垂直的平行四边形是菱形,本选项说法错误,符合题意;
B、矩形的对角线互相平分且相等,本选项说法正确,不符合题意;
C、正方形的两条对角线垂直平分且相等,本选项说法正确,不符合题意;
D、等腰三角形底边上的中点到两腰的距离相等,本选项说法正确,不符合题意;
故选:A.
4.【解答】解:(1)三角形的角平分线、中线和高都是线段,是真命题;
(2)各边都相等且各个内角都相等的多边形是正多边形,原命题是假命题;
(3)三角形的一个外角等于与它不相邻的两个内角的和,原命题是假命题;
(4)若∠A+∠B=∠C,则△ABC是直角三角形,是真命题.
故选:B.
5.【解答】解:如图,过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PM,
∵PN∥OB,
∴∠POM=∠OPN,
∴∠PNE=∠PON+∠OPN=∠PON+∠POM=∠AOB=45°,
∴=.
故选:A.
6.【解答】解:①矩形的对角线互相平分,但不一定垂直,本小题说法是假命题;
②平行四边形的对角线互相平分,本小题说法是真命题;
③正方形的对角线互相垂直平分且相等,本小题说法是真命题;
④菱形的对角线相互平分,但不一定相等,本小题说法是假命题;
故选:C.
7.【解答】解:①若a+b=0,则有a,b互为相反数,当a=b=0时,无意义,本小题说法不正确;
②∵|a|>|b|,
∴a2>b2,
∴(a+b)(a﹣b)=a2﹣b2>0,是正数,本小题说法正确;
③(2a5+a﹣3)+(﹣a5+2a﹣3)+(﹣a5+a2﹣30)=a2+3a﹣36,
则三个五次多项式的和不一定是五次多项式,本小题说法不正确;
④当a+b+c<0,abc>0时,a、b、c两个正数、一个负数或一个正数、两个负数,
则﹣+﹣的结果有两个,本小题说法不正确;
⑤方程ax+b=0(a,b为常数),当a=0时,不是关于x的一元一次方程,本小题说法不正确;
故选:D.
8.【解答】解:∵AC∥DE,AB∥DF,
∴∠C=∠BDE,∠B=∠CDF,
又∵∠B=∠C,
∴∠C=∠BDE=∠B=∠CDF,
∵EF∥BC,
∴∠DEF=∠BDE,∠DFE=∠CDF,∠AEF=∠B,∠AFE=∠C,
∴与∠B相等的角为:∠BDE,∠CDF,∠C,∠DEF,∠DFE,∠AEF,∠AFE,
∴图中与∠B相等的角(∠B除外)有7个,
故选:C.
9.【解答】解:∵a∥b,
∴∠EAB+∠ABF=180°,
∵∠DAE=∠BAE,∠DBF=∠ABF,
∴∠DAB+∠ABD=×180°=135°,
∴∠ADB=180°﹣(∠DAB+∠ABD)=180°﹣135°=45°,
故选:A.
10.【解答】解:A、有两边及其中一边上的中线对应相等的两个三角形全等,可利用证两步全等的方法求得,是真命题;
B、高有可能在内部,也有可能在外部,是不确定的,不符合全等的条件,原命题是假命题;
C、有两角及其中一角的平分线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;
D、有两边及第三边上的中线对应相等的两三角形全等,可利用证两步全等的方法求得,是真命题;
故选:B.
二.填空题(共5小题)
11.【解答】解:∵四边形ABCD为矩形,
∴∠BAD=∠ABC=90°,
∵AE∥BD,
∴∠DAE=∠ADB=28°,
∴∠BAE=∠BAD+∠DAE=90°+28°=118°,
∵矩形ABCD沿AF折叠,点B落在点E处,
∴∠BAF=∠EAF=∠BAE=×118°=59°,
∴∠AFC=∠BAF+∠ABF=59°+90°=149°.
故答案为149.
12.【解答】解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,EF∥CD,
∴∠AEF=∠A=75°,∠CEF=∠C=30°,
∴∠AEC=∠AEF﹣∠CEF=75°﹣30°=45°.
故答案为:45°.
13.【解答】解:∵m∥n,
∴(∠1+∠2)+∠3=180°,
∵AB=AC,
∴∠2=∠3,
∵∠1=40°,
∴40°+2∠2=180°,
解得∠2=70°,
即∠ABC=70°,
故答案为:70.
14.【解答】解:∵PB∥AC,
∴∠B=∠BAC,
∴∠PAB+∠PBA=∠PAB+∠BAC=∠PAC=45°,
故答案为:45.
15.【解答】解:如图,∵m∥n,∠1=56°,
∴∠1=∠3=56°,
∴∠AOC=180°﹣∠3=180°﹣56°=124°,
∵OB平分∠AOC,
∴∠4=∠5==,
∵m∥n,
∴∠2=∠5=62°,
故答案为:62°.
三.解答题(共4小题)
16.【解答】解:∵AB∥CD,∠A=40°,
∴∠A=∠DOE=40°,
∵∠DOE=∠C+∠E,
又∵∠E=∠C,
∴∠C=∠A=20°.
17.【解答】(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFE=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
18.【解答】解:(1)∠1=∠ABD,理由:
∵BC⊥AE,DE⊥AE,
∴BC∥DE,
∴∠3+∠CBD=180°,
又∵∠2+∠3=180°,
∴∠2=∠CBD,
∴CF∥DB,
∴∠1=∠ABD.
(2)∵∠1=70°,CF∥DB,
∴∠ABD=70°,
又∵BC平分∠ABD,
∴∠DBC=∠ABD=35°,
∴∠2=∠DBC=35°,
又∵BC⊥AG,
∴∠ACF=90°﹣∠2=90°﹣35°=55°.
19.【解答】证明:∵AC∥BD(已知)
∴∠A=∠B
(两直线平行,内错角相等).
∵∠A=∠AOC(已知)
∴∠B=∠AOC
(等量代换).
∵∠AOC=∠BOD(对顶角相等).
∴∠B=∠BOD(等量代换).
故答案为:两直线平行,内错角相等;等量代换;∠BOD,对顶角相等.
