华师大版八年级下册数学 16.1.1分式教案
文档属性
| 名称 | 华师大版八年级下册数学 16.1.1分式教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 197.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 00:00:00 | ||
图片预览


文档简介
§16.1.1 分式
教 学
目
标 知识 1 使学生经历分式概念的形成过程,了解分式、整式、有理式的概念及它们区别与联系.
2 使学生掌握分式有意义的条件,认识事物的联系与制约关系.
3 培养学生对事物用类比的思想方法进行探索分析.
能力
情感
教学 重点 了解分式的形式(A、B是整式)并理解分式概念中的“一个特点”:分母含有字母;“一个要求”:字母的取值要使分母的值不能为零;
教学 难点 理解分式中的分母含有字母以及字母的取值要使分母的值不能为零.
学情 分析 通过对分数的回顾,学生可能会用分数的定义去理解分式.但是在分式中,它的分母不是具体的数,而是含有字母的整式。为了学生能切实掌握所学知识,在教学中对于教材中的例题和练习题,作了适当的延伸拓展和变式处理.还特别设计了反馈练习。
教学 准备 课件,多媒体
学 案 一 学习目标
1 分式的定义:形如(A、B是 ,且B中含有 ,B≠ )的式子,叫做分式.
2 分式有意义B≠ ;分式没有意义B = ;分式的值为0A = 且 B≠ .
3 有理式的定义: 和 统称有理式.与有理数类似,有理式的如何分类?
二 自主学习
1 把下列有理式中是分式的代号填在横线上 .
(1)-3x; (2); (3); (4)-; (5) ;
(6); (7)-; (8); (9); (10).
2 当a 时,分式有意义.
3 当x 时,分式无意义.
4 当x 时,分式的值为零.
5 当x 时,分式的值为整数.
6 当x取什么数时,分式,(1)有意义 (2)值为零?
教学 过程 教 学 内 容 师 生 互 动 备 注
一 、
创
设
情
境
引
入
新
课 请你来填一填:
(1)面积为2平方米的长方形一边长3米,则它的另一边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一边长为_______米;
(3)已知正方形的周长是a cm,则一边的长是____cm,面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每 千克苹果的售价是______元.
讨论:
两个整数相除,不能整除时结果可用分数表示,当两个整式不能整除时,它们的商怎么表示呢?
解答:
(1)
(2)
(3)、
(4)
创设情景,提出问题,从实际问题引入,体现了数学源于生活,激发学生的求知欲望.
二 、
合
作
交
流
自
主
探
究 探究1:
、、、、
在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?
我们在小学学习分数时,把两个整数相除,如2÷3,可表示为的形式,并把叫做分数。类似地,如果用A、B表示两个整式,A÷B可表示成的形式,若B中含有字母,且B≠0,式子叫做分式。
探究2:
到本节课,我们一共学习了哪些代数式呢?它们之间有何关系?请同学们讨论一下!
如整数和分数我们统称有理数。
请同学猜测一下:
整式和分式我们统称 。
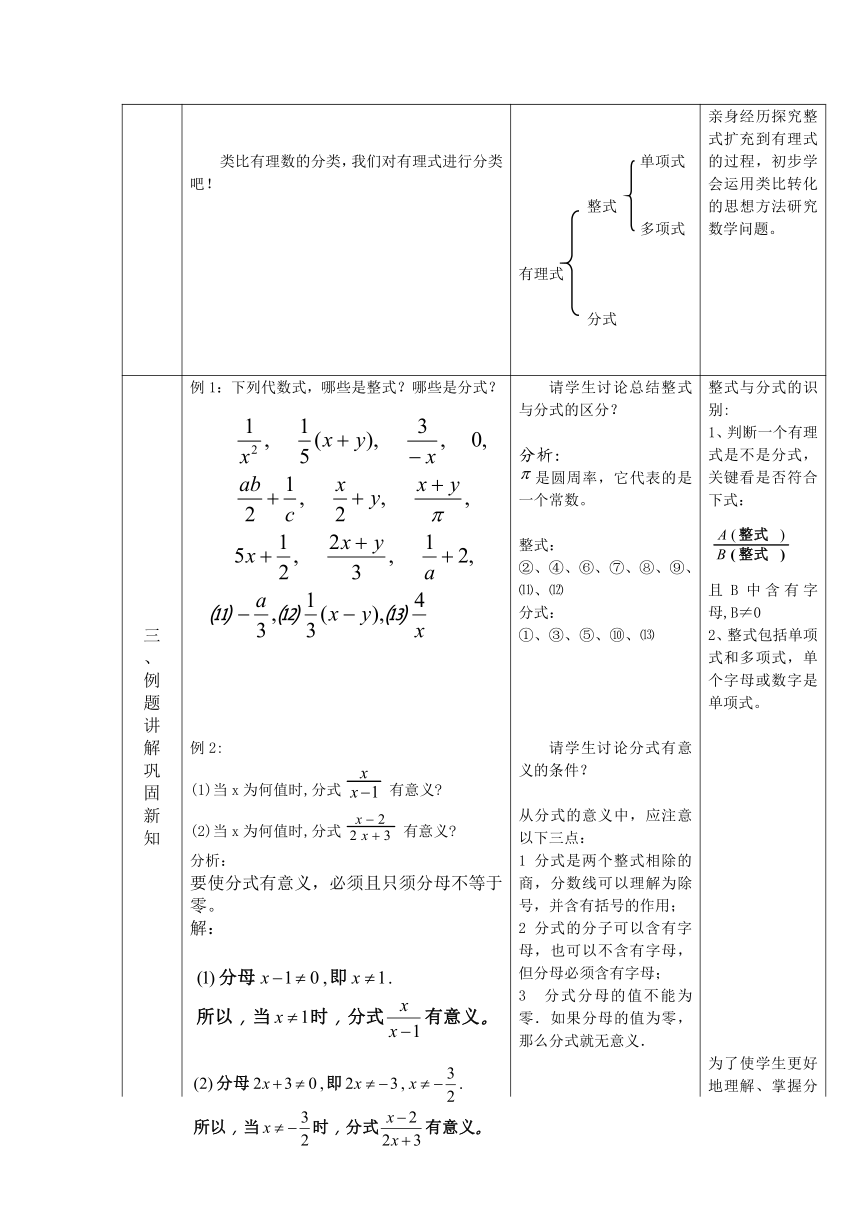
类比有理数的分类,我们对有理式进行分类吧!
讨论:
整式有①③④ ,整式的特点是分母不含字母;②⑤,这两个代数式不同于前面学过的整式,是两个分母含有字母的代数式.在实际应用中,某些数量关系只用整式来表示是不够的,因此,我们需要学习新的式子,以满足解决实际问题的需求.
分式的概念:即形如 (A、B是整式,且B中含有字母,B≠0)的式子叫分式。
学生探讨:
单项式、多项式、整式、分式
整式和分式统称为有理式。
单项式
整式
多项式
有理式
分式
探究的代数式,有些不是我们学过的整式,产生认知冲突,激发学习新知识的兴趣,以满足解决实际问题的需求。
要求学生探索识别分式的要点,分组讨论。
通过对分式与分数的类比,学生亲身经历探究整式扩充到有理式的过程,初步学会运用类比转化的思想方法研究数学问题。
三 、
例
题
讲
解
巩
固
新
知 例1:下列代数式,哪些是整式?哪些是分式?
例2:
(1)当x为何值时,分式有意义?
(2)当x为何值时,分式有意义?
分析:
要使分式有意义,必须且只须分母不等于零。
解:
例3:
当x为何值时,分式无意义?
解:
例4:
当y取什么值时,分式的值是零?
分析:
分式的值为0
①分子=0 ②代入分母≠0 ③最后答案
请学生讨论总结整式与分式的区分?
分析:
是圆周率,它代表的是一个常数。
整式:
②、④、⑥、⑦、⑧、⑨、⑾、⑿
分式:
①、③、⑤、⑩、⒀
请学生讨论分式有意义的条件?
从分式的意义中,应注意以下三点:
1 分式是两个整式相除的商,分数线可以理解为除号,并含有括号的作用;
2 分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母;
3 分式分母的值不能为零.如果分母的值为零,那么分式就无意义.
请学生讨论分式无意义的条件?
请学生讨论,什么条件下,才能保证分式的值为0?
解:
使得分式的值为0,则2y+1=0
∴y =
② 使得分式有意义,则4y-1≠0
∴y ≠
∴当y = 时,此分式的值是零。 整式与分式的识别:
1、判断一个有理式是不是分式,关键看是否符合下式:
且B中含有字母,B≠0
2、整式包括单项式和多项式,单个字母或数字是单项式。
为了使学生更好地理解、掌握分式的基本概念,例题设计的考虑:
例1 区分整式和分式;
例2 求分式有意义的条件;
例3 分式无意义的条件;
例4 是如何求分式的值为0.
四 、
目
标
检
测
形
成
练
习 请你来做一做:
1、当x为何值时,代数式有意义?
2、当x为何值时,代数式有意义?
3、当x为何值时,代数式有意义?
变题:当x为何值时,上面这些代数式无意义呢?
请学生解答在自己的草稿纸上,然后把部分学生的解答进行展示,发现学生的解答错误,及时纠正;发现亮点进行表扬。
五 、
课
堂
小
结
提
高
认
识
1、我们学习了什么新知识?
2、你有什么收获?
3、本节课你的最大疑惑是什么?
1 分式的定义:
整式A、B相除可写为的形式,若分母中含有字母,那么叫做分式。
2 分式的意义:
分母≠0
3 分式的值为0:
①分子=0 ②代入分母≠0 ③最后答案
六 、
巩
固
提
高
运
用
拓
展
1、当x为何值时,代数式有意义?
2、当x为何值时,分式无意义?
3、当x为何值时,分式的值为零?
4、x为何整数时,分式的值为整数?
5、若分式的值为0,则x的值是多少?
第5题分析:
① |x|-3 = 0
|x| = 3
∴x =±3
② 把x= - 3 代入,分母为0,分式没有意义
把x=3代入,分母等于12
∴ 当x = 3时,此分式值为0。
板 书
设
计
例 1 …… 例2 …… 例3 ……
教 学 反 思
1 在教学过程中要注意:通过对分式与分数的类比,学生亲身经历探究整式扩充到有理式的过程,初步学会运用类比转化的思想方法研究数学问题。 2 要注重联系实际探究分式的概念,通过分式概念的形成、分式有意义的条件等探讨活动,让学生亲身经历发现事物特征、规律的过程,激发他们的学习兴趣,引发他们自主学习的动机。同时,增强学生的探究意识和合作学习能力。
3 分式的概念一定要给学生讲透,使学生能熟练解答整式与分式的区分,分式有意义,分式无意义,分式的值为0,这四类题目。
4 (1)分式有意义?
即,, 结论中的“且”一般学生都要写成“或”,“且”是指同时保证,此题为易错题。
(2)分式无意义?
即,, 因为分式无意义,所以只要保证两者中的一个即可,当然用“或”。
这两个题目一定要给学生讲明,讲透。
可以给学生布置一个课后思考题:
若,则A、B应满足什么条件? 若,则A、B应满足什么条件?
教 学
目
标 知识 1 使学生经历分式概念的形成过程,了解分式、整式、有理式的概念及它们区别与联系.
2 使学生掌握分式有意义的条件,认识事物的联系与制约关系.
3 培养学生对事物用类比的思想方法进行探索分析.
能力
情感
教学 重点 了解分式的形式(A、B是整式)并理解分式概念中的“一个特点”:分母含有字母;“一个要求”:字母的取值要使分母的值不能为零;
教学 难点 理解分式中的分母含有字母以及字母的取值要使分母的值不能为零.
学情 分析 通过对分数的回顾,学生可能会用分数的定义去理解分式.但是在分式中,它的分母不是具体的数,而是含有字母的整式。为了学生能切实掌握所学知识,在教学中对于教材中的例题和练习题,作了适当的延伸拓展和变式处理.还特别设计了反馈练习。
教学 准备 课件,多媒体
学 案 一 学习目标
1 分式的定义:形如(A、B是 ,且B中含有 ,B≠ )的式子,叫做分式.
2 分式有意义B≠ ;分式没有意义B = ;分式的值为0A = 且 B≠ .
3 有理式的定义: 和 统称有理式.与有理数类似,有理式的如何分类?
二 自主学习
1 把下列有理式中是分式的代号填在横线上 .
(1)-3x; (2); (3); (4)-; (5) ;
(6); (7)-; (8); (9); (10).
2 当a 时,分式有意义.
3 当x 时,分式无意义.
4 当x 时,分式的值为零.
5 当x 时,分式的值为整数.
6 当x取什么数时,分式,(1)有意义 (2)值为零?
教学 过程 教 学 内 容 师 生 互 动 备 注
一 、
创
设
情
境
引
入
新
课 请你来填一填:
(1)面积为2平方米的长方形一边长3米,则它的另一边长为_______米;
(2)面积为S平方米的长方形一边长a米,则它的另一边长为_______米;
(3)已知正方形的周长是a cm,则一边的长是____cm,面积是_______cm2;
(4)一箱苹果售价P元,总重m千克,箱重n千克,则每 千克苹果的售价是______元.
讨论:
两个整数相除,不能整除时结果可用分数表示,当两个整式不能整除时,它们的商怎么表示呢?
解答:
(1)
(2)
(3)、
(4)
创设情景,提出问题,从实际问题引入,体现了数学源于生活,激发学生的求知欲望.
二 、
合
作
交
流
自
主
探
究 探究1:
、、、、
在上面所列出的代数式中,哪些是整式?哪些不是?它们之间有什么区别?
我们在小学学习分数时,把两个整数相除,如2÷3,可表示为的形式,并把叫做分数。类似地,如果用A、B表示两个整式,A÷B可表示成的形式,若B中含有字母,且B≠0,式子叫做分式。
探究2:
到本节课,我们一共学习了哪些代数式呢?它们之间有何关系?请同学们讨论一下!
如整数和分数我们统称有理数。
请同学猜测一下:
整式和分式我们统称 。
类比有理数的分类,我们对有理式进行分类吧!
讨论:
整式有①③④ ,整式的特点是分母不含字母;②⑤,这两个代数式不同于前面学过的整式,是两个分母含有字母的代数式.在实际应用中,某些数量关系只用整式来表示是不够的,因此,我们需要学习新的式子,以满足解决实际问题的需求.
分式的概念:即形如 (A、B是整式,且B中含有字母,B≠0)的式子叫分式。
学生探讨:
单项式、多项式、整式、分式
整式和分式统称为有理式。
单项式
整式
多项式
有理式
分式
探究的代数式,有些不是我们学过的整式,产生认知冲突,激发学习新知识的兴趣,以满足解决实际问题的需求。
要求学生探索识别分式的要点,分组讨论。
通过对分式与分数的类比,学生亲身经历探究整式扩充到有理式的过程,初步学会运用类比转化的思想方法研究数学问题。
三 、
例
题
讲
解
巩
固
新
知 例1:下列代数式,哪些是整式?哪些是分式?
例2:
(1)当x为何值时,分式有意义?
(2)当x为何值时,分式有意义?
分析:
要使分式有意义,必须且只须分母不等于零。
解:
例3:
当x为何值时,分式无意义?
解:
例4:
当y取什么值时,分式的值是零?
分析:
分式的值为0
①分子=0 ②代入分母≠0 ③最后答案
请学生讨论总结整式与分式的区分?
分析:
是圆周率,它代表的是一个常数。
整式:
②、④、⑥、⑦、⑧、⑨、⑾、⑿
分式:
①、③、⑤、⑩、⒀
请学生讨论分式有意义的条件?
从分式的意义中,应注意以下三点:
1 分式是两个整式相除的商,分数线可以理解为除号,并含有括号的作用;
2 分式的分子可以含有字母,也可以不含有字母,但分母必须含有字母;
3 分式分母的值不能为零.如果分母的值为零,那么分式就无意义.
请学生讨论分式无意义的条件?
请学生讨论,什么条件下,才能保证分式的值为0?
解:
使得分式的值为0,则2y+1=0
∴y =
② 使得分式有意义,则4y-1≠0
∴y ≠
∴当y = 时,此分式的值是零。 整式与分式的识别:
1、判断一个有理式是不是分式,关键看是否符合下式:
且B中含有字母,B≠0
2、整式包括单项式和多项式,单个字母或数字是单项式。
为了使学生更好地理解、掌握分式的基本概念,例题设计的考虑:
例1 区分整式和分式;
例2 求分式有意义的条件;
例3 分式无意义的条件;
例4 是如何求分式的值为0.
四 、
目
标
检
测
形
成
练
习 请你来做一做:
1、当x为何值时,代数式有意义?
2、当x为何值时,代数式有意义?
3、当x为何值时,代数式有意义?
变题:当x为何值时,上面这些代数式无意义呢?
请学生解答在自己的草稿纸上,然后把部分学生的解答进行展示,发现学生的解答错误,及时纠正;发现亮点进行表扬。
五 、
课
堂
小
结
提
高
认
识
1、我们学习了什么新知识?
2、你有什么收获?
3、本节课你的最大疑惑是什么?
1 分式的定义:
整式A、B相除可写为的形式,若分母中含有字母,那么叫做分式。
2 分式的意义:
分母≠0
3 分式的值为0:
①分子=0 ②代入分母≠0 ③最后答案
六 、
巩
固
提
高
运
用
拓
展
1、当x为何值时,代数式有意义?
2、当x为何值时,分式无意义?
3、当x为何值时,分式的值为零?
4、x为何整数时,分式的值为整数?
5、若分式的值为0,则x的值是多少?
第5题分析:
① |x|-3 = 0
|x| = 3
∴x =±3
② 把x= - 3 代入,分母为0,分式没有意义
把x=3代入,分母等于12
∴ 当x = 3时,此分式值为0。
板 书
设
计
例 1 …… 例2 …… 例3 ……
教 学 反 思
1 在教学过程中要注意:通过对分式与分数的类比,学生亲身经历探究整式扩充到有理式的过程,初步学会运用类比转化的思想方法研究数学问题。 2 要注重联系实际探究分式的概念,通过分式概念的形成、分式有意义的条件等探讨活动,让学生亲身经历发现事物特征、规律的过程,激发他们的学习兴趣,引发他们自主学习的动机。同时,增强学生的探究意识和合作学习能力。
3 分式的概念一定要给学生讲透,使学生能熟练解答整式与分式的区分,分式有意义,分式无意义,分式的值为0,这四类题目。
4 (1)分式有意义?
即,, 结论中的“且”一般学生都要写成“或”,“且”是指同时保证,此题为易错题。
(2)分式无意义?
即,, 因为分式无意义,所以只要保证两者中的一个即可,当然用“或”。
这两个题目一定要给学生讲明,讲透。
可以给学生布置一个课后思考题:
若,则A、B应满足什么条件? 若,则A、B应满足什么条件?
