北师大版八年级上册第七章 平行线的证明学案(表格式)
文档属性
| 名称 | 北师大版八年级上册第七章 平行线的证明学案(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 434.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 19:54:25 | ||
图片预览



文档简介
平行线的证明
学生姓名
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
平行线
教学目标
1、理解平行线的概念;掌握多边形的内角和公式以及多边形外角和公式。
2、掌握平行线的公理及其推论;理解内角和定理的推导。
3、能熟练掌握平行线的应用。
教学重点与难点
重点:理解平行线的概念;掌握多边形的内角和公式以及多边形外角和公式。
难点:掌握平行线的公理及其推论;理解内角和定理的推导。
知识点一、定义与命题
1、命题含义(情景引入)
活动内容:
如果B处水流受到污染,那么____处水流便受到污染;
如果C处水流受到污染,那么____处水流便受到污染;
如果D处水流受到污染,那么____处水流便受到污染;
如果____处水流受到污染,那么____处水流便受到污染.
在假设的前提条件下,对某一处受到污染作出了判断,像这样,对事情作出判断的句子,就叫做命题.
命题的定义:命题是判断一件事情的句子.
如:熊猫没有翅膀.对顶角相等.
举例
两直线平行,内错角相等.
无论n为任意的自然数,式子n2-n+11的值都是质数.
内错角相等.
任意一个三角形都有一个直角.
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
全等三角形的对应角相等.
……
注意:
你喜欢数学吗?
作线段AB=a.
平行用符号“∥”表示.
这些句子没有对某一件事情作出任何判断,那么它们就不是命题.
一般情况下:疑问句不是命题.图形的作法不是命题.)
2、探讨
①
探讨命题的结构特征
观察下列命题,发现它们的结构有什么共同特征?
(1)如果两个三角形的三条边对应相等,那么这两个三角形全等.
(2)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
(3)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形.
(4)如果一个四边的对角线相等,那么这个四边形是矩形.
(5)如果一个四边形的两条对角线互相垂直,那么这个四边形是菱形.
②
总结命题的结构特征
(1)上述命题都是“如果……,那么……”的形式.
(2)“如果……”是已知的事项,“那么……”是由已知事项推断出的结论.
(3)一般地命题都可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的结论,每个命题都有条件和结论.
3、定义与命题
①
定义的含义:对名称和术语的含义加以描述,作出明确的规定,就是它们的定义;
②
命题的含义:判断一件事情的句子,叫做命题,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
知识点二、相交线
1、相交线
在同一平面内,两条直线的位置关系有平行和相交。
(2)相交:在同一平面内,有一个公共点的两条直线称为相交线。
(3)邻补角与对顶角
定义:有公共顶点,且有一条公共边,另一条边互为反向延长线,具有这种位置关系的两个角,互为邻补角。邻补角互补。
定义:有一个公共顶点,并且有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角。对顶角相等。
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
图形顶点边的关系大小关系对顶角
∠1与∠2有公共顶点∠1的两边与∠2的两边互为反向延长线对顶角相等
即∠1=∠2邻补角
∠3与∠4
有公共顶点∠3与∠4有一条边公共,另一边互为反向延长线。∠3+∠4=180°
注意:(1)对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
(2)如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
(3)如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2.垂线
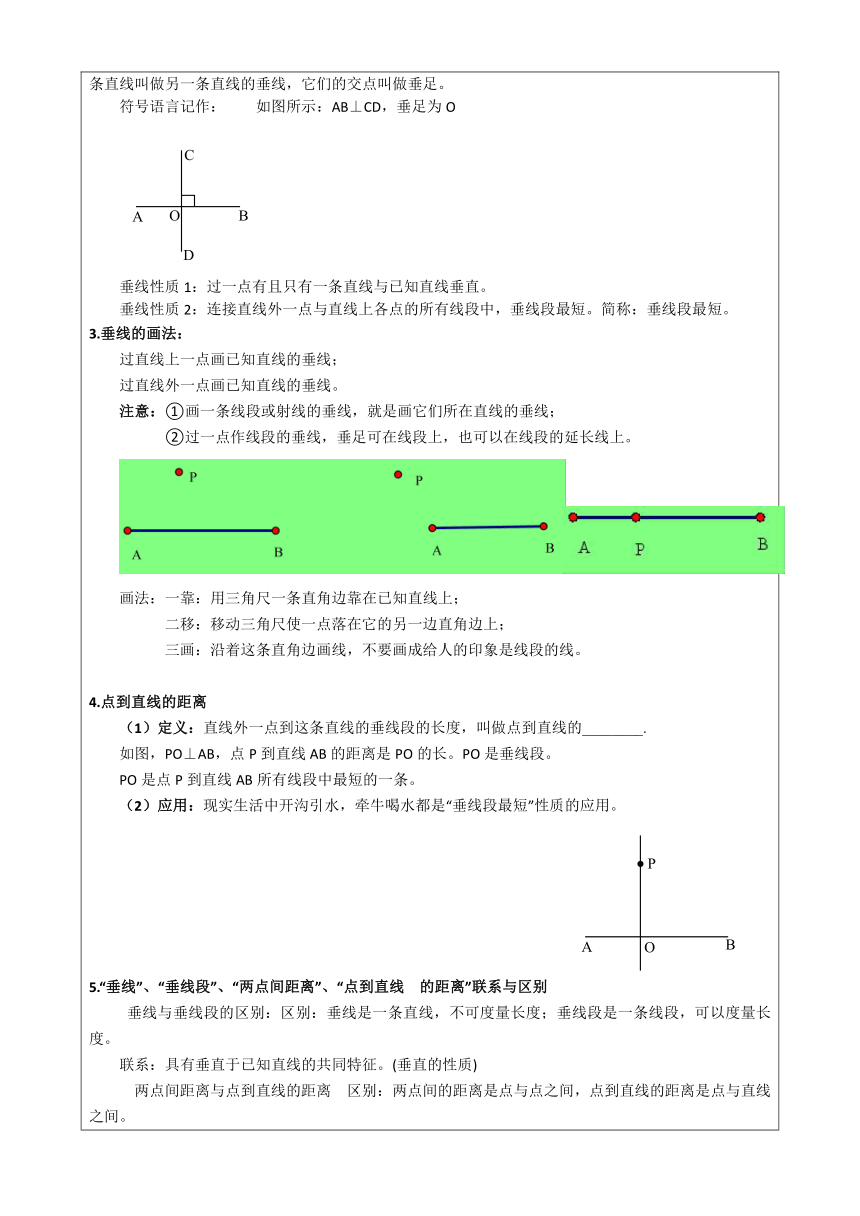
定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:
如图所示:AB⊥CD,垂足为O
垂线性质1:过一点有且只有一条直线与已知直线垂直。
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
3.垂线的画法:
过直线上一点画已知直线的垂线;
过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;
②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:一靠:用三角尺一条直角边靠在已知直线上;
二移:移动三角尺使一点落在它的另一边直角边上;
三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4.点到直线的距离
(1)定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的________.
如图,PO⊥AB,点P到直线AB的距离是PO的长。PO是垂线段。
PO是点P到直线AB所有线段中最短的一条。
(2)应用:现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
5.“垂线”、“垂线段”、“两点间距离”、“点到直线
的距离”联系与区别
垂线与垂线段的区别:区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。
联系:具有垂直于已知直线的共同特征。(垂直的性质)
两点间距离与点到直线的距离
区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。
联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
线段与距离
距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
三线八角
两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
如图,直线被直线所截
(1)∠1与∠5在截线的同侧,同在被截直线的上方,
叫做__________(位置相同)
(2)∠5与∠3在截线的两旁(交错),在被截直线之间(内),叫做_________(位置在内且交错)
(3)∠5与∠4在截线的同侧,在被截直线之间(内),叫做____________。
(4)三线八角也可以成模型中看出。同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
知识点三、平行线
1.平行线的概念
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥”表示,如“AB∥CD”,读作“AB平行于CD”。
同一平面内,两条直线的位置关系只有两种:平行或相交。
注意:
(1)平行线是无限延伸的,无论怎样延伸也不相交。
(2)当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
2.平行线公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
3.平行线的性质
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
练一练
1、如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为
.
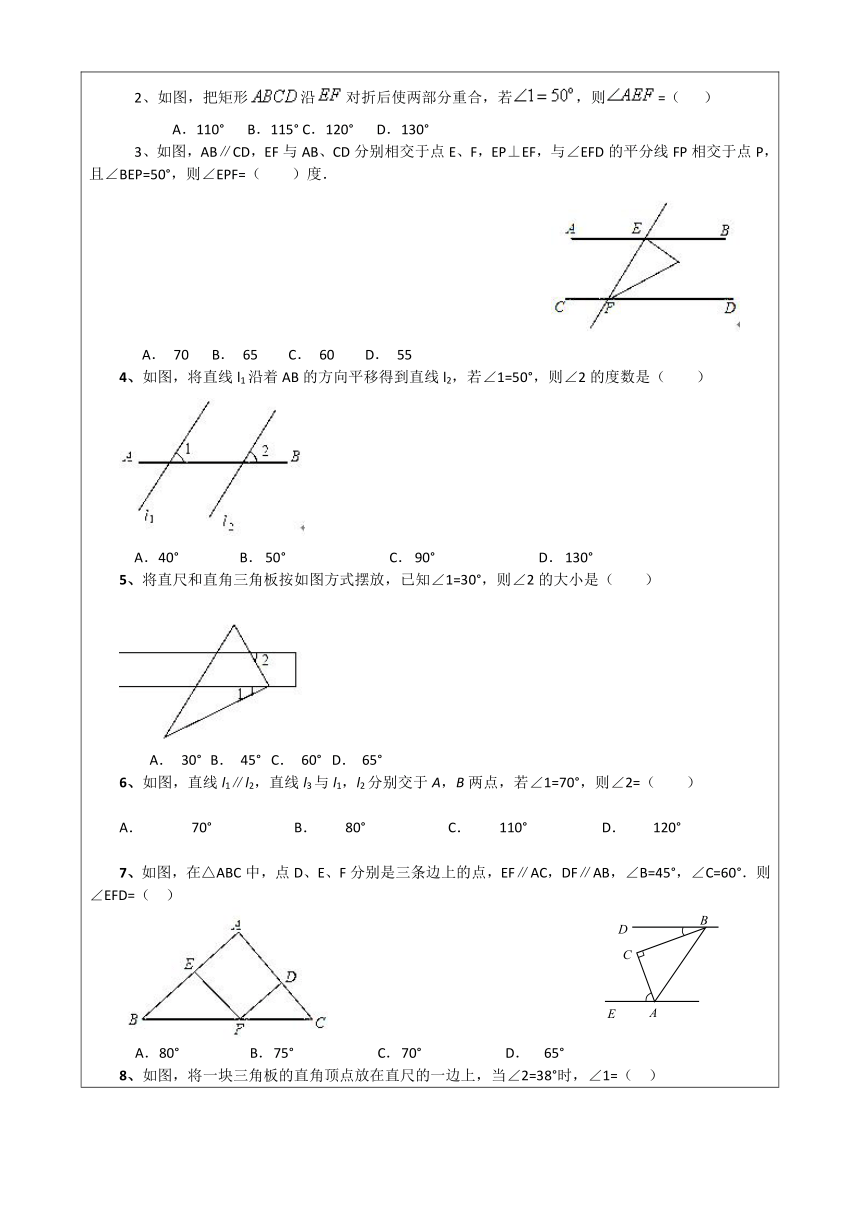
2、如图,把矩形沿对折后使两部分重合,若,则=(
)
A.110°
B.115°
C.120°
D.130°
3、如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.
70
B.
65
C.
60
D.
55
4、如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40°
B.
50°
C.
90°
D.
130°
5、将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.
30°
B.
45°
C.
60°
D.
65°
6、如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
A.
70°
B.
80°
C.
110°
D.
120°
7、如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=(
)
A.80°
B.
75°
C.
70°
D.
65°
8、如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=(
)
A.52°
B.38°
C.42°
D.60°
9、如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是
A.40°
B.60°
C.70°
D.80°
10、
如图,l∥m,∠1=115?,∠2=
95?,则∠3=(
)
A.120?
B.130?
C.140?
D.150?
11、如图,已知,,则的度数为(
)
(A)1150
(B)650
(C)600
(D)250
12、如图,已知∠1=700,如果CD∥BE,那么∠B的度数为
(
)
A.700
B.1000
C.1100
D.
1200
13、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
A.60°
B.65°
C.70°
D.
75°
14、已知:如图,AB∥CD,求证:∠B+∠D=∠BED。
15、已知:如图7,AB∥CD,求证:∠BED=∠D-∠B。
(二)
1、如图,已知
∠A=∠C,AB∥CD,请说明∠E=∠F的理由.
2、如图:已知
AB∥CD,∠EAB+∠FDC=180°,
求证:AE∥DF.
3、如图:∠1=∠2,
∠C=∠D.求证:∠A=∠F.
4、如图:已知,在△ABC中,∠ACB=900,AC=BC,D是AB的中点,AE=CF,
求证:DE⊥DF,DE=DF.
5、如图:已知在△ABC中,∠ACB=90°,∠BAC=30°,分别以AB,AC为边在△ABC外侧作等边三角形ABE和等边三角形ACD,DE与AB交于点F,
求证:EF=DF.
知识点四、多边形及其内角和
知识点:多边形的内角和定理
1.四边形内角和等于360°,能否利用三角形内角和等于180°得出结论:能
2.从上面的问题,你能想出五边形和六边形的内角和各是多少吗?观察图3,请填空:
(1)从五边形的一个顶点出发,可以引2条对角线,它们将五边形分为3个三角形,五边形的内角和等于180°×3.
(2)从六边形的一个顶点出发,可以引3条对角线,它们将六边形分为4个三角形,六边形的内角和等于180°×4.
3.一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引n-3条对角线,它们将n边形分为n-2个三角形,n边形的内角和等于180°×(n-2).
结论:多边形的内角和与边数的关系是
4.镶嵌的定义:用相状、大小完全一样的一种或几种平面图形进行拼接,彼此间不留空隙、不重叠得铺成一片,这就是平面图形的密铺,又称平面图形的镶嵌。
练一练
1、一个多边形的内角和是720°,这个多边形的边数是( )
A.4
B.5
C.6
D.7
2、一个多边形的内角和是900°,则这个多边形的边数为(
)
A.6
B.7
C.8
D.9
3、四边形的内角和为( )
A.180°
B.360°
C.540°
D.720°
4、正八边形的每个内角为(
)
A.120°
B.135°
C.140°
D.144°
5、正多边形的一个内角为135°,则该多边形的边数为( )
A.9
B.8
C.7
D.4
6、已知一个正多边形的一个内角是120°,则这个多边形的边是
.
7、五边形的外角和等于( )
A.180°
B.360°
C.540°
D.720°
一个正多边形,它的每一个外角都等于45°,则该正多边形是(
)
A.正六边形
B.正七边形
C.正八边形
D.正九边形
9、若一个正多边形的每个内角为150°,则这个正多边形的边数是(
)
A.12
B.11
C.10
D.9
10、已知一个多边形的内角和是外角和的3倍,则这个多边形为______边形.
11、若一个正多边形的一个外角为40?,则这个正多边形是_______边形.
12、如果一个多边形的内角和是其外角和的一半,那么这个多边
形是(
)
A.六边形
B.五边形
C.四边形
D.三角形
13、若凸边形的内角和为1260°,则从一个顶点出发引的对角线条数是_____________.
14、若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是(
)
A.十三边形
B.十二边形
C.十一边形
D.十边形
15、一个多边形的内角和为720°,那么这个多边形的对角线条数为(
)
A.6条
B.7条
C.8
D.9条
16、如图,依次以三角形、四边形、……、n边形的各顶点为圆心画半径为l的圆,且圆与圆之间两两不相交.把三角形与各圆重叠部分面积之和记为S3,四边形与各圆重叠部分面积之和记为S4,….n边形与各圆重叠部分面积之和记为Sn.则S90的值为_________________.(结果保留π)
17、如图,过正五边形ABCDE的顶点A作直线L∥CD,则∠1= .
18、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
19、现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有(
)
A.2种
B.3种
C.4种
D.5种
20、如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形
B.
正四边形
C.正六边形
D.正八边形
21、李刚同学设计了四种正多边形的瓷砖图案,在这四种瓷砖中,用一种瓷砖可以密铺平面的是( )
A.(1)(2)(4)
B.
(2)(3)(4)
C.(1)(3)(4)
D.(1)(2)(3)
课后作业
(一)
一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角
都等于140°,则它的边数是___________。
如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数
分别为_______。
若一个多边形的内角和为1080°,则它的边数是___________。
当一个多边形的边数增加1时,它的内角和增加_________度。
5.正十边形的一个外角为______.
6._______边形的内角和与外角和相等.
7.已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.【答案】十
已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形
B.五边形
C.六边形
D.七边形
9.一个正多边形,它的每一个外角都是45°,则该正多边形是( )
A.正六边形
B.正七边形
C.正八边形
D.正九边形
一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
11.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=
度.
、
一个多边形的每一个外角都等于24°,求这个多边形的边数.
13.如图,在五边形ABCDE中,AE⊥DE,∠BAE=120°,∠BCD=60°,∠CDE﹣∠ABC=30°.
(1)求∠D的度数;
(2)AB∥CD吗?请说明理由.
14.以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是 cm2.
如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有_______个。
(二)
1.下列语句是命题的有(
)
A.两点之间线段最短;
B.向雷锋同志学习;
C.对顶角相等;
D.花儿在春天开放;
E、对应角相等的两个三角形是全等三角形;
2.下列命题,哪些是真命题?哪些是假命题?如果是真命题,请写出条件与结论,如果是假命题,请举出反例.
A.同角的补角相等;B.同位角相等,两直线平行;C.若|a|=|b|,则a=b.
3.
如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
4.
用两个全等的等腰直角三角尺拼成四边形,则此四边形一定是_____。
5.
如图所示,△ABC中,∠ACD=115°,∠B=55°,
则∠A=
,
∠ACB=
6.
△ABC的三个外角度数比为3∶4∶5,则它的三个外角度数分别为
_____.
7.
已知,如图,AB∥CD,若∠ABE=130°,
∠CDE=152°,则∠
BED=__________.
第3题图
第5题图
第7题图
8、如图:已知AB=AD.BE=ED,
求证:①∠BAC=∠DAC
②BC=CD.
(三)
1.下列图形中,由,能得到的是(
)
2.如图,直线L1∥L2
,则∠α为(
).
A.1500
B.1400
C.1300
D.1200
3.下列命题:
①不相交的两条直线平行;
②梯形的两底互相平行;
③同垂直于一条直线的两直线平行;
④同旁内角相等,两直线平行.
其中真命题有(
)
A.1个
B.2个
C.3个
D.4个
4.下列命题:
①两个连续整数的乘积是偶数;②带有负号的数是负数;
③乘积是1的两个数互为倒数;④绝对值相等的两个数互为相反数.
其中假命题有(
)
A.1个
B.2个
C.3个
D.4个
5.如图,AB∥CD,那么∠BAE+∠AEC+∠ECD
=(
)
A.1800
B.2700
C.3600
D.5400
6.下列说法中,正确的是(
)
A.经过证明为正确的真命题叫公理
B.假命题不是命题
C.要证明一个命题是假命题,只要举一个反例,即举一个具备命题的条件,而不具备命题结论的命题即可
D.要证明一个命题是真命题,只要举一个例子,说明它正确即可.
7.下列选项中,真命题是(
).
A.a>b,a>c,则b=c
B.相等的角为对顶角
C.过直线l外一点,有且只有一条直线与直线l平行
D.三角形中至少有一个钝角
8.下列命题中,是假命题的是(
)
A.互补的两个角不能都是锐角
B.如果两个角相等,那么这两个角是对顶角
C.乘积为1的两个数互为倒数
D.全等三角形的对应角相等,对应边相等.
9.下列命题中,真命题是(
)
A.任何数的绝对值都是正数
B.任何数的零次幂都等于1
C.互为倒数的两个数的和为零
D.在数轴上表示的两个数,右边的数比左边的数大
10.如图所示,下列条件中,能判断AB∥CD的是(
)毛
A.∠BAD=∠BCD
B.∠1=∠2;
C.∠3=∠4
D.∠BAC=∠ACD
二、填空
11.观察如图所示的三棱柱.
(1)用符号表示下列线段的位置关系:
AC
CC1
,BC
B1C1
;
12.如图三角形ABC中,∠C
=
900
,AC=23,BC=32,把AC、BC、AB的大小关系用“>”号连接:
.
13.如图,直线AB、CD相交于点E
,DF∥AB,若∠AEC=1000,则∠D的度数等于
.
14.如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于
.
15.图中有
对对顶角.
三.用心解答(55)
16.如图,AB∥CD,AD∥BC,∠A﹦2∠B.求∠A、∠B、∠C、∠D的度数.
17.如图,AB∥CD,直线EF交AB、CD于点G、H.如果GM平分∠BGF,HN平分∠CHE,那么,GM与HN平行吗?为什么?
18.如图,AB∥CD,∠BAE=300,∠ECD=600,那么∠AEC度数为多少?
19.如图,B处在A处的南偏西450方向,C处在B处的北偏东800方向.(1)求∠ABC.(2)要使CD∥AB,D处应在C处的什么方向?(12分)
20、如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
(13分)
学生姓名
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
平行线
教学目标
1、理解平行线的概念;掌握多边形的内角和公式以及多边形外角和公式。
2、掌握平行线的公理及其推论;理解内角和定理的推导。
3、能熟练掌握平行线的应用。
教学重点与难点
重点:理解平行线的概念;掌握多边形的内角和公式以及多边形外角和公式。
难点:掌握平行线的公理及其推论;理解内角和定理的推导。
知识点一、定义与命题
1、命题含义(情景引入)
活动内容:
如果B处水流受到污染,那么____处水流便受到污染;
如果C处水流受到污染,那么____处水流便受到污染;
如果D处水流受到污染,那么____处水流便受到污染;
如果____处水流受到污染,那么____处水流便受到污染.
在假设的前提条件下,对某一处受到污染作出了判断,像这样,对事情作出判断的句子,就叫做命题.
命题的定义:命题是判断一件事情的句子.
如:熊猫没有翅膀.对顶角相等.
举例
两直线平行,内错角相等.
无论n为任意的自然数,式子n2-n+11的值都是质数.
内错角相等.
任意一个三角形都有一个直角.
如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
全等三角形的对应角相等.
……
注意:
你喜欢数学吗?
作线段AB=a.
平行用符号“∥”表示.
这些句子没有对某一件事情作出任何判断,那么它们就不是命题.
一般情况下:疑问句不是命题.图形的作法不是命题.)
2、探讨
①
探讨命题的结构特征
观察下列命题,发现它们的结构有什么共同特征?
(1)如果两个三角形的三条边对应相等,那么这两个三角形全等.
(2)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
(3)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形.
(4)如果一个四边的对角线相等,那么这个四边形是矩形.
(5)如果一个四边形的两条对角线互相垂直,那么这个四边形是菱形.
②
总结命题的结构特征
(1)上述命题都是“如果……,那么……”的形式.
(2)“如果……”是已知的事项,“那么……”是由已知事项推断出的结论.
(3)一般地命题都可以写成“如果……,那么……”的形式,其中“如果”引出的部分是条件,“那么”引出的结论,每个命题都有条件和结论.
3、定义与命题
①
定义的含义:对名称和术语的含义加以描述,作出明确的规定,就是它们的定义;
②
命题的含义:判断一件事情的句子,叫做命题,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
知识点二、相交线
1、相交线
在同一平面内,两条直线的位置关系有平行和相交。
(2)相交:在同一平面内,有一个公共点的两条直线称为相交线。
(3)邻补角与对顶角
定义:有公共顶点,且有一条公共边,另一条边互为反向延长线,具有这种位置关系的两个角,互为邻补角。邻补角互补。
定义:有一个公共顶点,并且有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角。对顶角相等。
两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:
图形顶点边的关系大小关系对顶角
∠1与∠2有公共顶点∠1的两边与∠2的两边互为反向延长线对顶角相等
即∠1=∠2邻补角
∠3与∠4
有公共顶点∠3与∠4有一条边公共,另一边互为反向延长线。∠3+∠4=180°
注意:(1)对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;
(2)如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角
(3)如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2.垂线
定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:
如图所示:AB⊥CD,垂足为O
垂线性质1:过一点有且只有一条直线与已知直线垂直。
垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。简称:垂线段最短。
3.垂线的画法:
过直线上一点画已知直线的垂线;
过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;
②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:一靠:用三角尺一条直角边靠在已知直线上;
二移:移动三角尺使一点落在它的另一边直角边上;
三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4.点到直线的距离
(1)定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的________.
如图,PO⊥AB,点P到直线AB的距离是PO的长。PO是垂线段。
PO是点P到直线AB所有线段中最短的一条。
(2)应用:现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
5.“垂线”、“垂线段”、“两点间距离”、“点到直线
的距离”联系与区别
垂线与垂线段的区别:区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。
联系:具有垂直于已知直线的共同特征。(垂直的性质)
两点间距离与点到直线的距离
区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。
联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
线段与距离
距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
三线八角
两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角。
如图,直线被直线所截
(1)∠1与∠5在截线的同侧,同在被截直线的上方,
叫做__________(位置相同)
(2)∠5与∠3在截线的两旁(交错),在被截直线之间(内),叫做_________(位置在内且交错)
(3)∠5与∠4在截线的同侧,在被截直线之间(内),叫做____________。
(4)三线八角也可以成模型中看出。同位角是“A”型;内错角是“Z”型;同旁内角是“U”型。
知识点三、平行线
1.平行线的概念
在同一个平面内,不相交的两条直线叫做平行线。平行用符号“∥”表示,如“AB∥CD”,读作“AB平行于CD”。
同一平面内,两条直线的位置关系只有两种:平行或相交。
注意:
(1)平行线是无限延伸的,无论怎样延伸也不相交。
(2)当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
2.平行线公理及其推论
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
3.平行线的性质
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
练一练
1、如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为
.
2、如图,把矩形沿对折后使两部分重合,若,则=(
)
A.110°
B.115°
C.120°
D.130°
3、如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
A.
70
B.
65
C.
60
D.
55
4、如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40°
B.
50°
C.
90°
D.
130°
5、将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.
30°
B.
45°
C.
60°
D.
65°
6、如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
A.
70°
B.
80°
C.
110°
D.
120°
7、如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=(
)
A.80°
B.
75°
C.
70°
D.
65°
8、如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=(
)
A.52°
B.38°
C.42°
D.60°
9、如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是
A.40°
B.60°
C.70°
D.80°
10、
如图,l∥m,∠1=115?,∠2=
95?,则∠3=(
)
A.120?
B.130?
C.140?
D.150?
11、如图,已知,,则的度数为(
)
(A)1150
(B)650
(C)600
(D)250
12、如图,已知∠1=700,如果CD∥BE,那么∠B的度数为
(
)
A.700
B.1000
C.1100
D.
1200
13、如图,在△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
A.60°
B.65°
C.70°
D.
75°
14、已知:如图,AB∥CD,求证:∠B+∠D=∠BED。
15、已知:如图7,AB∥CD,求证:∠BED=∠D-∠B。
(二)
1、如图,已知
∠A=∠C,AB∥CD,请说明∠E=∠F的理由.
2、如图:已知
AB∥CD,∠EAB+∠FDC=180°,
求证:AE∥DF.
3、如图:∠1=∠2,
∠C=∠D.求证:∠A=∠F.
4、如图:已知,在△ABC中,∠ACB=900,AC=BC,D是AB的中点,AE=CF,
求证:DE⊥DF,DE=DF.
5、如图:已知在△ABC中,∠ACB=90°,∠BAC=30°,分别以AB,AC为边在△ABC外侧作等边三角形ABE和等边三角形ACD,DE与AB交于点F,
求证:EF=DF.
知识点四、多边形及其内角和
知识点:多边形的内角和定理
1.四边形内角和等于360°,能否利用三角形内角和等于180°得出结论:能
2.从上面的问题,你能想出五边形和六边形的内角和各是多少吗?观察图3,请填空:
(1)从五边形的一个顶点出发,可以引2条对角线,它们将五边形分为3个三角形,五边形的内角和等于180°×3.
(2)从六边形的一个顶点出发,可以引3条对角线,它们将六边形分为4个三角形,六边形的内角和等于180°×4.
3.一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引n-3条对角线,它们将n边形分为n-2个三角形,n边形的内角和等于180°×(n-2).
结论:多边形的内角和与边数的关系是
4.镶嵌的定义:用相状、大小完全一样的一种或几种平面图形进行拼接,彼此间不留空隙、不重叠得铺成一片,这就是平面图形的密铺,又称平面图形的镶嵌。
练一练
1、一个多边形的内角和是720°,这个多边形的边数是( )
A.4
B.5
C.6
D.7
2、一个多边形的内角和是900°,则这个多边形的边数为(
)
A.6
B.7
C.8
D.9
3、四边形的内角和为( )
A.180°
B.360°
C.540°
D.720°
4、正八边形的每个内角为(
)
A.120°
B.135°
C.140°
D.144°
5、正多边形的一个内角为135°,则该多边形的边数为( )
A.9
B.8
C.7
D.4
6、已知一个正多边形的一个内角是120°,则这个多边形的边是
.
7、五边形的外角和等于( )
A.180°
B.360°
C.540°
D.720°
一个正多边形,它的每一个外角都等于45°,则该正多边形是(
)
A.正六边形
B.正七边形
C.正八边形
D.正九边形
9、若一个正多边形的每个内角为150°,则这个正多边形的边数是(
)
A.12
B.11
C.10
D.9
10、已知一个多边形的内角和是外角和的3倍,则这个多边形为______边形.
11、若一个正多边形的一个外角为40?,则这个正多边形是_______边形.
12、如果一个多边形的内角和是其外角和的一半,那么这个多边
形是(
)
A.六边形
B.五边形
C.四边形
D.三角形
13、若凸边形的内角和为1260°,则从一个顶点出发引的对角线条数是_____________.
14、若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是(
)
A.十三边形
B.十二边形
C.十一边形
D.十边形
15、一个多边形的内角和为720°,那么这个多边形的对角线条数为(
)
A.6条
B.7条
C.8
D.9条
16、如图,依次以三角形、四边形、……、n边形的各顶点为圆心画半径为l的圆,且圆与圆之间两两不相交.把三角形与各圆重叠部分面积之和记为S3,四边形与各圆重叠部分面积之和记为S4,….n边形与各圆重叠部分面积之和记为Sn.则S90的值为_________________.(结果保留π)
17、如图,过正五边形ABCDE的顶点A作直线L∥CD,则∠1= .
18、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
19、现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有(
)
A.2种
B.3种
C.4种
D.5种
20、如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A.正三角形
B.
正四边形
C.正六边形
D.正八边形
21、李刚同学设计了四种正多边形的瓷砖图案,在这四种瓷砖中,用一种瓷砖可以密铺平面的是( )
A.(1)(2)(4)
B.
(2)(3)(4)
C.(1)(3)(4)
D.(1)(2)(3)
课后作业
(一)
一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角
都等于140°,则它的边数是___________。
如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数
分别为_______。
若一个多边形的内角和为1080°,则它的边数是___________。
当一个多边形的边数增加1时,它的内角和增加_________度。
5.正十边形的一个外角为______.
6._______边形的内角和与外角和相等.
7.已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.【答案】十
已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形
B.五边形
C.六边形
D.七边形
9.一个正多边形,它的每一个外角都是45°,则该正多边形是( )
A.正六边形
B.正七边形
C.正八边形
D.正九边形
一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
11.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=
度.
、
一个多边形的每一个外角都等于24°,求这个多边形的边数.
13.如图,在五边形ABCDE中,AE⊥DE,∠BAE=120°,∠BCD=60°,∠CDE﹣∠ABC=30°.
(1)求∠D的度数;
(2)AB∥CD吗?请说明理由.
14.以四边形ABCD各个顶点为圆心,1cm长为半径画弧,则图中阴影部分面积之和是 cm2.
如图,是由12个边长相等的正三角形镶嵌而成的平面图形,则图中的平行四边形共有_______个。
(二)
1.下列语句是命题的有(
)
A.两点之间线段最短;
B.向雷锋同志学习;
C.对顶角相等;
D.花儿在春天开放;
E、对应角相等的两个三角形是全等三角形;
2.下列命题,哪些是真命题?哪些是假命题?如果是真命题,请写出条件与结论,如果是假命题,请举出反例.
A.同角的补角相等;B.同位角相等,两直线平行;C.若|a|=|b|,则a=b.
3.
如图,AD、BE、CF为△ABC的三条角平分线,则:∠1+∠2+∠3=________.
4.
用两个全等的等腰直角三角尺拼成四边形,则此四边形一定是_____。
5.
如图所示,△ABC中,∠ACD=115°,∠B=55°,
则∠A=
,
∠ACB=
6.
△ABC的三个外角度数比为3∶4∶5,则它的三个外角度数分别为
_____.
7.
已知,如图,AB∥CD,若∠ABE=130°,
∠CDE=152°,则∠
BED=__________.
第3题图
第5题图
第7题图
8、如图:已知AB=AD.BE=ED,
求证:①∠BAC=∠DAC
②BC=CD.
(三)
1.下列图形中,由,能得到的是(
)
2.如图,直线L1∥L2
,则∠α为(
).
A.1500
B.1400
C.1300
D.1200
3.下列命题:
①不相交的两条直线平行;
②梯形的两底互相平行;
③同垂直于一条直线的两直线平行;
④同旁内角相等,两直线平行.
其中真命题有(
)
A.1个
B.2个
C.3个
D.4个
4.下列命题:
①两个连续整数的乘积是偶数;②带有负号的数是负数;
③乘积是1的两个数互为倒数;④绝对值相等的两个数互为相反数.
其中假命题有(
)
A.1个
B.2个
C.3个
D.4个
5.如图,AB∥CD,那么∠BAE+∠AEC+∠ECD
=(
)
A.1800
B.2700
C.3600
D.5400
6.下列说法中,正确的是(
)
A.经过证明为正确的真命题叫公理
B.假命题不是命题
C.要证明一个命题是假命题,只要举一个反例,即举一个具备命题的条件,而不具备命题结论的命题即可
D.要证明一个命题是真命题,只要举一个例子,说明它正确即可.
7.下列选项中,真命题是(
).
A.a>b,a>c,则b=c
B.相等的角为对顶角
C.过直线l外一点,有且只有一条直线与直线l平行
D.三角形中至少有一个钝角
8.下列命题中,是假命题的是(
)
A.互补的两个角不能都是锐角
B.如果两个角相等,那么这两个角是对顶角
C.乘积为1的两个数互为倒数
D.全等三角形的对应角相等,对应边相等.
9.下列命题中,真命题是(
)
A.任何数的绝对值都是正数
B.任何数的零次幂都等于1
C.互为倒数的两个数的和为零
D.在数轴上表示的两个数,右边的数比左边的数大
10.如图所示,下列条件中,能判断AB∥CD的是(
)毛
A.∠BAD=∠BCD
B.∠1=∠2;
C.∠3=∠4
D.∠BAC=∠ACD
二、填空
11.观察如图所示的三棱柱.
(1)用符号表示下列线段的位置关系:
AC
CC1
,BC
B1C1
;
12.如图三角形ABC中,∠C
=
900
,AC=23,BC=32,把AC、BC、AB的大小关系用“>”号连接:
.
13.如图,直线AB、CD相交于点E
,DF∥AB,若∠AEC=1000,则∠D的度数等于
.
14.如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于
.
15.图中有
对对顶角.
三.用心解答(55)
16.如图,AB∥CD,AD∥BC,∠A﹦2∠B.求∠A、∠B、∠C、∠D的度数.
17.如图,AB∥CD,直线EF交AB、CD于点G、H.如果GM平分∠BGF,HN平分∠CHE,那么,GM与HN平行吗?为什么?
18.如图,AB∥CD,∠BAE=300,∠ECD=600,那么∠AEC度数为多少?
19.如图,B处在A处的南偏西450方向,C处在B处的北偏东800方向.(1)求∠ABC.(2)要使CD∥AB,D处应在C处的什么方向?(12分)
20、如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
(13分)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
