北师大版九年级上册第四章 图形的相似(一)学案(表格式)
文档属性
| 名称 | 北师大版九年级上册第四章 图形的相似(一)学案(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 243.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 19:56:03 | ||
图片预览




文档简介
图形的相似(1)
学生姓名
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
图形的相似(一)
教学目标
1、理解比例成比例线段,平行线分线段成比例定理。
2、理解相似图形、相似多边形和相似比的概念。
3、掌握相似多边形的两个基本性质。
4、了解位似图象和位似中心的概念,能用位似的性质将一个图形放大或缩小;
5、经历图形的位似变换与平移、旋转的过程,体会图形间的变换过程以及内在的联系
6、了解三角形相似的条件和判定定理。
教学重点与难点
重点:例成比例线段,平行线分线段成比例定理
难点:相似多边形的两个基本性质
一、作业检查
作业完成情况:优
良
中
差
内容回顾
回顾上节课内容
知识整理
知识点一、两条线段的比
1、两条线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是它们长度的比,即AB:CD=m:n,或写成.
【例1】如图,设小方格的边长是1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD,EH,EF的长度分别是多少?分别计算的值,你发现了什么?
练1.
一条线段的长度是另一条线段的5倍,求这两条线段的比.
2、比例线段
对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等(如),那么称这四条线段是成比例线段,简称比例线段.
【例题】如图,一块矩形绸布的长AB=
a
m,宽AD=1m,按照图中所表示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是多少?
总结:
如果,那么.
如果(a,b,c,d都不等于0),那么.
练1.在△ABC中,∠B=90°,AB=BC=10cm;在△DEF中,
ED=EF=12cm,DF=8cm,求AB与EF之比,AC与DF之比.
练2.如图,在△ABC中,
AB=
12cm,
AE=6cm,EC=5cm,且,求AD的长.
3.
比例性质
如果,那么
【例3】在△ABC与△DEF中,已知,且△ABC的周长为18cm.
求△DEF的周长.
练1.
已知,求的值.
练2.如图,已知每个小方格的边长均为1,求AB,DE,BC,DC,AC,EC的长,并计算△ABC与△EDC的周长比.
4.平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成比例.
平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
【例】如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
练1.已知两条直线被三条平行线所截,截得线段的长度如图,求
的值.
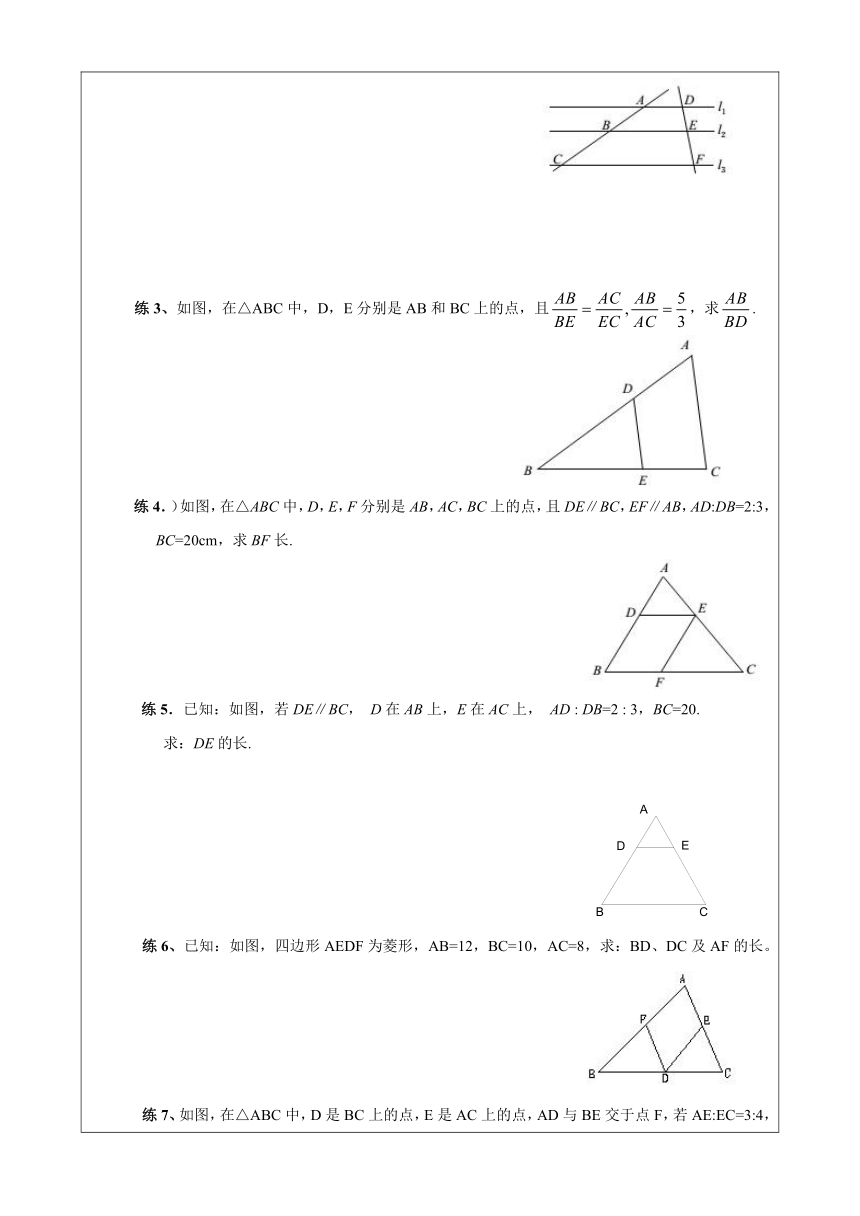
练2.如图,已知l1∥l2∥l3.
AB=5,BC=7,EF=4,求DE的长.
练3、如图,在△ABC中,D,E分别是AB和BC上的点,且,求.
练4.)如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,
BC=20cm,求BF长.
练5.已知:如图,若DE∥BC,
D在AB上,E在AC上,
AD
:
DB=2
:
3,BC=20.
求:DE的长.
练6、已知:如图,四边形AEDF为菱形,AB=12,BC=10,AC=8,求:BD、DC及AF的长。
练7、如图,在△ABC中,D是BC上的点,E是AC上的点,AD与BE交于点F,若AE:EC=3:4,
BD:DC=2:3,求BF:EF的值.
练8.如图,DE∥AB,EF∥BC,AF=5cm,
FB=3cm,
CD=2cm,求
BD.
知识点二、相似图形
1.相似图形
形状相同的图形是相似图形.
2.相似多边形
相似多边形对应角相等,对应边的比相等.
反过来,如果两个多边形满足对应角相等
,对应边的比相等那么这两个多边形相似.我们把相似多边形对应边的比成为
相似比.
【练习】
【例1】如图,图形a~f中,哪些是与图形(1)或(2)相似的?
练1.
观察下列图形,指出哪些是相似图形:
练2、下图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?
练3.下列说法正确的是(
)
A.所有的平行四边形都相似
B.所有的矩形都相似
C.所有的菱形都相似
D.所有的正方形都相似
练4.在一张比例尺为1∶20000的地图上,量得A与B两地的距离是5cm,则A,B两地实际距离为______m.
练5.
已知四边形ABCD与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长.
练6、△ABC与△DEF相似,且相似比是,则△DEF
与△ABC与的相似比是(
).
A.
B.
C.
D.
总结:
面积比等于相似比的平方.
练7.已知2a-3b=0,b≠0,则a∶b=______.
练8.若则______..
练9、要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有(
)
A.1种
B.2种
C.3种
D.4种
练10.下列所给的条件中,能确定相似的有(
)
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个
B.4个
C.5个
D.6个
练11.下列图形一定是相似图形的是(
)
A.任意两个菱形
B.任意两个正三角形
C.两个等腰三角形
D.两个矩形
练12、已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
练13.已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?
练14.如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EFAB相似,求EF的长.
练15.已知:如图,△ABC中,AB=20,BC=14,AC=12.△ADE与△ACB相似,∠AED=∠B,DE=5.求AD,AE的长.
课堂检测
1.已知3x=5y
,则x:y=_________;
2.已知x:y=7:2,求x:(x+y)________.
3..如图,若EF∥AB,
DE∥AC,
以下比例正确的有(
)个.
A.
1个.
B.
2个.
C.
3个.
D.
4个.
4.如图,已知DC//EF//GH//AB,AB=30,CD=6,且DE:EG:GA=1:2:3,则EF=______GH=
______.
5.在下面的图形中,形状相似的一组是(
)
6.如图所示,AB∥CD,AE∥FD,AE,FD分别交BC于点G,H,则图中共有相似三角形(
).
A.4对
B.5对
C.6对
D.7对
7.如图所示,在梯形ABCD中,AB∥CD,中位线EF交对角线AC,BD于M,N两点,若EF=18cm,MN=8cm,则AB的长是___________.
8.灯P在横杆AB的正上方,AB在灯光下的影长为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则点P到AB的距离是(
).
A.
9.
如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=,则此三角形移动的距离PP′是(
).
A.
B.
C.1
D.-1
学生姓名
年级
学科
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:
3
课时
教学课题
图形的相似(一)
教学目标
1、理解比例成比例线段,平行线分线段成比例定理。
2、理解相似图形、相似多边形和相似比的概念。
3、掌握相似多边形的两个基本性质。
4、了解位似图象和位似中心的概念,能用位似的性质将一个图形放大或缩小;
5、经历图形的位似变换与平移、旋转的过程,体会图形间的变换过程以及内在的联系
6、了解三角形相似的条件和判定定理。
教学重点与难点
重点:例成比例线段,平行线分线段成比例定理
难点:相似多边形的两个基本性质
一、作业检查
作业完成情况:优
良
中
差
内容回顾
回顾上节课内容
知识整理
知识点一、两条线段的比
1、两条线段的比
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m,n,那么这两条线段的比就是它们长度的比,即AB:CD=m:n,或写成.
【例1】如图,设小方格的边长是1,四边形ABCD与四边形EFGH的顶点都在格点上,那么AB,AD,EH,EF的长度分别是多少?分别计算的值,你发现了什么?
练1.
一条线段的长度是另一条线段的5倍,求这两条线段的比.
2、比例线段
对于四条线段a,b,c,d,如果其中两条线段的比与另两条线段的比相等(如),那么称这四条线段是成比例线段,简称比例线段.
【例题】如图,一块矩形绸布的长AB=
a
m,宽AD=1m,按照图中所表示的方式将它裁成相同的三面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是多少?
总结:
如果,那么.
如果(a,b,c,d都不等于0),那么.
练1.在△ABC中,∠B=90°,AB=BC=10cm;在△DEF中,
ED=EF=12cm,DF=8cm,求AB与EF之比,AC与DF之比.
练2.如图,在△ABC中,
AB=
12cm,
AE=6cm,EC=5cm,且,求AD的长.
3.
比例性质
如果,那么
【例3】在△ABC与△DEF中,已知,且△ABC的周长为18cm.
求△DEF的周长.
练1.
已知,求的值.
练2.如图,已知每个小方格的边长均为1,求AB,DE,BC,DC,AC,EC的长,并计算△ABC与△EDC的周长比.
4.平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成比例.
平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
【例】如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
练1.已知两条直线被三条平行线所截,截得线段的长度如图,求
的值.
练2.如图,已知l1∥l2∥l3.
AB=5,BC=7,EF=4,求DE的长.
练3、如图,在△ABC中,D,E分别是AB和BC上的点,且,求.
练4.)如图,在△ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=2:3,
BC=20cm,求BF长.
练5.已知:如图,若DE∥BC,
D在AB上,E在AC上,
AD
:
DB=2
:
3,BC=20.
求:DE的长.
练6、已知:如图,四边形AEDF为菱形,AB=12,BC=10,AC=8,求:BD、DC及AF的长。
练7、如图,在△ABC中,D是BC上的点,E是AC上的点,AD与BE交于点F,若AE:EC=3:4,
BD:DC=2:3,求BF:EF的值.
练8.如图,DE∥AB,EF∥BC,AF=5cm,
FB=3cm,
CD=2cm,求
BD.
知识点二、相似图形
1.相似图形
形状相同的图形是相似图形.
2.相似多边形
相似多边形对应角相等,对应边的比相等.
反过来,如果两个多边形满足对应角相等
,对应边的比相等那么这两个多边形相似.我们把相似多边形对应边的比成为
相似比.
【练习】
【例1】如图,图形a~f中,哪些是与图形(1)或(2)相似的?
练1.
观察下列图形,指出哪些是相似图形:
练2、下图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?
练3.下列说法正确的是(
)
A.所有的平行四边形都相似
B.所有的矩形都相似
C.所有的菱形都相似
D.所有的正方形都相似
练4.在一张比例尺为1∶20000的地图上,量得A与B两地的距离是5cm,则A,B两地实际距离为______m.
练5.
已知四边形ABCD与四边形A1B1C1D1相似,且A1B1:B1C1:C1D1:D1A1=7:8:11:14,若四边形ABCD的周长为40,求四边形ABCD的各边的长.
练6、△ABC与△DEF相似,且相似比是,则△DEF
与△ABC与的相似比是(
).
A.
B.
C.
D.
总结:
面积比等于相似比的平方.
练7.已知2a-3b=0,b≠0,则a∶b=______.
练8.若则______..
练9、要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm,60cm,80cm,三角形框架乙的一边长为20cm,那么,符合条件的三角形框架乙共有(
)
A.1种
B.2种
C.3种
D.4种
练10.下列所给的条件中,能确定相似的有(
)
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个
B.4个
C.5个
D.6个
练11.下列图形一定是相似图形的是(
)
A.任意两个菱形
B.任意两个正三角形
C.两个等腰三角形
D.两个矩形
练12、已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
练13.已知四边形ABCD和四边形A1B1C1D1相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形A1B1C1D1的最短边的长是6cm,那么四边形A1B1C1D1中最长的边长是多少?
练14.如图,AB∥EF∥CD,CD=4,AB=9,若梯形CDEF与梯形EFAB相似,求EF的长.
练15.已知:如图,△ABC中,AB=20,BC=14,AC=12.△ADE与△ACB相似,∠AED=∠B,DE=5.求AD,AE的长.
课堂检测
1.已知3x=5y
,则x:y=_________;
2.已知x:y=7:2,求x:(x+y)________.
3..如图,若EF∥AB,
DE∥AC,
以下比例正确的有(
)个.
A.
1个.
B.
2个.
C.
3个.
D.
4个.
4.如图,已知DC//EF//GH//AB,AB=30,CD=6,且DE:EG:GA=1:2:3,则EF=______GH=
______.
5.在下面的图形中,形状相似的一组是(
)
6.如图所示,AB∥CD,AE∥FD,AE,FD分别交BC于点G,H,则图中共有相似三角形(
).
A.4对
B.5对
C.6对
D.7对
7.如图所示,在梯形ABCD中,AB∥CD,中位线EF交对角线AC,BD于M,N两点,若EF=18cm,MN=8cm,则AB的长是___________.
8.灯P在横杆AB的正上方,AB在灯光下的影长为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则点P到AB的距离是(
).
A.
9.
如图,把△PQR沿着PQ的方向平移到△P′Q′R′的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=,则此三角形移动的距离PP′是(
).
A.
B.
C.1
D.-1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
