北师大版九年级上册第一章 特殊平行四边形学案(表格式)
文档属性
| 名称 | 北师大版九年级上册第一章 特殊平行四边形学案(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 19:57:47 | ||
图片预览

文档简介
特殊平行四边形
学生姓名
性别
年级
初三
学科
数学
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:3课时
教学课题
特殊的平行四边形
教学目标
1、理解菱形、矩形、正方形的定义、性质
2、能运用判定方法来证明。
3、会用菱形、矩形、正方形的性质解决简单的证明和计算问题;
教学重点与难点
重点:.矩形、正方形的性质、判定以及判定的应用
难点:相关知识的综合应用
一.
作业检查
作业完成情况:优□
良□
中□
差□
二.
内容回顾
回顾上节课内容.
知识梳理
知识点一、菱形
1.菱形的性质
(1)菱形的定义:
有一组邻边相等的平行四边形叫做菱形.(平行四边形+一组邻边相等=菱形)
(2)菱形的性质:
菱形具有平行四边形的一切性质;
A、边:对边平行且相等
B、角:菱形的对角相等,邻角互补
C、对角线:两条对角线互相平分且垂直
每一条对角线平分一组对角
D、对称性:中心对称:对角线的交点就是对称中心
轴对称:有两条对称轴。即:两条对角线所在的直线
(3)菱形的面积计算
①利用平行四边形的面积公式.
②菱形面积=1/2ab.(a、b是两条对角线的长度)
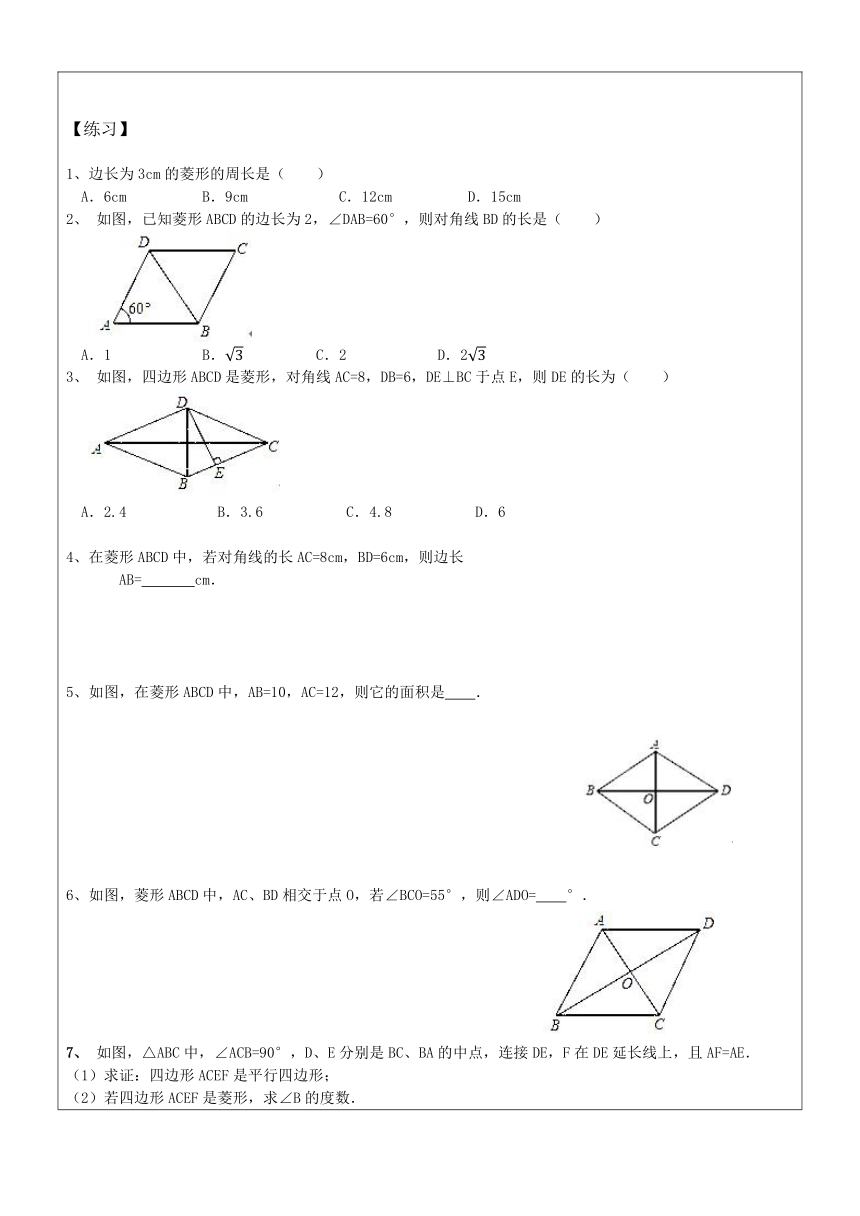
【练习】
1、边长为3cm的菱形的周长是( )
A.6cm
B.9cm
C.12cm
D.15cm
2、
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1
B.
C.2
D.2
3、
如图,四边形ABCD是菱形,对角线AC=8,DB=6,DE⊥BC于点E,则DE的长为( )
A.2.4
B.3.6
C.4.8
D.6
4、在菱形ABCD中,若对角线的长AC=8cm,BD=6cm,则边长
AB=
cm.
如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 .
6、如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO= °.
7、
如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
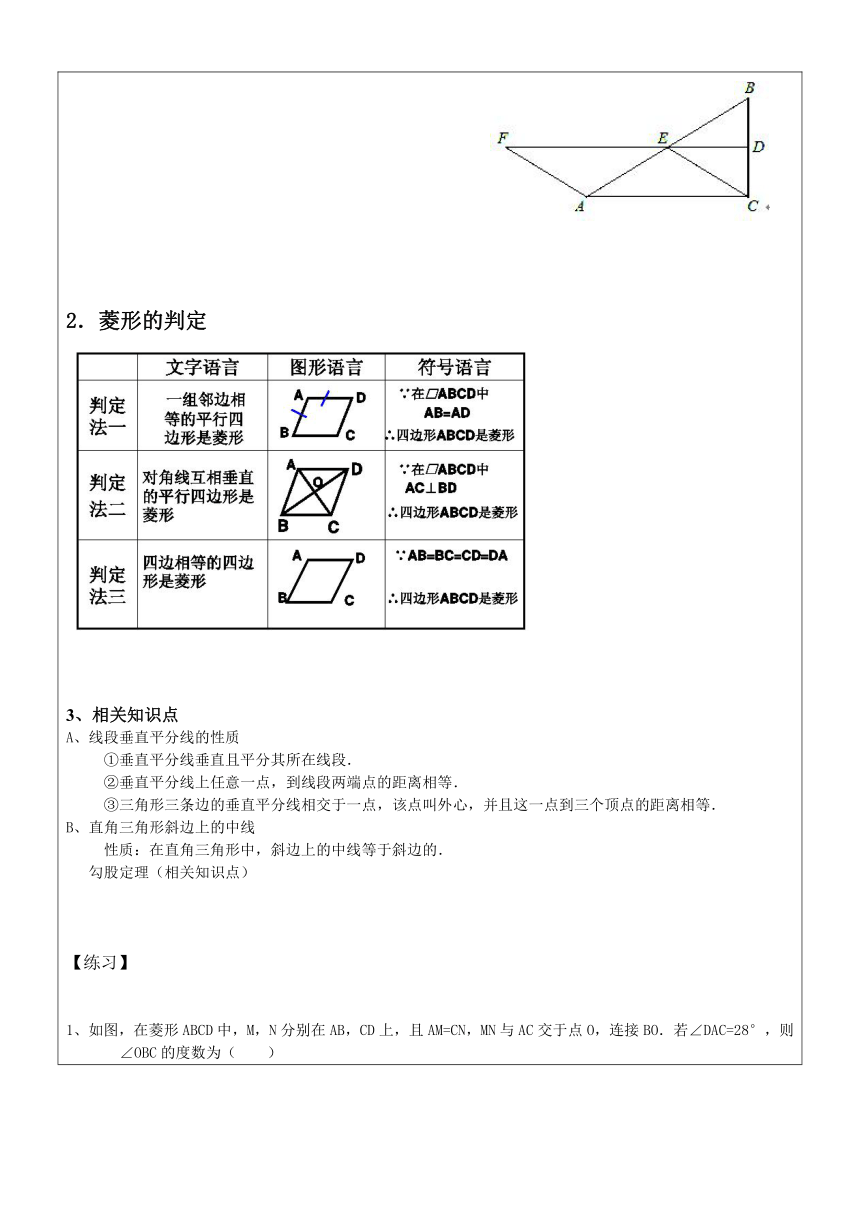
菱形的判定
3、相关知识点
A、线段垂直平分线的性质
①垂直平分线垂直且平分其所在线段.
②垂直平分线上任意一点,到线段两端点的距离相等.
③三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.
B、直角三角形斜边上的中线
性质:在直角三角形中,斜边上的中线等于斜边的.
勾股定理(相关知识点)
【练习】
1、如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28°
B.52°
C.62°
D.72°
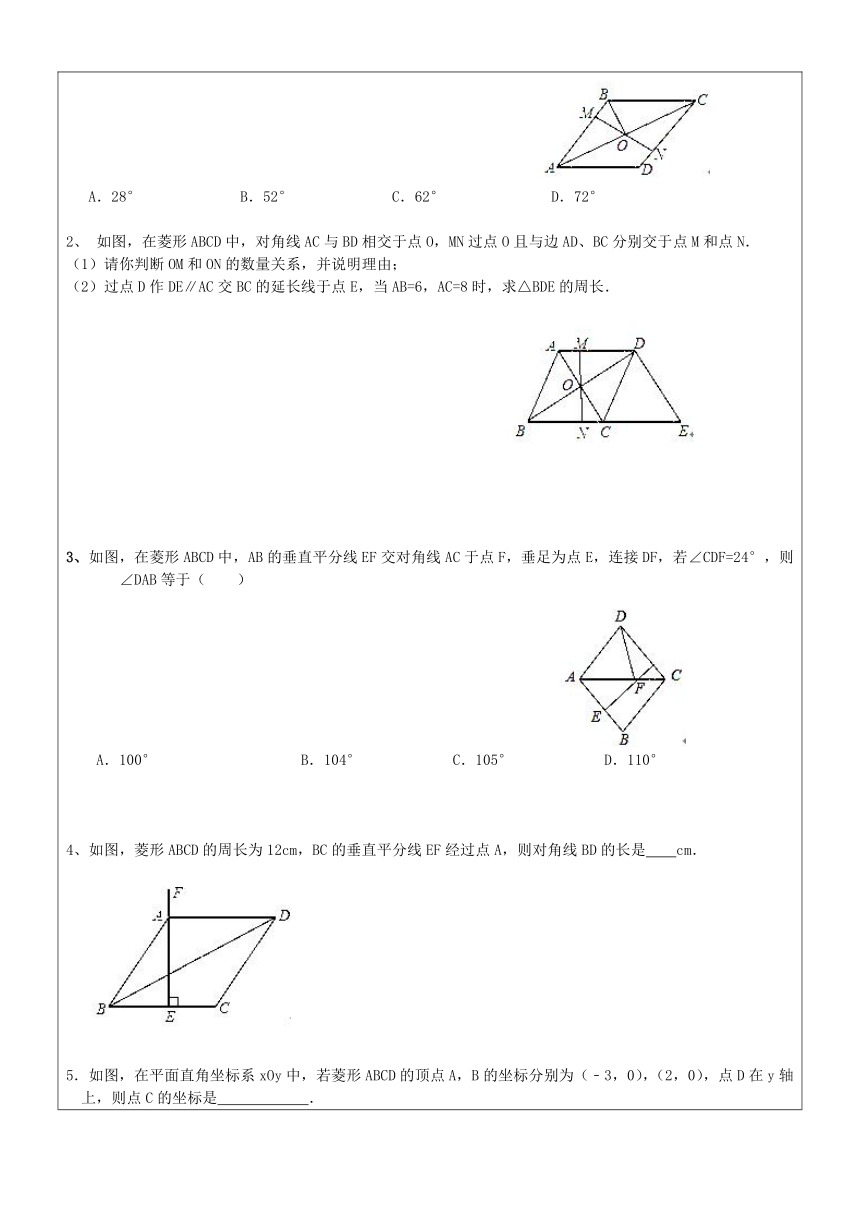
2、
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
3、如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
A.100°
B.104°
C.105°
D.110°
如图,菱形ABCD的周长为12cm,BC的垂直平分线EF经过点A,则对角线BD的长是 cm.
5.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是 .
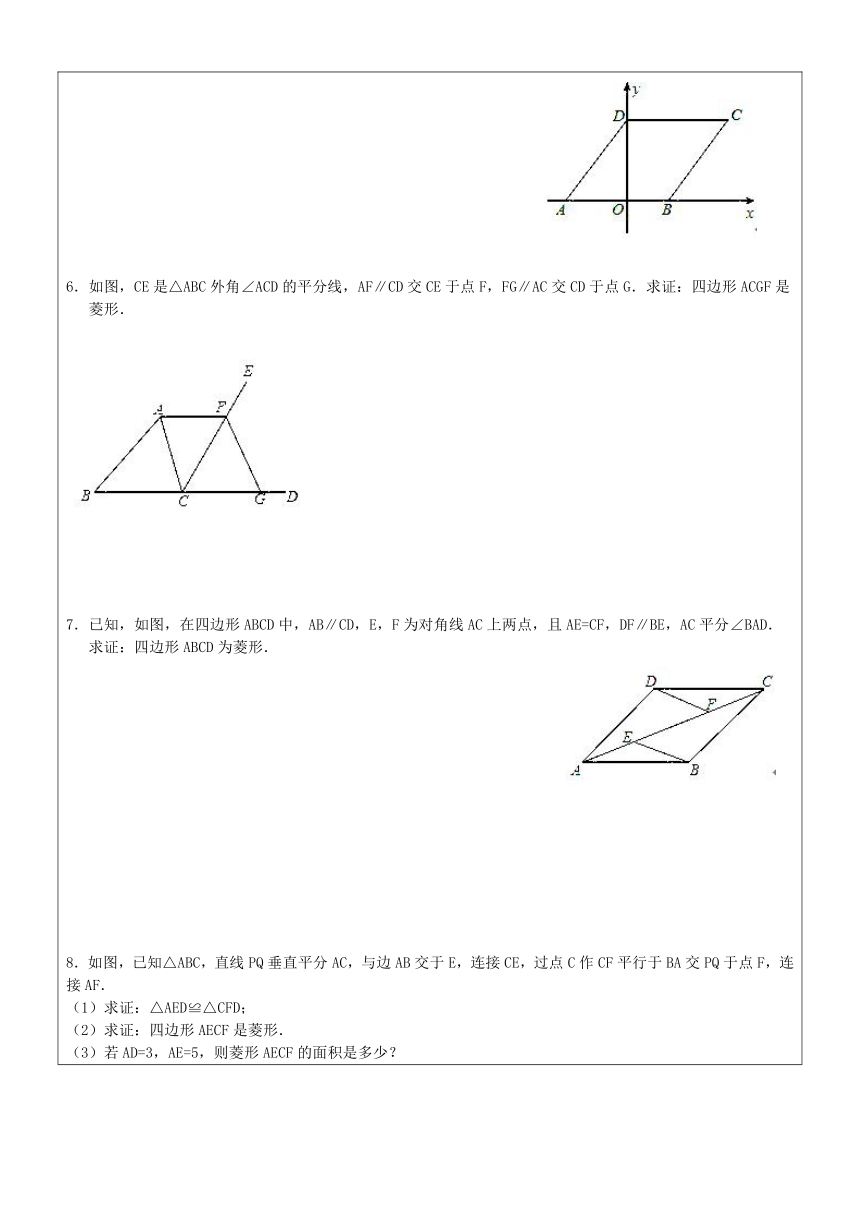
6.如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
7.已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
求证:四边形ABCD为菱形.
8.如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
9、已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
10、已知:如图四边形ABCD的对角线AC的垂直平分线与边AD,
BC分别交于E,
F.求证:四边形AFCE是菱形.
11、已知如图,菱形ABCD中,E是BC上一点,AE,
BD交于M,若AB=AE,∠EAD=2∠BAE.求证:AM=BE.
12、如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.求线段BE的长.
13、如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F.请你猜想DE与DF的大小有什么关系?并证明你的猜想
12、如图,菱形ABCD的边长为2,BD=2,E,
F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
知识点二、矩形
1.
矩形的定义:有一个角是直角的平行四边形是矩形。
2.
矩形的性质:A、边:对边平行且相等
B、四个角都是直角
C、对角线相等且平分
3、拓展:
直角三角形性质定理:直角三角形斜边上的中线等于斜边的一半。
练习:
1、如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为( )
A.30°
B.60°
C.90°
D.120°
2、如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90°
B.AC=BD
C.OA=OB
D.OA=AD
3、
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
5、如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是 .
6、
若平行四边形的两条对角线长为6
cm和16
cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm
B.8cm
C.12cm
D.16cm
7、如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm
B.4cm
C.2cm
D.1cm
8、如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( )
A.1
B.2
C.3
D.4
矩形的判定
角:
判定一:有三个角是直角的四边形是矩形。
判定二:有一个角是直角的平行四边形是矩形。
对角线:
判定三:对角线相等的平行四边形是矩形。
判定四:对角线相互平分且相等的四边形是矩形。
1、如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
2、
已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论:P
A2+PC2=PB2+PD2,请你探究:当点P分别在图(2)、图(3)中的位置时,PA2、PB2、PC2和PD2又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.
答:对图(2)的探究结论为 ;
对图(3)的探究结论为 ;
3、如图,AB=CD=ED,AD=EB,BE⊥DE,垂足为E.
(1)求证:△ABD≌△EDB;
(2)只需添加一个条件,即 等,可使四边形ABCD为矩形.请加以证明.
4、已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
知识点三、正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形是在平行四边形的前提下定义的,它包含两层意思:
①有一组邻边相等的平行四边形
(菱形)
②有一个角是直角的平行四边形
(矩形)
2、性质:
边:对边平行,四边相等;
角:四个角都是直角;
对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.
3、正方形的判定方法:
(1)有一个角是直角的菱形是正方形
(2)有一组邻边相等的矩形是正方形
(3)对角线相等的菱形是正方形
(4)对角线相互垂直的矩形是正方形
(5)对角线相互垂直平分且相等的四边形是正方形
【注意】:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是
45°;
正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.正方形具有矩形的性质,同时又具有菱形的性质.
正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形.
正方形是中心对称图形,对称中心是对角线的交点,
正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,有四条对称轴;
【练习】
1、正方形的一条对角线长为4,则这个正方形的面积是( )
A.8
B.4
C.8
D.16
2、下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
3、如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2
B.3
C.
D.
4、如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于 度.
5、已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD= 度.
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为 .
6、如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A.-1
B.3-
C.+1
D.-1
7、已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
8、已知:如图,四边形ABCD是正方形,分别过点A.
C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB.
DN分别交l2于Q.
P点.求证:四边形PQMN是正方形.
【课堂总结】
【课堂小测】
1.如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是2+2
C.四边形ACEF是平行四边形,它的周长是4
D.四边形ACEF是矩形,它的周长是4+4
2.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
3.若菱形的周长为20cm,则它的边长是 cm.
4.如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为 .
5.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是 .
6.如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
7.已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
求证:四边形ABCD为菱形.
8、矩形具有而菱形不具有的性质是(
)
A、四边相等
B、对角线互相垂直
C、对角线相等
D、每一条对角线平方一组对角
9、下列说法中,正确的是(
)
A、两条对角线相等的四边形是矩形
B、两条对角线互相垂直的四边形是菱形
C、两条对角线互相垂直相等的四边形是正方形
D、两条对角线互相平分的四边形是平行四边形
10、矩形的对角线长为2cm,一边长为cm,则它的面积为(
)
A、1cm?
B、2cm?
C、cm2
D、4
cm2
11、如图,正方形ABCD中,AC、BD相交于O,点E在AC上,且AE=AB,则∠OBE=(
)
A、15°
B、22.5°
C、25°
D、30°
12、如图,已知在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F
(1)求证:△BED≌△CFD
(2)若∠A=90°,求证:四边形DFAE是正方形
13、如图,在△ABC中,∠BAC
=
90°,D、E、F分别是BC、CA、AB边的中点,
求证:(1)四边形AFDE是矩形;
(2)当△ABC满足
条件时,四边形AFDE是正方形,请你说明理由。
14、如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A.
B.2
C.2
D.1
15、如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
A.∠1<∠2
B.∠1>∠2
C.∠3<∠4
D.∠3>∠4
16、附图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( )
A.2
B.3
C.12﹣4
D.6﹣6
17、如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
B.3-
C.+1
D.-1
18、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16
B.17
C.18
D.19
19、已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
20、下列判断中正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
21、如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )
A.22.5°角
B.30°角
C.45°角
D.60°角
学生姓名
性别
年级
初三
学科
数学
授课教师
上课时间
年
月
日
第(
)次课
共(
)次课
课时:3课时
教学课题
特殊的平行四边形
教学目标
1、理解菱形、矩形、正方形的定义、性质
2、能运用判定方法来证明。
3、会用菱形、矩形、正方形的性质解决简单的证明和计算问题;
教学重点与难点
重点:.矩形、正方形的性质、判定以及判定的应用
难点:相关知识的综合应用
一.
作业检查
作业完成情况:优□
良□
中□
差□
二.
内容回顾
回顾上节课内容.
知识梳理
知识点一、菱形
1.菱形的性质
(1)菱形的定义:
有一组邻边相等的平行四边形叫做菱形.(平行四边形+一组邻边相等=菱形)
(2)菱形的性质:
菱形具有平行四边形的一切性质;
A、边:对边平行且相等
B、角:菱形的对角相等,邻角互补
C、对角线:两条对角线互相平分且垂直
每一条对角线平分一组对角
D、对称性:中心对称:对角线的交点就是对称中心
轴对称:有两条对称轴。即:两条对角线所在的直线
(3)菱形的面积计算
①利用平行四边形的面积公式.
②菱形面积=1/2ab.(a、b是两条对角线的长度)
【练习】
1、边长为3cm的菱形的周长是( )
A.6cm
B.9cm
C.12cm
D.15cm
2、
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1
B.
C.2
D.2
3、
如图,四边形ABCD是菱形,对角线AC=8,DB=6,DE⊥BC于点E,则DE的长为( )
A.2.4
B.3.6
C.4.8
D.6
4、在菱形ABCD中,若对角线的长AC=8cm,BD=6cm,则边长
AB=
cm.
如图,在菱形ABCD中,AB=10,AC=12,则它的面积是 .
6、如图,菱形ABCD中,AC、BD相交于点O,若∠BCO=55°,则∠ADO= °.
7、
如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
菱形的判定
3、相关知识点
A、线段垂直平分线的性质
①垂直平分线垂直且平分其所在线段.
②垂直平分线上任意一点,到线段两端点的距离相等.
③三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.
B、直角三角形斜边上的中线
性质:在直角三角形中,斜边上的中线等于斜边的.
勾股定理(相关知识点)
【练习】
1、如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28°
B.52°
C.62°
D.72°
2、
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
3、如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于( )
A.100°
B.104°
C.105°
D.110°
如图,菱形ABCD的周长为12cm,BC的垂直平分线EF经过点A,则对角线BD的长是 cm.
5.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是 .
6.如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
7.已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
求证:四边形ABCD为菱形.
8.如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?
9、已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
10、已知:如图四边形ABCD的对角线AC的垂直平分线与边AD,
BC分别交于E,
F.求证:四边形AFCE是菱形.
11、已知如图,菱形ABCD中,E是BC上一点,AE,
BD交于M,若AB=AE,∠EAD=2∠BAE.求证:AM=BE.
12、如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.求线段BE的长.
13、如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC,交BC的延长线于F.请你猜想DE与DF的大小有什么关系?并证明你的猜想
12、如图,菱形ABCD的边长为2,BD=2,E,
F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
知识点二、矩形
1.
矩形的定义:有一个角是直角的平行四边形是矩形。
2.
矩形的性质:A、边:对边平行且相等
B、四个角都是直角
C、对角线相等且平分
3、拓展:
直角三角形性质定理:直角三角形斜边上的中线等于斜边的一半。
练习:
1、如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为( )
A.30°
B.60°
C.90°
D.120°
2、如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90°
B.AC=BD
C.OA=OB
D.OA=AD
3、
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
5、如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是 .
6、
若平行四边形的两条对角线长为6
cm和16
cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm
B.8cm
C.12cm
D.16cm
7、如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为( )
A.6cm
B.4cm
C.2cm
D.1cm
8、如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为( )
A.1
B.2
C.3
D.4
矩形的判定
角:
判定一:有三个角是直角的四边形是矩形。
判定二:有一个角是直角的平行四边形是矩形。
对角线:
判定三:对角线相等的平行四边形是矩形。
判定四:对角线相互平分且相等的四边形是矩形。
1、如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是矩形;
(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.
2、
已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论:P
A2+PC2=PB2+PD2,请你探究:当点P分别在图(2)、图(3)中的位置时,PA2、PB2、PC2和PD2又有怎样的数量关系请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论.
答:对图(2)的探究结论为 ;
对图(3)的探究结论为 ;
3、如图,AB=CD=ED,AD=EB,BE⊥DE,垂足为E.
(1)求证:△ABD≌△EDB;
(2)只需添加一个条件,即 等,可使四边形ABCD为矩形.请加以证明.
4、已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
知识点三、正方形
定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形是在平行四边形的前提下定义的,它包含两层意思:
①有一组邻边相等的平行四边形
(菱形)
②有一个角是直角的平行四边形
(矩形)
2、性质:
边:对边平行,四边相等;
角:四个角都是直角;
对角线:对角线相等,互相垂直平分,每条对角线平分一组对角.
3、正方形的判定方法:
(1)有一个角是直角的菱形是正方形
(2)有一组邻边相等的矩形是正方形
(3)对角线相等的菱形是正方形
(4)对角线相互垂直的矩形是正方形
(5)对角线相互垂直平分且相等的四边形是正方形
【注意】:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是
45°;
正方形的两条对角线把它分成四个全等的等腰直角三角形,这是正方形的特殊性质.正方形具有矩形的性质,同时又具有菱形的性质.
正方形不仅是特殊的平行四边形,并且是特殊的矩形,又是特殊的菱形.
正方形是中心对称图形,对称中心是对角线的交点,
正方形又是轴对称图形,对称轴是对边中点的连线和对角线所在直线,有四条对称轴;
【练习】
1、正方形的一条对角线长为4,则这个正方形的面积是( )
A.8
B.4
C.8
D.16
2、下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
3、如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2
B.3
C.
D.
4、如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于 度.
5、已知E是正方形ABCD的对角线AC上一点,AE=AD,过点E作AC的垂线,交边CD于点F,那么∠FAD= 度.
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为 .
6、如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
A.-1
B.3-
C.+1
D.-1
7、已知:如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.
求证:OE=OF.
8、已知:如图,四边形ABCD是正方形,分别过点A.
C两点作l1∥l2,作BM⊥l1于M,DN⊥l1于N,直线MB.
DN分别交l2于Q.
P点.求证:四边形PQMN是正方形.
【课堂总结】
【课堂小测】
1.如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是2+2
C.四边形ACEF是平行四边形,它的周长是4
D.四边形ACEF是矩形,它的周长是4+4
2.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE= .
3.若菱形的周长为20cm,则它的边长是 cm.
4.如图,菱形ABCD中,∠A=60°,BD=7,则菱形ABCD的周长为 .
5.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是 .
6.如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
7.已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.
求证:四边形ABCD为菱形.
8、矩形具有而菱形不具有的性质是(
)
A、四边相等
B、对角线互相垂直
C、对角线相等
D、每一条对角线平方一组对角
9、下列说法中,正确的是(
)
A、两条对角线相等的四边形是矩形
B、两条对角线互相垂直的四边形是菱形
C、两条对角线互相垂直相等的四边形是正方形
D、两条对角线互相平分的四边形是平行四边形
10、矩形的对角线长为2cm,一边长为cm,则它的面积为(
)
A、1cm?
B、2cm?
C、cm2
D、4
cm2
11、如图,正方形ABCD中,AC、BD相交于O,点E在AC上,且AE=AB,则∠OBE=(
)
A、15°
B、22.5°
C、25°
D、30°
12、如图,已知在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F
(1)求证:△BED≌△CFD
(2)若∠A=90°,求证:四边形DFAE是正方形
13、如图,在△ABC中,∠BAC
=
90°,D、E、F分别是BC、CA、AB边的中点,
求证:(1)四边形AFDE是矩形;
(2)当△ABC满足
条件时,四边形AFDE是正方形,请你说明理由。
14、如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A.
B.2
C.2
D.1
15、如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
A.∠1<∠2
B.∠1>∠2
C.∠3<∠4
D.∠3>∠4
16、附图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( )
A.2
B.3
C.12﹣4
D.6﹣6
17、如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
B.3-
C.+1
D.-1
18、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16
B.17
C.18
D.19
19、已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )
A.∠D=90°
B.AB=CD
C.AD=BC
D.BC=CD
20、下列判断中正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线互相垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
21、如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )
A.22.5°角
B.30°角
C.45°角
D.60°角
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
