人教版数学七年级下册 第10章课时 能力检测(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级下册 第10章课时 能力检测(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 585.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 13:31:32 | ||
图片预览



文档简介
10.1统计调查
一.选择题
1.下列调查中,适宜采用全面调查方式的是( )
A.了解一批圆珠笔的寿命
B.了解市民对“新型冠状病毒”的知晓程度
C.了解全国七年级学生身高的现状
D.检查一枚用于发射卫星的运载火箭的各零部件
2.为了解七年级4000名学生参加数学统测成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是( )
A.样本容量是200名
B.每名学生是个体
C.200名学生的数学成绩是总体的一个样本
D.4000名学生是总体
3.某区为了传承中华优秀传统文化,组织了一次全区600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析,在这个问题中,下列说法,其中正确的有( )
①这600名学生的“中华经典诵读”大赛成绩的全体是总体;
②每个学生是个体;
③50名学生是总体的一个样本.
A.0个 B.1个 C.2个 D.3个
4.今年我县有1200名考生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:①这1200名考生的数学中考成绩的全体是总体;②每个考生是个体;③200名考生是总体的一个样本;④样本的容量是200.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
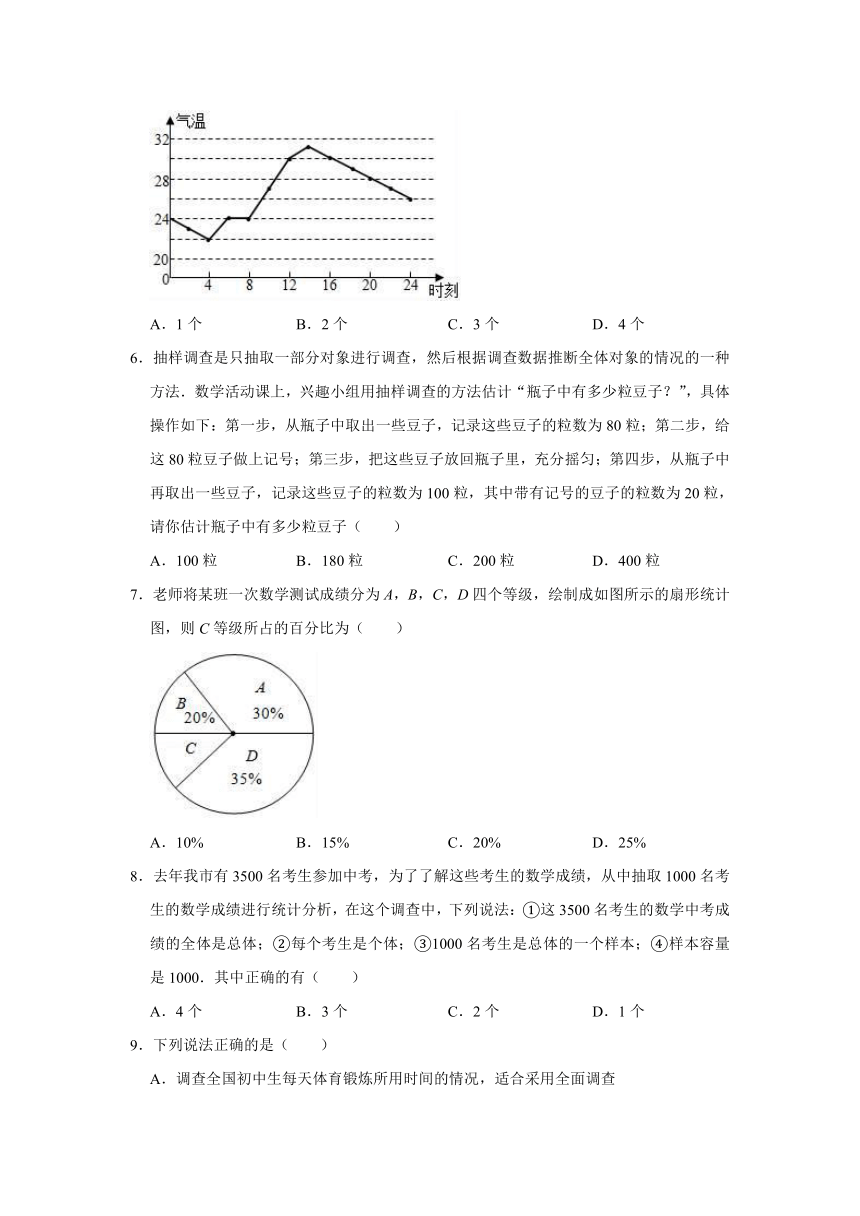
5.如图,折线图描述的是某地某日的气温变化情况,由图可知气温为24℃的整点时刻有( )
A.1个 B.2个 C.3个 D.4个
6.抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
7.老师将某班一次数学测试成绩分为A,B,C,D四个等级,绘制成如图所示的扇形统计图,则C等级所占的百分比为( )
A.10% B.15% C.20% D.25%
8.去年我市有3500名考生参加中考,为了了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这3500名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000名考生是总体的一个样本;④样本容量是1000.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.下列说法正确的是( )
A.调查全国初中生每天体育锻炼所用时间的情况,适合采用全面调查
B.调查黄河某段的水质情况,适合采用抽样调查
C.为了了解神舟飞船的设备零件的质量情况,选择抽样调查
D.为了了解一批袋装食品是否含有防腐剂,选择全面调查
10.下列调查方式,你认为最合适的是( )
A.调查市场上某种白酒的塑化剂的含量,采用全面调查方式
B.调查鞋厂生产的鞋底能承受的弯折次数,采用全面调查方式
C.调查端午节期间市场上粽子的质量,采用抽样调查方式
D.“长征﹣3B火箭”发射前,检查其各零部件的合格情况,采用抽样调查的方式
二.填空题
11.某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 .
12.质检部门从1000件电子元件中随机抽取100件进行检测,其中有2件是次品.试据此估计这批电子元件中大约有 件次品.
13.疫情期间,张老师为了了解本班学生居家学习期间每天体育锻炼的情况.张老师随机抽查了本班20名学生,统计数据如表所示:
每天锻炼时间(小时) 0.5 1 1.5 2
人数 4 5 6 5
若这20名学生每天体育锻炼时间的平均数为m小时,则m的值为 .
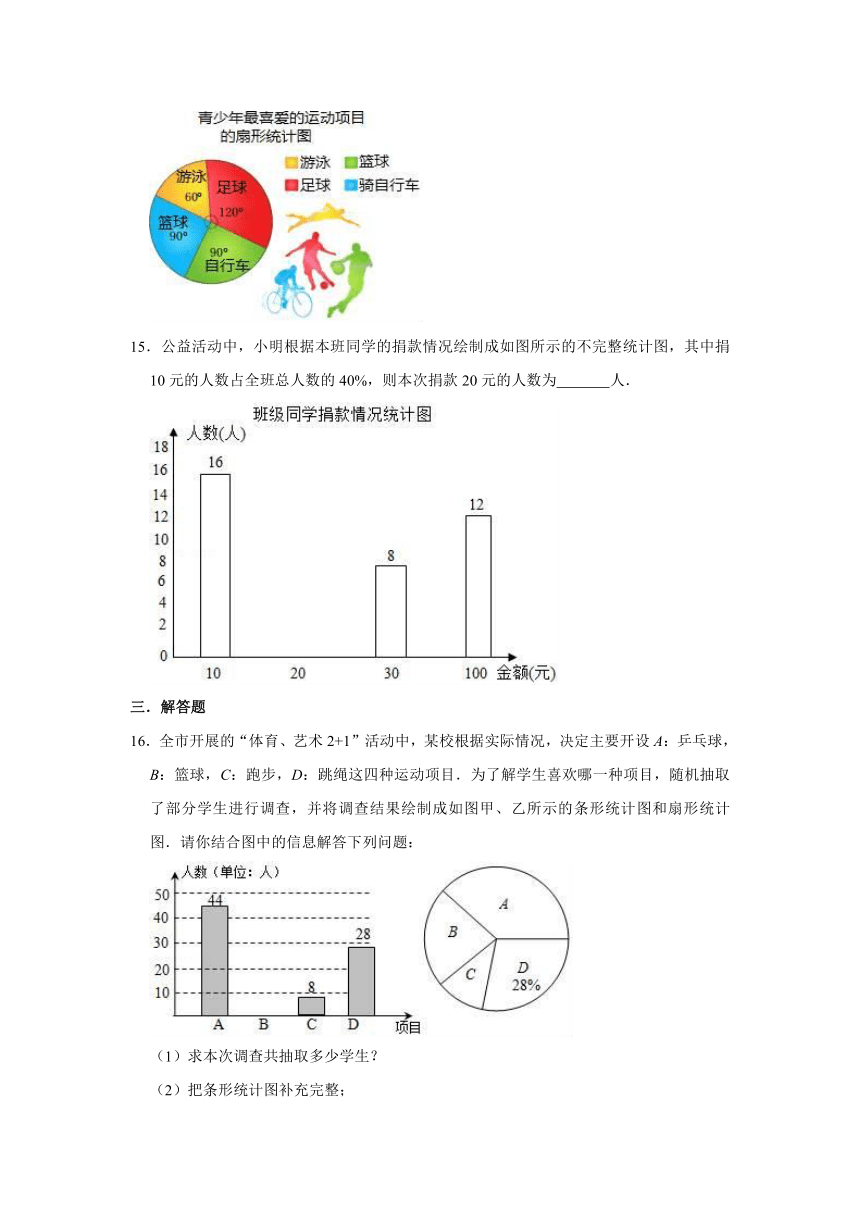
14.在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
15.公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
三.解答题
16.全市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)求本次调查共抽取多少学生?
(2)把条形统计图补充完整;
(3)求扇形统计图中B所对的圆心角的度数.
17.市消费者协会对销量较大的A,B,C三种奶粉进行了问卷调查,发放问卷540份(问卷由单选和多选题组成),对收回的476份问卷进行了整理,部分数据如下:最近一次购买各品牌奶粉用户的比例如图;用户对各品牌奶粉满意情况如下表:
内容 质量 广告 价格
品牌 A B C A B C A B C
满意的用户/人 384 242 234 326 344 214 196 192 200
根据上述信息回答下列问题:
(1)A品牌奶粉的主要竞争优势是什么?你是怎样看出来的?
(2)广告对用户选择品牌有影响吗?请简要说明理由.
(3)你对厂家有何建议?
18.学校为了解疫情期间学生自习课落实“停课不停学,学习不延期”在线学习的效果,王校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A:阅读电子读物,B:听教师录播课程,C:完成在线作业,D:线上讨论交流.并根据调查结果绘制成如图两幅不完整的统计图,根据图中信息,解答下列问题:
(1)王校长本次抽查了 名学生;
(2)将条形统计图补充完整;
(3)求扇形统计图中“C.完成在线作业”对应的圆心角的度数;
(4)该校在线学习的学生共有3200名,请估计当时全校“B.听教师录播课程”的约有多少名学生?
19.(1)2019年4月,中国新闻出版研究院发布了《第十六次全国国民阅读调查报告》.图1是小明根据该报告提供的数据制作的“2017~2018年我国未成年人图书阅读率统计图”的一部分.
报告中提到,2018年9~13周岁少年儿童图书阅读率比2017年提高了3.1个百分点,2018年我国0~17周岁未成年人图书阅读率为80.4%,比2017年下降了4.4个百分点.
根据以上信息解决下列问题:
①写出图1中a的值;
②补全图1;
(2)读书社的小明在搜集资料的过程中,发现了《人民日报》曾经介绍过多种阅读法,他在班上给同学们介绍了其中6种,并调查了全班40名同学对这6种阅读法的认可程度,制作了如图的统计表和统计图(如图2):
最愿意使用的阅读方法人数统计表
阅读方法类型 划记 人数
A.读书不二法
4
B.比较品读法 正 5
C.字斟句酌法
D.精华提炼法 正正 10
E.多维研读法
6
F.角色扮演法
7
合计 40 40
根据以上信息解决下列问题:
①补全统计表及图2;
②根据调查结果估计全年级500名同学最愿意使用“C.字斟句酌法”的人数.
参考答案与试题解析
一.选择题
1.【解答】解:A、了解一批圆珠笔的寿命,适合宜采抽样调查,故本选项不合题意;
B了解市民对“新型冠状病毒”的知晓程度,适合宜采抽样调查,故本选项不合题意;
C、了解全国七年级学生身高的现状,适合宜采抽样调查,故本选项不合题意;
D、检查一枚用于发射卫星的运载火箭的各零部件,适合采用全面调查,故本选项符合题意.
故选:D.
2.【解答】解:A.样本容量是200,故本选项不合题意;
B.每名学生的数学成绩是个体,故本选项不合题意;
C.200名学生的数学成绩是总体的一个样本,故本选项符合题意;
D.4000名学生的数学成绩是总体,故本选项不合题意.
故选:C.
3.【解答】解:①这600名学生的“中华经典诵读”大赛成绩的全体是总体,说法正确;
②每个学生的“中华经典诵读”大赛成绩是个体,故原说法错误;
③50名学生的“中华经典诵读”大赛成绩是总体的一个样本,故原说法错误.
所以正确的有1个.
故选:B.
4.【解答】解:①这1200名考生的数学中考成绩的全体是总体,说法正确;
②每个考生的数学成绩是个体,故命题错误;
③200名考生的数学成绩是总体的一个样本,故命题错误;
④样本容量是200,说法正确.
所以说法正确的有2个.
故选:B.
5.【解答】解:由折线图可得:气温为24℃的整点时刻为0点,6点,7点,8点共有4个,
故选:D.
6.【解答】解:设瓶子中有x粒豆子,根据题意得:
=,
解得:x=400,
经检验x=400是原方程的解,
答:估计瓶子中豆子的数量约为400粒.
故选:D.
7.【解答】解:C等级所占的百分比为:1﹣20%﹣35%﹣30%=15%.
故选:B.
8.【解答】解:①这3500名考生的数学中考成绩的全体是总体,此结论正确;
②每个考生的数学成绩是个体,此结论错误;
③1000名考生的数学成绩是总体的一个样本,此结论错误;
④样本容量是1000,此结论正确.
故选:C.
9.【解答】解:A.调查全国初中生每天体育锻炼所用时间的情况,适合采用抽样调查的方式,故本选项不合题意;
B.调查黄河某段的水质情况,适合采用抽样调查的方式,故本选项符合题意;
C.为了了解神舟飞船的设备零件的质量情况,适合采用普查的方式,故本选项不合题意;
D.为了了解一批袋装食品是否含有防腐剂,适合采用抽样调查的方式,故本选项不合题意.
故选:B.
10.【解答】解:A、调查市场上某种白酒的塑化剂的含量,采用全面调查方式,适合抽样调查;
B、了调查鞋厂生产的鞋底能承受的弯折次数,适合抽样调查;
C、调查端午节期间市场上粽子的质量,适合采用抽样调查方式;
D、“长征﹣3B火箭”发射前,检查其各零部件的合格情况,适合采用全面调查方式;
故选:C.
二.填空题(共5小题)
11.【解答】解:“来自甲地区的学生”对应扇形的圆心角的度数为360°×=150°,
故答案为:150°.
12.【解答】解:1000×=20(件),
即这批电子元件中大约有20件次品,
故答案为:20.
13.【解答】解:m=
=
=1.3.
故答案为:1.3.
14.【解答】解:根据题意,可得30÷(﹣)=360(人),
即参加这次调查的总人数是360人.
故答案为:360.
15.【解答】解:∵捐10元的有16人,占全班总人数的40%,
∴全班的总人数为16÷40%=40(人),
则捐款20元的人数为40﹣(16+8+12)=4(人),
故答案为:4.
三.解答题(共4小题)
16.【解答】解:(1)调查的人数是:28÷28%=100(人);
(2)喜欢B的人数是:100﹣44﹣8﹣28=20(人);
补全条形统计图为:
(3)B占调查学生的百分比为:=20%.
所以B所对的圆心角为:360°×20%=72°.
答:扇形统计图中B所对的圆心角的度数为72°.
17.【解答】解:(1)A品牌奶粉主要竞争优势是质量,可以从以下看出:
①对A品牌的质量满意的用户最多;
②对A品牌的广告、价格满意的用户不是最多.
(2)广告对用户选择品牌有影响,可以从以下看出:
①对B、C品牌质量、价格满意的用户相差不大;
②对B品牌的广告满意的用户多于C品牌,且相差较大;
③购买B品牌的用户比例高于C品牌.
(3)建议:①重视质量,
②在保证质量的前提下,要关注广告和价格.
18.【解答】解:(1)王校长本次抽查的学生有:18÷20%=90(名);
故答案为:90;
(2)线上讨论交流的人数有90﹣18﹣36﹣24=12(人),补全统计图如下:
(3)扇形统计图中“完成在线作业”对应的圆心角的度数为360°×=96°;
(4)根据题意得:
3200×=1280(名),
答:当时全校“B.听教师录播课程”的约有1280名学生.
19.【解答】解:(1)①∵2018年9~13周岁少年儿童图书阅读率比2017年提高了3.1个百分点,
∴a=96.3%﹣3.1%=93.2%,
即a的值是93.2%;
②∵2018年我国0~17周岁未成年人图书阅读率为80.4%,比2017年下降了4.4个百分点,
∴2017年我国0~17周岁未成年人图书阅读率为80.4+4.4%=84.8%,
补全的图1如右图所示;
(2)①选择C的有:40﹣4﹣5﹣10﹣6﹣7=8(人),
C所占的百分比为:8÷40×100%=20%,
D所占的百分比为:10÷40×100%=25%,
补全的统计表及图2如下图所示;
阅读方法类型 划记 人数
A.读书不二法
4
B.比较品读法 正 5
C.字斟句酌法
8
D.精华提炼法 正正 10
E.多维研读法
6
F.角色扮演法
7
合计 40 40
故答案为:,8;
②500×20%=100(人),
即全年级500名同学最愿意使用“C.字斟句酌法”的有100人.
10.2直方图
一.选择题
1.2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重,并绘制成了频数分布直方图,从左往右数每个小长方形的长度之比为2:3:4:1,其中第三组的频数为( )
A.80人 B.60人 C.20人 D.10人
2.小明在做“抛一枚正六面体骰子”的实验时,他连续抛了10次,共抛出了3次“6”向上,则出现“6”向上的频率是( )
A. B. C. D.
3.一个班有40名学生,在期末体育考核中,达到优秀的有18人,合格(但没达到优秀)的有17人,则这次体育考核中,不合格人数的频率是( )
A.0.125 B.0.45 C.0.425 D.1.25
4.如图是某班一次数学测试成绩的频数直方图,则成绩在69.5~89.5分范围内的学生共有( )
A.24人 B.10人 C.14人 D.29人
5.数学老师将数学期末模拟考试的成绩整理后,绘制成如图所示的频数分布直方图,下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的分数段的频数为2
D.得分及格(≥60分)约有12人
6.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
7.某校随机抽查若干名学生,测试了1分钟仰卧起坐的次数,把所得数据绘制成频数分布直方图(如图),则仰卧起坐次数不小于15次且小于20次的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
8.合肥市教育教学研究室为了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:A等,130~150分;B等,110分~129分;C等,90分~109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 频数 频率
A
0.2
B
C 6
D 2 0.1
合计
1
根据图表中的信息,下列说法中不正确的是( )
A.这次抽查了20名学生参加一模考试的数学成绩
B.这次一模考试中,考生数学成绩为B等次的频率为0.4
C.根据频数分布直方图制作的扇形统计图中等次C所占的圆心角为105°
D.若全市有20000名学生参加中考一模考试,则估计数学成绩达到B等次及以上的人数有12000人
9.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
10.体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
二.填空题
11.一个样本容量为50的样本最大值为127,最小值为60,组距为10,则可分成 组.
12.在某个频数分布直方图中,共有11个小长方形,若中间一个长方形的高等于其它10个小长方形高之和的,且样本容量是60,则中间一组的频数是 .
13.对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
14.某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
15.小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
三.解答题
16.受新冠病毒影响,2020年春浙江省中小学延期开学,复学后,某校为了解学生对防疫知识的掌握情况,学校组织全体学生进行防疫知识竞赛.从中抽取了8%的学生的竞赛成绩(满分100,成绩为整数)作为样本,整理后绘制成如图所示的频数直方图.请结合直方图解答下列问题:
(1)求此次抽取的样本容量及全校学生人数.
(2)求竞赛成绩在84.5~89.5这一组的频率.
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计全校学生中约有多少人获得奖励.
17.在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:
A.从某所普通中学校随机选取200名学生作为调查对象进行调查;
B.从市内某区的不同学校中随机选取200名学生作为调查对象进行调查;
C.从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查.
(1)在上述调查方式中,你认为比较合理的一个是 (填番号).
(2)如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m= .
(3)已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
18.某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
19.2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
参考答案与试题解析
一.选择题
1.【解答】解:根据题意知,第三组的频数为200×=80(人),
故选:A.
2.【解答】解:由题意得,出现“6”向上的频率是,
故选:A.
3.【解答】解:不合格人数为40﹣18﹣17=5,
∴不合格人数的频率是=0.125,
故选:A.
4.【解答】解:成绩在69.5~89.5分范围内的学生共有:10+14=24(人),
故选:A.
5.【解答】解:A、得分在70~80分的人数最多,正确,本选项不符合题意.
B、该班的总人数为40,正确,本选项不符合题意.
C、人数最少的分数段的频数为2,正确,本选项不符合题意.
D、得分及格(≥60分)约有12人,错误,应该有36人,本选项符合题意.
故选:D.
6.【解答】解:由图知,学生仰卧起坐次数不少于20的人数为10+12+5=27(人),
所以学生仰卧起坐次数不少于20的频率为27÷30=0.9,
故选:D.
7.【解答】解:仰卧起坐次数不小于15次且小于20次的频率是:=0.1;
故选:A.
8.【解答】解:A.本次抽查的学生数学成绩数量为2÷0.1=20,此选项正确;
B.A等次的数量为20×0.2=4,则B等次的数量为20﹣(4+6+2)=8,所以考生数学成绩为B等次的频率为8÷20=0.4,此选项正确;
C.根据频数分布直方图制作的扇形统计图中等次C所占的圆心角为360°×=108°,此选项错误;
D.估计数学成绩达到B等次及以上的人数有20000×(0.2+0.4)=12000人,此选项正确;
故选:C.
9.【解答】解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
10.【解答】解:读图可知:
共有(4+12+6+20+8)=50人,
其中最喜欢篮球的有20人,
故频率最喜欢篮球的频率=20÷50=0.4.
故选:D.
二.填空题(共5小题)
11.【解答】解:∵样本最大值为127,最小值为60,
∴极差为127﹣60=67,
∵组距为10,
∴67÷10=6.7,
∴此样本可分成7组,
故答案为:7.
12.【解答】解:设中间一组的频率是x,那么其它各组频率的和是1,根据题意得
x+4x=1,
解得x=0.2,
60×0.2=12.
故中间一组的频数是12.
故答案为:12.
13.【解答】解:∵第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,且最后一组的频数为12,
∴第三组的频数为24,
则这次调查抽取的样本容量是9+15+24+16+12=76,
故答案为:76.
14.【解答】解:3000×[10(0.002+0.006+0.012)]=600,
答:这3000名学生在该次数学考试中成绩小于60分的学生数是600人.
故答案为:600人.
15.【解答】解:身高在160cm和170cm之间同学人数:一班26人,二班13人,三班18人,
因此可挑选空间最大的是一班,
故答案为:1班.
三.解答题(共4小题)
16.【解答】解:(1)样本容量:4+10+16+13+7=50,
全校学生数:50÷8%=625(人),
答:此次抽取的样本容量是50,全校学生人数为625人;
(2)16÷50=0.32,
答:竞赛成绩在84.5~89.5这一组的频率是0.32;
(3)625×=250(人),
答:全校学生中约有250人获得奖励.
17.【解答】解:(1)由题意可得,
从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查比较合理,
故选:C;
(2)m=200﹣92﹣36﹣18=54,
故答案为:54;
(3)100×=54(万),
答:全市每天“停课不停学”的学习时间在1~2小时及以上的人数有54万人;
(4)这个调查设计有不合理的地方,如在100万人的总体中,随机抽取的200人作为样本,样本容量偏小,会导致调查的结果不够准确,建议增大样本容量.
18.【解答】解:(1)140÷0.7=200(人)
答:参加本次测试的学生数为200人,
200﹣140﹣36﹣6=18(人),
故答案为:18;
(2)6÷200=0.03,
答:体质健康成绩属于“不及格”等级的频率为0.03;
(3)1800×=1584(人),
答:达到“良好”及以上等级的学生数为1584人.
19.【解答】解:(1)16÷0.08=200,
m=200×0.35=70,n=24÷200=0.12;
故答案为200,70;0.12;
(2)如图,
(3)8000×(0.08+0.2)=2240,
所以该校安全意识不强的学生约有2240人.
10.3《课题学习》
一、选择题
1.想表示某一城市一天中气温变化的情况,一般选用( )
A.条形图 B.扇形图 C.折线图 D.直方图
2.青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?( )
A.100只 B.150只 C.180只 D.200只
3.为鼓励市民珍惜每一滴水,某居委会表扬了100个节约用水模范户,5月份这100户节约用水的情况如下表:
则5月份这100户平均节水的吨数为(精确到0.01吨)( )
A.1.00吨 B.1.15吨 C.1.23吨 D.无法确定
4.某校为了了解九年级学生的体能情况,随机抽查了其中30名学生,测试了他们做1min仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示计算仰卧起坐次数在25~30次的频率是( ).
A.0.1 B.0.2 C.0.3 D.0.4
5.小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
A.各项消费金额占消费总金额的百分比
B.各项消费的金额
C.消费的总金额
D.各项消费金额的增减变化情况
6.为了支援地震灾区同学,某校开展捐书活动,九(1)班40名同学积极参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
二、填空题
7.如图是某校七年一班全班同学1min心跳次数频数直方图,那么,心跳次数在_______之间的学生最多,占统计人数的_____%.(精确到1%)
8.为响应“红歌唱响中国”活动,某乡镇举行了一场“红歌”歌咏比赛,组委会规定:任何一名参赛选手的成绩x满足:60≤x<100,赛后整理所有参赛选手的成绩如下表:
根据表中提供的信息得到n=__________.
9.某中学七年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息可知a的值为__________.
10.七年二班50名同学的一次考试成绩频数分布直方图如图所示,则71~90分之间有____人.
三、解答题
11.已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
12.为了了解学校开展“孝敬父母,从家务事做起”活动的实施情况,该校抽取八年级50名学生调查他们一周(按7天计算)做家务所用时间(单位:小时,调查结果保留一位小数),得到一组数据,并绘制成统计表,请根据表完成下列各_é??_:
(1)填写频率分布表中末完成的部分.
(2)由以上信息判断,每周做家务的时间不超过1.5h的学生所占的百分比是________.
(3)针对以上情况,写一个20字以内倡导“孝敬父母,热爱劳动”的句子.
13.为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50名学生进行1min跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下图所示.
请结合图表完成下列问_é??_.
(1)表中的a=______.
(2)请把频数直方图补充完整.
(3)若八年级学生1min跳绳次数(x)达标要求是:x<120为不合格,120≤x<140为合格,140≤x<160为良,x≥160为优,根据以上信息,请你给学校或八年级同学提一条合理化建议.
14.在某市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
(1)样本中喜欢B项目的人数百分比是________;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
15.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
(1)填空:a=______,b=________;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165 cm的学生大约有多少人?
参考答案
答案为:C
答案为:D
答案为:B
答案为:D
答案为:A
答案为:B
答案为:59.5~69.5,48;
答案为:0.3
答案为:14
答案为:27
解:(1)计算最大值与最小值的差:32-23=9.
(2)确定组数与组距:已知组距为2,则4.5,因此定为5组.
(3)决定分点,所分的五个小组是:
22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5,30.5~32.5.
(4)列频数分布表:
(5)画频数分布直方图:
解:(1)表格中空缺部分自上而上依次为:0.14,0.06,2.
(2)58%
(3)如:“体验生活,锻炼自我,珍惜母爱,勤奋好学”等.
解:(1)a=12 (2)图略 (3)只要合理即可.
解:(1) 20%
(2) 总人数是44÷44%=100(人),
∴B项目的人数是100×20%=20(人),补图略
(3)1000×44%=440(人),则全校喜欢乒乓球的人数是440人
解:(1) 10 28%
(2)补图略
(3)600×(28%+12%)=240(人),估计身高不低于165 cm的学生大约有240人
一.选择题
1.下列调查中,适宜采用全面调查方式的是( )
A.了解一批圆珠笔的寿命
B.了解市民对“新型冠状病毒”的知晓程度
C.了解全国七年级学生身高的现状
D.检查一枚用于发射卫星的运载火箭的各零部件
2.为了解七年级4000名学生参加数学统测成绩的情况,从中随机抽取200名学生的数学成绩进行分析.下列说法正确的是( )
A.样本容量是200名
B.每名学生是个体
C.200名学生的数学成绩是总体的一个样本
D.4000名学生是总体
3.某区为了传承中华优秀传统文化,组织了一次全区600名学生参加的“中华经典诵读”大赛.为了解本次大赛的选手成绩,随机抽取了其中50名选手的成绩进行统计分析,在这个问题中,下列说法,其中正确的有( )
①这600名学生的“中华经典诵读”大赛成绩的全体是总体;
②每个学生是个体;
③50名学生是总体的一个样本.
A.0个 B.1个 C.2个 D.3个
4.今年我县有1200名考生参加中考,为了了解这些考生的数学成绩,从中抽取200名考生的数学成绩进行统计分析,在这个问题中,下列说法:①这1200名考生的数学中考成绩的全体是总体;②每个考生是个体;③200名考生是总体的一个样本;④样本的容量是200.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,折线图描述的是某地某日的气温变化情况,由图可知气温为24℃的整点时刻有( )
A.1个 B.2个 C.3个 D.4个
6.抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
7.老师将某班一次数学测试成绩分为A,B,C,D四个等级,绘制成如图所示的扇形统计图,则C等级所占的百分比为( )
A.10% B.15% C.20% D.25%
8.去年我市有3500名考生参加中考,为了了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,在这个调查中,下列说法:①这3500名考生的数学中考成绩的全体是总体;②每个考生是个体;③1000名考生是总体的一个样本;④样本容量是1000.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
9.下列说法正确的是( )
A.调查全国初中生每天体育锻炼所用时间的情况,适合采用全面调查
B.调查黄河某段的水质情况,适合采用抽样调查
C.为了了解神舟飞船的设备零件的质量情况,选择抽样调查
D.为了了解一批袋装食品是否含有防腐剂,选择全面调查
10.下列调查方式,你认为最合适的是( )
A.调查市场上某种白酒的塑化剂的含量,采用全面调查方式
B.调查鞋厂生产的鞋底能承受的弯折次数,采用全面调查方式
C.调查端午节期间市场上粽子的质量,采用抽样调查方式
D.“长征﹣3B火箭”发射前,检查其各零部件的合格情况,采用抽样调查的方式
二.填空题
11.某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 .
12.质检部门从1000件电子元件中随机抽取100件进行检测,其中有2件是次品.试据此估计这批电子元件中大约有 件次品.
13.疫情期间,张老师为了了解本班学生居家学习期间每天体育锻炼的情况.张老师随机抽查了本班20名学生,统计数据如表所示:
每天锻炼时间(小时) 0.5 1 1.5 2
人数 4 5 6 5
若这20名学生每天体育锻炼时间的平均数为m小时,则m的值为 .
14.在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
15.公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
三.解答题
16.全市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
(1)求本次调查共抽取多少学生?
(2)把条形统计图补充完整;
(3)求扇形统计图中B所对的圆心角的度数.
17.市消费者协会对销量较大的A,B,C三种奶粉进行了问卷调查,发放问卷540份(问卷由单选和多选题组成),对收回的476份问卷进行了整理,部分数据如下:最近一次购买各品牌奶粉用户的比例如图;用户对各品牌奶粉满意情况如下表:
内容 质量 广告 价格
品牌 A B C A B C A B C
满意的用户/人 384 242 234 326 344 214 196 192 200
根据上述信息回答下列问题:
(1)A品牌奶粉的主要竞争优势是什么?你是怎样看出来的?
(2)广告对用户选择品牌有影响吗?请简要说明理由.
(3)你对厂家有何建议?
18.学校为了解疫情期间学生自习课落实“停课不停学,学习不延期”在线学习的效果,王校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种):A:阅读电子读物,B:听教师录播课程,C:完成在线作业,D:线上讨论交流.并根据调查结果绘制成如图两幅不完整的统计图,根据图中信息,解答下列问题:
(1)王校长本次抽查了 名学生;
(2)将条形统计图补充完整;
(3)求扇形统计图中“C.完成在线作业”对应的圆心角的度数;
(4)该校在线学习的学生共有3200名,请估计当时全校“B.听教师录播课程”的约有多少名学生?
19.(1)2019年4月,中国新闻出版研究院发布了《第十六次全国国民阅读调查报告》.图1是小明根据该报告提供的数据制作的“2017~2018年我国未成年人图书阅读率统计图”的一部分.
报告中提到,2018年9~13周岁少年儿童图书阅读率比2017年提高了3.1个百分点,2018年我国0~17周岁未成年人图书阅读率为80.4%,比2017年下降了4.4个百分点.
根据以上信息解决下列问题:
①写出图1中a的值;
②补全图1;
(2)读书社的小明在搜集资料的过程中,发现了《人民日报》曾经介绍过多种阅读法,他在班上给同学们介绍了其中6种,并调查了全班40名同学对这6种阅读法的认可程度,制作了如图的统计表和统计图(如图2):
最愿意使用的阅读方法人数统计表
阅读方法类型 划记 人数
A.读书不二法
4
B.比较品读法 正 5
C.字斟句酌法
D.精华提炼法 正正 10
E.多维研读法
6
F.角色扮演法
7
合计 40 40
根据以上信息解决下列问题:
①补全统计表及图2;
②根据调查结果估计全年级500名同学最愿意使用“C.字斟句酌法”的人数.
参考答案与试题解析
一.选择题
1.【解答】解:A、了解一批圆珠笔的寿命,适合宜采抽样调查,故本选项不合题意;
B了解市民对“新型冠状病毒”的知晓程度,适合宜采抽样调查,故本选项不合题意;
C、了解全国七年级学生身高的现状,适合宜采抽样调查,故本选项不合题意;
D、检查一枚用于发射卫星的运载火箭的各零部件,适合采用全面调查,故本选项符合题意.
故选:D.
2.【解答】解:A.样本容量是200,故本选项不合题意;
B.每名学生的数学成绩是个体,故本选项不合题意;
C.200名学生的数学成绩是总体的一个样本,故本选项符合题意;
D.4000名学生的数学成绩是总体,故本选项不合题意.
故选:C.
3.【解答】解:①这600名学生的“中华经典诵读”大赛成绩的全体是总体,说法正确;
②每个学生的“中华经典诵读”大赛成绩是个体,故原说法错误;
③50名学生的“中华经典诵读”大赛成绩是总体的一个样本,故原说法错误.
所以正确的有1个.
故选:B.
4.【解答】解:①这1200名考生的数学中考成绩的全体是总体,说法正确;
②每个考生的数学成绩是个体,故命题错误;
③200名考生的数学成绩是总体的一个样本,故命题错误;
④样本容量是200,说法正确.
所以说法正确的有2个.
故选:B.
5.【解答】解:由折线图可得:气温为24℃的整点时刻为0点,6点,7点,8点共有4个,
故选:D.
6.【解答】解:设瓶子中有x粒豆子,根据题意得:
=,
解得:x=400,
经检验x=400是原方程的解,
答:估计瓶子中豆子的数量约为400粒.
故选:D.
7.【解答】解:C等级所占的百分比为:1﹣20%﹣35%﹣30%=15%.
故选:B.
8.【解答】解:①这3500名考生的数学中考成绩的全体是总体,此结论正确;
②每个考生的数学成绩是个体,此结论错误;
③1000名考生的数学成绩是总体的一个样本,此结论错误;
④样本容量是1000,此结论正确.
故选:C.
9.【解答】解:A.调查全国初中生每天体育锻炼所用时间的情况,适合采用抽样调查的方式,故本选项不合题意;
B.调查黄河某段的水质情况,适合采用抽样调查的方式,故本选项符合题意;
C.为了了解神舟飞船的设备零件的质量情况,适合采用普查的方式,故本选项不合题意;
D.为了了解一批袋装食品是否含有防腐剂,适合采用抽样调查的方式,故本选项不合题意.
故选:B.
10.【解答】解:A、调查市场上某种白酒的塑化剂的含量,采用全面调查方式,适合抽样调查;
B、了调查鞋厂生产的鞋底能承受的弯折次数,适合抽样调查;
C、调查端午节期间市场上粽子的质量,适合采用抽样调查方式;
D、“长征﹣3B火箭”发射前,检查其各零部件的合格情况,适合采用全面调查方式;
故选:C.
二.填空题(共5小题)
11.【解答】解:“来自甲地区的学生”对应扇形的圆心角的度数为360°×=150°,
故答案为:150°.
12.【解答】解:1000×=20(件),
即这批电子元件中大约有20件次品,
故答案为:20.
13.【解答】解:m=
=
=1.3.
故答案为:1.3.
14.【解答】解:根据题意,可得30÷(﹣)=360(人),
即参加这次调查的总人数是360人.
故答案为:360.
15.【解答】解:∵捐10元的有16人,占全班总人数的40%,
∴全班的总人数为16÷40%=40(人),
则捐款20元的人数为40﹣(16+8+12)=4(人),
故答案为:4.
三.解答题(共4小题)
16.【解答】解:(1)调查的人数是:28÷28%=100(人);
(2)喜欢B的人数是:100﹣44﹣8﹣28=20(人);
补全条形统计图为:
(3)B占调查学生的百分比为:=20%.
所以B所对的圆心角为:360°×20%=72°.
答:扇形统计图中B所对的圆心角的度数为72°.
17.【解答】解:(1)A品牌奶粉主要竞争优势是质量,可以从以下看出:
①对A品牌的质量满意的用户最多;
②对A品牌的广告、价格满意的用户不是最多.
(2)广告对用户选择品牌有影响,可以从以下看出:
①对B、C品牌质量、价格满意的用户相差不大;
②对B品牌的广告满意的用户多于C品牌,且相差较大;
③购买B品牌的用户比例高于C品牌.
(3)建议:①重视质量,
②在保证质量的前提下,要关注广告和价格.
18.【解答】解:(1)王校长本次抽查的学生有:18÷20%=90(名);
故答案为:90;
(2)线上讨论交流的人数有90﹣18﹣36﹣24=12(人),补全统计图如下:
(3)扇形统计图中“完成在线作业”对应的圆心角的度数为360°×=96°;
(4)根据题意得:
3200×=1280(名),
答:当时全校“B.听教师录播课程”的约有1280名学生.
19.【解答】解:(1)①∵2018年9~13周岁少年儿童图书阅读率比2017年提高了3.1个百分点,
∴a=96.3%﹣3.1%=93.2%,
即a的值是93.2%;
②∵2018年我国0~17周岁未成年人图书阅读率为80.4%,比2017年下降了4.4个百分点,
∴2017年我国0~17周岁未成年人图书阅读率为80.4+4.4%=84.8%,
补全的图1如右图所示;
(2)①选择C的有:40﹣4﹣5﹣10﹣6﹣7=8(人),
C所占的百分比为:8÷40×100%=20%,
D所占的百分比为:10÷40×100%=25%,
补全的统计表及图2如下图所示;
阅读方法类型 划记 人数
A.读书不二法
4
B.比较品读法 正 5
C.字斟句酌法
8
D.精华提炼法 正正 10
E.多维研读法
6
F.角色扮演法
7
合计 40 40
故答案为:,8;
②500×20%=100(人),
即全年级500名同学最愿意使用“C.字斟句酌法”的有100人.
10.2直方图
一.选择题
1.2018年11月贵阳市教育局对某校七年级学生进行体质监测共收集了200名学生的体重,并绘制成了频数分布直方图,从左往右数每个小长方形的长度之比为2:3:4:1,其中第三组的频数为( )
A.80人 B.60人 C.20人 D.10人
2.小明在做“抛一枚正六面体骰子”的实验时,他连续抛了10次,共抛出了3次“6”向上,则出现“6”向上的频率是( )
A. B. C. D.
3.一个班有40名学生,在期末体育考核中,达到优秀的有18人,合格(但没达到优秀)的有17人,则这次体育考核中,不合格人数的频率是( )
A.0.125 B.0.45 C.0.425 D.1.25
4.如图是某班一次数学测试成绩的频数直方图,则成绩在69.5~89.5分范围内的学生共有( )
A.24人 B.10人 C.14人 D.29人
5.数学老师将数学期末模拟考试的成绩整理后,绘制成如图所示的频数分布直方图,下列说法错误的是( )
A.得分在70~80分的人数最多
B.该班的总人数为40
C.人数最少的分数段的频数为2
D.得分及格(≥60分)约有12人
6.某学校为了了解九年级体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数不少于20的频率为( )
A.0.1 B.0.17 C.0.33 D.0.9
7.某校随机抽查若干名学生,测试了1分钟仰卧起坐的次数,把所得数据绘制成频数分布直方图(如图),则仰卧起坐次数不小于15次且小于20次的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
8.合肥市教育教学研究室为了解该市所有毕业班学生参加2019年安徽省中考一模考试的数学成绩情况(满分:150分,等次:A等,130~150分;B等,110分~129分;C等,90分~109分;D等,89分及以下),从该市所有参考学生中随机抽取部分学生进行调查,并根据调查结果制作了如下的统计图表(部分信息未给出):
2019年合肥市一模数学成绩频数分布表
等次 频数 频率
A
0.2
B
C 6
D 2 0.1
合计
1
根据图表中的信息,下列说法中不正确的是( )
A.这次抽查了20名学生参加一模考试的数学成绩
B.这次一模考试中,考生数学成绩为B等次的频率为0.4
C.根据频数分布直方图制作的扇形统计图中等次C所占的圆心角为105°
D.若全市有20000名学生参加中考一模考试,则估计数学成绩达到B等次及以上的人数有12000人
9.社会主义核心价值观知识竞赛成绩结果统计如下表:成绩在91~100分的为优胜者,则优胜者的频率是( )
分段数(分) 61~70 71~80 81~90 91~100
人数(人) 1 19 22 18
A.35% B.30% C.20% D.10%
10.体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
二.填空题
11.一个样本容量为50的样本最大值为127,最小值为60,组距为10,则可分成 组.
12.在某个频数分布直方图中,共有11个小长方形,若中间一个长方形的高等于其它10个小长方形高之和的,且样本容量是60,则中间一组的频数是 .
13.对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
14.某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
15.小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
三.解答题
16.受新冠病毒影响,2020年春浙江省中小学延期开学,复学后,某校为了解学生对防疫知识的掌握情况,学校组织全体学生进行防疫知识竞赛.从中抽取了8%的学生的竞赛成绩(满分100,成绩为整数)作为样本,整理后绘制成如图所示的频数直方图.请结合直方图解答下列问题:
(1)求此次抽取的样本容量及全校学生人数.
(2)求竞赛成绩在84.5~89.5这一组的频率.
(3)如果竞赛成绩在90分以上(含90分)的同学可以获得奖励,请估计全校学生中约有多少人获得奖励.
17.在抗击新冠疫情期间,市教委组织开展了“停课不停学”的活动.为了解此项活动的开展情况,市教委督导部门准备采用以下调查方式中的一种进行调查:
A.从某所普通中学校随机选取200名学生作为调查对象进行调查;
B.从市内某区的不同学校中随机选取200名学生作为调查对象进行调查;
C.从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查.
(1)在上述调查方式中,你认为比较合理的一个是 (填番号).
(2)如图,是按照一种比较合理的调查方式所得到的数据制成的频数分布直方图,在这个调查中,所抽取200名学生每天“停课不停学”的学习时间在1~2小时之间的人数m= .
(3)已知全市共有100万学生,请你利用(2)问中的调查结果,估计全市每天“停课不停学”的学习时间在1~2小时及以上的人数有多少?
(4)你认为这个调查活动的设计有没有不合理的地方?谈谈你的理由.
18.某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
19.2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
参考答案与试题解析
一.选择题
1.【解答】解:根据题意知,第三组的频数为200×=80(人),
故选:A.
2.【解答】解:由题意得,出现“6”向上的频率是,
故选:A.
3.【解答】解:不合格人数为40﹣18﹣17=5,
∴不合格人数的频率是=0.125,
故选:A.
4.【解答】解:成绩在69.5~89.5分范围内的学生共有:10+14=24(人),
故选:A.
5.【解答】解:A、得分在70~80分的人数最多,正确,本选项不符合题意.
B、该班的总人数为40,正确,本选项不符合题意.
C、人数最少的分数段的频数为2,正确,本选项不符合题意.
D、得分及格(≥60分)约有12人,错误,应该有36人,本选项符合题意.
故选:D.
6.【解答】解:由图知,学生仰卧起坐次数不少于20的人数为10+12+5=27(人),
所以学生仰卧起坐次数不少于20的频率为27÷30=0.9,
故选:D.
7.【解答】解:仰卧起坐次数不小于15次且小于20次的频率是:=0.1;
故选:A.
8.【解答】解:A.本次抽查的学生数学成绩数量为2÷0.1=20,此选项正确;
B.A等次的数量为20×0.2=4,则B等次的数量为20﹣(4+6+2)=8,所以考生数学成绩为B等次的频率为8÷20=0.4,此选项正确;
C.根据频数分布直方图制作的扇形统计图中等次C所占的圆心角为360°×=108°,此选项错误;
D.估计数学成绩达到B等次及以上的人数有20000×(0.2+0.4)=12000人,此选项正确;
故选:C.
9.【解答】解:优胜者的频率是18÷(1+19+22+18)=0.3=30%,
故选:B.
10.【解答】解:读图可知:
共有(4+12+6+20+8)=50人,
其中最喜欢篮球的有20人,
故频率最喜欢篮球的频率=20÷50=0.4.
故选:D.
二.填空题(共5小题)
11.【解答】解:∵样本最大值为127,最小值为60,
∴极差为127﹣60=67,
∵组距为10,
∴67÷10=6.7,
∴此样本可分成7组,
故答案为:7.
12.【解答】解:设中间一组的频率是x,那么其它各组频率的和是1,根据题意得
x+4x=1,
解得x=0.2,
60×0.2=12.
故中间一组的频数是12.
故答案为:12.
13.【解答】解:∵第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,且最后一组的频数为12,
∴第三组的频数为24,
则这次调查抽取的样本容量是9+15+24+16+12=76,
故答案为:76.
14.【解答】解:3000×[10(0.002+0.006+0.012)]=600,
答:这3000名学生在该次数学考试中成绩小于60分的学生数是600人.
故答案为:600人.
15.【解答】解:身高在160cm和170cm之间同学人数:一班26人,二班13人,三班18人,
因此可挑选空间最大的是一班,
故答案为:1班.
三.解答题(共4小题)
16.【解答】解:(1)样本容量:4+10+16+13+7=50,
全校学生数:50÷8%=625(人),
答:此次抽取的样本容量是50,全校学生人数为625人;
(2)16÷50=0.32,
答:竞赛成绩在84.5~89.5这一组的频率是0.32;
(3)625×=250(人),
答:全校学生中约有250人获得奖励.
17.【解答】解:(1)由题意可得,
从市教育部门学生学籍档案中随机抽取200名学生作为调查对象进行调查比较合理,
故选:C;
(2)m=200﹣92﹣36﹣18=54,
故答案为:54;
(3)100×=54(万),
答:全市每天“停课不停学”的学习时间在1~2小时及以上的人数有54万人;
(4)这个调查设计有不合理的地方,如在100万人的总体中,随机抽取的200人作为样本,样本容量偏小,会导致调查的结果不够准确,建议增大样本容量.
18.【解答】解:(1)140÷0.7=200(人)
答:参加本次测试的学生数为200人,
200﹣140﹣36﹣6=18(人),
故答案为:18;
(2)6÷200=0.03,
答:体质健康成绩属于“不及格”等级的频率为0.03;
(3)1800×=1584(人),
答:达到“良好”及以上等级的学生数为1584人.
19.【解答】解:(1)16÷0.08=200,
m=200×0.35=70,n=24÷200=0.12;
故答案为200,70;0.12;
(2)如图,
(3)8000×(0.08+0.2)=2240,
所以该校安全意识不强的学生约有2240人.
10.3《课题学习》
一、选择题
1.想表示某一城市一天中气温变化的情况,一般选用( )
A.条形图 B.扇形图 C.折线图 D.直方图
2.青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?( )
A.100只 B.150只 C.180只 D.200只
3.为鼓励市民珍惜每一滴水,某居委会表扬了100个节约用水模范户,5月份这100户节约用水的情况如下表:
则5月份这100户平均节水的吨数为(精确到0.01吨)( )
A.1.00吨 B.1.15吨 C.1.23吨 D.无法确定
4.某校为了了解九年级学生的体能情况,随机抽查了其中30名学生,测试了他们做1min仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示计算仰卧起坐次数在25~30次的频率是( ).
A.0.1 B.0.2 C.0.3 D.0.4
5.小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
A.各项消费金额占消费总金额的百分比
B.各项消费的金额
C.消费的总金额
D.各项消费金额的增减变化情况
6.为了支援地震灾区同学,某校开展捐书活动,九(1)班40名同学积极参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是( )
A.0.1 B.0.2 C.0.3 D.0.4
二、填空题
7.如图是某校七年一班全班同学1min心跳次数频数直方图,那么,心跳次数在_______之间的学生最多,占统计人数的_____%.(精确到1%)
8.为响应“红歌唱响中国”活动,某乡镇举行了一场“红歌”歌咏比赛,组委会规定:任何一名参赛选手的成绩x满足:60≤x<100,赛后整理所有参赛选手的成绩如下表:
根据表中提供的信息得到n=__________.
9.某中学七年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息可知a的值为__________.
10.七年二班50名同学的一次考试成绩频数分布直方图如图所示,则71~90分之间有____人.
三、解答题
11.已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
12.为了了解学校开展“孝敬父母,从家务事做起”活动的实施情况,该校抽取八年级50名学生调查他们一周(按7天计算)做家务所用时间(单位:小时,调查结果保留一位小数),得到一组数据,并绘制成统计表,请根据表完成下列各_é??_:
(1)填写频率分布表中末完成的部分.
(2)由以上信息判断,每周做家务的时间不超过1.5h的学生所占的百分比是________.
(3)针对以上情况,写一个20字以内倡导“孝敬父母,热爱劳动”的句子.
13.为了进一步了解八年级学生的身体素质情况,体育老师对八年级(1)班50名学生进行1min跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下图所示.
请结合图表完成下列问_é??_.
(1)表中的a=______.
(2)请把频数直方图补充完整.
(3)若八年级学生1min跳绳次数(x)达标要求是:x<120为不合格,120≤x<140为合格,140≤x<160为良,x≥160为优,根据以上信息,请你给学校或八年级同学提一条合理化建议.
14.在某市开展的“体育、艺术2+1”活动中,某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:跳绳这四种运动项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
(1)样本中喜欢B项目的人数百分比是________;
(2)把条形统计图补充完整;
(3)已知该校有1000人,根据样本估计全校喜欢乒乓球的人数是多少?
15.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
(1)填空:a=______,b=________;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165 cm的学生大约有多少人?
参考答案
答案为:C
答案为:D
答案为:B
答案为:D
答案为:A
答案为:B
答案为:59.5~69.5,48;
答案为:0.3
答案为:14
答案为:27
解:(1)计算最大值与最小值的差:32-23=9.
(2)确定组数与组距:已知组距为2,则4.5,因此定为5组.
(3)决定分点,所分的五个小组是:
22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5,30.5~32.5.
(4)列频数分布表:
(5)画频数分布直方图:
解:(1)表格中空缺部分自上而上依次为:0.14,0.06,2.
(2)58%
(3)如:“体验生活,锻炼自我,珍惜母爱,勤奋好学”等.
解:(1)a=12 (2)图略 (3)只要合理即可.
解:(1) 20%
(2) 总人数是44÷44%=100(人),
∴B项目的人数是100×20%=20(人),补图略
(3)1000×44%=440(人),则全校喜欢乒乓球的人数是440人
解:(1) 10 28%
(2)补图略
(3)600×(28%+12%)=240(人),估计身高不低于165 cm的学生大约有240人
