人教版八年级上册 第15章 第2节 分式的化简求值与恒等变形 讲义(无答案)
文档属性
| 名称 | 人教版八年级上册 第15章 第2节 分式的化简求值与恒等变形 讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 20:01:03 | ||
图片预览


文档简介
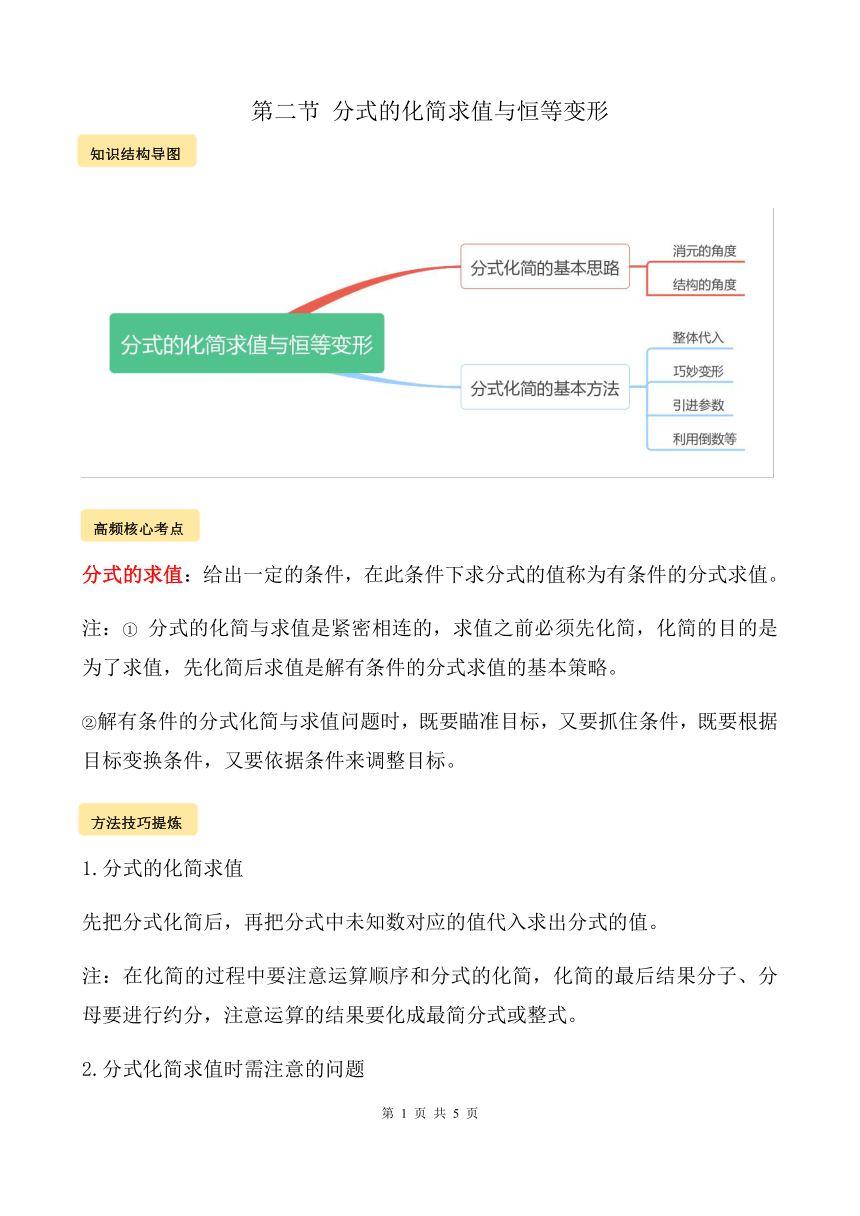
第二节
分式的化简求值与恒等变形
分式的求值:给出一定的条件,在此条件下求分式的值称为有条件的分式求值。
注:①
分式的化简与求值是紧密相连的,求值之前必须先化简,化简的目的是为了求值,先化简后求值是解有条件的分式求值的基本策略。
②解有条件的分式化简与求值问题时,既要瞄准目标,又要抓住条件,既要根据目标变换条件,又要依据条件来调整目标。
1.分式的化简求值
先把分式化简后,再把分式中未知数对应的值代入求出分式的值。
注:在化简的过程中要注意运算顺序和分式的化简,化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式。
2.分式化简求值时需注意的问题
(1)化简求值,一般是先化简为最简分式或整式,再代入求值,化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”。
(2)代入求值时,有直接代入法,整体代入法等常用方法。解题时可根据题目的具体条件选择合适的方法。当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.(注意负数和分数加括号的问题)
3.分式化简求值需要用到下面的一些技巧
⑴适当引入参数;⑵取倒数或利用倒数关系;⑶拆项变形或拆分变形;⑷整体代入;⑸利用比例的性质。
1、已知,则=________。
2、化简:,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值。
3、如果(b+d+f≠0),且a+c+e=3(b+d+f),那么k=________。
4、先化简,再求值:,其中x的值从不等式组的整数解中选取。
5、先化简,再求值:,其中x?+2x-15=0
6、已知=0,求代数式的值。
7、先化简,再求值:(a+2b)(a-2b)+(a+2b)?+(2ab?-8a?b?)÷2ab,其中a=,b=.
日期:_______
姓名:_______
1.若=1,则-1+x=________。
2.如果a-b=,那么代数式的值是(
)
A.-2
B.2
C.
D.
3.当a=时,代数式-2的值为________。
4.若,则的值为________。
5.先化简,再求值:,其中x=3,y=-2.
1.已知x是方程x?+3x-1=0的根,则代数式的值为________。
2.有这样一道题“求-÷的值,其中a=2017”,小马虎不小心把a=2017错抄成a=2007,但他的计算结果是正确的,请说明原因。
3.已知-2a-2=0,求代数式÷的值。
分式的化简求值与恒等变形
分式的求值:给出一定的条件,在此条件下求分式的值称为有条件的分式求值。
注:①
分式的化简与求值是紧密相连的,求值之前必须先化简,化简的目的是为了求值,先化简后求值是解有条件的分式求值的基本策略。
②解有条件的分式化简与求值问题时,既要瞄准目标,又要抓住条件,既要根据目标变换条件,又要依据条件来调整目标。
1.分式的化简求值
先把分式化简后,再把分式中未知数对应的值代入求出分式的值。
注:在化简的过程中要注意运算顺序和分式的化简,化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式。
2.分式化简求值时需注意的问题
(1)化简求值,一般是先化简为最简分式或整式,再代入求值,化简时不能跨度太大,而缺少必要的步骤,代入求值的模式一般为“当…时,原式=…”。
(2)代入求值时,有直接代入法,整体代入法等常用方法。解题时可根据题目的具体条件选择合适的方法。当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.(注意负数和分数加括号的问题)
3.分式化简求值需要用到下面的一些技巧
⑴适当引入参数;⑵取倒数或利用倒数关系;⑶拆项变形或拆分变形;⑷整体代入;⑸利用比例的性质。
1、已知,则=________。
2、化简:,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值。
3、如果(b+d+f≠0),且a+c+e=3(b+d+f),那么k=________。
4、先化简,再求值:,其中x的值从不等式组的整数解中选取。
5、先化简,再求值:,其中x?+2x-15=0
6、已知=0,求代数式的值。
7、先化简,再求值:(a+2b)(a-2b)+(a+2b)?+(2ab?-8a?b?)÷2ab,其中a=,b=.
日期:_______
姓名:_______
1.若=1,则-1+x=________。
2.如果a-b=,那么代数式的值是(
)
A.-2
B.2
C.
D.
3.当a=时,代数式-2的值为________。
4.若,则的值为________。
5.先化简,再求值:,其中x=3,y=-2.
1.已知x是方程x?+3x-1=0的根,则代数式的值为________。
2.有这样一道题“求-÷的值,其中a=2017”,小马虎不小心把a=2017错抄成a=2007,但他的计算结果是正确的,请说明原因。
3.已知-2a-2=0,求代数式÷的值。
