人教版七年级数学下册 5.3.1 平行线的性质 课后练习1(Word版 含答案)
文档属性
| 名称 | 人教版七年级数学下册 5.3.1 平行线的性质 课后练习1(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 813.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 00:00:00 | ||
图片预览


文档简介
人教版七年级数学下册
第五章
相交线与平行线
5.3.1
平行线的性质
课后练习1
一、选择题
1.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③
B.①②④
C.①③④
D.①②③④
2.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A.2个
B.3个
C.4个
D.5个
3.①如图1,AB∥CD,则∠A
+∠E
+∠C=180°;②如图2,AB∥CD,则∠E
=∠A
+∠C;③如图3,AB∥CD,则∠A
+∠E-∠1=180°
;
④如图4,AB∥CD,则∠A=∠C
+∠P.以上结论正确的个数是(
)
A.、1个
B.2个
C.3个
D.4个
4.如图,已知AB∥CD∥EF,则∠、∠、∠三者之间的关系是(
)
A.°
B.°
C.°
D.
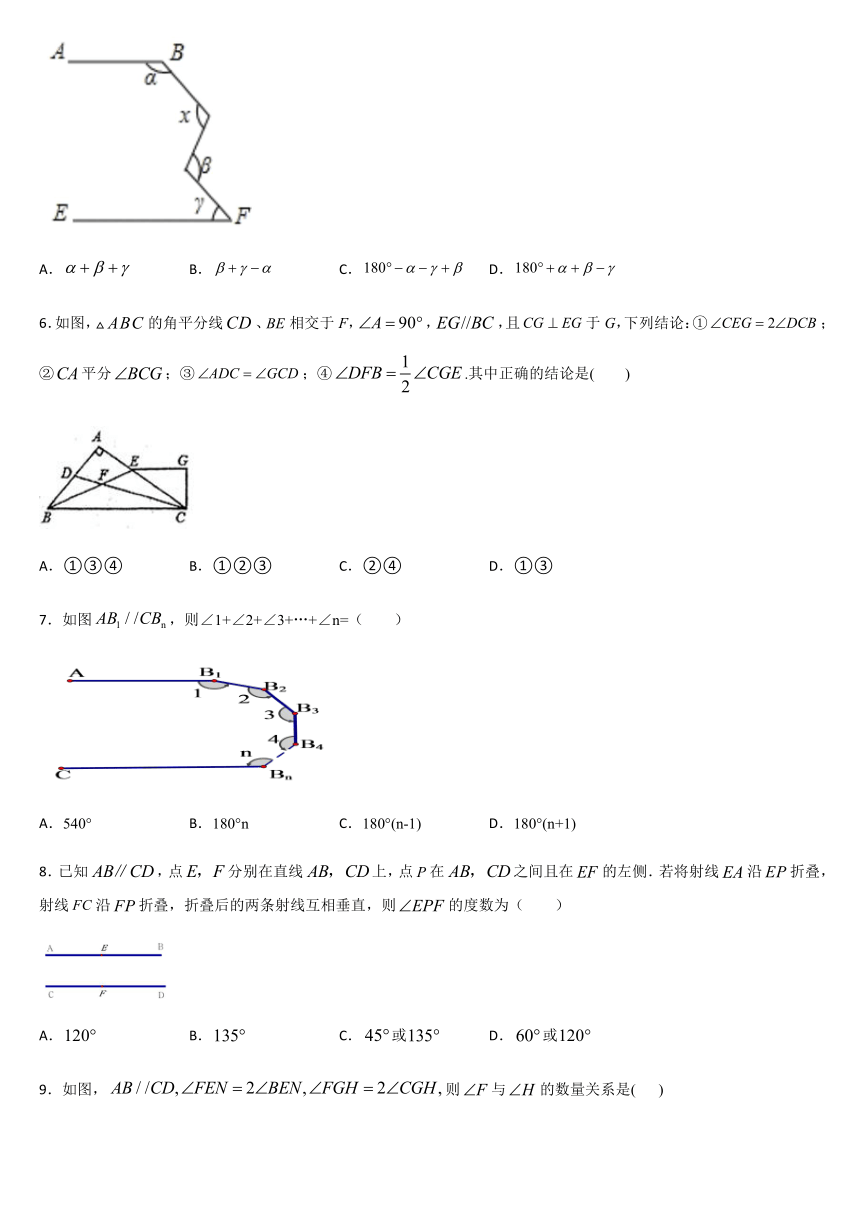
5.如图所示,若AB∥EF,用含、、的式子表示,应为(
)
A.
B.
C.
D.
6.如图,的角平分线、相交于F,,,且于G,下列结论:①;②平分;③;④.其中正确的结论是( )
A.①③④
B.①②③
C.②④
D.①③
7.如图,则∠1+∠2+∠3+…+∠n=(
)
A.540°
B.180°n
C.180°(n-1)
D.180°(n+1)
8.已知,点分别在直线上,点在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为(
)
A.
B.
C.或
D.或
9.如图,则与的数量关系是(
)
A.
B.
C.
D.
10.如图,,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得,作的角平分线交BH于点G,若,则的度数是(
)
A.
B.
C.
D.
二、填空题
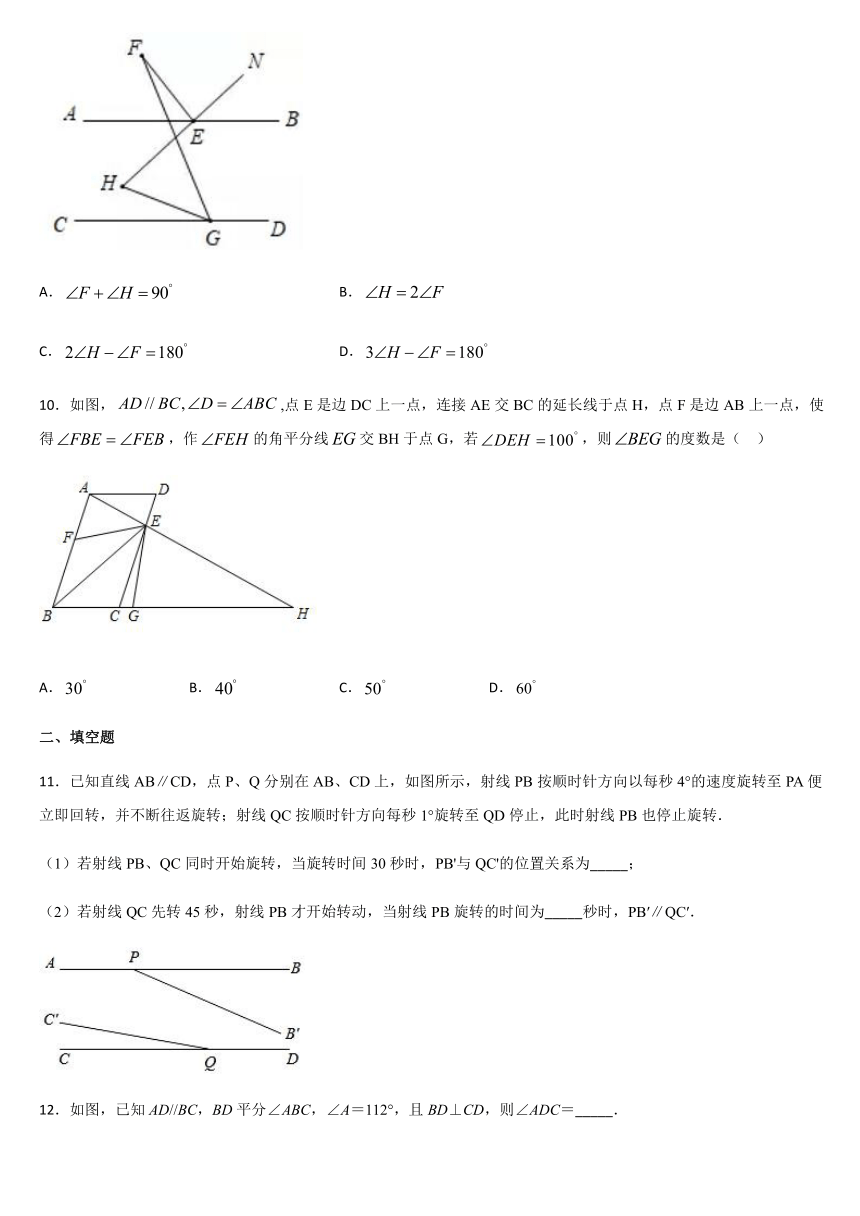
11.已知直线AB∥CD,点P、Q分别在AB、CD上,如图所示,射线PB按顺时针方向以每秒4°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按顺时针方向每秒1°旋转至QD停止,此时射线PB也停止旋转.
(1)若射线PB、QC同时开始旋转,当旋转时间30秒时,PB'与QC'的位置关系为_____;
(2)若射线QC先转45秒,射线PB才开始转动,当射线PB旋转的时间为_____秒时,PB′∥QC′.
12.如图,已知AD//BC,BD平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC=_____.
13.如图,已知A1BAnC,则∠A1+∠A2+…+∠An等于__________(用含n的式子表示).
14.如图,已知AB∥CD,点E,F分别在直线AB,CD上点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线互相垂直,则EPF的度数为
_____.
15.如图,
已知,,,则_________
三、解答题
16.已知两条直线l1,l2,l1∥l2,点A,B在直线l1上,点A在点B的左边,点C,D在直线l2上,且满足.
(1)如图①,求证:AD∥BC;
(2)点M,N在线段CD上,点M在点N的左边且满足,且AN平分∠CAD;
(Ⅰ)如图②,当时,求∠DAM的度数;
(Ⅱ)如图③,当时,求∠ACD的度数.
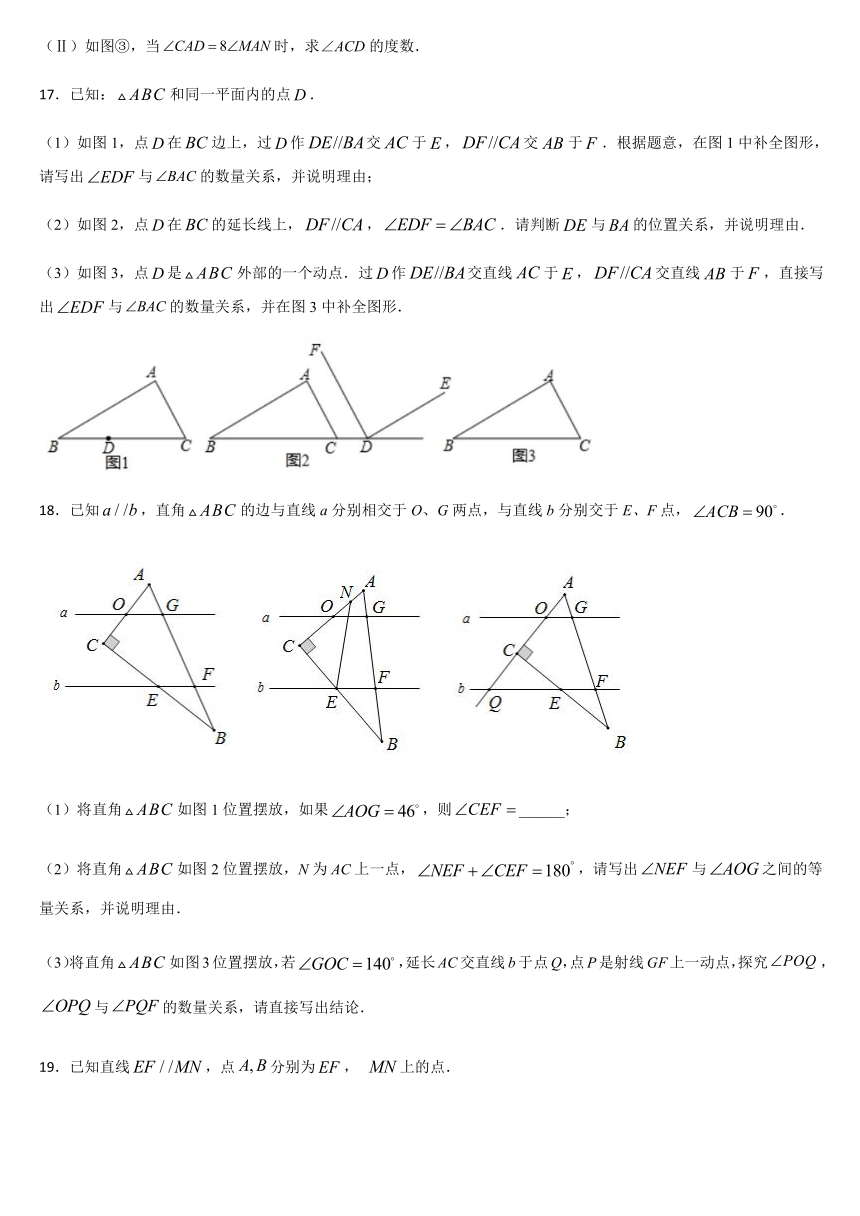
17.已知:和同一平面内的点.
(1)如图1,点在边上,过作交于,交于.根据题意,在图1中补全图形,请写出与的数量关系,并说明理由;
(2)如图2,点在的延长线上,,.请判断与的位置关系,并说明理由.
(3)如图3,点是外部的一个动点.过作交直线于,交直线于,直接写出与的数量关系,并在图3中补全图形.
18.已知,直角的边与直线a分别相交于O、G两点,与直线b分别交于E、F点,.
(1)将直角如图1位置摆放,如果,则______;
(2)将直角如图2位置摆放,N为AC上一点,,请写出与之间的等量关系,并说明理由.
(3)将直角如图3位置摆放,若,延长AC交直线b于点Q,点P是射线GF上一动点,探究,与的数量关系,请直接写出结论.
19.已知直线,点分别为,
上的点.
(1)如图1,若,,
,求与的度数;
(2)如图2,若,,
,则_________;
(3)若把(2)中“,,
”改为“,,
”,则_________.(用含的式子表示)
20.如图1,D是△ABC延长线上的一点,CEAB.
(1)求证:∠ACD=∠A+∠B;
(2)如图2,过点A作BC的平行线交CE于点H,CF平分∠ECD,FA平分∠HAD,若∠BAD=70°,求∠F的度数.
(3)如图3,AHBD,G为CD上一点,Q为AC上一点,GR平分∠QGD交AH于R,QN平分∠AQG交AH于N,QMGR,猜想∠MQN与∠ACB的关系,说明理由.
21.如图,两个形状,大小完全相同的含有30°、60°的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
(1)①如图1,∠DPC=
度.
②我们规定,如果两个三角形只要有一组边平行,我们就称这两个三角形为“孪生三角形”,如图1,三角板BPD不动,三角板PAC从图示位置开始每秒10°逆时针旋转一周(0°旋转360°),问旋转时间t为多少时,这两个三角形是“孪生三角形”.
(2)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速2°/秒,在两个三角板旋转过程中,(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,以下两个结论:①为定值;②∠BPN+∠CPD为定值,请选择你认为对的结论加以证明.
22.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
23.(1)如图所示,,且点在射线与之间,请说明的理由.
(2)现在如图所示,仍有,但点在与的上方,
①请尝试探索,,三者的数量关系.
②请说明理由.
【参考答案】
1.D
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.D
10.B
11.PB′⊥QC′
15秒或63秒或135秒.
12.124°
13.
14.45°或135°
15.90°
16.(1),
,
又,
,
;
(2)(Ⅰ),
,
,
,
由(1)已得:,
,
;
(Ⅱ)设,则,
平分,
,
,
,
,
由(1)已得:,
,即,
解得,
,
又,
.
17.(1)由题意,补全图形如下:
,理由如下:
,
,
,
,
;
(2),理由如下:
如图,延长BA交DF于点O,
,
,
,
,
;
(3)由题意,有以下两种情况:
①如图3-1,,理由如下:
,
,
,
,
,
由对顶角相等得:,
;
②如图3-2,,理由如下:
,
,
,
,
.
18.解:(1)如图1,作CP∥a,
∵,
∴CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°,
故答案为136°;
(2)∠AOG+∠NEF=90°.
理由如下:如图2,作CP∥a,
则CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
而∠NEF+∠CEF=180°,
∴∠BCP=∠NEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+∠NEF=90°;
(3)如图3,当点P在GF上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF;
如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∵∠OPN=∠OPQ+∠QPN,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
19.解:(1)如图示,分别过点作,,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,,
∴.
(2)如图示,分别过点作,,
∵,∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,,
∴.
故答案为:160;
(3)同理(1)的求法
∵,∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,
,
∴.
故答案为:.
20.解:(1)∵CEAB,
∴∠ACE=∠A,∠ECD=∠B,
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B;
(2)∵CF平分∠ECD,FA平分∠HAD,
∴∠FCD=∠ECD,∠HAF=∠HAD,
∴∠F=∠HAD+∠ECD=(∠HAD+∠ECD),
∵CHAB,
∴∠ECD=∠B,
∵AHBC,
∴∠B+∠HAB=180°,
∵∠BAD=70°,
,
∴∠F=(∠B+∠HAD)=55°;
(3)∠MQN=∠ACB,理由如下:
平分,
.
平分,
.
,
.
∴∠MQN=∠MQG﹣∠NQG
=180°﹣∠QGR﹣∠NQG
=180°﹣(∠AQG+∠QGD)
=180°﹣(180°﹣∠CQG+180°﹣∠QGC)
=(∠CQG+∠QGC)
=∠ACB.
21.解:(1)①∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180﹣30﹣60=90°,
故答案为90;
②如图1﹣1,当BD∥PC时,
∵PC∥BD,∠DBP=90°,
∴∠CPN=∠DBP=90°,
∵∠CPA=60°,
∴∠APN=30°,
∵转速为10°/秒,
∴旋转时间为3秒;
如图1﹣2,当PC∥BD时,
∵∠PBD=90°,
∴∠CPB=∠DBP=90°,
∵∠CPA=60°,
∴∠APM=30°,
∵三角板PAC绕点P逆时针旋转的角度为180°+30°=210°,
∵转速为10°/秒,
∴旋转时间为21秒,
如图1﹣3,当PA∥BD时,即点D与点C重合,此时∠ACP=∠BPD=30°,则AC∥BP,
∵PA∥BD,
∴∠DBP=∠APN=90°,
∴三角板PAC绕点P逆时针旋转的角度为90°,
∵转速为10°/秒,
∴旋转时间为9秒,
如图1﹣4,当PA∥BD时,
∵∠DPB=∠ACP=30°,
∴AC∥BP,
∵PA∥BD,
∴∠DBP=∠BPA=90°,
∴三角板PAC绕点P逆时针旋转的角度为90°+180°=270°,
∵转速为10°/秒,
∴旋转时间为27秒,
如图1﹣5,当AC∥DP时,
∵AC∥DP,
∴∠C=∠DPC=30°,
∴∠APN=180°﹣30°﹣30°﹣60°=60°,
∴三角板PAC绕点P逆时针旋转的角度为60°,
∵转速为10°/秒,
∴旋转时间为6秒,
如图1﹣6,当时,
∴三角板PAC绕点P逆时针旋转的角度为
∵转速为10°/秒,
∴旋转时间为秒,
如图1﹣7,当AC∥BD时,
∵AC∥BD,
∴∠DBP=∠BAC=90°,
∴点A在MN上,
∴三角板PAC绕点P逆时针旋转的角度为180°,
∵转速为10°/秒,
∴旋转时间为18秒,
当时,如图1-3,1-4,旋转时间分别为:,
综上所述:当t为或或或或或或时,这两个三角形是“孪生三角形”;
(2)如图,当在上方时,
①正确,
理由如下:设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180°﹣2t,∠DPM=30°﹣2t,∠APN=3t.
∴∠CPD=180°﹣∠DPM﹣∠CPA﹣∠APN=90°﹣t,
∴
②∠BPN+∠CPD=180°﹣2t+90°﹣t=270°﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.
当在下方时,如图,
①正确,
理由如下:设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180°﹣2t,∠DPM=
∠APN=3t.
∴∠CPD=
∴
②∠BPN+∠CPD=180°﹣2t+90°﹣t=270°﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.
综上:①正确,②错误.
22.解:(1)证明:AD∥BC,
∠ADC+∠BCD=180°,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°;
(2)解:∵∠FBD+∠BDE=90°-∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°.
23.解:(1)过点E作EF∥AB,
∴∠A=∠AEF,
∵AB∥CD,
∴EF∥CD,
∴∠FEC=∠C,
∵∠AEC=∠AEF+∠FEC,
∴∠AEC=∠A+∠C;
(2)①∠1+∠2-∠E=180°,
②过点E作EF∥AB,
∴∠AEF+∠1=180°,
∵AB∥CD,
∴EF∥CD,
∴∠FEC=∠2,
即∠CEA+∠AEF=∠2,
∴∠AEF=∠2-∠CEA,
∴∠2-∠CEA+∠1=180°,
即∠1+∠2-∠AEC=180°.
第五章
相交线与平行线
5.3.1
平行线的性质
课后练习1
一、选择题
1.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③
B.①②④
C.①③④
D.①②③④
2.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A.2个
B.3个
C.4个
D.5个
3.①如图1,AB∥CD,则∠A
+∠E
+∠C=180°;②如图2,AB∥CD,则∠E
=∠A
+∠C;③如图3,AB∥CD,则∠A
+∠E-∠1=180°
;
④如图4,AB∥CD,则∠A=∠C
+∠P.以上结论正确的个数是(
)
A.、1个
B.2个
C.3个
D.4个
4.如图,已知AB∥CD∥EF,则∠、∠、∠三者之间的关系是(
)
A.°
B.°
C.°
D.
5.如图所示,若AB∥EF,用含、、的式子表示,应为(
)
A.
B.
C.
D.
6.如图,的角平分线、相交于F,,,且于G,下列结论:①;②平分;③;④.其中正确的结论是( )
A.①③④
B.①②③
C.②④
D.①③
7.如图,则∠1+∠2+∠3+…+∠n=(
)
A.540°
B.180°n
C.180°(n-1)
D.180°(n+1)
8.已知,点分别在直线上,点在之间且在的左侧.若将射线沿折叠,射线沿折叠,折叠后的两条射线互相垂直,则的度数为(
)
A.
B.
C.或
D.或
9.如图,则与的数量关系是(
)
A.
B.
C.
D.
10.如图,,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得,作的角平分线交BH于点G,若,则的度数是(
)
A.
B.
C.
D.
二、填空题
11.已知直线AB∥CD,点P、Q分别在AB、CD上,如图所示,射线PB按顺时针方向以每秒4°的速度旋转至PA便立即回转,并不断往返旋转;射线QC按顺时针方向每秒1°旋转至QD停止,此时射线PB也停止旋转.
(1)若射线PB、QC同时开始旋转,当旋转时间30秒时,PB'与QC'的位置关系为_____;
(2)若射线QC先转45秒,射线PB才开始转动,当射线PB旋转的时间为_____秒时,PB′∥QC′.
12.如图,已知AD//BC,BD平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC=_____.
13.如图,已知A1BAnC,则∠A1+∠A2+…+∠An等于__________(用含n的式子表示).
14.如图,已知AB∥CD,点E,F分别在直线AB,CD上点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线互相垂直,则EPF的度数为
_____.
15.如图,
已知,,,则_________
三、解答题
16.已知两条直线l1,l2,l1∥l2,点A,B在直线l1上,点A在点B的左边,点C,D在直线l2上,且满足.
(1)如图①,求证:AD∥BC;
(2)点M,N在线段CD上,点M在点N的左边且满足,且AN平分∠CAD;
(Ⅰ)如图②,当时,求∠DAM的度数;
(Ⅱ)如图③,当时,求∠ACD的度数.
17.已知:和同一平面内的点.
(1)如图1,点在边上,过作交于,交于.根据题意,在图1中补全图形,请写出与的数量关系,并说明理由;
(2)如图2,点在的延长线上,,.请判断与的位置关系,并说明理由.
(3)如图3,点是外部的一个动点.过作交直线于,交直线于,直接写出与的数量关系,并在图3中补全图形.
18.已知,直角的边与直线a分别相交于O、G两点,与直线b分别交于E、F点,.
(1)将直角如图1位置摆放,如果,则______;
(2)将直角如图2位置摆放,N为AC上一点,,请写出与之间的等量关系,并说明理由.
(3)将直角如图3位置摆放,若,延长AC交直线b于点Q,点P是射线GF上一动点,探究,与的数量关系,请直接写出结论.
19.已知直线,点分别为,
上的点.
(1)如图1,若,,
,求与的度数;
(2)如图2,若,,
,则_________;
(3)若把(2)中“,,
”改为“,,
”,则_________.(用含的式子表示)
20.如图1,D是△ABC延长线上的一点,CEAB.
(1)求证:∠ACD=∠A+∠B;
(2)如图2,过点A作BC的平行线交CE于点H,CF平分∠ECD,FA平分∠HAD,若∠BAD=70°,求∠F的度数.
(3)如图3,AHBD,G为CD上一点,Q为AC上一点,GR平分∠QGD交AH于R,QN平分∠AQG交AH于N,QMGR,猜想∠MQN与∠ACB的关系,说明理由.
21.如图,两个形状,大小完全相同的含有30°、60°的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
(1)①如图1,∠DPC=
度.
②我们规定,如果两个三角形只要有一组边平行,我们就称这两个三角形为“孪生三角形”,如图1,三角板BPD不动,三角板PAC从图示位置开始每秒10°逆时针旋转一周(0°旋转360°),问旋转时间t为多少时,这两个三角形是“孪生三角形”.
(2)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速2°/秒,在两个三角板旋转过程中,(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,以下两个结论:①为定值;②∠BPN+∠CPD为定值,请选择你认为对的结论加以证明.
22.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
23.(1)如图所示,,且点在射线与之间,请说明的理由.
(2)现在如图所示,仍有,但点在与的上方,
①请尝试探索,,三者的数量关系.
②请说明理由.
【参考答案】
1.D
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.D
10.B
11.PB′⊥QC′
15秒或63秒或135秒.
12.124°
13.
14.45°或135°
15.90°
16.(1),
,
又,
,
;
(2)(Ⅰ),
,
,
,
由(1)已得:,
,
;
(Ⅱ)设,则,
平分,
,
,
,
,
由(1)已得:,
,即,
解得,
,
又,
.
17.(1)由题意,补全图形如下:
,理由如下:
,
,
,
,
;
(2),理由如下:
如图,延长BA交DF于点O,
,
,
,
,
;
(3)由题意,有以下两种情况:
①如图3-1,,理由如下:
,
,
,
,
,
由对顶角相等得:,
;
②如图3-2,,理由如下:
,
,
,
,
.
18.解:(1)如图1,作CP∥a,
∵,
∴CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
∴∠BCP=180°﹣∠CEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+180°﹣∠CEF=90°,
∵∠AOG=46°,
∴∠CEF=136°,
故答案为136°;
(2)∠AOG+∠NEF=90°.
理由如下:如图2,作CP∥a,
则CP∥a∥b,
∴∠AOG=∠ACP,∠BCP+∠CEF=180°,
而∠NEF+∠CEF=180°,
∴∠BCP=∠NEF,
∵∠ACP+∠BCP=90°,
∴∠AOG+∠NEF=90°;
(3)如图3,当点P在GF上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∴∠OPQ=∠GOP+∠PQF,
∴∠OPQ=140°﹣∠POQ+∠PQF;
如图4,当点P在线段GF的延长线上时,过点P作PN∥OG,
∴NP∥OG∥EF,
∴∠GOP=∠OPN,∠PQF=∠NPQ,
∵∠OPN=∠OPQ+∠QPN,
∴∠GOP=∠OPQ+∠PQF,
∴140°﹣∠POQ=∠OPQ+∠PQF.
19.解:(1)如图示,分别过点作,,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,,
∴.
(2)如图示,分别过点作,,
∵,∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,,
∴.
故答案为:160;
(3)同理(1)的求法
∵,∴,
∴,
∴,
∴,
∵,
∴,
又∵,
∴,
,
∴.
故答案为:.
20.解:(1)∵CEAB,
∴∠ACE=∠A,∠ECD=∠B,
∵∠ACD=∠ACE+∠ECD,
∴∠ACD=∠A+∠B;
(2)∵CF平分∠ECD,FA平分∠HAD,
∴∠FCD=∠ECD,∠HAF=∠HAD,
∴∠F=∠HAD+∠ECD=(∠HAD+∠ECD),
∵CHAB,
∴∠ECD=∠B,
∵AHBC,
∴∠B+∠HAB=180°,
∵∠BAD=70°,
,
∴∠F=(∠B+∠HAD)=55°;
(3)∠MQN=∠ACB,理由如下:
平分,
.
平分,
.
,
.
∴∠MQN=∠MQG﹣∠NQG
=180°﹣∠QGR﹣∠NQG
=180°﹣(∠AQG+∠QGD)
=180°﹣(180°﹣∠CQG+180°﹣∠QGC)
=(∠CQG+∠QGC)
=∠ACB.
21.解:(1)①∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180﹣30﹣60=90°,
故答案为90;
②如图1﹣1,当BD∥PC时,
∵PC∥BD,∠DBP=90°,
∴∠CPN=∠DBP=90°,
∵∠CPA=60°,
∴∠APN=30°,
∵转速为10°/秒,
∴旋转时间为3秒;
如图1﹣2,当PC∥BD时,
∵∠PBD=90°,
∴∠CPB=∠DBP=90°,
∵∠CPA=60°,
∴∠APM=30°,
∵三角板PAC绕点P逆时针旋转的角度为180°+30°=210°,
∵转速为10°/秒,
∴旋转时间为21秒,
如图1﹣3,当PA∥BD时,即点D与点C重合,此时∠ACP=∠BPD=30°,则AC∥BP,
∵PA∥BD,
∴∠DBP=∠APN=90°,
∴三角板PAC绕点P逆时针旋转的角度为90°,
∵转速为10°/秒,
∴旋转时间为9秒,
如图1﹣4,当PA∥BD时,
∵∠DPB=∠ACP=30°,
∴AC∥BP,
∵PA∥BD,
∴∠DBP=∠BPA=90°,
∴三角板PAC绕点P逆时针旋转的角度为90°+180°=270°,
∵转速为10°/秒,
∴旋转时间为27秒,
如图1﹣5,当AC∥DP时,
∵AC∥DP,
∴∠C=∠DPC=30°,
∴∠APN=180°﹣30°﹣30°﹣60°=60°,
∴三角板PAC绕点P逆时针旋转的角度为60°,
∵转速为10°/秒,
∴旋转时间为6秒,
如图1﹣6,当时,
∴三角板PAC绕点P逆时针旋转的角度为
∵转速为10°/秒,
∴旋转时间为秒,
如图1﹣7,当AC∥BD时,
∵AC∥BD,
∴∠DBP=∠BAC=90°,
∴点A在MN上,
∴三角板PAC绕点P逆时针旋转的角度为180°,
∵转速为10°/秒,
∴旋转时间为18秒,
当时,如图1-3,1-4,旋转时间分别为:,
综上所述:当t为或或或或或或时,这两个三角形是“孪生三角形”;
(2)如图,当在上方时,
①正确,
理由如下:设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180°﹣2t,∠DPM=30°﹣2t,∠APN=3t.
∴∠CPD=180°﹣∠DPM﹣∠CPA﹣∠APN=90°﹣t,
∴
②∠BPN+∠CPD=180°﹣2t+90°﹣t=270°﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.
当在下方时,如图,
①正确,
理由如下:设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180°﹣2t,∠DPM=
∠APN=3t.
∴∠CPD=
∴
②∠BPN+∠CPD=180°﹣2t+90°﹣t=270°﹣3t,可以看出∠BPN+∠CPD随着时间在变化,不为定值,结论错误.
综上:①正确,②错误.
22.解:(1)证明:AD∥BC,
∠ADC+∠BCD=180°,
∵DE平分∠ADB,∠BDC=∠BCD,
∴∠ADE=∠EDB,∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°;
(2)解:∵∠FBD+∠BDE=90°-∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°.
23.解:(1)过点E作EF∥AB,
∴∠A=∠AEF,
∵AB∥CD,
∴EF∥CD,
∴∠FEC=∠C,
∵∠AEC=∠AEF+∠FEC,
∴∠AEC=∠A+∠C;
(2)①∠1+∠2-∠E=180°,
②过点E作EF∥AB,
∴∠AEF+∠1=180°,
∵AB∥CD,
∴EF∥CD,
∴∠FEC=∠2,
即∠CEA+∠AEF=∠2,
∴∠AEF=∠2-∠CEA,
∴∠2-∠CEA+∠1=180°,
即∠1+∠2-∠AEC=180°.
