2020-2021学年陕西省榆林市高二上学期期末数学试卷(理科) (Word解析版)
文档属性
| 名称 | 2020-2021学年陕西省榆林市高二上学期期末数学试卷(理科) (Word解析版) | 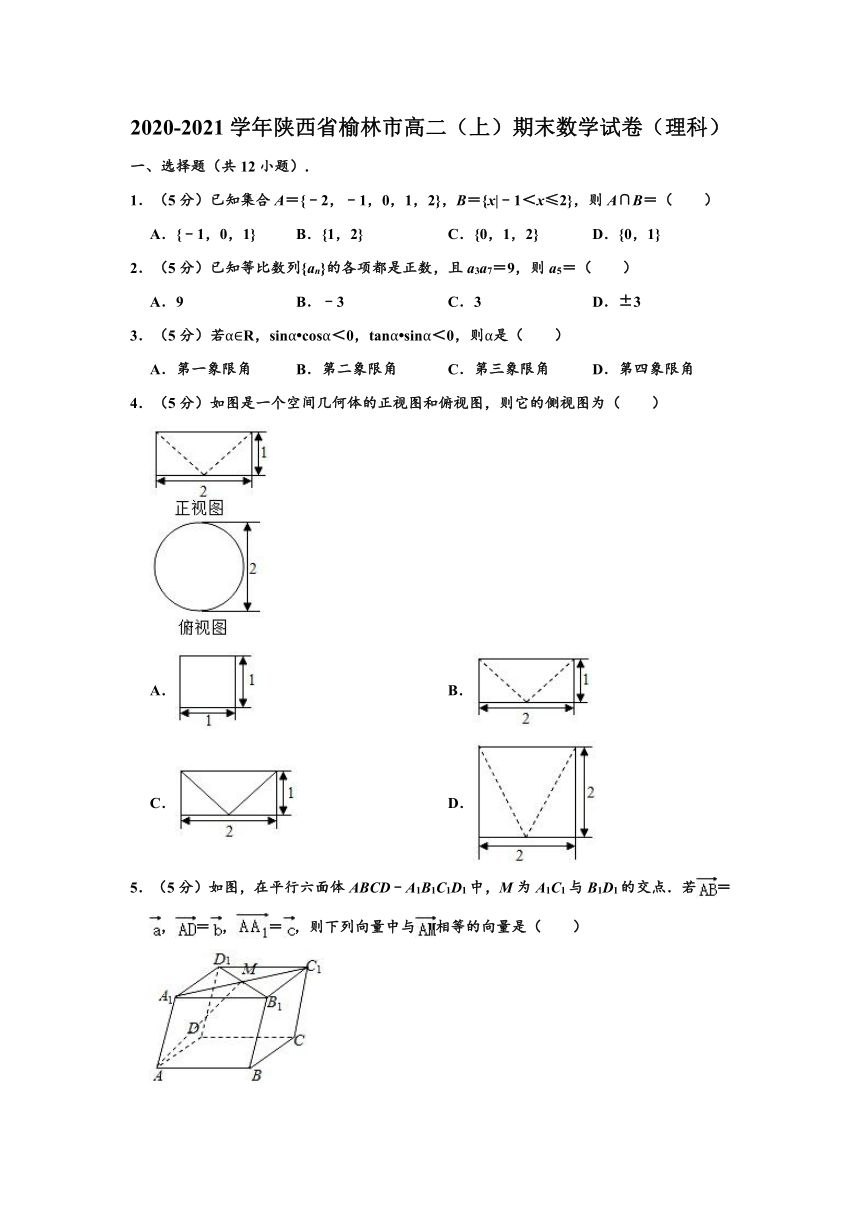 | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 21:36:24 | ||
图片预览





文档简介
2020-2021学年陕西省榆林市高二(上)期末数学试卷(理科)
一、选择题(共12小题).
1.(5分)已知集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},则A∩B=( )
A.{﹣1,0,1} B.{1,2} C.{0,1,2} D.{0,1}
2.(5分)已知等比数列{an}的各项都是正数,且a3a7=9,则a5=( )
A.9 B.﹣3 C.3 D.±3
3.(5分)若α∈R,sinα?cosα<0,tanα?sinα<0,则α是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
4.(5分)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A. B.
C. D.
5.(5分)如图,在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若=,=,=,则下列向量中与相等的向量是( )
A.﹣++ B. C.﹣﹣+ D.
6.(5分)已知x<﹣1,那么在下列不等式中,不成立的是( )
A.x2﹣1>0 B. C.sinx﹣x>0 D.cosx+x>0
7.(5分)已知直线l?平面α,则“直线m⊥平面α”是“m⊥l”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.(5分)已知过点M(2,﹣4)的直线l与圆C:(x﹣1)2+(y+2)2=5相切,且与直线m:ax﹣2y+3=0垂直,则实数a的值为( )
A.4 B.2 C.﹣2 D.﹣4
9.(5分)已知函数f(x)=ax2﹣x(a≠0),若对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,则实数a的取值范围是( )
A. B. C. D.
10.(5分)边长为4的正方形ABCD的四个顶点都在球O上,OA与平面ABCD所成角为,则球O的表面积为( )
A.64π B.32π C.16π D.128π
11.(5分)已知是一个等差数列的前n项和,对于函数f(x)=x2﹣ax,若数列的前n项和为Tn,则T2020的值为( )
A. B. C. D.
12.(5分)已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+∞) D.(2,+∞)
二、填空题(共4小题).
13.(5分)已知向量、不共线,,,若,则实数m= .
14.(5分)某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为 .
15.(5分)为了净化水质,向一游泳池加入某种药品,加药后,池水中该药品的浓度C(单位:mg/L)随时间t(单位:h)的变化关系为,则池水中药品的浓度最大可达到 mg/L.
16.(5分)已知函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)的图象,现有如下命题:
p1:函数g(x)的最小正周期是2π;
p2:函数g(x)在区间上单调递增;
p3:函数g(x)在区间上的值域为[﹣1,2].
则下述命题中所有真命题的序号是 .
①(¬p2)∧p3;②p1∨(¬p3);③p2∨p3;④p1∧p2.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(Ⅰ)解不等式;
(Ⅱ)已知函数f(x)=mx2﹣mx﹣1(m≠0),若f(x)<0对于一切实数x都成立,求m的取值范围.
18.(12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(1)求an;
(2)设,证明数列{bn}是等比数列,并求其前n项和Tn.
19.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2A+sin2C﹣sin2B=sinAsinC,c=2.
(1)求sinB的值;
(2)设D在BC边上,且BD=AD=2DC,求△ABC的面积.
20.(12分)为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,各类商贩所占比例如图1.
(1)该市城管委为了更好地服务百姓,打算从流动商贩经营点中随机抽取100个进行政策问询.如果按照分层抽样的方式随机抽取,请问应抽取小吃类、果蔬类商贩各多少家?
(2)为了更好地了解商户的收入情况,工作人员还对某果蔬经营点最近40天的日收入进行了统计(单位:元),所得频率分布直方图如图2.
(ⅰ)请根据频率分布直方图估计该果蔬经营点的日平均收入(同一组中的数据用该组区间的中点值为代表);
(ⅱ)若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
21.(12分)已知椭圆的离心率为,抛物线C2的焦点与椭圆C1的右焦点F重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点.
(1)求的值;
(2)设M为C1与C2的公共点,若,求C1与C2的标准方程.
22.(12分)如图,四边形ABCD与四边形BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(Ⅰ)求证:平面ACF⊥平面ABCD;
(Ⅱ)求二面角A﹣FC﹣B的余弦值.
参考答案
一、选择题(共12小题).
1.(5分)已知集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},则A∩B=( )
A.{﹣1,0,1} B.{1,2} C.{0,1,2} D.{0,1}
解:集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},
则A∩B={0,1,2}.
故选:C.
2.(5分)已知等比数列{an}的各项都是正数,且a3a7=9,则a5=( )
A.9 B.﹣3 C.3 D.±3
解:等比数列{an}的各项都是正数,且a3a7=9,则a52=a3a7=9,
∴a5=3,
故选:C.
3.(5分)若α∈R,sinα?cosα<0,tanα?sinα<0,则α是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
解:∵sinα?cosα<0,
∴α在第二四象限,
∵tanα?sinα<0,
∴α在第二三象限,
故α的终边在第二象限,
故选:B.
4.(5分)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A. B.
C. D.
解:由已知中的空间几何体的正视图和俯视图可得:
该几何体是一个底面半径为1,高为1的圆柱挖去一个同底等高的圆锥所得的组合体,
故其侧视图为:
故选:B.
5.(5分)如图,在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若=,=,=,则下列向量中与相等的向量是( )
A.﹣++ B. C.﹣﹣+ D.
解:=+=+=+(+)=+(+),
故选:B.
6.(5分)已知x<﹣1,那么在下列不等式中,不成立的是( )
A.x2﹣1>0 B. C.sinx﹣x>0 D.cosx+x>0
解:∵x<﹣1,∴x2﹣1>0,x+<﹣2,
又∵sinx,cosx∈[﹣1,1],
∴sinx﹣x>0,cosx+x<0.
可得:ABC成立,D不成立.
故选:D.
7.(5分)已知直线l?平面α,则“直线m⊥平面α”是“m⊥l”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:若直线m垂直于平面α,则直线m必垂直平面内的直线l,
但直线m要垂直于平面α,则m要垂直于平面α内的两条相交直线,故m⊥l无法推知直线m⊥平面α,
故“直线m⊥平面α”是“m⊥l”的充分不必要条件,
故选:A.
8.(5分)已知过点M(2,﹣4)的直线l与圆C:(x﹣1)2+(y+2)2=5相切,且与直线m:ax﹣2y+3=0垂直,则实数a的值为( )
A.4 B.2 C.﹣2 D.﹣4
解:根据题意,圆C:(x﹣1)2+(y+2)2=5,圆心C(1,﹣2),
而点M(2,﹣4),则有(2﹣1)2+(﹣4+2)2=5,则点M在圆C上,
若过点M的切线与直线m:ax﹣2y+3=0垂直,则直线CM与直线m平行,
而直线MC的斜率k==﹣2,
则有=﹣2,则a=﹣4,
故选:D.
9.(5分)已知函数f(x)=ax2﹣x(a≠0),若对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,则实数a的取值范围是( )
A. B. C. D.
解:因为f(x)=ax2﹣x对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,
所以f(x1)﹣f(x2)<0即f(x1)<f(x2),
所以f(x)在[2,+∞)上单调递增,
,解得,a.
故选:C.
10.(5分)边长为4的正方形ABCD的四个顶点都在球O上,OA与平面ABCD所成角为,则球O的表面积为( )
A.64π B.32π C.16π D.128π
解:如图,设正方形ABCD外接圆的圆心为O1,由题意,,则,表面积S=4π?42=64π.
故选:A.
11.(5分)已知是一个等差数列的前n项和,对于函数f(x)=x2﹣ax,若数列的前n项和为Tn,则T2020的值为( )
A. B. C. D.
解:是一个等差数列的前n项和,
可得a+1=0,解得a=﹣1,
所以函数f(x)=x2+x,
数列即,=,
所以数列的前n项和为Tn==1﹣,
则T2020=1﹣=.
故选:D.
12.(5分)已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+∞) D.(2,+∞)
解:已知双曲线的右焦点为F,
若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,
则该直线的斜率的绝对值小于等于渐近线的斜率,
∴≥,离心率e2=,
∴e≥2,
故选:C.
二、填空题(本大题共4小题,每小题5分,共20分)
13.(5分)已知向量、不共线,,,若,则实数m= ﹣3 .
解:向量、不共线,,,
若,则m﹣3(m+2)=0,
解得m=﹣3.
故答案为:﹣3.
14.(5分)某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为 0.39 .
解:某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,
其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,
则不中奖的概率为P=1﹣0.05﹣0.16﹣0.40=0.39.
故答案为:0.39.
15.(5分)为了净化水质,向一游泳池加入某种药品,加药后,池水中该药品的浓度C(单位:mg/L)随时间t(单位:h)的变化关系为,则池水中药品的浓度最大可达到 4 mg/L.
解:∵t>0,
∴==4,当且仅当t=即t=3时,等号成立,
∴池水中药品的浓度最大可达到4mg/L.
故答案为:4.
16.(5分)已知函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)的图象,现有如下命题:
p1:函数g(x)的最小正周期是2π;
p2:函数g(x)在区间上单调递增;
p3:函数g(x)在区间上的值域为[﹣1,2].
则下述命题中所有真命题的序号是 ①③ .
①(¬p2)∧p3;②p1∨(¬p3);③p2∨p3;④p1∧p2.
解:函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)=2sin(2x﹣)的图象,
所以:A:函数的最小正周期为π,故p1为假命题,
B:当时,故,所以函数的图象先减后增,故p2为假命题;¬p2为真命题;
C:当时,所以,则g(x)∈[﹣1,2],故p3为真命题;¬p3为假命题;
所以:①(¬p2)∧p3为真命题;②p1∨(¬p3)为假命题;③p2∨p3为真命题;④p1∧p2为假命题;
故答案为:①③.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(Ⅰ)解不等式;
(Ⅱ)已知函数f(x)=mx2﹣mx﹣1(m≠0),若f(x)<0对于一切实数x都成立,求m的取值范围.
解:(Ⅰ)根据题意,不等式可转化成不等式(2x﹣5)(x﹣3)≥0,但x≠3,
解得x>3或,
故原不等式的解集为;
(Ⅱ)根据题意,由于m≠0,f(x)=mx2﹣mx﹣1<0对于一切实数x都成立,
则有,解之得﹣4<m<0,
故m的取值范围是(﹣4,0).
18.(12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(1)求an;
(2)设,证明数列{bn}是等比数列,并求其前n项和Tn.
【解答】解(1)根据题意,{an}是等差数列,
若S7=14,a2+a12=10,则有S7=7a1+21d=14,a2+a12=2a1+12d=10,
联立解得a1=﹣1,d=1,
所以an=n﹣2;
(2)证明:由=2n﹣2,则,
故列{bn}是首项为,公比为2的等比数列.
数列{bn}的前n项和.
19.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2A+sin2C﹣sin2B=sinAsinC,c=2.
(1)求sinB的值;
(2)设D在BC边上,且BD=AD=2DC,求△ABC的面积.
解:(1)△ABC中,sin2A+sin2C﹣sin2B=sinAsinC,
由正弦定理得,a2+c2﹣b2=ac,
所以cosB===;
又B∈(0,π),
所以sinB===;
(2)如图所示,
设BD=AD=2DC=x,由c=AB=2,
利用余弦定理得,AD2=AB2+BD2﹣2AB?BD?cosB,
即x2=22+x2﹣2×2×x×,
解得x=3,CD=x=,
所以△ABC的面积为
S△ABC=AB?BC?sinB=×2×(3+)×=3.
20.(12分)为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,各类商贩所占比例如图1.
(1)该市城管委为了更好地服务百姓,打算从流动商贩经营点中随机抽取100个进行政策问询.如果按照分层抽样的方式随机抽取,请问应抽取小吃类、果蔬类商贩各多少家?
(2)为了更好地了解商户的收入情况,工作人员还对某果蔬经营点最近40天的日收入进行了统计(单位:元),所得频率分布直方图如图2.
(ⅰ)请根据频率分布直方图估计该果蔬经营点的日平均收入(同一组中的数据用该组区间的中点值为代表);
(ⅱ)若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
解:(1)由题意知,小吃类所占比例为:
1﹣25%﹣15%﹣10%﹣5%﹣5%=40%,
按照分层抽样的方式随机抽取,
应抽取小吃类商贩:100×40%=40(家),
果蔬类商贩100×15%=15(家).
(2)(i)该果蔬经营点的日平均收入为:
(75×0.002+125×0.009+175×0.006+225×0.002+275×0.001)×50=152.5(元).
(ⅱ)该果蔬经营点的日收入超过200元的天数为6,其中超过250元的有2天,
记日收入超过250元的2天为a1,a2,其余4天为b1,b2,b3,b4,
随机抽取两天的所有可能情况为:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),
(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b1),共15种,
其中至少有一天超过250元的所有可能情况为:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4),共9种.
所以这两天的日收入至少有一天超过250元的概率为P==.
21.(12分)已知椭圆的离心率为,抛物线C2的焦点与椭圆C1的右焦点F重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点.
(1)求的值;
(2)设M为C1与C2的公共点,若,求C1与C2的标准方程.
解:(1)因为椭圆C1的离心率为,所以设其方程为,F(c,0),
令x=c解得y=,所以AB=3c,
又抛物线C2的焦点与椭圆C1的右焦点F(c,0)重合,所以设其方程为y2=4cx,
令x=c解得y=±2c,所以CD=4c,
故;
(2)由,消去y得:3x2+16cx﹣12c2=0,解得x=或﹣6c(舍去),
所以M(),
因为OM=,所以,
所以c=1,
即椭圆方程为,抛物线方程为y2=4x.
22.(12分)如图,四边形ABCD与四边形BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(Ⅰ)求证:平面ACF⊥平面ABCD;
(Ⅱ)求二面角A﹣FC﹣B的余弦值.
【解答】(Ⅰ)证明:AC与BD交于点O,连接FO、FD,
∵FA=FC,O是AC中点,且O是BD中点,∴FO⊥AC,
∵四边形BDEF为菱形,∠DBF=60°,
∴FD=FB,∴FO⊥BD,
又AC∩BD=0,∴FO⊥平面ABCD,
∵FO⊥平面ACF,∴平面ACF⊥平面ABCD.
(Ⅱ)解:易知OA,OB,OF两两垂直,
以O为原点,OA、OB、OF分别为x、y、z轴建立如图所示的空间直角坐标系,
设AB=2,∵四边形ABCD为菱形,∠DAB=60°,
则BD=2,∴OB=1,,
故O(0,0,0),B(0,1,0),,,
∴,,,
设平面BFC的一个法向量为,
则,取x=1,得,
显然,为平面ACF的一个法向量,
∴,
由图知,二面角A﹣FC﹣B的平面角为锐角,
∴二面角A﹣FC﹣B得余弦值为.
一、选择题(共12小题).
1.(5分)已知集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},则A∩B=( )
A.{﹣1,0,1} B.{1,2} C.{0,1,2} D.{0,1}
2.(5分)已知等比数列{an}的各项都是正数,且a3a7=9,则a5=( )
A.9 B.﹣3 C.3 D.±3
3.(5分)若α∈R,sinα?cosα<0,tanα?sinα<0,则α是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
4.(5分)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A. B.
C. D.
5.(5分)如图,在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若=,=,=,则下列向量中与相等的向量是( )
A.﹣++ B. C.﹣﹣+ D.
6.(5分)已知x<﹣1,那么在下列不等式中,不成立的是( )
A.x2﹣1>0 B. C.sinx﹣x>0 D.cosx+x>0
7.(5分)已知直线l?平面α,则“直线m⊥平面α”是“m⊥l”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
8.(5分)已知过点M(2,﹣4)的直线l与圆C:(x﹣1)2+(y+2)2=5相切,且与直线m:ax﹣2y+3=0垂直,则实数a的值为( )
A.4 B.2 C.﹣2 D.﹣4
9.(5分)已知函数f(x)=ax2﹣x(a≠0),若对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,则实数a的取值范围是( )
A. B. C. D.
10.(5分)边长为4的正方形ABCD的四个顶点都在球O上,OA与平面ABCD所成角为,则球O的表面积为( )
A.64π B.32π C.16π D.128π
11.(5分)已知是一个等差数列的前n项和,对于函数f(x)=x2﹣ax,若数列的前n项和为Tn,则T2020的值为( )
A. B. C. D.
12.(5分)已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+∞) D.(2,+∞)
二、填空题(共4小题).
13.(5分)已知向量、不共线,,,若,则实数m= .
14.(5分)某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为 .
15.(5分)为了净化水质,向一游泳池加入某种药品,加药后,池水中该药品的浓度C(单位:mg/L)随时间t(单位:h)的变化关系为,则池水中药品的浓度最大可达到 mg/L.
16.(5分)已知函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)的图象,现有如下命题:
p1:函数g(x)的最小正周期是2π;
p2:函数g(x)在区间上单调递增;
p3:函数g(x)在区间上的值域为[﹣1,2].
则下述命题中所有真命题的序号是 .
①(¬p2)∧p3;②p1∨(¬p3);③p2∨p3;④p1∧p2.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(Ⅰ)解不等式;
(Ⅱ)已知函数f(x)=mx2﹣mx﹣1(m≠0),若f(x)<0对于一切实数x都成立,求m的取值范围.
18.(12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(1)求an;
(2)设,证明数列{bn}是等比数列,并求其前n项和Tn.
19.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2A+sin2C﹣sin2B=sinAsinC,c=2.
(1)求sinB的值;
(2)设D在BC边上,且BD=AD=2DC,求△ABC的面积.
20.(12分)为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,各类商贩所占比例如图1.
(1)该市城管委为了更好地服务百姓,打算从流动商贩经营点中随机抽取100个进行政策问询.如果按照分层抽样的方式随机抽取,请问应抽取小吃类、果蔬类商贩各多少家?
(2)为了更好地了解商户的收入情况,工作人员还对某果蔬经营点最近40天的日收入进行了统计(单位:元),所得频率分布直方图如图2.
(ⅰ)请根据频率分布直方图估计该果蔬经营点的日平均收入(同一组中的数据用该组区间的中点值为代表);
(ⅱ)若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
21.(12分)已知椭圆的离心率为,抛物线C2的焦点与椭圆C1的右焦点F重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点.
(1)求的值;
(2)设M为C1与C2的公共点,若,求C1与C2的标准方程.
22.(12分)如图,四边形ABCD与四边形BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(Ⅰ)求证:平面ACF⊥平面ABCD;
(Ⅱ)求二面角A﹣FC﹣B的余弦值.
参考答案
一、选择题(共12小题).
1.(5分)已知集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},则A∩B=( )
A.{﹣1,0,1} B.{1,2} C.{0,1,2} D.{0,1}
解:集合A={﹣2,﹣1,0,1,2},B={x|﹣1<x≤2},
则A∩B={0,1,2}.
故选:C.
2.(5分)已知等比数列{an}的各项都是正数,且a3a7=9,则a5=( )
A.9 B.﹣3 C.3 D.±3
解:等比数列{an}的各项都是正数,且a3a7=9,则a52=a3a7=9,
∴a5=3,
故选:C.
3.(5分)若α∈R,sinα?cosα<0,tanα?sinα<0,则α是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
解:∵sinα?cosα<0,
∴α在第二四象限,
∵tanα?sinα<0,
∴α在第二三象限,
故α的终边在第二象限,
故选:B.
4.(5分)如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )
A. B.
C. D.
解:由已知中的空间几何体的正视图和俯视图可得:
该几何体是一个底面半径为1,高为1的圆柱挖去一个同底等高的圆锥所得的组合体,
故其侧视图为:
故选:B.
5.(5分)如图,在平行六面体ABCD﹣A1B1C1D1中,M为A1C1与B1D1的交点.若=,=,=,则下列向量中与相等的向量是( )
A.﹣++ B. C.﹣﹣+ D.
解:=+=+=+(+)=+(+),
故选:B.
6.(5分)已知x<﹣1,那么在下列不等式中,不成立的是( )
A.x2﹣1>0 B. C.sinx﹣x>0 D.cosx+x>0
解:∵x<﹣1,∴x2﹣1>0,x+<﹣2,
又∵sinx,cosx∈[﹣1,1],
∴sinx﹣x>0,cosx+x<0.
可得:ABC成立,D不成立.
故选:D.
7.(5分)已知直线l?平面α,则“直线m⊥平面α”是“m⊥l”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解:若直线m垂直于平面α,则直线m必垂直平面内的直线l,
但直线m要垂直于平面α,则m要垂直于平面α内的两条相交直线,故m⊥l无法推知直线m⊥平面α,
故“直线m⊥平面α”是“m⊥l”的充分不必要条件,
故选:A.
8.(5分)已知过点M(2,﹣4)的直线l与圆C:(x﹣1)2+(y+2)2=5相切,且与直线m:ax﹣2y+3=0垂直,则实数a的值为( )
A.4 B.2 C.﹣2 D.﹣4
解:根据题意,圆C:(x﹣1)2+(y+2)2=5,圆心C(1,﹣2),
而点M(2,﹣4),则有(2﹣1)2+(﹣4+2)2=5,则点M在圆C上,
若过点M的切线与直线m:ax﹣2y+3=0垂直,则直线CM与直线m平行,
而直线MC的斜率k==﹣2,
则有=﹣2,则a=﹣4,
故选:D.
9.(5分)已知函数f(x)=ax2﹣x(a≠0),若对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,则实数a的取值范围是( )
A. B. C. D.
解:因为f(x)=ax2﹣x对任意x1,x2∈[2,+∞),且x1<x2,都有[f(x1)﹣f(x2)]?(x1﹣x2)>0,
所以f(x1)﹣f(x2)<0即f(x1)<f(x2),
所以f(x)在[2,+∞)上单调递增,
,解得,a.
故选:C.
10.(5分)边长为4的正方形ABCD的四个顶点都在球O上,OA与平面ABCD所成角为,则球O的表面积为( )
A.64π B.32π C.16π D.128π
解:如图,设正方形ABCD外接圆的圆心为O1,由题意,,则,表面积S=4π?42=64π.
故选:A.
11.(5分)已知是一个等差数列的前n项和,对于函数f(x)=x2﹣ax,若数列的前n项和为Tn,则T2020的值为( )
A. B. C. D.
解:是一个等差数列的前n项和,
可得a+1=0,解得a=﹣1,
所以函数f(x)=x2+x,
数列即,=,
所以数列的前n项和为Tn==1﹣,
则T2020=1﹣=.
故选:D.
12.(5分)已知双曲线的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+∞) D.(2,+∞)
解:已知双曲线的右焦点为F,
若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,
则该直线的斜率的绝对值小于等于渐近线的斜率,
∴≥,离心率e2=,
∴e≥2,
故选:C.
二、填空题(本大题共4小题,每小题5分,共20分)
13.(5分)已知向量、不共线,,,若,则实数m= ﹣3 .
解:向量、不共线,,,
若,则m﹣3(m+2)=0,
解得m=﹣3.
故答案为:﹣3.
14.(5分)某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,则不中奖的概率为 0.39 .
解:某商店的有奖促销活动中仅有一等奖、二等奖、鼓励奖三个奖项,
其中中一等奖的概率为0.05,中二等奖的概率为0.16,中鼓励奖的概率为0.40,
则不中奖的概率为P=1﹣0.05﹣0.16﹣0.40=0.39.
故答案为:0.39.
15.(5分)为了净化水质,向一游泳池加入某种药品,加药后,池水中该药品的浓度C(单位:mg/L)随时间t(单位:h)的变化关系为,则池水中药品的浓度最大可达到 4 mg/L.
解:∵t>0,
∴==4,当且仅当t=即t=3时,等号成立,
∴池水中药品的浓度最大可达到4mg/L.
故答案为:4.
16.(5分)已知函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)的图象,现有如下命题:
p1:函数g(x)的最小正周期是2π;
p2:函数g(x)在区间上单调递增;
p3:函数g(x)在区间上的值域为[﹣1,2].
则下述命题中所有真命题的序号是 ①③ .
①(¬p2)∧p3;②p1∨(¬p3);③p2∨p3;④p1∧p2.
解:函数,将函数f(x)的图象向右平移个单位长度后,得到函数g(x)=2sin(2x﹣)的图象,
所以:A:函数的最小正周期为π,故p1为假命题,
B:当时,故,所以函数的图象先减后增,故p2为假命题;¬p2为真命题;
C:当时,所以,则g(x)∈[﹣1,2],故p3为真命题;¬p3为假命题;
所以:①(¬p2)∧p3为真命题;②p1∨(¬p3)为假命题;③p2∨p3为真命题;④p1∧p2为假命题;
故答案为:①③.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)(Ⅰ)解不等式;
(Ⅱ)已知函数f(x)=mx2﹣mx﹣1(m≠0),若f(x)<0对于一切实数x都成立,求m的取值范围.
解:(Ⅰ)根据题意,不等式可转化成不等式(2x﹣5)(x﹣3)≥0,但x≠3,
解得x>3或,
故原不等式的解集为;
(Ⅱ)根据题意,由于m≠0,f(x)=mx2﹣mx﹣1<0对于一切实数x都成立,
则有,解之得﹣4<m<0,
故m的取值范围是(﹣4,0).
18.(12分)设等差数列{an}的前n项和为Sn,S7=14,a2+a12=10.
(1)求an;
(2)设,证明数列{bn}是等比数列,并求其前n项和Tn.
【解答】解(1)根据题意,{an}是等差数列,
若S7=14,a2+a12=10,则有S7=7a1+21d=14,a2+a12=2a1+12d=10,
联立解得a1=﹣1,d=1,
所以an=n﹣2;
(2)证明:由=2n﹣2,则,
故列{bn}是首项为,公比为2的等比数列.
数列{bn}的前n项和.
19.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,若sin2A+sin2C﹣sin2B=sinAsinC,c=2.
(1)求sinB的值;
(2)设D在BC边上,且BD=AD=2DC,求△ABC的面积.
解:(1)△ABC中,sin2A+sin2C﹣sin2B=sinAsinC,
由正弦定理得,a2+c2﹣b2=ac,
所以cosB===;
又B∈(0,π),
所以sinB===;
(2)如图所示,
设BD=AD=2DC=x,由c=AB=2,
利用余弦定理得,AD2=AB2+BD2﹣2AB?BD?cosB,
即x2=22+x2﹣2×2×x×,
解得x=3,CD=x=,
所以△ABC的面积为
S△ABC=AB?BC?sinB=×2×(3+)×=3.
20.(12分)为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,各类商贩所占比例如图1.
(1)该市城管委为了更好地服务百姓,打算从流动商贩经营点中随机抽取100个进行政策问询.如果按照分层抽样的方式随机抽取,请问应抽取小吃类、果蔬类商贩各多少家?
(2)为了更好地了解商户的收入情况,工作人员还对某果蔬经营点最近40天的日收入进行了统计(单位:元),所得频率分布直方图如图2.
(ⅰ)请根据频率分布直方图估计该果蔬经营点的日平均收入(同一组中的数据用该组区间的中点值为代表);
(ⅱ)若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
解:(1)由题意知,小吃类所占比例为:
1﹣25%﹣15%﹣10%﹣5%﹣5%=40%,
按照分层抽样的方式随机抽取,
应抽取小吃类商贩:100×40%=40(家),
果蔬类商贩100×15%=15(家).
(2)(i)该果蔬经营点的日平均收入为:
(75×0.002+125×0.009+175×0.006+225×0.002+275×0.001)×50=152.5(元).
(ⅱ)该果蔬经营点的日收入超过200元的天数为6,其中超过250元的有2天,
记日收入超过250元的2天为a1,a2,其余4天为b1,b2,b3,b4,
随机抽取两天的所有可能情况为:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),
(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b1),共15种,
其中至少有一天超过250元的所有可能情况为:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),(a2,b4),共9种.
所以这两天的日收入至少有一天超过250元的概率为P==.
21.(12分)已知椭圆的离心率为,抛物线C2的焦点与椭圆C1的右焦点F重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点.
(1)求的值;
(2)设M为C1与C2的公共点,若,求C1与C2的标准方程.
解:(1)因为椭圆C1的离心率为,所以设其方程为,F(c,0),
令x=c解得y=,所以AB=3c,
又抛物线C2的焦点与椭圆C1的右焦点F(c,0)重合,所以设其方程为y2=4cx,
令x=c解得y=±2c,所以CD=4c,
故;
(2)由,消去y得:3x2+16cx﹣12c2=0,解得x=或﹣6c(舍去),
所以M(),
因为OM=,所以,
所以c=1,
即椭圆方程为,抛物线方程为y2=4x.
22.(12分)如图,四边形ABCD与四边形BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
(Ⅰ)求证:平面ACF⊥平面ABCD;
(Ⅱ)求二面角A﹣FC﹣B的余弦值.
【解答】(Ⅰ)证明:AC与BD交于点O,连接FO、FD,
∵FA=FC,O是AC中点,且O是BD中点,∴FO⊥AC,
∵四边形BDEF为菱形,∠DBF=60°,
∴FD=FB,∴FO⊥BD,
又AC∩BD=0,∴FO⊥平面ABCD,
∵FO⊥平面ACF,∴平面ACF⊥平面ABCD.
(Ⅱ)解:易知OA,OB,OF两两垂直,
以O为原点,OA、OB、OF分别为x、y、z轴建立如图所示的空间直角坐标系,
设AB=2,∵四边形ABCD为菱形,∠DAB=60°,
则BD=2,∴OB=1,,
故O(0,0,0),B(0,1,0),,,
∴,,,
设平面BFC的一个法向量为,
则,取x=1,得,
显然,为平面ACF的一个法向量,
∴,
由图知,二面角A﹣FC﹣B的平面角为锐角,
∴二面角A﹣FC﹣B得余弦值为.
同课章节目录
