人教版数学八年级下册 20.1.1 平均数课时2 平均数的应用 课件(25张)
文档属性
| 名称 | 人教版数学八年级下册 20.1.1 平均数课时2 平均数的应用 课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 309.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 10:44:56 | ||
图片预览





文档简介
第二十章 数据的分析
20.1数据的集中趋势
20.1.1 平均数
课时2 平均数的应用
1.理解组中值的意义,能利用组中值计算一组数据的加权平均数;(重点、难点)
2.会用计算器求一组数据的加权平均数;
3.理解用样本的平均数估计总体的平均数的意义.
学习目标
新课导入
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的______.
权
复习引入
新课讲解
知识点1 组中值与平均数
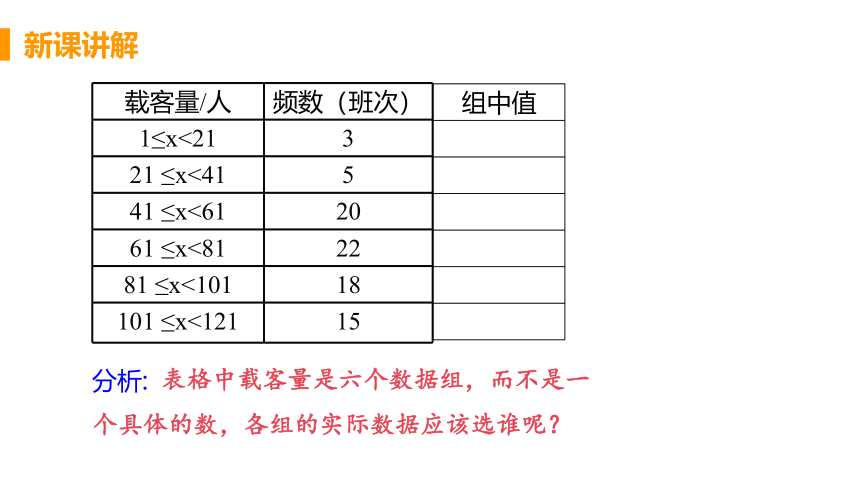
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人
频数(班次)
1≤x<21
3
21 ≤x<41
5
41 ≤x<61
20
61 ≤x<81
22
81 ≤x<101
18
101 ≤x<121
15
新课讲解
载客量/人
频数(班次)
1≤x<21
3
21 ≤x<41
5
41 ≤x<61
20
61 ≤x<81
22
81 ≤x<101
18
101 ≤x<121
15
表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
组中值
分析:
新课讲解
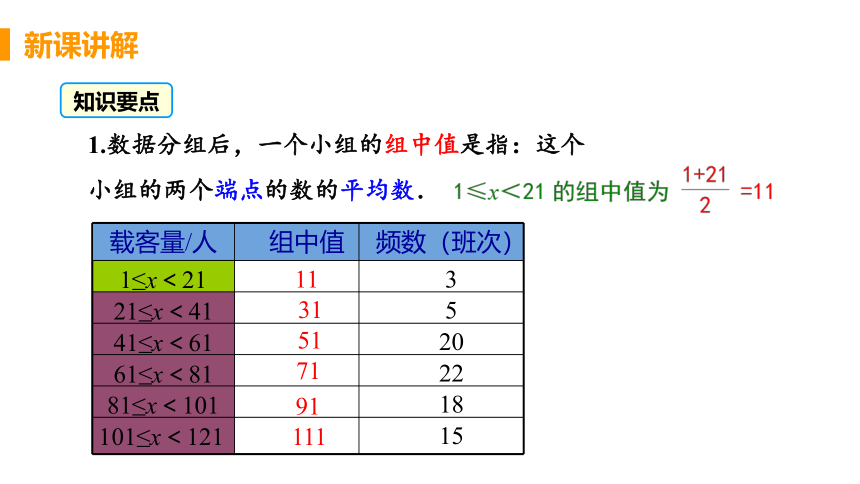
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
知识要点
新课讲解
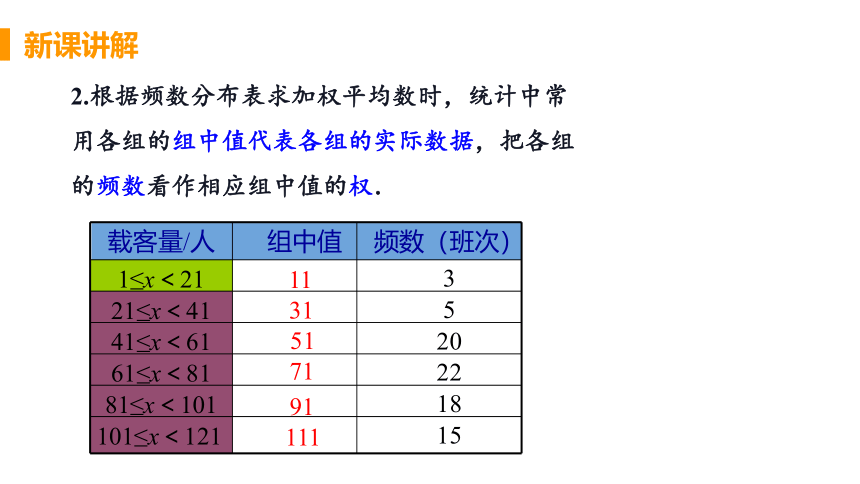
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
新课讲解
解:这天5路公共汽车平均每班的载客量是
新课讲解
知识点2 用样本平均数估计总体平均数
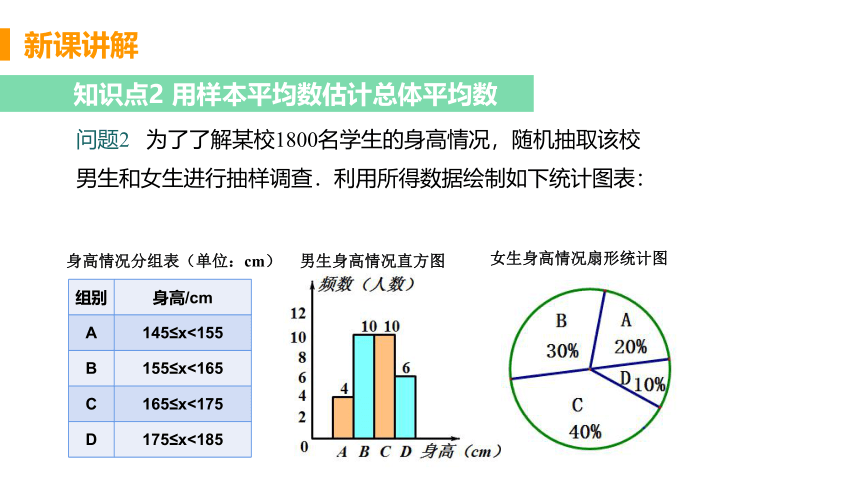
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
新课讲解
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
新课讲解
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
新课讲解
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
用样本的平均数可以估计总体的平均数.
新课讲解
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
新课讲解
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
新课讲解
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
做一做
10
15
20
18
新课讲解
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
解:
课堂小结
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
用计算器求平均数
用样本平均数估计总体平均数
当堂小练
年 龄
频数
28≤X<30
4
30≤X<32
4
32≤X<34
8
34≤X<36
8
36≤X<38
12
38≤X<40
14
40≤X<42
6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
当堂小练
2.某班40名学生身高情况如下图,请计算该班
学生平均身高.
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数
0
150
160
170
180
当堂小练
解:
答:该班学生平均身高为165.5cm.
当堂小练
3.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
=
= 22.351
即样本平均数为 22.351 答:这批零件的平均长度大约是22.351mm.
4.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
拓展与延伸
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
拓展与延伸
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
拓展与延伸
布置作业
请完成对应习题
20.1数据的集中趋势
20.1.1 平均数
课时2 平均数的应用
1.理解组中值的意义,能利用组中值计算一组数据的加权平均数;(重点、难点)
2.会用计算器求一组数据的加权平均数;
3.理解用样本的平均数估计总体的平均数的意义.
学习目标
新课导入
1.若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,
则__________________叫做这n个数的加权平均数.
2.在求一组数据的平均数时,某个数据出现的次数看作是这个数的______.
权
复习引入
新课讲解
知识点1 组中值与平均数
问题1: 为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人
频数(班次)
1≤x<21
3
21 ≤x<41
5
41 ≤x<61
20
61 ≤x<81
22
81 ≤x<101
18
101 ≤x<121
15
新课讲解
载客量/人
频数(班次)
1≤x<21
3
21 ≤x<41
5
41 ≤x<61
20
61 ≤x<81
22
81 ≤x<101
18
101 ≤x<121
15
表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
组中值
分析:
新课讲解
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
知识要点
新课讲解
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
新课讲解
解:这天5路公共汽车平均每班的载客量是
新课讲解
知识点2 用样本平均数估计总体平均数
问题2 为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
新课讲解
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况扇形统计图
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
新课讲解
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
新课讲解
(3)若抽样的女生为m人,女生的平均身高会改变吗?若改变,请计算;若不变,请说明理由.
(4)根据以上结果,你能估计该校女生的平均身高吗?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}组别
身高/cm
A
145≤x<155
B
155≤x<165
C
165≤x<175
D
175≤x<185
男生身高情况直方图
女生身高情况扇形统计图
用样本的平均数可以估计总体的平均数.
新课讲解
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
抽出50只灯泡的使用寿命组成一个样本,可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.
新课讲解
解:据上表得各小组的组中值,于是
即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是
1 672 h.
新课讲解
株数
黄瓜根数
0
5
10
15
20
10
13
14
15
种菜能手李大叔种植了一批新品种的黄瓜,为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形图,请估计这个新品种黄瓜平均每株结多少根黄瓜.
做一做
10
15
20
18
新课讲解
答:估计这个新品种黄瓜平均每株约结13根黄瓜.
解:
课堂小结
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
用计算器求平均数
用样本平均数估计总体平均数
当堂小练
年 龄
频数
28≤X<30
4
30≤X<32
4
32≤X<34
8
34≤X<36
8
36≤X<38
12
38≤X<40
14
40≤X<42
6
1.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
当堂小练
2.某班40名学生身高情况如下图,请计算该班
学生平均身高.
165
10
5
身高(cm)
185
175
155
145
15
20
6
10
20
4
人数
0
150
160
170
180
当堂小练
解:
答:该班学生平均身高为165.5cm.
当堂小练
3.为了检查一批零件的质量,从中随机抽取10件,
测得它们的长度(单位:mm)如下:
22.36 22.35 22.33 22.35 22.37
22.34 22.38 22.36 22.32 22.35
根据以上数据,估计这批零件的平均长度.
解:根据以上数据,得
=
= 22.351
即样本平均数为 22.351 答:这批零件的平均长度大约是22.351mm.
4.下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
拓展与延伸
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%
=60(分)
拓展与延伸
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
拓展与延伸
布置作业
请完成对应习题
