北师大版九年级下册 第3章 《圆》高频考点专题练习一遍过(二)(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册 第3章 《圆》高频考点专题练习一遍过(二)(Word版 含解析) | 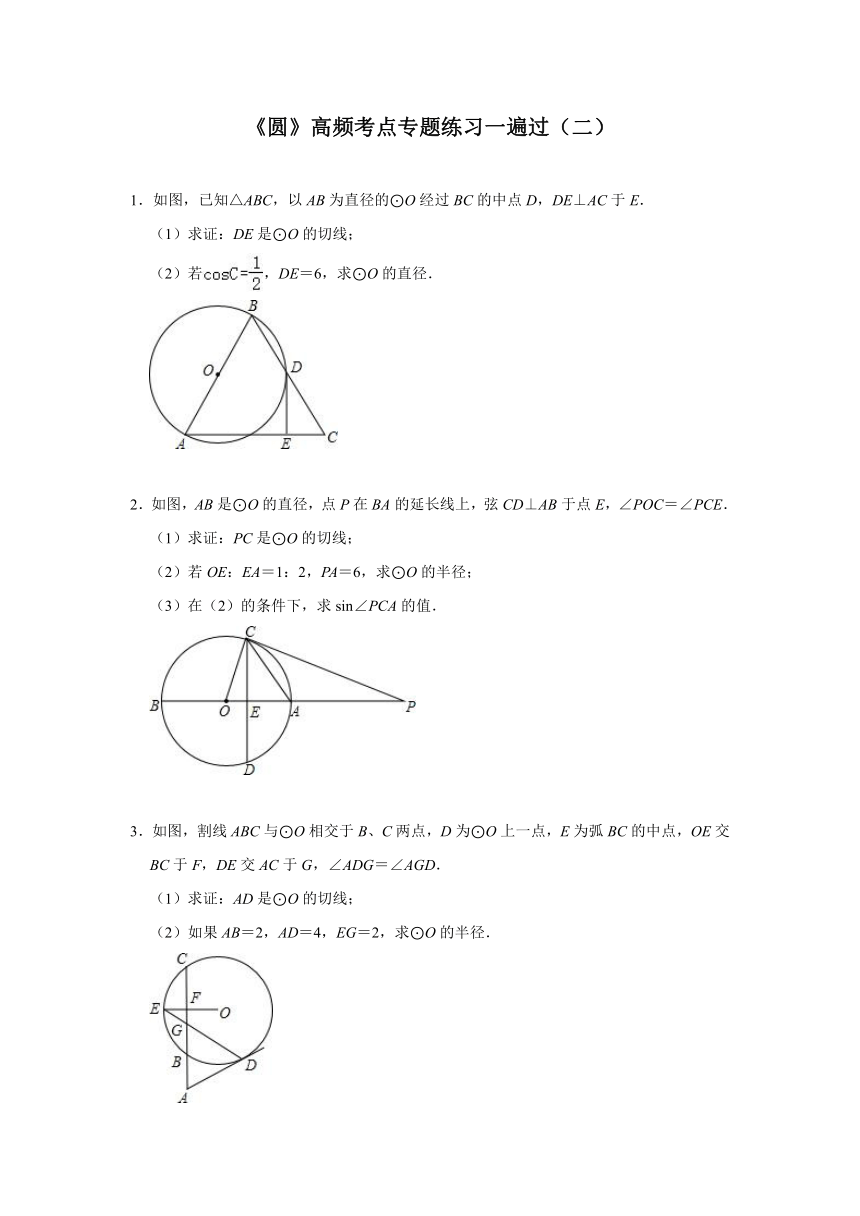 | |
| 格式 | zip | ||
| 文件大小 | 155.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 10:22:20 | ||
图片预览





文档简介
《圆》高频考点专题练习一遍过(二)
1.如图,已知△ABC,以AB为直径的⊙O经过BC的中点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若,DE=6,求⊙O的直径.
2.如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于点E,∠POC=∠PCE.
(1)求证:PC是⊙O的切线;
(2)若OE:EA=1:2,PA=6,求⊙O的半径;
(3)在(2)的条件下,求sin∠PCA的值.
3.如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
(1)求证:AD是⊙O的切线;
(2)如果AB=2,AD=4,EG=2,求⊙O的半径.
4.在△ABC中,∠ACB=90°,以AC为直径的圆交斜边AB于点P.E是BC的中点,连接PE.
(1)如果圆O的半径为2,∠B=30°,求OE的长;
(2)求证:PE是⊙O的切线.
5.如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长是关于x的方程的两根,求线段EB的长.
6.如图,在Rt△ABC中,已知∠C=90°,以AB为直径作⊙O,P是AB上一点,过点P作AB的垂线交AC的延长线于点Q,D是PQ上一点,DC=DQ.
(1)求证:DC是⊙O的切线;
(2)若∠A=60°,BC=QC,求的值.
7.如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=∠AOB.
(1)求证:MN是⊙O的切线;
(2)延长CB交MN于点D,求AD的长.
8.已知:如图,⊙O为△ABC的外接圆,BC为⊙O的直径,作射线BF,使得BA平分∠CBF,过点A作AD⊥BF于点D.
(1)求证:DA为⊙O的切线;
(2)若BD=1,,求⊙O的半径.
9.如图,AB是⊙O的直径,AE平分∠BAF交⊙O于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(1)求证:CD是⊙O的切线;
(2)若∠C=30°,DE=,求⊙O的直径.
10.如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,BF⊥AB交AD的延长线于点F,
(1)求证:DE是⊙O的切线;
(2)若DE=3,⊙O的半径为5,求BF的长.
参考答案
1.(1)证明:如图,连接OD;(1分)
∵DE⊥AC,
∴∠DEC=90°.
∵O为AB中点,D为BC中点,
∴OD为△ABC的中位线.
∴OD∥AC.
∴∠ODE=∠DEC=90°.
即OD⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线.解:∵,
∴∠C=60°.(3分)
∵OD∥AC,
∴∠BDO=∠C=60°.
∵OD=OB,
∴∠B=∠ODB=60°.
∴△ABC为等边三角形.
∵在△EDC中,∠DEC=90°,DE=6,
∴.(4分)
∵D为BC中点,
∴.
∴AB=.
∴⊙O的直径为.(5分)
2.(1)证明:∵弦CD⊥AB于点E,
∴∠CEP=90°.
∵∠POC=∠PCE,∠P=∠P,
∴△POC∽△PCE,
∴∠PCO=∠CEP=90°.
∴PC是⊙O的切线.
(2)解:∵OE:EA=1:2,
∴OE:OC=,
∴OC:OP=.
∵PA=6,
∴⊙O的半径=3.
(3)解:连接BC;
∵圆的半径为3,OE:EA=1:2,
∴OE=1,
∴EC=2,BE=4;
∴BC=2.
∵∠PCA=∠B,
∴sin∠B=sin∠PCA==.
3.(1)证明:连接OD.
∵E为BC的中点,
∴OE⊥BC于F.
∴∠AGD+∠ODE=∠EGF+∠OED=90°.
则OD=OE,
∴∠ODE=∠OED.
∵∠AGD=∠ADG,
∴∠ADG+∠ODE=90°.
即OD⊥AD,
∴AD是⊙O的切线.
(2)解:∵AD=4,AB=2,AD2=ABAC;
∴AC=8.
∵AD=AG,
∴BG=2,CG=4.
∵EG=2,EGGD=BGCG,
∴DG=4,
∴AD=DG=AG.
∴∠ADG=60°.
作OH⊥ED于H,则∠EOH=60°,
在Rt△OEH中,EH=(EG+GD)=3.
∴OE==.
即⊙O的半径为.
4.解:(1)∵圆O的半径为2,
∴AC=4.
∵∠ACB=90°,∠B=30°,
∴AB=8.
∵E是BC的中点,OA=OC,
∴OE=4;
证明:(2)连接OP.
∵E是BC的中点,OA=OC,
∴OE∥AB,
∴∠AP0=∠POE,∠A=∠EOC,
∵OA=OP,
∴∠A=∠APO,
∴∠POE=∠COE,
∵OP=OC,OE=OE,
∴△POE≌△COE.
∴∠OPE=∠ACB=90°.
∴PE是⊙O的切线.
5.(1)证明:连接OD.
∵AO为半圆直径,∴∠ADO=90°.
∴AE切⊙O于点D;
(2)∵AC、AD的长是关于x的方程的两根,
∴ACAD=4;
∵AC=2,
∴AD=2.
设OD=OC=x,则(x+2)2=(2)2+x2.
解得x=4.
∴AB=2+8=10.
∵∠ADO=∠ABE=90°,∠A=∠A,
∴△AOD∽△AEB,
∴,即,
∴BE=4.
6.(1)证明:连接OC;
∵OA=OC,
∴∠OCA=∠A,
∵CD=DQ,
∴∠DCQ=∠Q,
∴∠OCA+∠DCQ=∠A+∠Q=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)解:设⊙O的半径为r,则AB=2r,OC=r,AC=0.5AB=r,BC=r;
∴CQ=BC=r,AQ=AC+CQ=(1+)r,
PQ=AQc0s60°=0.5(1+)r;
∴BP=AB﹣AP=0.5(3﹣)r,PO=AP﹣OA=0.5(﹣1)r,
∴BP:PO=.
7.(1)证明:∵AC是直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM=∠AOB=∠C,
∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)解:∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC==,
∴,
∴AD=.
8.(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵BD=1,,
∴AD=2,
∴AB==,
∴cos∠DBA=;
∵∠DBA=∠CBA,
∴BC===5.
∴⊙O的半径为2.5.
9.(1)证明:连接OE,则∠OAE=∠OEA.
由∠OAE=∠EAD得∠OEA=∠EAD,
所以OE∥AD.
因为AD⊥CD,所以OE⊥CD,
所以CD是⊙O的切线.
(2)解:过点O作OG⊥AD于点G.
则∠AOG=∠ACD=30°,四边形OEDG为矩形.
∴OG=ED=,
∴OA=2,
∴⊙O的直径是4.
10.(1)证明:连OD,如图,
∵AD平分∠BAC,
∴∠1=∠2(等弦对等角),
又∵OD=OA,得∠2=∠3(等角对等边),
∴∠1=∠3(等量代换),
而DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)过D作DP⊥AB,P为垂足,
∵AD为∠BAC的平分线,DE=3,
∴DP=DE=3,又⊙O的半径为5,
在Rt△OPD中,OD=5,DP=3,得OP=4,则AP=9,
∵BF⊥AB,
∴DP∥FB,
∴=,即=,
∴BF=.
1.如图,已知△ABC,以AB为直径的⊙O经过BC的中点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若,DE=6,求⊙O的直径.
2.如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB于点E,∠POC=∠PCE.
(1)求证:PC是⊙O的切线;
(2)若OE:EA=1:2,PA=6,求⊙O的半径;
(3)在(2)的条件下,求sin∠PCA的值.
3.如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
(1)求证:AD是⊙O的切线;
(2)如果AB=2,AD=4,EG=2,求⊙O的半径.
4.在△ABC中,∠ACB=90°,以AC为直径的圆交斜边AB于点P.E是BC的中点,连接PE.
(1)如果圆O的半径为2,∠B=30°,求OE的长;
(2)求证:PE是⊙O的切线.
5.如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长是关于x的方程的两根,求线段EB的长.
6.如图,在Rt△ABC中,已知∠C=90°,以AB为直径作⊙O,P是AB上一点,过点P作AB的垂线交AC的延长线于点Q,D是PQ上一点,DC=DQ.
(1)求证:DC是⊙O的切线;
(2)若∠A=60°,BC=QC,求的值.
7.如图,⊙O的直径AC=13,弦BC=12.过点A作直线MN,使∠BAM=∠AOB.
(1)求证:MN是⊙O的切线;
(2)延长CB交MN于点D,求AD的长.
8.已知:如图,⊙O为△ABC的外接圆,BC为⊙O的直径,作射线BF,使得BA平分∠CBF,过点A作AD⊥BF于点D.
(1)求证:DA为⊙O的切线;
(2)若BD=1,,求⊙O的半径.
9.如图,AB是⊙O的直径,AE平分∠BAF交⊙O于E,过E点作直线与AF垂直,交AF延长线于D点,且交AB的延长线于C点.
(1)求证:CD是⊙O的切线;
(2)若∠C=30°,DE=,求⊙O的直径.
10.如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,BF⊥AB交AD的延长线于点F,
(1)求证:DE是⊙O的切线;
(2)若DE=3,⊙O的半径为5,求BF的长.
参考答案
1.(1)证明:如图,连接OD;(1分)
∵DE⊥AC,
∴∠DEC=90°.
∵O为AB中点,D为BC中点,
∴OD为△ABC的中位线.
∴OD∥AC.
∴∠ODE=∠DEC=90°.
即OD⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线.解:∵,
∴∠C=60°.(3分)
∵OD∥AC,
∴∠BDO=∠C=60°.
∵OD=OB,
∴∠B=∠ODB=60°.
∴△ABC为等边三角形.
∵在△EDC中,∠DEC=90°,DE=6,
∴.(4分)
∵D为BC中点,
∴.
∴AB=.
∴⊙O的直径为.(5分)
2.(1)证明:∵弦CD⊥AB于点E,
∴∠CEP=90°.
∵∠POC=∠PCE,∠P=∠P,
∴△POC∽△PCE,
∴∠PCO=∠CEP=90°.
∴PC是⊙O的切线.
(2)解:∵OE:EA=1:2,
∴OE:OC=,
∴OC:OP=.
∵PA=6,
∴⊙O的半径=3.
(3)解:连接BC;
∵圆的半径为3,OE:EA=1:2,
∴OE=1,
∴EC=2,BE=4;
∴BC=2.
∵∠PCA=∠B,
∴sin∠B=sin∠PCA==.
3.(1)证明:连接OD.
∵E为BC的中点,
∴OE⊥BC于F.
∴∠AGD+∠ODE=∠EGF+∠OED=90°.
则OD=OE,
∴∠ODE=∠OED.
∵∠AGD=∠ADG,
∴∠ADG+∠ODE=90°.
即OD⊥AD,
∴AD是⊙O的切线.
(2)解:∵AD=4,AB=2,AD2=ABAC;
∴AC=8.
∵AD=AG,
∴BG=2,CG=4.
∵EG=2,EGGD=BGCG,
∴DG=4,
∴AD=DG=AG.
∴∠ADG=60°.
作OH⊥ED于H,则∠EOH=60°,
在Rt△OEH中,EH=(EG+GD)=3.
∴OE==.
即⊙O的半径为.
4.解:(1)∵圆O的半径为2,
∴AC=4.
∵∠ACB=90°,∠B=30°,
∴AB=8.
∵E是BC的中点,OA=OC,
∴OE=4;
证明:(2)连接OP.
∵E是BC的中点,OA=OC,
∴OE∥AB,
∴∠AP0=∠POE,∠A=∠EOC,
∵OA=OP,
∴∠A=∠APO,
∴∠POE=∠COE,
∵OP=OC,OE=OE,
∴△POE≌△COE.
∴∠OPE=∠ACB=90°.
∴PE是⊙O的切线.
5.(1)证明:连接OD.
∵AO为半圆直径,∴∠ADO=90°.
∴AE切⊙O于点D;
(2)∵AC、AD的长是关于x的方程的两根,
∴ACAD=4;
∵AC=2,
∴AD=2.
设OD=OC=x,则(x+2)2=(2)2+x2.
解得x=4.
∴AB=2+8=10.
∵∠ADO=∠ABE=90°,∠A=∠A,
∴△AOD∽△AEB,
∴,即,
∴BE=4.
6.(1)证明:连接OC;
∵OA=OC,
∴∠OCA=∠A,
∵CD=DQ,
∴∠DCQ=∠Q,
∴∠OCA+∠DCQ=∠A+∠Q=90°,
∴∠OCD=90°,
∴CD是⊙O的切线;
(2)解:设⊙O的半径为r,则AB=2r,OC=r,AC=0.5AB=r,BC=r;
∴CQ=BC=r,AQ=AC+CQ=(1+)r,
PQ=AQc0s60°=0.5(1+)r;
∴BP=AB﹣AP=0.5(3﹣)r,PO=AP﹣OA=0.5(﹣1)r,
∴BP:PO=.
7.(1)证明:∵AC是直径,
∴∠ABC=90°,∠C+∠BAC=90°.
∵∠BAM=∠AOB=∠C,
∴∠BAM+∠BAC=90°,即∠CAM=90°.
∴MN是⊙O的切线.
(2)解:∵∠ABC=90°,AC=13,BC=12,
∴AB=5.
∵tanC==,
∴,
∴AD=.
8.(1)证明:连接OA;
∵BC为⊙O的直径,BA平分∠CBF,AD⊥BF,
∴∠ADB=∠BAC=90°,∠DBA=∠CBA;
∵∠OAC=∠OCA,
∴∠DAO=∠DAB+∠BAO=∠BAO+∠OAC=90°,
∴DA为⊙O的切线.
(2)解:∵BD=1,,
∴AD=2,
∴AB==,
∴cos∠DBA=;
∵∠DBA=∠CBA,
∴BC===5.
∴⊙O的半径为2.5.
9.(1)证明:连接OE,则∠OAE=∠OEA.
由∠OAE=∠EAD得∠OEA=∠EAD,
所以OE∥AD.
因为AD⊥CD,所以OE⊥CD,
所以CD是⊙O的切线.
(2)解:过点O作OG⊥AD于点G.
则∠AOG=∠ACD=30°,四边形OEDG为矩形.
∴OG=ED=,
∴OA=2,
∴⊙O的直径是4.
10.(1)证明:连OD,如图,
∵AD平分∠BAC,
∴∠1=∠2(等弦对等角),
又∵OD=OA,得∠2=∠3(等角对等边),
∴∠1=∠3(等量代换),
而DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)过D作DP⊥AB,P为垂足,
∵AD为∠BAC的平分线,DE=3,
∴DP=DE=3,又⊙O的半径为5,
在Rt△OPD中,OD=5,DP=3,得OP=4,则AP=9,
∵BF⊥AB,
∴DP∥FB,
∴=,即=,
∴BF=.
