人教版七年级数学下册:5.2.2.1平行线的判定方法 同步训练(word版,含答案)
文档属性
| 名称 | 人教版七年级数学下册:5.2.2.1平行线的判定方法 同步训练(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 85.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 00:00:00 | ||
图片预览

文档简介
5.2.2.1平行线的判定方法
一、选择题
1.
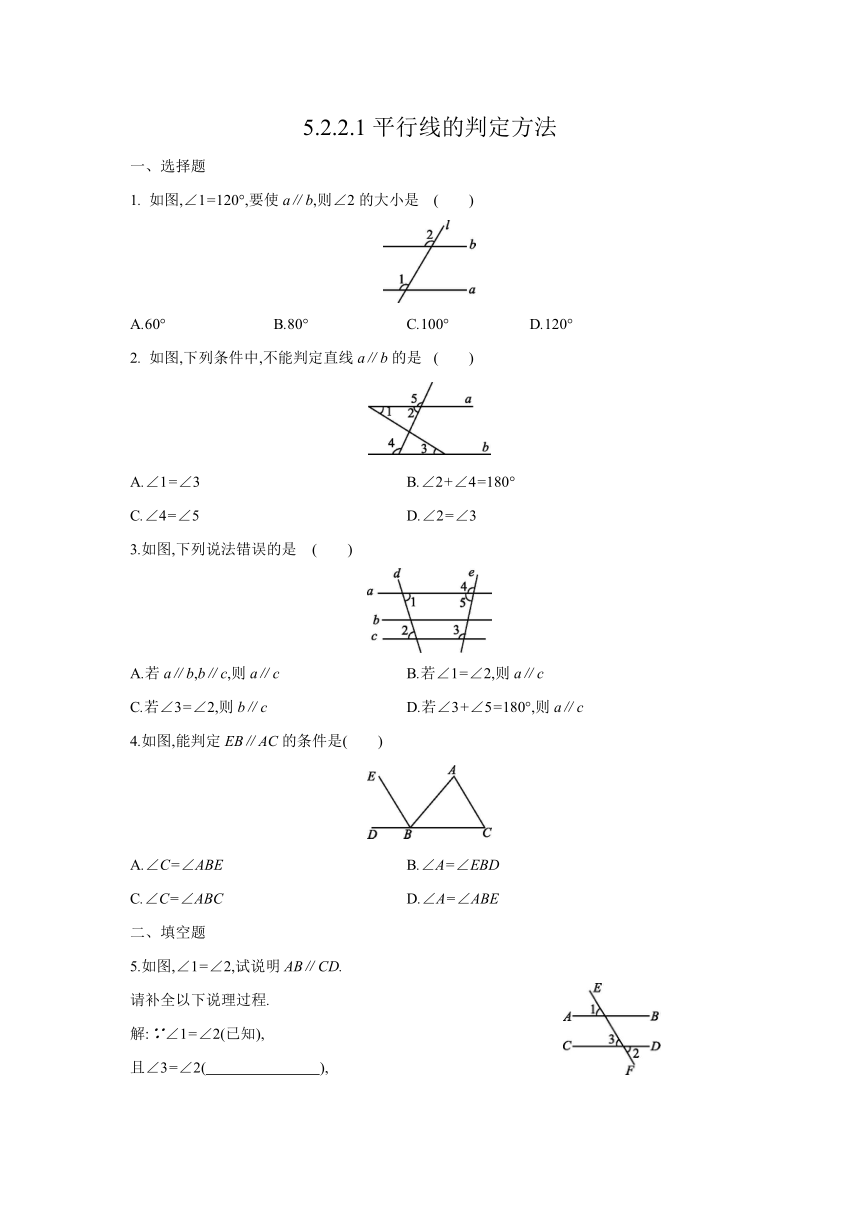
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
2.
如图,下列条件中,不能判定直线a∥b的是
( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠2=∠3
3.如图,下列说法错误的是
( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,能判定EB∥AC的条件是
( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE
二、填空题
5.如图,∠1=∠2,试说明AB∥CD.
请补全以下说理过程.
解:∵∠1=∠2(已知),
且∠3=∠2(
),?
∴∠1= ( ),?
∴AB∥CD(
).?
三、解答题
6.如图,∠1=60°,∠2=60°,∠3=120°.试说明:
(1)DE∥BC;
(2)DF∥AB.
7.如图,AB∥EF,∠1=60°,∠2=120°,则CD和EF平行吗?为什么?
8.
(1)如图所示,当∠BED与∠B,∠D满足 条件时,可以判定AB∥CD;?
(2)试说明你填写的条件的正确性.
参考答案
1.D 2.D 3.C 4.D
5.对顶角相等 ∠3 等量代换 同位角相等,两直线平行
6.解:(1)∵∠1=60°,∠2=60°,
∴∠1=∠2,
∴DE∥BC(同位角相等,两直线平行).
(2)如图,∵∠1=60°,
∴∠4=∠1=60°.
∵∠3=120°,
∴∠3+∠4=180°,
∴DF∥AB(同旁内角互补,两直线平行).
7.解:CD∥EF.
理由:∵∠1=60°,∠2=120°(已知),
∴∠1+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行).
∵AB∥EF(已知),
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
8.解:(1)∠BED=∠B+∠D
(2)如图,过点E在∠BED的内部作一个角∠BEF,使得∠BEF=∠B,
∴AB∥EF.
∵∠BED=∠B+∠D,
∴∠FED=∠D,
∴EF∥CD,
∴AB∥CD.
一、选择题
1.
如图,∠1=120°,要使a∥b,则∠2的大小是
( )
A.60°
B.80°
C.100°
D.120°
2.
如图,下列条件中,不能判定直线a∥b的是
( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠4=∠5
D.∠2=∠3
3.如图,下列说法错误的是
( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,能判定EB∥AC的条件是
( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE
二、填空题
5.如图,∠1=∠2,试说明AB∥CD.
请补全以下说理过程.
解:∵∠1=∠2(已知),
且∠3=∠2(
),?
∴∠1= ( ),?
∴AB∥CD(
).?
三、解答题
6.如图,∠1=60°,∠2=60°,∠3=120°.试说明:
(1)DE∥BC;
(2)DF∥AB.
7.如图,AB∥EF,∠1=60°,∠2=120°,则CD和EF平行吗?为什么?
8.
(1)如图所示,当∠BED与∠B,∠D满足 条件时,可以判定AB∥CD;?
(2)试说明你填写的条件的正确性.
参考答案
1.D 2.D 3.C 4.D
5.对顶角相等 ∠3 等量代换 同位角相等,两直线平行
6.解:(1)∵∠1=60°,∠2=60°,
∴∠1=∠2,
∴DE∥BC(同位角相等,两直线平行).
(2)如图,∵∠1=60°,
∴∠4=∠1=60°.
∵∠3=120°,
∴∠3+∠4=180°,
∴DF∥AB(同旁内角互补,两直线平行).
7.解:CD∥EF.
理由:∵∠1=60°,∠2=120°(已知),
∴∠1+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行).
∵AB∥EF(已知),
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
8.解:(1)∠BED=∠B+∠D
(2)如图,过点E在∠BED的内部作一个角∠BEF,使得∠BEF=∠B,
∴AB∥EF.
∵∠BED=∠B+∠D,
∴∠FED=∠D,
∴EF∥CD,
∴AB∥CD.
