人教版数学九年级下册 第27章 相似单元测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级下册 第27章 相似单元测试试题(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-24 10:27:11 | ||
图片预览



文档简介
相似单元测试试题(一)
一.选择题
1.在一幅地图上,用4cm表示哈尔滨工业大学到哈西客运站的地铁实际距离是8km,那么这幅地图的比例尺为( )
A.1:2
B.1:200
C.1:2000
D.1:200000
2.如图,在△ABC中,DE∥AB,且,则的值为( )
A.
B.
C.
D.
3.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm
B.32cm
C.48cm
D.52cm
4.若=,则的值为( )
A.
B.
C.
D.
5.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( )
A.AB2=BD?BC
B.AC2=DC?BC
C.AD2=BD?DC
D.BC2=AB?AC
6.如图,在平面直角坐标系中,已知△ABC与△DEF是位似图形,原点O是位似中心,位似比OA:OD=1:3,若AB=3,则DE的长为( )
A.5
B.6
C.9
D.12
7.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),C(0,6).已知矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,且矩形OA1B1C1的面积等于矩形OABC面积的,则点B1的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(4,3)
D.(4,3)或(﹣4,﹣3)
8.下列各组线段中不能构成比例线段的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=,c=,d=
C.a=0.1,b=0.2,c=1,d=0.5
D.a=4,b=6,c=5,d=10
9.如图,在△ABC中,点D在BC上一点,下列条件中,能使△ABC与△DAC相似的是( )
A.∠BAD=∠C
B.∠BAC=∠BDA
C.AB2=BD?BC
D.AC2=CD?CB
10.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F
B.G
C.H
D.K
二.填空题
11.点C在线段AB上,AB=1cm,若AC2=ABBC,那么线段AC的长为
cm.,点B(8,0),点C在线段AB上,AC=2,若以原点O为位似中心,把线段AB缩小为原来的,得到线段A′B′,则点C的对应点C′坐标为
.
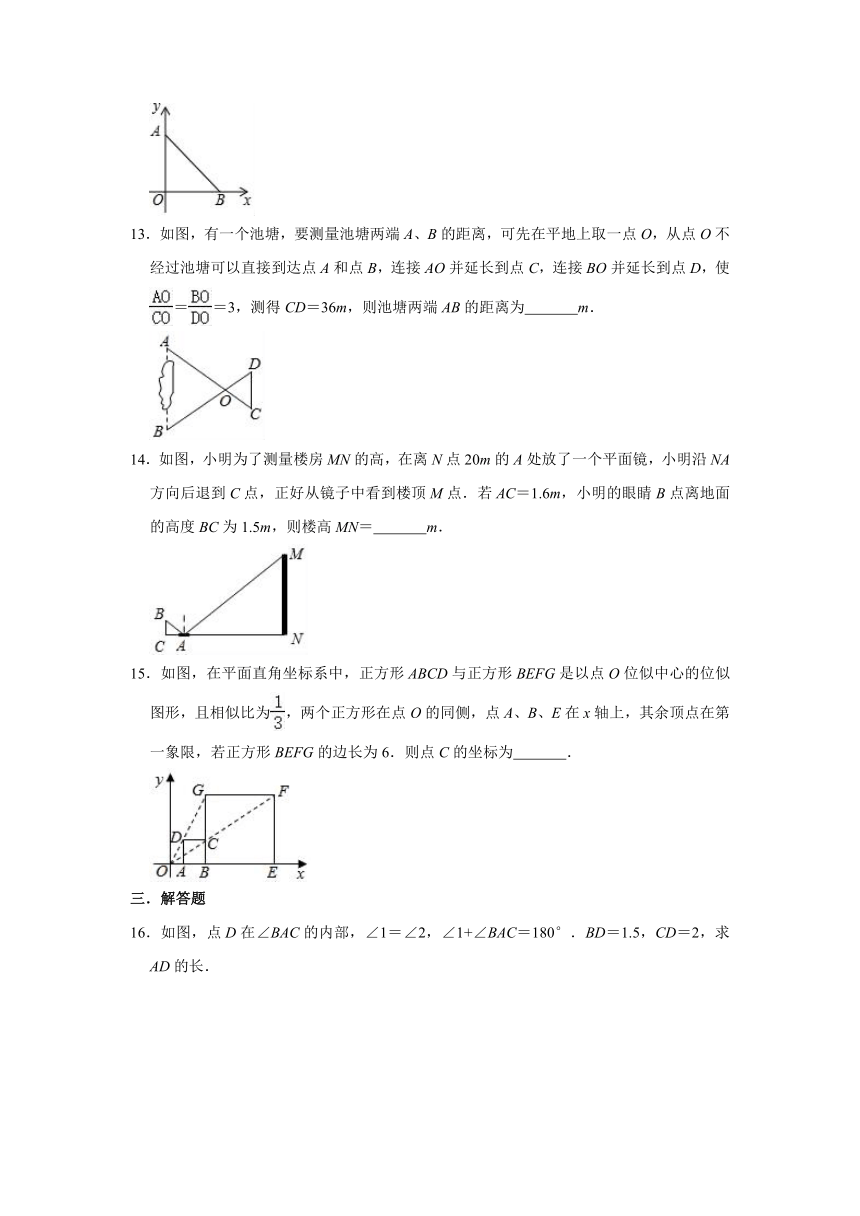
13.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为
m.
14.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=
m.
15.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以点O位似中心的位似图形,且相似比为,两个正方形在点O的同侧,点A、B、E在x轴上,其余顶点在第一象限,若正方形BEFG的边长为6.则点C的坐标为
.
三.解答题
16.如图,点D在∠BAC的内部,∠1=∠2,∠1+∠BAC=180°.BD=1.5,CD=2,求AD的长.
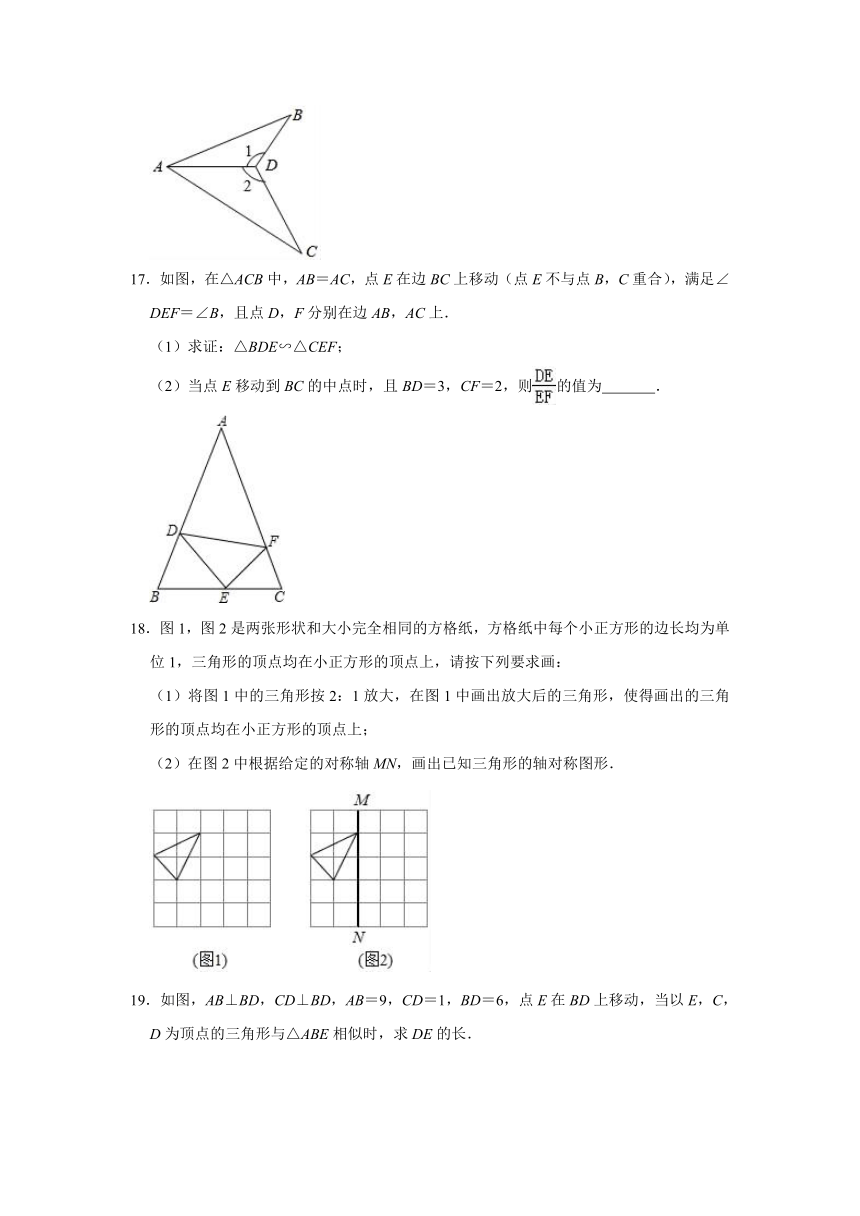
17.如图,在△ACB中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,且BD=3,CF=2,则的值为
.
18.图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为单位1,三角形的顶点均在小正方形的顶点上,请按下列要求画:
(1)将图1中的三角形按2:1放大,在图1中画出放大后的三角形,使得画出的三角形的顶点均在小正方形的顶点上;
(2)在图2中根据给定的对称轴MN,画出已知三角形的轴对称图形.
19.如图,AB⊥BD,CD⊥BD,AB=9,CD=1,BD=6,点E在BD上移动,当以E,C,D为顶点的三角形与△ABE相似时,求DE的长.
参考答案与试题解析
一.选择题
1.【解答】解:8km=800000cm,
4:800000=1:200000.
所以这幅地图的比例尺为1:200000.
故选:D.
2.【解答】解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
3.【解答】解:设较大多边形与较小多边形的周长分别是m,n.则==.
因而n=m.
根据面积之和是80cm2.得到m+m=80.
解得:m=48cm.
故选:C.
4.【解答】解:设==t,则a=3t,b=2t,
所以==.
故选:C.
5.【解答】解:如图,∠ABD=∠CBA,∠ADB=∠CAB=90°,
由射影定理知,AB2=BDBC,AC2=DCBC,AD2=BDDC,故选项A、B、C不符合题意.
ACAB=BCAD,即BCAD=ABAC.只有当AD=BC时BC2=ABAC才能成立,故选项D符合题意.故
故选:D.
6.【解答】解:∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴=,即=,
解得,DE=9,
故选:C.
7.【解答】解:∵矩形OA1B1C1O与矩形OABC位似,矩形OA1B1C1的面积等于矩形OABC面积的,
∴矩形OA1B1C1O与矩形OABC的位似比为1:,
∵矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,点B的坐标为(8,6),
∴点B1的坐标为为(8×,6×)或(﹣8×,﹣6×),即(4,3)或(4,3),
故选:D.
8.【解答】解:A、6×2=3×4,能构成比例线段;
B、1×=×,能构成比例线段;
C、0.1×1=0.2×0.5,能构成比例线段;
D、4×10≠5×6,不能构成比例线段.
故选:D.
9.【解答】解:选项A、B、C的条件无法判断△ABC与△DAC相似.
正确答案是D.理由如下:
∵AC2=CDCB,
∴,
∵∠C=∠C,
∴△ABC∽△DAC(两边成比例夹角相等的两个三角形相似).
故选:D.
10.【解答】解:根据题意,
△DEM∽△ABC,AB=4,AC=6
DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵AC2=ABBC,
∴点C是线段AB的黄金分割点,AC>BC,
∴AC=AB=×1=(cm),
故答案为:.
12.【解答】解:∵点A(0,8),点B(8,0),点C在线段AB上,AC=2,
∴AB=8,
∴点C坐标为(2,6),
∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段A′B′,
∴点C'的横坐标和纵坐标都变为C点的横坐标和纵坐标的一半,
∴点C'的坐标为(1,3).
故答案为:(1,3).
13.【解答】解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
14.【解答】解:∵BC⊥CA,MN⊥AN,
∴∠C=∠N=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴,
即,
∴MN=(m),
答:楼房MN的高度为m,
故答案为:.
15.【解答】解:∵正方形ABCD与正方形BEFG是以点O位似中心的位似图形,相似比为,EF=6,
∴BC∥EF,AB=BC=2,
∴△OBC∽△OEF,
∴=,即=,
解得,OB=3,
∴点C的坐标为(3,2),
故答案为:(3,2).
三.解答题(共4小题)
16.【解答】解:延长AD,如图所示.
∵∠1+∠BAC=180°,∠1+∠BDE=180°,
∴∠BAC=∠BDE.
又∵∠BAC=∠BAD+∠CAD,∠BDE=∠BAD+∠B,
∴∠B=∠CAD.
∵∠1=∠2,
∴△ABD∽△CAD,
∴=,即=,
∴AD=.
17.【解答】解:(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠BDE=180°﹣∠B﹣∠DEB,
∠CEF=180°﹣∠DEF﹣∠DEB,
∵∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF;
(2)∵点E是BC的中点,
∴BE=CE,
∵△BDE∽△CEF,
∴,
∴BE2=DBCF=6,
∴BE=CE=,
∵△BDE∽△CEF,
∴==,
故答案为:.
18.【解答】解:(1)如图1;
(2)如图2.
19.【解答】解:设DE=x,则BE=BD﹣x=6﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABP∽△CDP,即,
解得x=,
当时,△ABP∽△PDC,即,
整理得x2﹣6x+9=0,
解得x1=x2=3,
∴当DE为或3时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
一.选择题
1.在一幅地图上,用4cm表示哈尔滨工业大学到哈西客运站的地铁实际距离是8km,那么这幅地图的比例尺为( )
A.1:2
B.1:200
C.1:2000
D.1:200000
2.如图,在△ABC中,DE∥AB,且,则的值为( )
A.
B.
C.
D.
3.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm
B.32cm
C.48cm
D.52cm
4.若=,则的值为( )
A.
B.
C.
D.
5.如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,下列结论错误的是( )
A.AB2=BD?BC
B.AC2=DC?BC
C.AD2=BD?DC
D.BC2=AB?AC
6.如图,在平面直角坐标系中,已知△ABC与△DEF是位似图形,原点O是位似中心,位似比OA:OD=1:3,若AB=3,则DE的长为( )
A.5
B.6
C.9
D.12
7.在平面直角坐标系中,矩形OABC的顶点坐标分别是O(0,0),A(8,0),B(8,6),C(0,6).已知矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,且矩形OA1B1C1的面积等于矩形OABC面积的,则点B1的坐标为( )
A.(4,3)
B.(4,3)或(﹣4,﹣3)
C.(4,3)
D.(4,3)或(﹣4,﹣3)
8.下列各组线段中不能构成比例线段的是( )
A.a=3,b=6,c=2,d=4
B.a=1,b=,c=,d=
C.a=0.1,b=0.2,c=1,d=0.5
D.a=4,b=6,c=5,d=10
9.如图,在△ABC中,点D在BC上一点,下列条件中,能使△ABC与△DAC相似的是( )
A.∠BAD=∠C
B.∠BAC=∠BDA
C.AB2=BD?BC
D.AC2=CD?CB
10.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F
B.G
C.H
D.K
二.填空题
11.点C在线段AB上,AB=1cm,若AC2=ABBC,那么线段AC的长为
cm.,点B(8,0),点C在线段AB上,AC=2,若以原点O为位似中心,把线段AB缩小为原来的,得到线段A′B′,则点C的对应点C′坐标为
.
13.如图,有一个池塘,要测量池塘两端A、B的距离,可先在平地上取一点O,从点O不经过池塘可以直接到达点A和点B,连接AO并延长到点C,连接BO并延长到点D,使==3,测得CD=36m,则池塘两端AB的距离为
m.
14.如图,小明为了测量楼房MN的高,在离N点20m的A处放了一个平面镜,小明沿NA方向后退到C点,正好从镜子中看到楼顶M点.若AC=1.6m,小明的眼睛B点离地面的高度BC为1.5m,则楼高MN=
m.
15.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以点O位似中心的位似图形,且相似比为,两个正方形在点O的同侧,点A、B、E在x轴上,其余顶点在第一象限,若正方形BEFG的边长为6.则点C的坐标为
.
三.解答题
16.如图,点D在∠BAC的内部,∠1=∠2,∠1+∠BAC=180°.BD=1.5,CD=2,求AD的长.
17.如图,在△ACB中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,且BD=3,CF=2,则的值为
.
18.图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为单位1,三角形的顶点均在小正方形的顶点上,请按下列要求画:
(1)将图1中的三角形按2:1放大,在图1中画出放大后的三角形,使得画出的三角形的顶点均在小正方形的顶点上;
(2)在图2中根据给定的对称轴MN,画出已知三角形的轴对称图形.
19.如图,AB⊥BD,CD⊥BD,AB=9,CD=1,BD=6,点E在BD上移动,当以E,C,D为顶点的三角形与△ABE相似时,求DE的长.
参考答案与试题解析
一.选择题
1.【解答】解:8km=800000cm,
4:800000=1:200000.
所以这幅地图的比例尺为1:200000.
故选:D.
2.【解答】解:∵=,
∴=,
∵DE∥AB,
∴==,
故选:A.
3.【解答】解:设较大多边形与较小多边形的周长分别是m,n.则==.
因而n=m.
根据面积之和是80cm2.得到m+m=80.
解得:m=48cm.
故选:C.
4.【解答】解:设==t,则a=3t,b=2t,
所以==.
故选:C.
5.【解答】解:如图,∠ABD=∠CBA,∠ADB=∠CAB=90°,
由射影定理知,AB2=BDBC,AC2=DCBC,AD2=BDDC,故选项A、B、C不符合题意.
ACAB=BCAD,即BCAD=ABAC.只有当AD=BC时BC2=ABAC才能成立,故选项D符合题意.故
故选:D.
6.【解答】解:∵△ABC与△DEF是位似图形,
∴AB∥DE,
∴△OAB∽△ODE,
∴=,即=,
解得,DE=9,
故选:C.
7.【解答】解:∵矩形OA1B1C1O与矩形OABC位似,矩形OA1B1C1的面积等于矩形OABC面积的,
∴矩形OA1B1C1O与矩形OABC的位似比为1:,
∵矩形OA1B1C1O与矩形OABC位似,位似中心是原点O,点B的坐标为(8,6),
∴点B1的坐标为为(8×,6×)或(﹣8×,﹣6×),即(4,3)或(4,3),
故选:D.
8.【解答】解:A、6×2=3×4,能构成比例线段;
B、1×=×,能构成比例线段;
C、0.1×1=0.2×0.5,能构成比例线段;
D、4×10≠5×6,不能构成比例线段.
故选:D.
9.【解答】解:选项A、B、C的条件无法判断△ABC与△DAC相似.
正确答案是D.理由如下:
∵AC2=CDCB,
∴,
∵∠C=∠C,
∴△ABC∽△DAC(两边成比例夹角相等的两个三角形相似).
故选:D.
10.【解答】解:根据题意,
△DEM∽△ABC,AB=4,AC=6
DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
二.填空题(共5小题)
11.【解答】解:∵AC2=ABBC,
∴点C是线段AB的黄金分割点,AC>BC,
∴AC=AB=×1=(cm),
故答案为:.
12.【解答】解:∵点A(0,8),点B(8,0),点C在线段AB上,AC=2,
∴AB=8,
∴点C坐标为(2,6),
∵以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段A′B′,
∴点C'的横坐标和纵坐标都变为C点的横坐标和纵坐标的一半,
∴点C'的坐标为(1,3).
故答案为:(1,3).
13.【解答】解:∵==3,∠AOB=∠COD,
∴△AOB∽△COD,
∴===3,
∵CD=36m,
∴AB=3CD=108米.
故答案为:108.
14.【解答】解:∵BC⊥CA,MN⊥AN,
∴∠C=∠N=90°,
∵∠BAC=∠MAN,
∴△BCA∽△MNA.
∴,
即,
∴MN=(m),
答:楼房MN的高度为m,
故答案为:.
15.【解答】解:∵正方形ABCD与正方形BEFG是以点O位似中心的位似图形,相似比为,EF=6,
∴BC∥EF,AB=BC=2,
∴△OBC∽△OEF,
∴=,即=,
解得,OB=3,
∴点C的坐标为(3,2),
故答案为:(3,2).
三.解答题(共4小题)
16.【解答】解:延长AD,如图所示.
∵∠1+∠BAC=180°,∠1+∠BDE=180°,
∴∠BAC=∠BDE.
又∵∠BAC=∠BAD+∠CAD,∠BDE=∠BAD+∠B,
∴∠B=∠CAD.
∵∠1=∠2,
∴△ABD∽△CAD,
∴=,即=,
∴AD=.
17.【解答】解:(1)证明:∵AB=AC,
∴∠B=∠C,
∵∠BDE=180°﹣∠B﹣∠DEB,
∠CEF=180°﹣∠DEF﹣∠DEB,
∵∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF;
(2)∵点E是BC的中点,
∴BE=CE,
∵△BDE∽△CEF,
∴,
∴BE2=DBCF=6,
∴BE=CE=,
∵△BDE∽△CEF,
∴==,
故答案为:.
18.【解答】解:(1)如图1;
(2)如图2.
19.【解答】解:设DE=x,则BE=BD﹣x=6﹣x,
∵AB⊥BD于B,CD⊥BD于D,
∴∠B=∠D=90°,
∴当时,△ABP∽△CDP,即,
解得x=,
当时,△ABP∽△PDC,即,
整理得x2﹣6x+9=0,
解得x1=x2=3,
∴当DE为或3时,以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似.
